基于压电导波的钢梁损伤检测实验

王丹生， 张富成

(华中科技大学 土木工程与力学学院， 湖北 武汉 430074)

众所周知，现在土木工程项目都朝着大型化、复杂化和美观化方向发展，工程施工难度大，安全系数高，设计使用年限长。项目服役期间，结构会受到各种荷载的作用，不可避免地会出现各种损伤，而对损伤进行及时检测和处理，可提高结构的安全性、适用性和耐久性。如今，结构的损伤检测已成为土木工程的研究热点。

一般而言，结构损伤检测内容包括：判断损伤是否存在；若存在，确定损伤位置和判定损伤程度[1]。对结构进行损伤检测的方法有很多，随着材料科学的发展，近年来出现了很多无损检测技术，如阻抗法、导波法等[2]，其中导波法因其设备要求低，操作快捷方便，检测范围广、深度大、灵敏度高等优势被较多采用。国外学者采用压电陶瓷片(piezoelectric ceramic transducer，PZT)发射激励导波对板状结构进行损伤定位，并将该技术应用于检测机器等的损伤，取得较好的结果[3～5]。国内也对激励导波进行研究[6]，并选取合适的导波信号对混凝土[7～9]和钢梁[10]进行损伤检测，并用软件对钢梁损伤检测进行了数值模拟[11]。本文采用导波法对钢梁进行结构损伤检测实验研究。

1 Lamb波频散曲线和激励导波选取

本节首先介绍PZT片发射和接收导波信号的原理——压电效应，然后利用MATLAB求出本实验钢梁的群(相)速度频散曲线，并基于频散曲线，对本实验的激励导波信号进行选取。

1.1 PZT片的压电效应

压电效应是PZT片的一个重要智能特性，包括正逆两种压电效应。正压电效应是指PZT片受到纵向压(拉)力时，产生形变，内部极化，使上下表面产生电压，实现机械能向电能的转化，基于此效应可将PZT片用作接收器，如图1a所示；逆压电效应是指PZT片上下表面存在电压差时，其会产生机械变形，实现电能向机械能的转化，基于此效应可将PZT片用作激励器，如图1b所示。

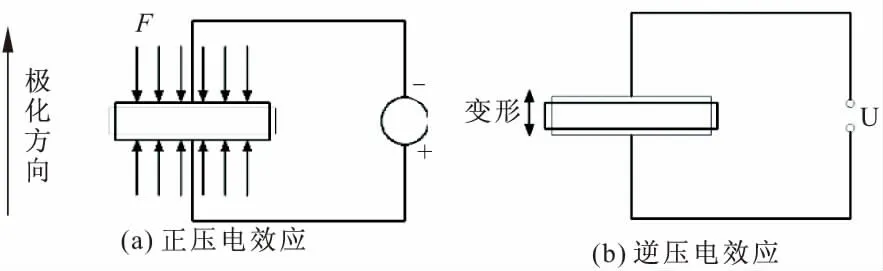
图1 压电效应示意

1.2 Lamb波频散曲线

Lamb波是指纵波和横波在传播过程中，由于上下边界限制，反射、叠加后形成的一种特殊应力波。激励导波在钢梁中是以Lamb波形式传播的。Lamb波在传播中，存在着对称模式(S型)和反对称模式(A型)。由于导波存在频散特性和多模态特性，导致一个频率段下会存在多种导波，因此需要根据其频散方程绘制出频散曲线，从而找出导波模态最少的频率段。

Lamb波频散方程[12]为：

(1)

(2)

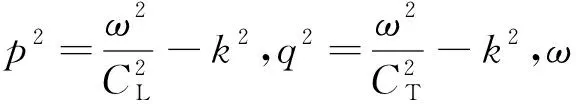
本实验钢梁的密度ρ=7.85 g/cm3，弹性模量E=2.06×105MPa，泊松比υ=0.3，因此可计算纵波波速CL和横波波速CT：

=5900 m/s

运用MATLAB求解出本实验钢梁中Lamb波的相速度频散曲线和群速度频散曲线，如图2所示。

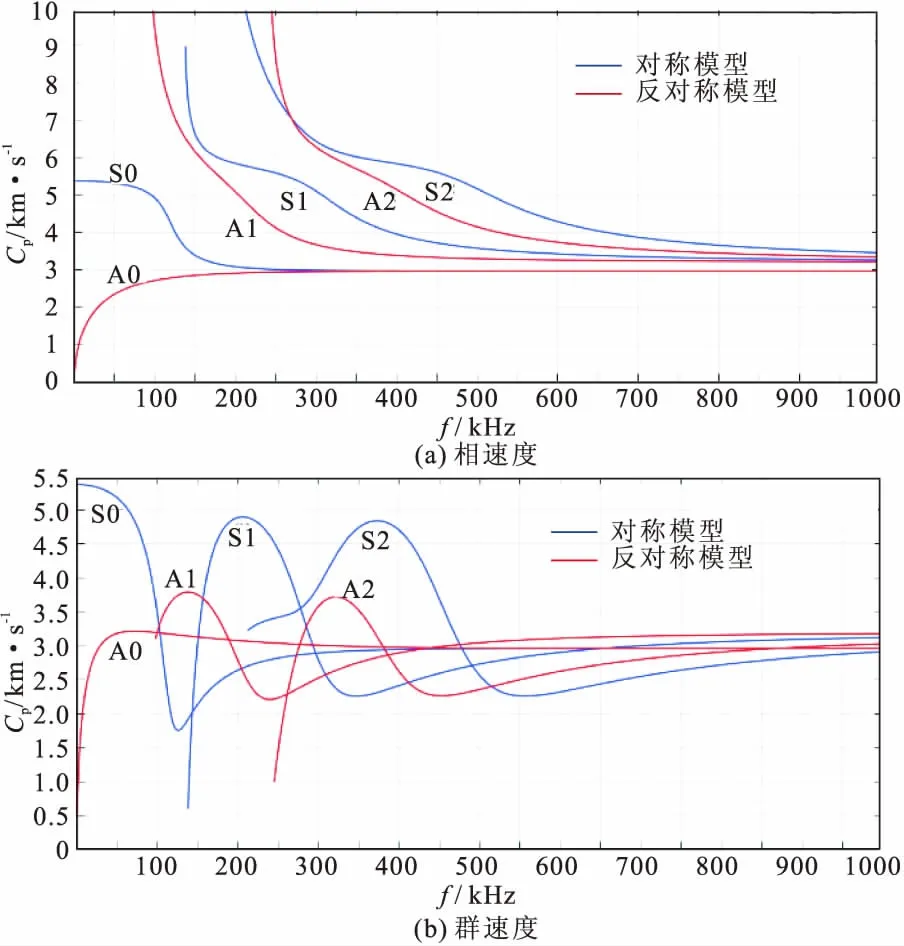
图2 钢梁前三阶模态频散曲线

通过图2频散曲线可得到以下信息：

(1)导波传播过程中，频散现象和多模态是共同存在的。即对于任何一条导波模态曲线，速度都随频率的变化而变化；对于同一频率段，又存在多个模态的导波。

(2)除了A0和S0两种模态外，其余高阶导波模态都存在下限值，即当导波频率低于此下限值时，此高阶模态导波不存在。

(3)观察频散曲线可得，频率为50 kHz时，导波模态只有A0和S0两种，且曲线变化平缓，适合作为激励信号中心频率。此时A0和S0导波的波速分别为3200 m/s和5200 m/s。

1.3 激励导波信号选取

选择合适的激励信号能够让实验结果更加明显。本实验激励信号从中心频率、窗函数和周期数目三方面进行选取。

(1)激励信号中心频率

参考群(相)速度的频散曲线，并使波速变化缓慢，本实验选择50 kHz作为激励导波的中心频率。

(2)窗函数选取

加窗处理后，激励信号的能量比未加窗时更加集中，可减少能量泄露，使得接收信号的效果更好。本文采用Hanning窗对激励信号调节，即激励信号y(t)为：

y(t)=Hanning(t)sin(2πft)

(3)

式中：Hanning(t)=0.5(1-cos(2πt/T))，T为窗宽，即总周期长度；f为频率。

(3)周期数目

周期的数目对激励信号识别损伤的敏感程度有很大影响。导波周期数目过多，信号携带能量多，识别损伤能力强，但本实验中，实验钢梁尺寸较小，容易掩盖损伤引起的微弱信号；导波周期数目少，信号频域宽，携带能量少，识别损伤的能力弱。本试验采用3.5周期的激励信号。

综上，本实验选用的激励信号如图3所示。

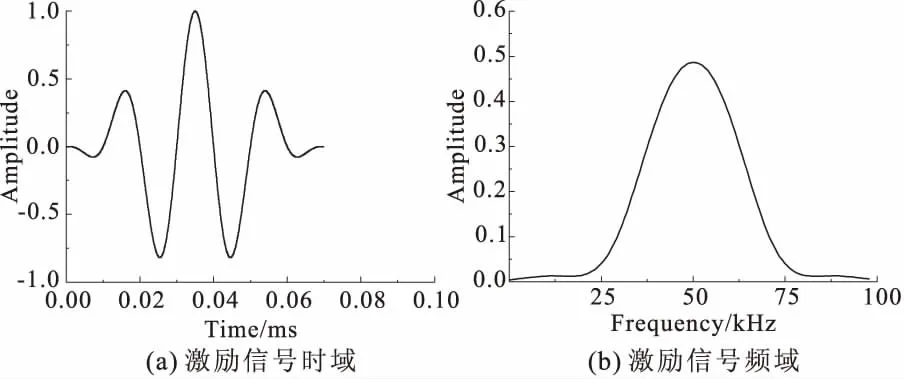
图3 3.5周期激励导波信号

2 钢梁损伤检测实验

本实验所用的钢梁尺寸为1000 mm×30 mm×20 mm，材质为Q235，密度ρ=7.85 g/cm3，弹性模量E=2.06×105MPa，泊松比μ=0.3。实验所用仪器为Agilent 33522B型号函数信号发生器和Agilent DSOX2014A型号示波器。本实验中将采用A0导波和S0导波分别对钢梁进行检测。

2.1 激励导波加载方式

前面已介绍，我们选用激励信号同时存在A0和S0两种导波。而采用双片激励可以产生单模态导波。双片激励是将两个PZT片对称放于钢梁上下表面，同时进行激励。其中，双片同相加载可抵消A0导波，只存留S0导波；双片反相加载与之相反；除此之外，双片加载会使向钢梁上下表面传播的导波叠加抵消，进一步减少导波的杂乱。连接示意图如图4所示。

图4 双片加载方式示意

2.2 实验流程图与测试图

实验流程图与测试图如图5，6所示。

图5 实验流程/mm

图6 实验测试图

我们分别采用PZT1，PZT3，PZT4作为接收器进行实验。其中，PZT1与PZT2(PZT5)，PZT3与PZT4之间的水平距离都为25 cm。

3 实验结果分析

3.1 钢梁损伤位置分析

(1)以PZT3为接收传感器

图7所示为损伤位置反射导波信号的示意图，可以知晓，第一个导波经过损伤反射后所传播距离为750 mm。

分别采用A0导波和S0导波进行测试，结果如图8所示。

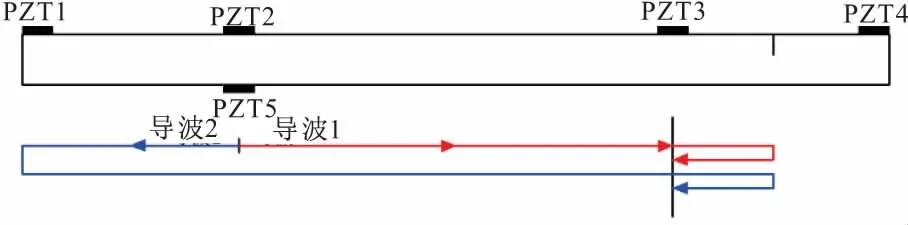
图7 损伤反射导波示意

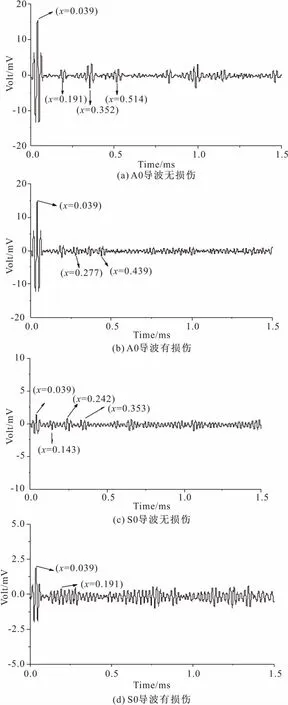
图8 PZT3为接收器接收信号测试结果

其中第一个接收信号波包为感应电信号产生，意义为激励信号的同步信号。接下来以此给出求解损伤位置的详细步骤，文章后续部分将不再给出。

根据图8a，8c计算A0和S0波速：

根据图8b，8d计算损伤反射信号传播距离d及误差Δd：

A0导波：

d=(0.277-0.039)×3214=765 mm

S0导波：

d=(0.191-0.039)×4837=735.2 mm

(2)以PZT1为接收传感器

图9所示为损伤位置反射导波示意图，A0导波和S0导波测试结果如图10所示。

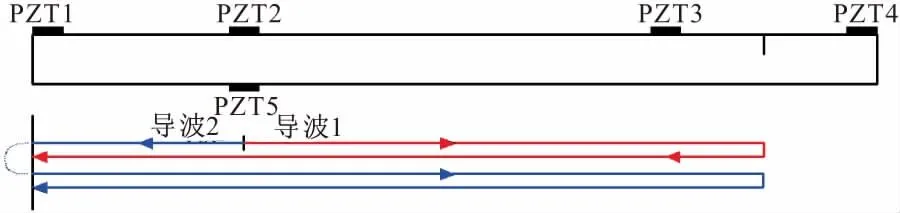
图9 损伤反射导波示意

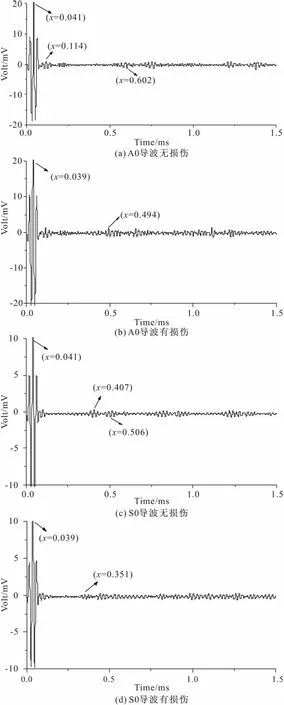
图10 PZT1为接收器接收信号测试结果

计算可得：A0导波：vA0=3272 m/s，d=1489 mm，Δd=0.75%。S0导波：vS0=4810 m/s，d=1500.72 mm，Δd=0.05%。

(3)以PZT4为接收传感器

损伤反射导波示意图见图11，导波测试结果见图12。

图11 损伤反射导波示意

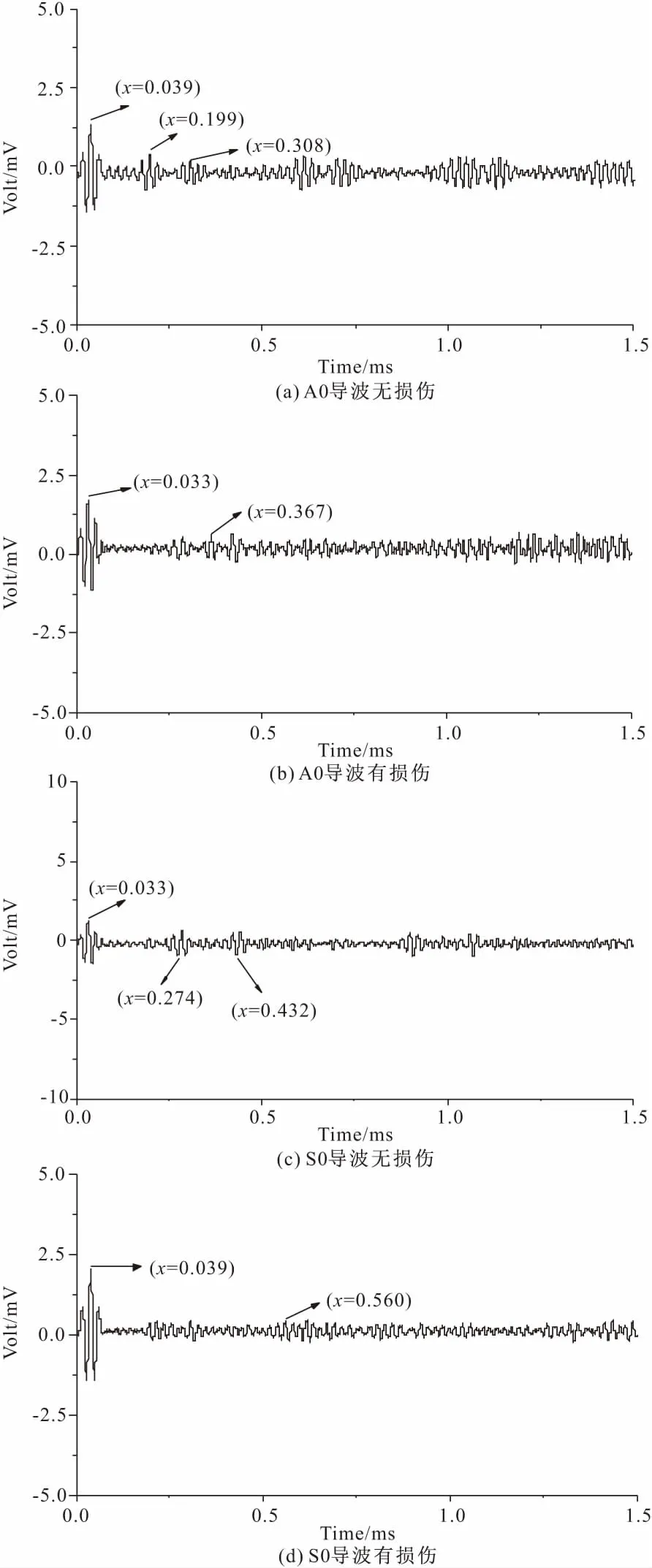
图12 PZT1为接收器接收信号测试结果

计算可得：A0导波：vA0=3122 m/s，d=1043 mm，Δd=4.30%。S0导波：vS0=4667 m/s，d=2432 mm，Δd=2.72%。

比较三种情况下的损伤定位误差，如表1。

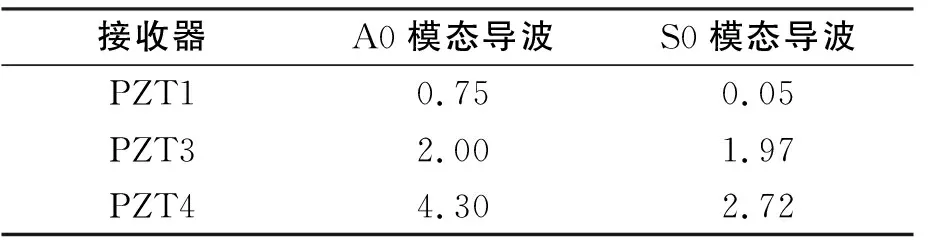
表1 A0和S0导波损伤定位误差 %

由表1可知：采用导波法对结构损伤进行定位的精度很高，都在5%以内；其中S0模态导波比A0模态导波定位精度高；且将激励器和接收器放在损伤同一侧可以提高损伤定位精度。

3.2 钢梁损伤程度分析

由于A0模态导波振幅大，波包间隔长，容易显示出损伤信息，因此本实验中只采用A0导波进行分析，比较结构在无损伤，5，10，15 mm四种程度下的接收信号中，端面反射导波幅值和损伤反射导波幅值与损伤程度之间的关系。

(1)端面反射导波幅值(以PZT3为接收器)

图13所示为以PZT3为接收传感器时，A0模态导波在无损伤，5，10，15 mm损伤状态下的接收信号，并且在图中已标出端面反射导波幅值。

图13 不同损伤程度下接收信号测试结果

由图13可知，激励导波遇到损伤时会发生反射和透射，且随着损伤程度的加大，反射值增加，透射值减少，表现为接收信号中，随着损伤程度的增加，损伤所反射的导波幅值增大，钢梁端面反射导波幅值减小。图14为损伤程度与钢梁端面反射幅值关系图。

图14 损伤程度与端部反射导波幅值关系

由此可见，随着损伤程度加大，端面反射幅值不断减小，且两者之间呈线性关系，且线性相关性很强。

(2)损伤反射导波幅值(以PZT1为接收器)

图所15示为以PZT1为接收传感器时，A0模态导波在无损伤，5，10，15 mm损伤状态下的接收信号，并且在图中已标出损伤反射导波幅值。

图15 不同损伤程度下接收信号测试结果

由图15可知，激励导波遇到损伤时，会发生反射，且随着损伤程度的增加，损伤所反射的导波幅值增大。图16为损伤程度与钢梁端面反射幅值关系。

由图16可知，随着损伤程度加大，损伤反射幅值不断增大，且两者之间呈线性关系，且线性相关性很强。

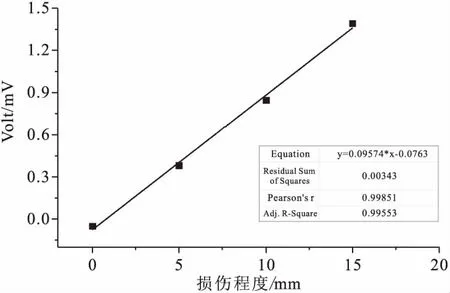
图16 损伤程度与损伤反射导波幅值关系

综上，基于导波法可以对结构的损伤程度进行判定。由于损伤的出现，激励导波在损伤位置处会出现反射和透射，损伤程度的大小决定着发射和透射的能量多少，且前者和后者之间具有很好的线性相关性，鉴于此，可实现损伤程度的定量判定，即可以通过将检测到的端面反射导波幅值或损伤反射导波幅值在已知的损伤程度曲线中进行插值，从而获得损伤程度。

3.3 微小质量增加敏感性检测

本实验用于检测导波法对结构质量出现微小变化时的敏感性，通过在钢梁上放置质量为200 g的砝码(图17)，检测接收信号是否出现变化，即是否有新的波包出现或者激励导波是否出现峰值上的显著增减。本实验中采用A0激励导波。

图17 砝码位置示意/mm

PZT1，PZT3，PZT4在无砝码和有砝码时的接收信号对比如图18所示。

图18 砝码放置前后接收信号对比

由图18可知，PZT1，PZT3，PZT4的接收信号在砝码放置前后，并没有明显波包的增减，曲线基本重合，说明：当砝码放在如图所示的位置时，所有的接收传感器都无法测出此砝码对实验钢梁的影响。

(2)砝码位置改变，PZT接收传感器固定。

砝码位置的改变如图19所示，以PZT3为接收传感器。

图19 砝码位置变化示意/mm

四个位置时的接收信号对比如图20所示。

图20 砝码不同位置时接收信号对比

如图20所示，采用相同的检测方式(激励器和传感器)，砝码分别放于四个位置时，接收信号基本重合，没有变化，说明砝码的位置依然不能引起接收信号的变化。

综上可得：钢梁上微小的质量变化不能引起接收信号的变化，说明导波法对微小质量增加不敏感，侧面说明导波法对微小损伤的识别精度较低。

4 结 论

本文主要对导波法用于钢梁的损伤检测进行了实验研究。采用三个接收传感器，对比了A0和S0两种模态的激励导波信号，对损伤位置、损伤程度以及导波法对微小质量增加敏感性等问题进行了研究，得到以下结论：

(1)通过频散曲线可知，导波激励频率在50 kHz处导波模态只有A0和S0两种，且波速变化平缓，频散特性影响较小，适合作为激励信号中心频率；且通过双片激励可产生单模态导波；

(2)切割损伤后，激励导波传播到损伤位置处时，会发生反射和透射现象，具体表现为接收信号上出现导波包增多、端面反射导波包幅值下降现象。

(3)A0和S0模态导波都可对损伤位置进行定位，且精度都在5%以下，其中S0导波的定位精度比A0导波精度高，对比还可发现，将激励器和传感器放在损伤的同一侧可提高对损伤定位的精度。

(4)通过对不同损伤程度的导波接收信号分析可知，随着损伤程度的不断加深，由损伤反射的导波包幅值不断增加，端面反射的导波幅值不断减小，而且损伤程度与这两者导波幅值之间存在线性关系，且线性相关性很强；

(5)通过对200 g砝码粘贴钢梁实验可知，导波法对微小质量增加这一变化的敏感性很低，无论粘贴于钢梁上任何位置，也无论采用任何位置的PZT接收器进行实验，粘贴砝码前后的接收信号基本重合无变化。