培养直觉思维，学会“跟着感觉走”

曹彩华

[摘 要] 在数学学习过程中，教师强调的“感觉”实质上是一种直觉思维，而直觉思维一定程度上能反映学生的创造力. 现如今，社会的快速发展对我们的创新思维能力要求较高，因此教育工作者要通过教学活动培养学生的直觉思维，促进学生全面发展.

[关键词] 初中教学；直觉思维；人教版

数学强调的是逻辑思维，要求学生对问题进行理性思考. 但是，在听取了一节习题公开课过后，笔者发现，在解题过程中，学生既需要严谨的数学思维，又需要一定的直觉思维，即不经过严格的逻辑思维就能理解问题、给出问题答案的能力，这样能极大地简化选择题、填空题的解答过程，同时能为证明题、计算题等题型提供思路. 下面笔者结合教学实例进行阐述.

巧用对称性

在现实世界中，很多事物的美都体现在其本身的对称性上. 数学是生活的抽象，数学中的菱形、圆、抛物线等都是高度对称的图形. 在解决数学问题的过程中，学生常常会遇到看似不规则的、不对称的图形，但通过分割、补全、折叠等方式能使图形出现对称的部分，便于寻找其中的几何关系或数量关系，进而应用各种定理或性质解决问题. 下面进行举例说明.

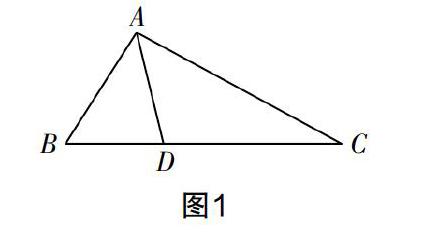
案例1 如图1，在△ABC中，AD是∠BAC的平分线，且AC=AB+BD，试证明∠B=2∠C.

师：同学们，拿到这道题，大家认为哪一个条件是关键？

生1：AD是∠BAC的平分线.

师：既然题目中有一个角的平分线是已知条件，那大家会怎么使用呢？

生2：可以构造全等三角形.

师：具体怎么做呢？

生3：以AD为对称轴折叠三角形ABC，因为∠BAD与∠DAC相等，所以边AB在折叠后会落在边AC上，我们假设折叠后的点B落在点E处（如图2），依据折叠的性质可得△BAD≌△EAD. 再结合“AC=AB+BD”这一条件可以證明∠B=∠C+∠EDC=2∠C.

评析 在这道题的证明过程中，学生利用角的轴对称性进行直观体会. 当然，在解题过程中，学生要适当绘制辅助线，便于思考. 图形的对称虽然不是一个直接考点，但在很多几何题型中都会用到，具有较强的实用性，因此教师要引导学生深入感受这一思想方法，做到灵活运用.

学会数形结合

代数问题具有较强的抽象性，学生思考起来比较困难. 在处理一些代数问题时，学生可以借鉴几何图形，利用几何图形的性质来描述其中的数量关系，使思维过程更直观，这样的思维方法更符合中学生的认知.

案例2 已知正数m，n满足m+n=2，试求+的最小值.

师：这道题是求最小值，最值问题的常规思路有哪些？

生1：函数.

师：那同学们觉得这道题构造成关于m或关于n的函数之后，该怎么求最小值呢？

生2：这个函数好复杂啊.

师：同学们再观察一下“+”这个条件，什么样的情况下会出现这样的根式？

生3：想不起来了.

师：我再提醒一下，“”可以看成“”，“”可以看成“.

生4：直角三角形求斜边长度！

师：很好！那这道题我们不从代数的角度去思考，我们借助直角三角形，将这道题转化为两个直角三角形斜边之和. 那大家觉得该怎样设置这两个三角形呢？

生5：可以在长度为2的线段上设置动点，分别表示m与n.

师：来，把你构想的图形画到黑板上.

（生5于是在黑板上画出了图3，即AE=EF=2，BF=1，∠AEF=∠BFE=90°）

师：很好，这道题基本可以解决了. 哪位同学来说说答案是多少？

生6：根据“两点之间，线段最短”，即A，C，B三点共线时值最小，可得最小值为.

评析在利用数形结合方法解决代数问题时，关键是明确几何化的方法以及绘制怎样的几何图形. 因此，这种方法的难点就是学生要对几何问题以及代数问题有深刻的认识，能快速反应，将两者进行联系与转化. 在学习与使用这种直观方法的过程中，学生会渐渐明白同一个知识内容会有不同的表现形式，知识内容的学习不能固化，更不能僵化，要做到灵活变通，追本溯源，掌握核心.

类比思想

在解决实际数学问题的过程中，类比是一种直觉思维应用形式，这种思想方法需要寻找两个对象的相似点，以此为基础进行处理. 在解决问题时，学生如果能通过一个数学对象发现与之相类似的另一个对象，就能使用类比推理的方法进行解决.

案例3 已知线段AB上一共存在n个点（含端点A，B），那么这条线段上共有多少条线段？

师：在解决这个问题前，同学们先思考一下线段是由什么决定的.

生1：两个端点.

师：两个端点分前后顺序吗？

生2：线段与端点的前后顺序无关.

师：没错. 明确了这两点之后，我们先试着从一个端点出发. 哪位同学回答一下线段AB上任意一点构成的线段有多少条？

生3：（n-1）条.

师：那么所有的点构成了多少条线段？

生3：n×（n-1）条.

师：其他同学有不同的意见吗？

生4：这样算的话，每两个端点因为前后顺序不一样而被计算了两次，所以答案应该是条.

师：很好. 那接下来对这道题进行改编——如果从一个定点引出n条射线，一共能组成多少个角（不包含大于180°的角）？

生5：跟线段一样，角只与两条边有关，且无序，所以一共可以组成个角.

评析 类比终究只是基于相似性的处理方法，所得到的结论不一定是正确的，并且结论还需要进一步验证才能成立. 尽管如此，这种处理方法对于提升学生的直觉思维以及创造力来说具有较大的意义. 因此，在实际的教学活动环节，教师需要运用这种方法讲授新知识，加强新、旧知识点之间的联系，经常启发学生，不断提升学生的直觉思维能力.

合理猜想

案例4 如图4，在等边三角形ABC中，点E在AC上，且AE=CD，BQ⊥AD于点Q，BE交AD于点P，则BP-2PQ的值为（ ）

A. 1B. -1C. 0D. 无法确定

师：同学们，在做选择题和填空题时，因为不需要书写过程，因此大家可以根据已知信息大胆假设，根据假设找条件，去验证自己的假设是否正确，这样能给大家节省不少时间. 这是一种有效的应试技巧. 在这道题中，有“BQ⊥AD”这一条件，要求解的是一个二倍关系，同时选项中有“0”这样一个特殊值，大家会进行怎样的假设？

生1：∠PBQ=30°，BP=2PQ.

师：顺着解题思路确实很容易有这样的假设，看图也比较符合，那如果这是一道证明题，严格证明的思路是什么呢？

生2：根据“SAS”可以证明△ABE≌△CAD，于是有∠ABE=∠CAD. 而△ABC是等边三角形，所以∠BAC=60°. 所以∠BPQ=∠ABP+∠BAP=∠CAD+∠BAP=∠BAC=60°. 又BQ⊥AD，所以∠PBQ=30°. 所以BP=2PQ，即BP-2PQ=0.

评析 解决数学问题时，适时地进行猜想与假设也是一种有效的直觉思维，能简化学生的思维过程，提升学生的创造力. 因此，在日常的课堂教学以及练习中，教师要选择适当的练习题，引导学生进行猜想与假设，进而提高学生的直觉思维能力. 比如，在选择题的解答过程中，可以“由果索因”，以已知选项为突破口，合理地进行假设，省略思维与解题过程.

综上所述，在初中数学的学习过程中，提升学生的直觉思维能力也是教学重点，是课程改革的一大关键. 因此，广大教师需要转变固有的教学观念，既要讲授好知识内容，又要加强学生的直觉思维，引导学生大胆联想，勇于质疑，科学验证，继而培养与提升学生的直觉思维能力.