基于EEMD分解和多分类支持向量机的飞行器舵面系统故障诊断

肖 东， 江 驹， 余朝军， 周 俊

(南京航空航天大学，南京 210016)

0 引言

飞机舵面系统是飞行器正常工作的重要部件，频繁的控制任务使舵面的执行机构成为最容易发生故障的部分，执行机构性能的改变直接影响飞行控制策略以及控制指令，影响操纵者的分析和决策，因此，对舵面系统的故障进行及时的检测和诊断就显得非常重要。舵面执行机构常见的故障类型有结构性损伤、飞车饱和、卡死、损伤(部分失效)、松浮、反向、噪声干扰等[1]，其发生故障后，会给系统的输出带来附加扰动和不确定性，导致非平稳输出信号在时域和频域上发生变化[2]。

由于数学模型难以完全贴近实际中的舵面执行机构，一般利用系统输出/振动信号等进行故障类型的识别，国内外学者提出基于时频分析的特征提取和模式识别等相结合的智能故障诊断方法[3-4]。文献[5]利用D-S算法和神经网络信息融合技术对输出信息进行融合，用于舵面的损伤状态检测，但该方法利用模式匹配只能分析相同模式的损伤程度，对没有经过学习训练的样本不具有很好的识别能力。文献[6]利用小波包分析和支持向量机相结合的方法，对舵面执行机构的结构性损伤进行特征提取和识别诊断，但是其利用小波包分析提取到的不同频段的能量特征明显集中在高频噪声区，而且小波包分析更加适合于频率信息丰富的振动信号，对低频输出信号的区分并不十分明显，尤其是难以识别执行机构的正常状态和损伤状态。

经验模态分解根据信号本身自适应地选择滤波频带以及不同频段的分辨率，克服了传统包络分析依赖预处理的问题，而且该方法适用于非平稳信号[7]。为此，本文采用改进的经验模态分解-集合经验模态分解方法将舵面系统的信号分解成多阶固有模态函数，然后计算包含主要故障信息的各阶分量的能量并将其作为特征向量，最后利用分解到的特征信息训练基于后验概率的多分类支持向量机，进而判定舵面执行机构的故障类型。

1 舵面信号的EEMD分解

与小波分解算法不同，经验模态分解(Empirical Mode Decomposition,EMD)基于信号的局部特征时间尺度，把复杂的信号函数分解为有限的固有模态函数，进而导出有意义的希尔伯特变换时频谱。该算法克服了小波包分解对小波基函数的依赖，提高了对时频的分辨率，是一种自适应的数据分解方法，其算法描述见文献[8-9]。

经验模态分解作为一种自适应的信号分析方法已被广泛应用，但是该方法在信号分解过程中容易产生虚假分量并产生低频分量混叠。为抑制这些问题，文献[10]提出集合经验模态分解方法(Ensemble Empirical Mode Decomposition， EEMD)，该方法本质是对叠加了高斯白噪声的被分析信号进行多次EMD分解，利用高斯白噪声频率均匀分布的统计特性使被分析信号在不同尺度上具有连续性，从而降低各IMF分量的模式混叠程度。根据零均值高斯白噪声的特性，通过若干组IMF 总体平均使加入的高斯白噪声互相抵消，还原被分析信号。

EEMD算法的具体步骤如下所述。

1) 对系统输出信号x进行降噪预处理，然后将其标准化。

(1)

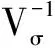
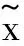
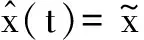
(2)

4) 重复步骤2)，3)直到剩余分量不能再次分解。

这样，舵面输出信号经过多次分解以后可得

(3)

式中：ci(t)为每次分解出的本征模态函数；rn(t)为分解后的残余函数，代表了信号的整体变化趋势。

2 多分类支持向量机的设计

支持向量机方法由VAPNIK等提出，最初应用于二分类问题，算法原理见文献[11]。由于该分类方法在处理小样本、非线性问题中具有良好的泛化能力而逐渐被应用于故障诊断领域。但是由于故障类型的多样化，因此需要将二分类支持向量机扩展到多分类。对于多分类问题，较为实用的方案是将多分类问题转化为多个二分类问题进行解决，这种方案包括一对一、一对多、层次多分类法等。前两种方法效率较高，但是存在不可识别域；层次法难以解决样本不均衡导致的最优分类面的偏移问题[12]。因此，本文在后验概率的基础上采用多个一对一分类器构建多分类支持向量机。

本文选取舵面执行机构常见的5种典型输出，即正常、卡死、松浮、损伤以及反向为例进行诊断研究。首先需要建立10个一对一的二分类支持向量机(SVM1～SVM10)，对于单个二分类器，假设这两种故障类别的标签为y=±1，其对应的特征向量x=[x1，x2，…，xn]，那么其后验概率可表示为

p(y|x)=(p(y)p(x|y))/(p(x))

(4)

式中：p(y)为故障类型对应的先验概率，由历史样本分析获得；p(y|x)为故障类型对应的后验概率，反映了历史样本数据对测试数据的影响。

对于多个分类器的问题，则需要建立多分类器的后验概率组合。假定测试样本x属于第i类，那么其隶属的后验概率为

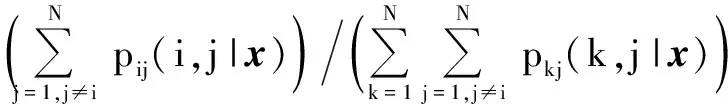
(5)

式中，pij(i,j|x)为二分类器中x隶属于第i类的后验概率。

由于

(6)

因此式(6)可变为

(7)

最后利用10个二分类器构建多分类机，然后再利用多分类机输出的后验概率进行组合，得到基于后验概率的多分类机诊断模型，如图1所示。该多分类机在样本识别过程中不存在诊断盲区问题，而且避免了训练样本的不对称问题，结构简单、运行效率较高。

图1 基于后验概率的多分类支持向量机模型

3 舵面执行机构模型及故障诊断仿真

无人机舵面的输入信号由控制律提供，输出信号由其末端的线位移传感器采集。实际中，舵面控制系统是一个高阶非线性环节，其数学模型可以简化为二阶环节，传递函数为[13]

(8)

式中：δL是舵面的偏转角；U是系统输入的控制信号。

飞机的舵面系统主要包括左右副翼、升降舵和方向舵系统。考虑到方向舵的结构具有非对称性，其故障对无人机横向运动的影响明显，因此本文选择以方向舵为例进行仿真分析。

首先建立无人机仿真模型并多次采集其在某高度平飞状态下的方向舵在正常和4种故障模式下的输出信号，然后利用第1章中的EEMD算法对信号数据进行分解，得到一系列对应的IMF分量。图2显示了方向舵系统在正常和几种典型故障模式下的数据表现形式。

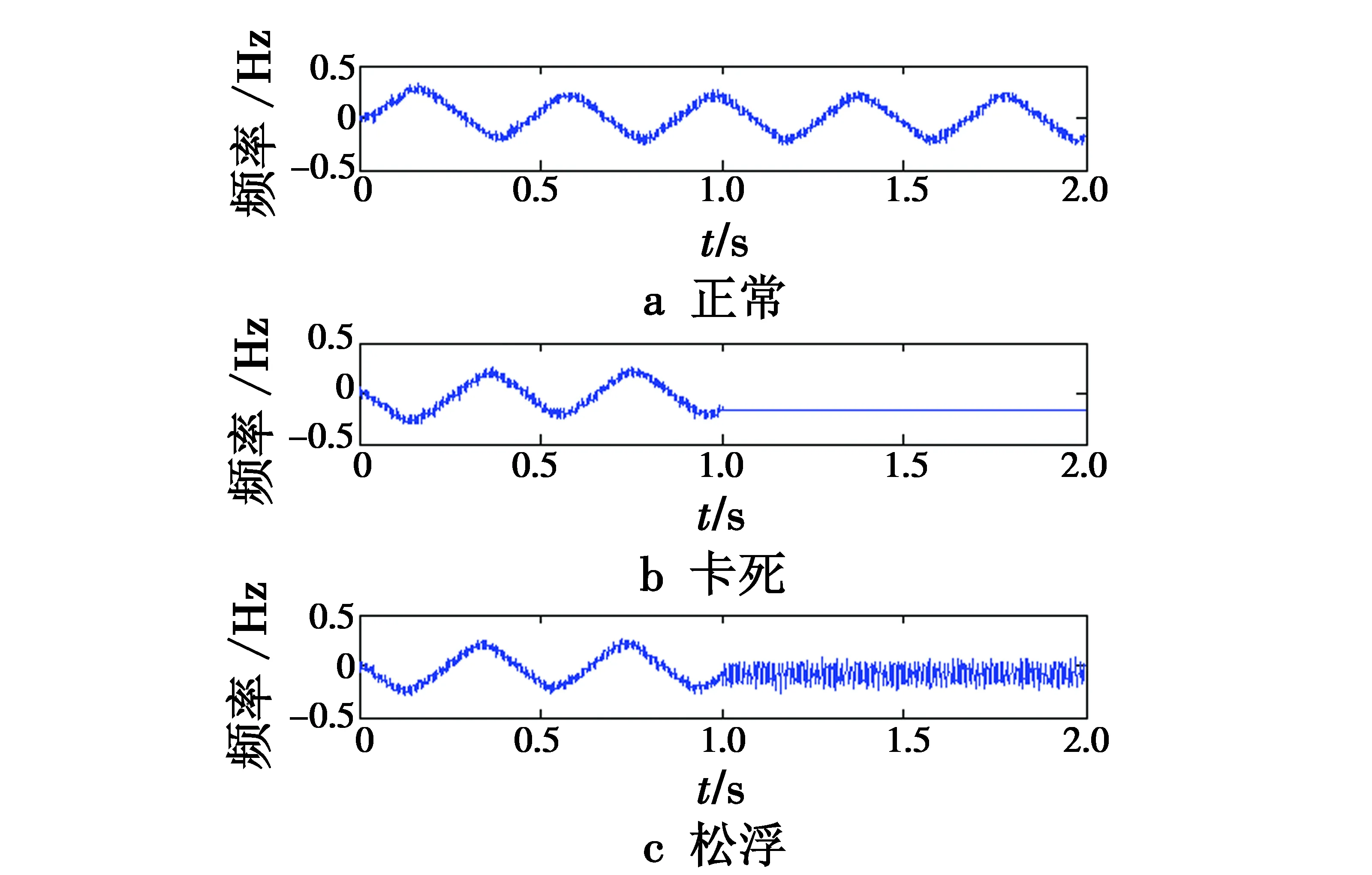
图2 方向舵输出信号表现形式Fig.2 Typical output signals of rudder

小波包分解法利用不同频段的小波包系数对应的能量占比对系统输出信号进行特征提取，如图3所示。可以看出，分解即使很细，某些能量特征仍不明显，而且故障类型间区分度不大，比如正常状态与松浮状态，卡死状态与损伤状态。

图3 小波包分解能量特征分布图

EEMD方法根据信号本身的特点自适应地将不同频段内的固有成分分解到不同的IMF中之后，直接计算各模态函数对应信号的分立能量作为特征向量，用于故障分类，即

(9)

T=[Es1，Es2，…，Esk-1，Esk]

(10)

式中：n为分解后各阶IMF分量中的信号点数；k为IMF分量的数目。

图4和图5分别给出了方向舵在正常状态和损伤50%状态下的EEMD分解结果的前5个本征模态函数。由图可知，原信号中的噪声和突变点都在IMF分量有明显的显示，而且方向舵发生损伤前后的幅频分量在IMF4和IMF5得到了区分，显示出该算法抑制了频率混叠现象。

图4 舵面正常状态下EEMD分解结果Fig.4 EEMD decomposition of normal rudder

图5 舵面损伤状态下EEMD分解结果Fig.5 EEMD decomposition of damaged rudder

然后利用IMF计算对应的分立能量作为特征向量，图6给出了方向舵系统5种状态下的故障特征向量分布，从分布图可以看出，几种状态的特征相对明显，正常状态、松浮状态以及卡死状态等也表现出可区分性。

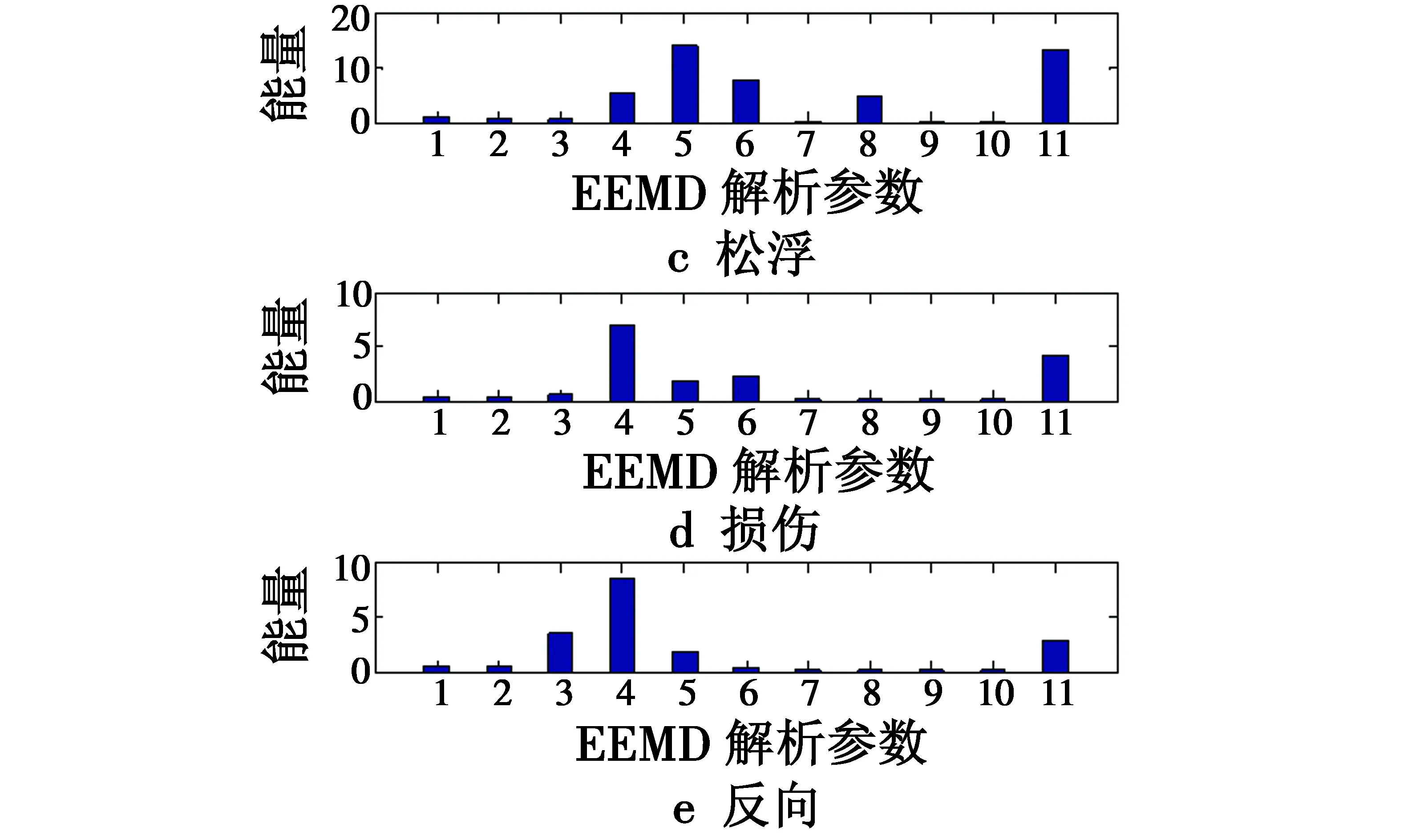
图6 舵面系统典型状态下的故障特征分布Fig.6 Fault characteristics distribution of the rudder system under typical conditions

进行多次仿真采样，最终得到无人机方向舵系统在5种状态下的数据各80组，对信号进行小波滤波以后，按照第1章中的步骤提取特征向量，然后随机选取60组样本数据对建立的多分类支持向量机进行训练，并将余下的作为测试样本输入分类机模型进行故障模式识别。

针对核函数直接影响二分类支持向量机的分类效果，本文选择RBF核函数

k(xi，xj)=exp(-‖xi-x‖2/2σ2)

(11)

并利用10折交叉验证算法对所有SVM分类器进行参数寻优，保证最终的分类效果。作为对比，这里同时使用基于EMD分解的多分类算法进行仿真，诊断结果如表1所示，本文算法能够较好地区分出方向舵系统的状态，验证了算法的有效性。

表1 不同多分类模型的诊断效果

由表1可以看出，EMD多分类方法的分类效果稍差，这与信号分解出的IMF分量数目不同和模态混叠现象有直接的关系，而利用EEMD多分类法对方向舵信号的分解较为彻底，因而在故障多分类中具有较好的识别效果。

为比较小波包分解-多分类算法和EEMD-多分类分解算法对分类性能的影响，分别随机取不同数量的信号样本进行特征提取和多分类机的训练，然后对剩余测试样本进行识别分类；同时为说明EEMD-多分类算法相比人工神经网络更加适应小样本分类情况，利用两种算法对同种方法提取的不同样本组的特征向量进行测试识别。其中神经网络选用三层神经网络，其输入节点数为11，隐含层节点数为18，输出节点数为5，如[1,0,0,0,0]表示正常状态，[0,0,1,0,0]表示松浮故障。最终通过对比仿真得到以下分类结果，如表2所示。

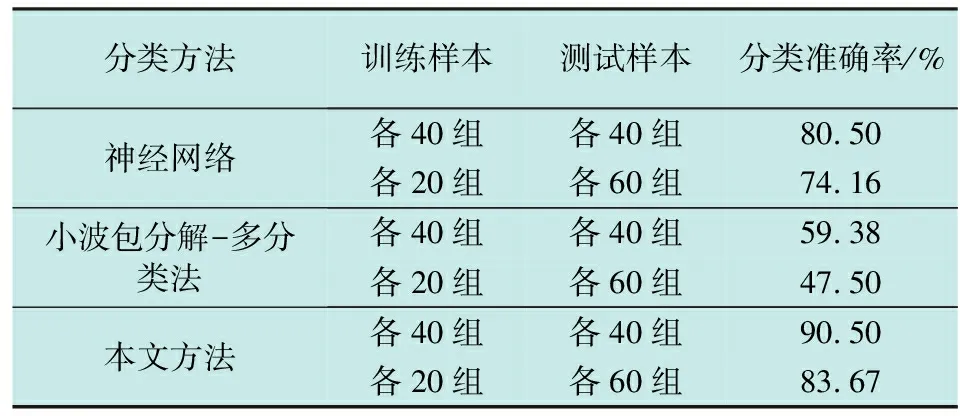
表2 不同诊断算法下的分类性能比较

结果表明，由于输出信号的频谱范围有限，小波包分解-多分类算法不能有效地进行方向舵信号的特征提取，因此对故障类型的识别效果较差；而利用EEMD分解算法进行特征提取，再使用神经网络算法对测试样本的故障类别具有较高的平均识别率。虽然当训练样本不足时，故障分类效果有所降低，但是随着样本数目的不断增加，故障识别率也逐渐改善，这也从侧面验证了EEMD分解法对特征提取的有效性。

4 结束语

本文提出基于EEMD算法的特征提取和多分类支持向量机的飞机舵面故障诊断方法，利用EEMD算法自适应地将信号分解为具有真实意义的本征模态函数，消除了小波包分解对频域划分的不确定性问题，避免了EMD分解的模态混频现象；利用基于后验概率的支持向量机分类方法，避免了标准支持向量机绝对的划分，更接近于实际。对舵面故障的5种典型工况的识别可以看出，该方法能够不依赖精确的数学模型，仅根据系统的输出信号分析出系统故障类型并达到较高的准确率。由于无人机舵面系统包含执行机构和传感器两部分，其真实输出信号会受到两者的综合作用，因此对于耦合信号的故障诊断将是下一阶段的研究内容。