基于卷积神经网络SAR图像仿真参数预测

银玉琳, 黄 山,b

(四川大学,a.电气信息学院; b.计算机学院，成都 610065)

0 引言

成像雷达遥感一般指合成孔径雷达(SAR)遥感，其显著特点是主动发射电磁波，具有不依赖太阳光照及气候条件的全天时、全天候对地观测能力，并对云雾、小雨、植被及干燥地物有一定的穿透性。此外，通过调节最佳观测视角，其成像的立体效应可以有效地探测目标地物的空间形态，增强地形地貌信息。这些独特的优势使得雷达遥感相对光学遥感，尤其对于传统光学传感器成像困难的地区有着特别的意义[1]。目前我国SAR系统技术已经得到长足的发展，相关技术已经处于世界先进水平，未来几年随着我国多型新体制SAR卫星的发射，我国SAR技术将跻身国际领先水平。我国SAR数据的获取能力正在不断增强，每天都在获得大量观测数据，然而，目前SAR数据的应用能力与SAR数据获取能力是不相匹配的。由于电磁散射的复杂及不直观性，以及目标电磁散射效应随角度、频率、极化等因素的多变性，目前人们对于SAR目标特性的掌握还比较有限，成为制约SAR应用技术发展的瓶颈。为了提升SAR应用的基础支撑能力，各方均认为应该建设完备的SAR目标特性库，目前，目标特性库的建设主要有两种方法。一种方法是基于实测样本，该方法虽然能够保证样本的真实有效性，但其缺陷在于实测样本的离散和不完备性。虽然我国已有了多颗SAR卫星，并且国内也有多家单位拥有机载SAR系统，但受到轨道和空域的限制，以及电磁散射随角度、频率等的时变性，对于目标(尤其是国外非合作目标)而言，所获观测样本在观测角度、方向、频率、极化、分辨率等方面都是离散和非常不完备的。另外，对于非合作目标而言，其类型、状态等真值很难获取。因此，在现阶段以及将来很长一段时间内，如完全依赖实测样本，建立大数据意义上的SAR目标特性库，仍然面临极大的困难。另一种方法是基于电磁建模仿真。国外对SAR图像仿真的研究起步较早，美国、日本等早在20世纪70年代就已经开始对SAR图像进行仿真研究，研制的雷达图像仿真系统有ARKANSAS,SARAS等[2]。结合实测SAR图像，仿真SAR图像可为SAR图像解译包括人工解译和自动解译以及目标识别提供丰富的数据资源，建立目标各种操作条件下的模板数据库[3]。这类方法得到的仿真图像能较真实地反映SAR图像特征，但图像准确性依赖于地物的仿真参数，而仿真参数通常只能由实验得到[4]。

近年来，随着深度学习的发展以及卷积神经网络(CNN)的兴起，图像处理技术得到了极大的进步。CNN在很多图像识别数据集中取得了很好的成绩，20世纪80年代末，美国纽约大学教授LECUN[5]将CNN用于手写数字识别，作为美国银行识别票据的工具。2012年，加拿大多伦多大学深度学习的领军人物HINTON教授[6]利用深层的CNN在大尺度图像识别数据集Image Net上取得了较好成绩。美国Facebook网站[7]也利用深层CNN在人脸识别上取得97.25%的识别率。国内创业团队Face++[8]利用Pyramid CNNs在人脸识别公共数据 LFW上获得第一。传统的图像分类方法，如贝叶斯分类器[9]、支持向量机[10]等都需要进行复杂特征提取选择。神经网络已经在分类[11]、检测[12]、分割[13]、回归[14]等领域取得了较好的应用效果，而CNN直接以图像的像素值作为输入，避免了传统分类算法中的数据预处理过程。为了得到最佳的电磁建模仿真参数，本文提出一种基于CNN的SAR图像仿真参数回归方法来实现对SAR图像仿真参数的预测。

1 CNN回归模型构建

CNN是在多层神经网络的基础上发展起来的针对图像分类和识别而特别设计的一种深度学习方法。卷积网络是为识别二维形状而特殊设计的一种多层感知器，这种网络结构对平移、比例缩放、倾斜或者其他形式的变形具有高度不变性。本文设计了一种用于SAR图像仿真参数预测的CNN结构，如图1所示，该网络由11层神经网络构成，其中包括输入层、4层卷积层、4层下采样层、1层全连接层和1层输出层。

图1 CNN模型结构Fig.1 CNN model structure

1.1 卷积层

根据生物视觉细胞局部感受野的理解，卷积层通过局部连接和权值共享的方法，提取一些初级视觉特征。局部连接指卷积层上的每个神经元与前一层特征图中固定区域的神经元建立连接。权值共享指同一特征图中的神经元用一组相同的连接强度与前一层局部连接，大大减少了网络训练的参数。如图2所示，在一个卷积层，输入层的特征图被一个卷积核进行卷积，然后通过一个激活函数，就可以得到输出特征图。

图2 卷积操作Fig.2 Convolutional operation

对j行k列神经元的输出[15]为

(1)

式中：x,y分别代表卷积核的宽度和高度；b代表共享偏向；wl,m代表共享权重；αj+l,k+m代表输入层的激活值；σ是激活函数，一般激活函数都是非线性函数。Sigmoid 是常用的非线性的激活函数，其数学表达式为

(2)

Sigmoid函数和Relu函数如图3所示。

图3 Sigmoid函数和Relu函数Fig.3 Sigmoid function and Relu function

图3中，Sigmoid函数能够把输入的连续实值“压缩”到0和1之间。特别地，如果是非常大的负数，那么输出就是0；如果是非常大的正数，那么输出就是1。Sigmoid函数有一个非常致命的缺点，即当输入非常大或者非常小时，这些神经元的梯度接近于0，导致网络很难学习下去。为了避免这种趋势，本文采用Relu函数，其数学表达式为

f(x)=max(0,x)。

(3)

从图3中可以看到：当输入较大时，Relu函数的梯度是恒定的；当输入小于0时，Relu函数的值为0，对负输入有抑制作用。Relu函数具有更好的稀疏性，能有效解决Sigmoid函数梯度消失的问题。

1.2 下采样层

在通过卷积获得了特征图之后，下一步希望利用这些特征去做回归。CNN的下采样是一个进一步缩小矩阵的维数、同时不破坏数据内在联系的过程。

本文采用的最大下采样(Max Pooling)是指选取图像区域的最大值作为该区域池化后的值，如图4所示。

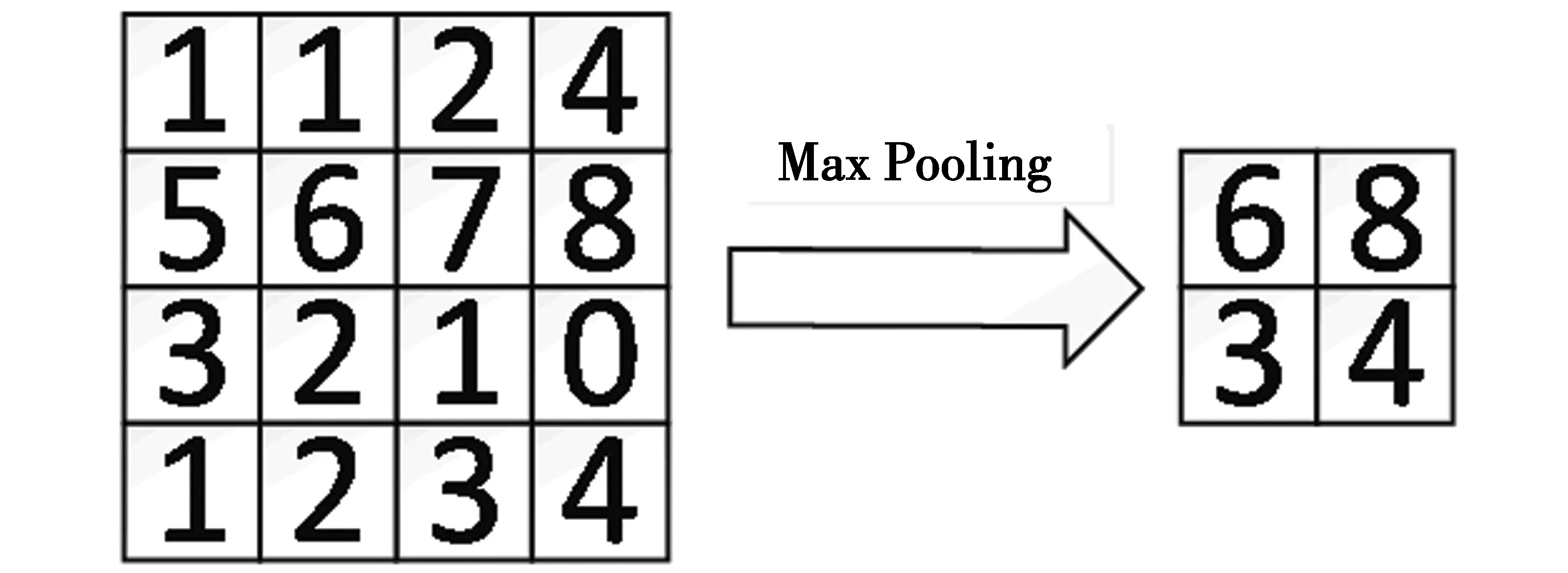
图4 Max Pooling操作Fig.4 Max Pooling

最大下采样能够减少特征提取时因卷积层参数误差造成的估计均值偏移，能更多地保留图像的纹理特征。数字图像中每个领域的4个像素取最大值变为1个像素[16]，具体表示为

(4)

式中：Ai,j表示下采样前的像素值；bi,j表示下采样后的像素值。

1.3 输出层

输出层由4个神经元组成，每个神经元分别代表目标漫反射系数(gDiffuse)、目标镜面反射系数(gSpecular)、地面漫反射系数(bDiffuse)、地面镜面反射系数(bSpecular)。将实际图像作为输入就可以得到4个仿真参数的估计值,以实现对仿真参数的预测,将得到的仿真参数输入电磁仿真软件可得到仿真图像。

2 实验结果分析

2.1 实验平台和数据集

本实验在Google开源深度学习框架tensorflow上进行，采用Windows7操作系统，Intel xeon e5 2683处理器，内存192 GB，GPU为Tesla K80的计算机，进行CNN训练。实验使用的训练样本是2700幅SAR图像和每幅图像对应的4个仿真参数，其中，2600幅图像进行训练，100幅图像进行测试。

2.2 多维回归的损失函数

目前线性回归模型的损失函数[17]为

(5)

(6)

图5为2种不同的损失函数的变化曲线，比较两条曲线可以看到损失函数都收敛，并且损失函数的值比较接近。

图5 2种损失函数的变化Fig.5 The change of two loss functions

为了观察训练时每一维仿真参数的变化，画出每一维的参数误差幅值，其中参数误差幅值为

(7)

图6所示为4个仿真参数的误差幅值变化。

图6 不同仿真参数误差幅值变化Fig.6 Variation of error amplitude of different simulation parameters

图6中:蓝色线代表式(5)的损失函数对应的每个参数的误差幅值变化;红色线代表式(6)的损失函数对应的每个参数的误差幅值变化。可以看出，随着训练轮数的增加，误差幅值变化越来越小，比较红蓝色曲线可以看到，使用式(6)的损失函数的误差幅值变化明显小于使用式(5)的误差幅值的变化。

2.3 测试结果与误差分析

图7所示为4个仿真参数的真实值与预测值的比较。图中，黑色曲线代表实际100个测试数据的真实值，红色曲线表示线性回归的预测值，蓝色曲线代表式(6)的损失函数的神经网络的预测值，青色的曲线代表式(5)的损失函数的神经网络的预测值。

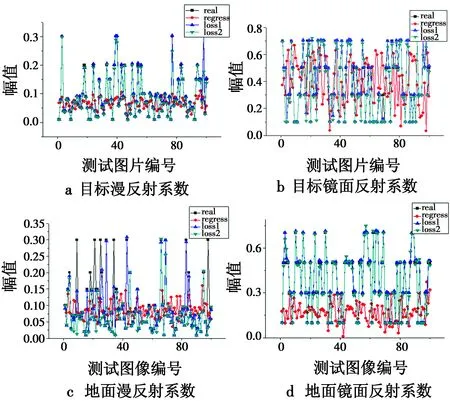
图7 预测值与真实值比较Fig.7 Comparison of predicted and real values

从图7可以看到，红色曲线与黑色曲线相差比较大，说明线性回归误差比较大，仿真参数与输入图像之间的关系难以用线性模型来表达。而蓝色曲线和青色曲线与黑色曲线的拟合度比较好，说明神经网络的预测方法明显好于线性回归的方法。从图中可以看到，对于目标漫反射系数、目标镜面反射系数和地面镜面反射系数，蓝色曲线和青色曲线对真实值的预测比较相似，但是对于地面漫反射系数，蓝色曲线的拟合度明显好于青色曲线，说明式(6)的损失函数对每个仿真参数的预测都有很好的效果。对地面漫反射系数有些点的预测还是存在比较大的差异。造成这一现象的原因可能是由于训练数据集比较小，可以增大数据集；也有可能是训练集中的地面漫反射系数的数值分布比较集中，可以在取数据集时尽量使仿真参数的值服从正态分布。通过对比曲线的拟合程度可以证明模型具有比较好的预测效果。

2.4 仿真图像和真实图像比较

图8所示为3组真实图像和仿真图像的对比，上面3张是真实图像，下面3张是其对应的仿真参数图像。

图8 真实图像与仿真图像对比

由图8可以看出，仿真图像和真实图像具有非常高的相似度，证明了仿真参数回归方法的正确性。

3 结束语

本文设计了一种11层的CNN用于SAR图像电磁仿真参数的回归，将仿真得到的2700幅图像和其对应的仿真参数分为训练集和测试集，其中，2600幅图像用来训练，100幅图像用来测试。对于这种多元多维的回归方法，提出了一种新的损失函数来进行训练，该损失函数对于每一个维度上的数据都有很好的预测效果。最终使用训练出来的神经网络得到最佳仿真参数，利用最佳仿真参数进行电磁仿真得到仿真图像，并且和真实图像进行对比，仿真图像和真实图像具有非常高的相似度，证明了仿真方法的有效性。