移动机器人速度跟踪视觉伺服控制

刘江涛，陈奕梅

(天津工业大学 电气工程与自动化学院，天津 300387)

0 引 言

视觉传感器相较于其它传感器视觉传感器可以获得更为丰富的环境信息，随着图像处理与计算机视觉技术的发展，视觉传感器越来越多的被应用到机器人运动控制领域，从而进一步加强了机器人的灵活性并扩展了机器人的工作空间[1-5]。文献[6]对视觉伺服系统的最新研究成果进行了详细的介绍，其中对于移动机器人上搭载单目摄像机的视觉伺服控制系统的研究，主要集中在提高视觉系统对图像噪声、特征误差匹配等因素的鲁棒性和对移动机器人运动控制的实时性、灵活性的进一步改善。文献[7]中提出了一种基于单应性矩阵的切换控制算法，实现了移动机器人的视觉伺服镇定。Mezouar等提出基于图像的轮式移动机器人视觉路径控制方案，视觉伺服方面采用基于几何约束的信息反馈：对极几何或三焦张量[7]。

本文采用的2DTT即二维三焦点张量，2DTT视觉信息采集系统与单应矩阵相比能够充分利用二维图像中的信息，从而获得机器人在视觉场景中的估计值与真实值之间的固定比例关系，进而可以得到机器人在运动中的唯一的相对位姿关系。文献[9]在采用2DTT估计机器人实时位姿的基础上采用了一种反馈线性化控制器以实现机器人的位置镇定，但对于2DTT中的未知深度问题并未实现自适应控制。

文献[10]中采用单应矩阵实现了移动机器人的自适应伺服镇定，本文在文献自适应伺服镇定的基础上采用了2DTT来进行视觉信息的采集。文献[11]提出了通过滑模算法使移动机器人的速度趋于期望值而实现轨迹跟踪。考虑到在机器人视觉伺服控制的过程中存在由于期望速度与机器人实际运动速度差值过大，引起的抖动问题，本文采用将自适应控制镇定器得到的运动路径作为虚拟轨迹，采用滑模速度跟踪控制来使机器人的实际运动速度趋于期望速度，来解决机器人镇定过程中的抖动问题。

1 视觉场景描述

1.1 视觉场景中机器人的坐标系关系

图1中给出了机器人视觉伺服过程中的坐标关系描述，如图Di，Dr，De分别表示机器人的初始位姿，当前位姿，期望位姿坐标(本文中将摄像机坐标系与机器人做重合处理)。坐标De中ze坐标轴为机器人前进方向，xe坐标轴为机器人轮轴方向，ye轴垂直地面向下(对Di，Dr坐标系的描述同上)。β为zi轴与ze轴的夹角，φ为zr轴与ze轴夹角。Pi为特征点中的第i个点。(注：本文中的坐标定义符合右手定则，β，φ取逆时针方向为正)

根据上述场景描述下可以得出从De到Dr的旋转矩阵为Rre与平移向量tre，从De到Di的旋转矩阵为Rie与平移向量tie

(1)

(2)

其中，sφ、cφ分别为sinφ、cosφ的简写，sβ、cβ分别为sinβ、cosβ的简写。

以De为参考坐标系得出De,Dr,Di对应的摄像机矩阵分别为Qe,Qr,Qi[8]

(3)

1.2 视觉系统测取的信息分析

对于特征点Pi在坐标系De,Dr,Di中的真实位置坐标为分别为Pei,Pri,Pii，特征点Pi在坐标系De,Dr,Di中摄像机采集到的图像上的坐标为分别为pei,pri,pii。

由摄像机的成像原理可以得到，在同一参考坐标系下，特征点的真实坐标Pi与摄像机采集到的图像坐标pi有如下关系

(4)

其中，K为摄像机的内参数矩阵，zi为特征点在参考坐标系下前向轴的真实坐标。

则可以得到Pi在参考坐标系下的归一化坐标

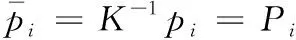
(5)

1.3 机器人的运动学模型

本文镇定控制采用机器人极坐标运动学模型

(6)

如图1所示，式(6)中的运动模型是以De为参考坐标系建立的，用(zer,xer)表示机器人在De下的相对当前位置，θ表示从机器人当前位置到期望位置的向量与ze轴正方向的夹角。α为从机器人当前位置到期望位置的向量与zr轴正方向的夹角，e为从机器人当前位置到期望位置的向量的模。

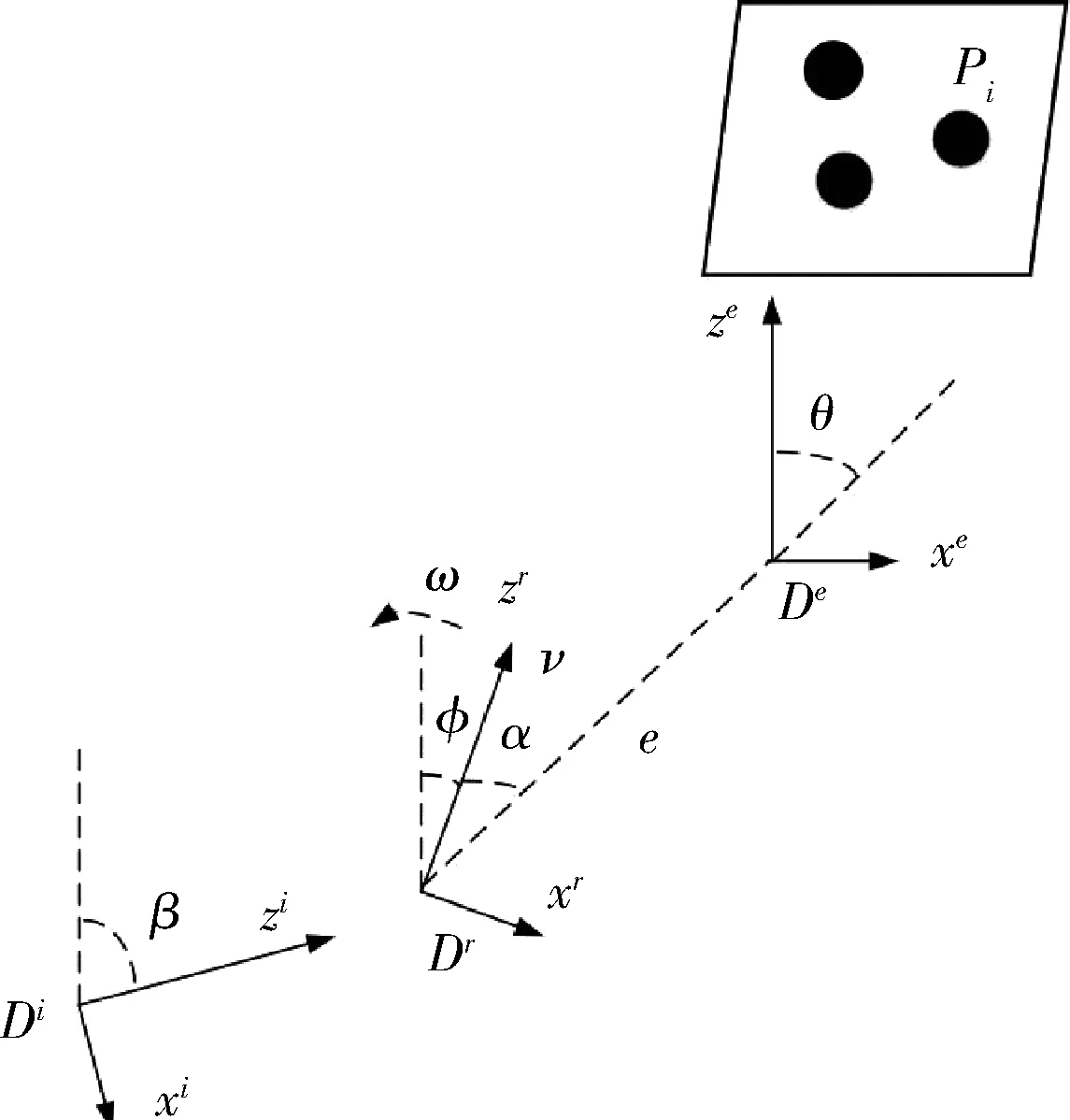
图1 机器人视觉伺服过程中的坐标关系

2 采用2DTT估计机器人位姿

2.1 三角点张量矩阵的推导

三角点张量的矩阵为H={T1,T2,T3}，其中

(7)

H与摄像机矩阵(3)的关系如下[8]

Tj=qij(qr4)T-qi4(qrj)T

(8)

其中，取j=1,2,3,qij,qrj分别表示Qi,Qr的第j列，qi4,qr4分别Qi,Qr表示的第4列，整理可得出

(9)

式(9)中给出了本文相关的两个运算变量的整理结果，具体的整理结果可以参见文献[12]。

2.2 估计机器人的位姿信息

H与Pi在De,Dr,Di下对应的归一化图像坐标有如相关系[12]

(10)

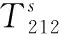
(11)

采用De与Di之间的实际距离L对H进行归一化有

(12)

(13)

其中，因为估计的位姿信息与实际的位姿信息仅相差一个比例因子，所估计的角度值与实际值相等。

3 自适应控制器

3.1 估计位姿的运动学误差模型分析

由式(6)、式(13)得出

(14)

根据式(6)、式(13)可以得出在视觉估计的机器人在极坐标下的开环运动学误差模型为

(15)

当es，α，θ趋于0时机器人可以从当前位置到达期望位置，所以本文采用自适应控制器控制式(15)中的误差量趋于零。

3.2 控制器设计

设计自适应控制器为

(16)

由于视觉估计的位置信息与实际的位置之间相差一个未知量k∈R+，所以需要针对这个未知量设计一个更新律

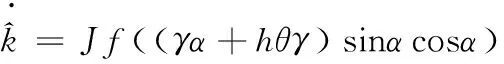
(17)

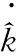
(18)

(19)

控制器稳定性验证取Lyapunov函数如下

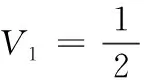
(20)

对V1求导并将式(16)代入得

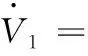
(21)

其中

(22)

由式(17)和式(19)可以得出

(23)

由式(18)中限制条件可得

F•≤0

(24)

4 动力学滑模控制器设计

以De为参考坐标系，如图1所示移动机器人运动学模型为

(25)

非完整约束条件为

(26)

移动机器人动力学模型为

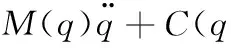
(27)

将式(25)求导代入式(27)得

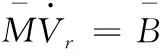
(28)

其中，τ=[τrτl]T，τr,τl分别为右轮和左轮的输出力矩

(29)

m为机器人质量，r为驱动轮半径轮，驱动轮轴为2L，I为转动惯量。

取τ1=(τr+τl)/r，τ1=L(τr+τl)/r则可以写为

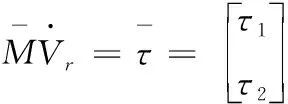
(30)

将自适应控制器的输出速度信号作为期望速度Ve=[vω]T，则对于实际速度Vr速度误差σ，选择如下滑膜面实现滑膜控制

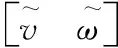
(31)

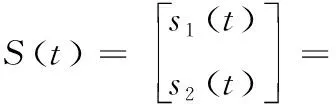
(32)

其中，η=[ηd1ηd2]T为滑模积分常数且η∈R+。

对式(32)求导并将式(30)、式(31)代入得

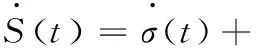
(33)

(34)

切换控制器τsw

(35)

其中，ζ1，ζ2>0。

则动力学控制器为

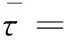
(36)

控制器稳定性验证取Lyapunov函数如下

(37)

对求导得

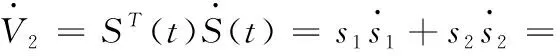
(38)

5 实验分析与验证

机器人参数m=33 kg,2L=0.5 m,d=0.4 m,2r=0.19 m。其中，m为机器人质量，2L为机器人直径，d为机器人两轮轴间距，2r为驱动轮的直径。

实验中参数设置如下机器人的初始位姿为(-1.05 m,-1.18 m,-0.49 rad),机器人的期望位姿为(0 m,0 m,0 rad),自适应控制器参数为λ=0.1,l=0.23,H=051,J=0.12,kmin=1.56。

图2～图5均为采用滑模速度控制后的实验曲线图，图2为运动轨迹图。图3中为位姿误差收敛曲线，e1为距离误差，e2为机器人朝向角误差。图4为线速度变化曲线，(图4～图7中点划线为自适应控制器得出的期望速度，实线为通过采集机器人轮转速折算出的实际的运动速度),图5为角速度变化曲线，图6、图7给出了未采用滑模速度控制的线速度变化曲线和角速度变化曲线。

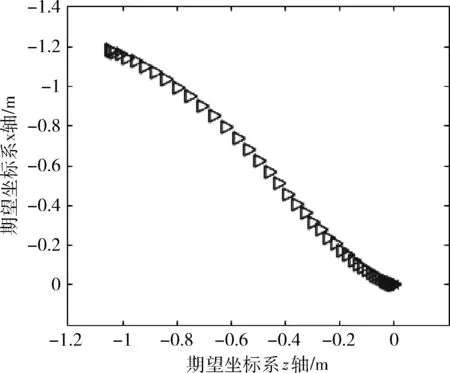
图2 机器人运动轨迹

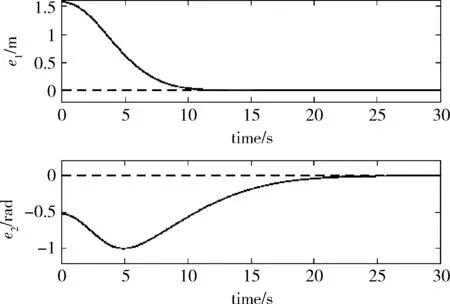
图3 位姿误差收敛曲线

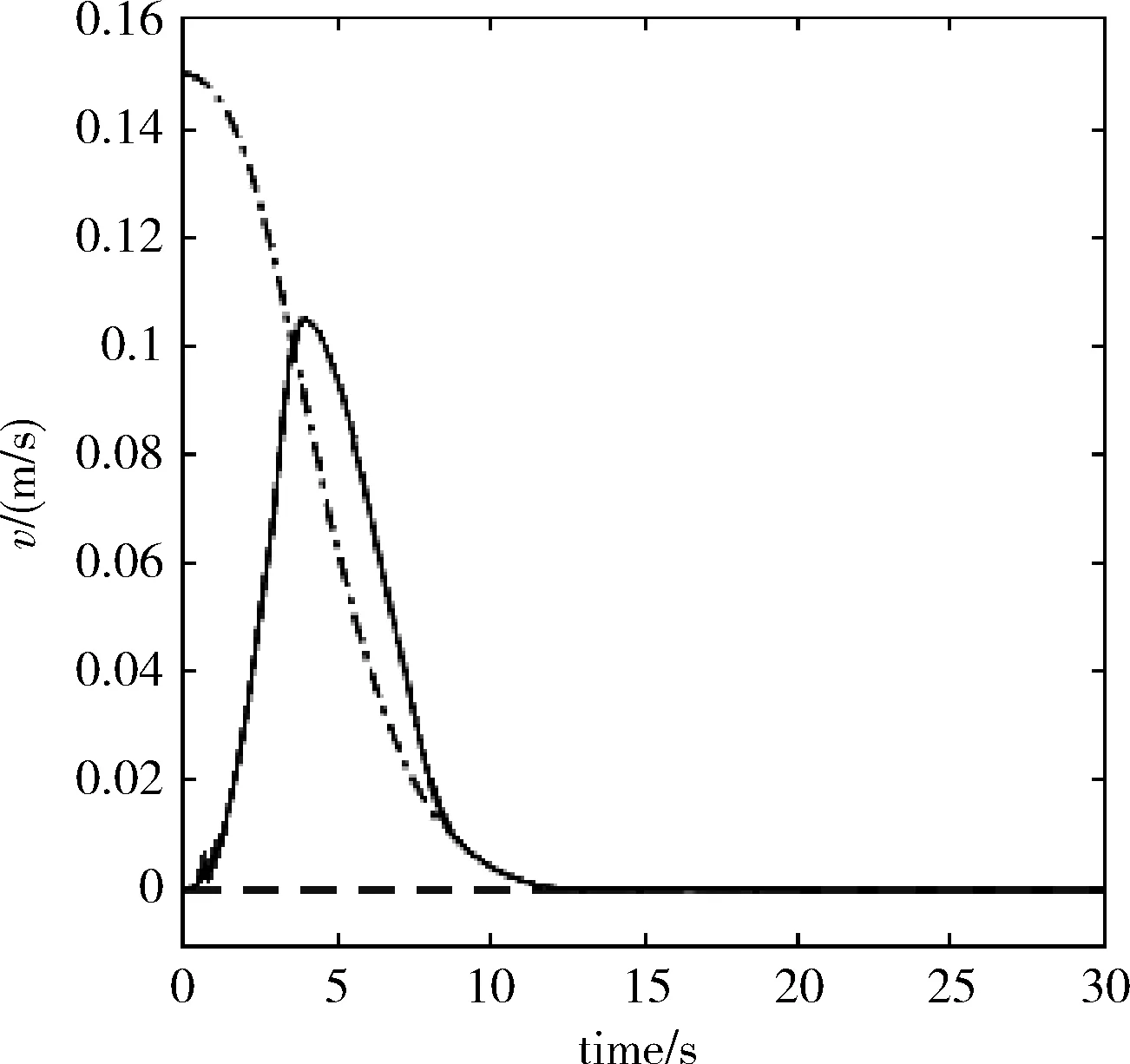
图4 线速度变化曲线

图5 角速度变化曲线

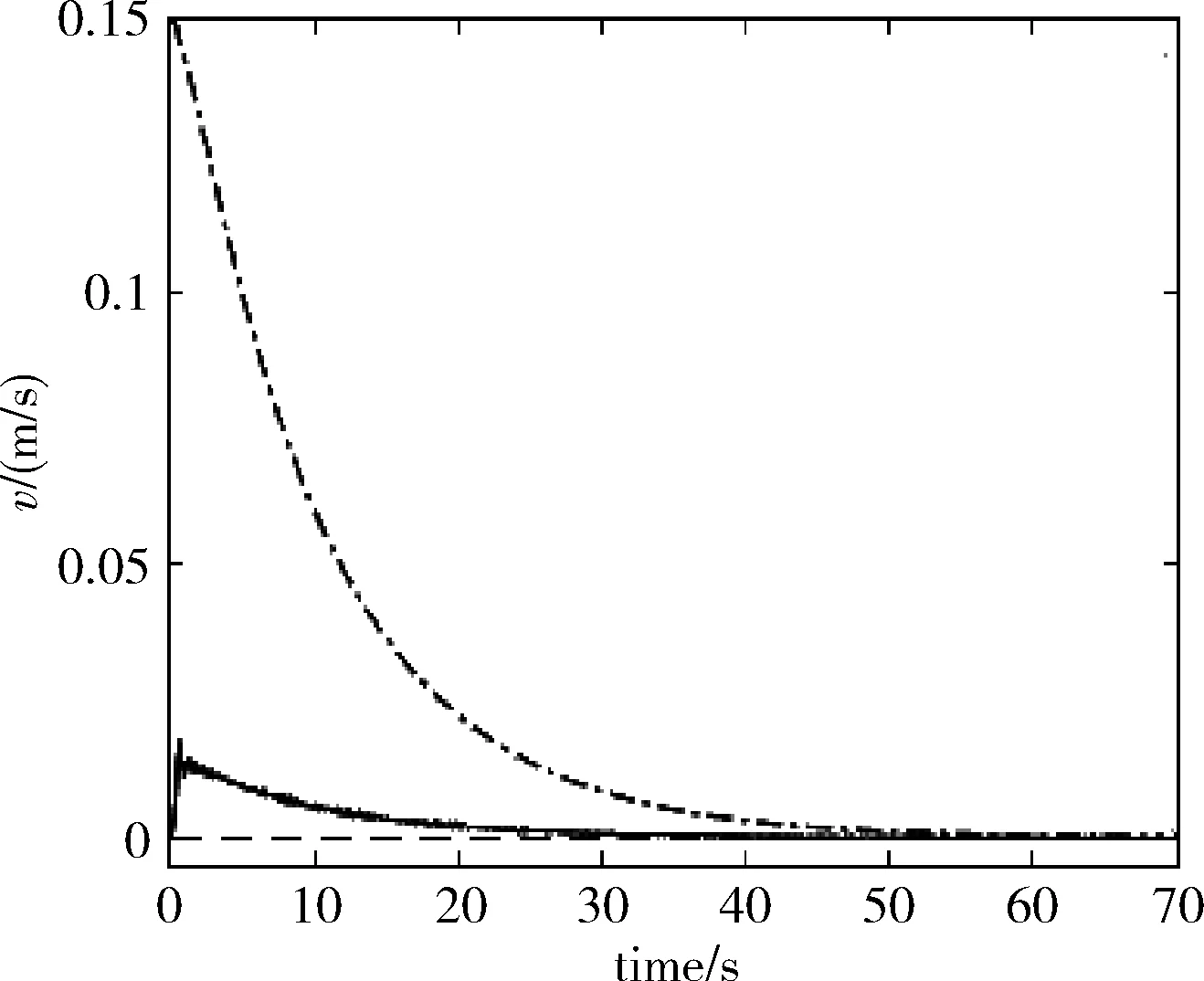
图6 未使用滑模控制线速度变化曲线

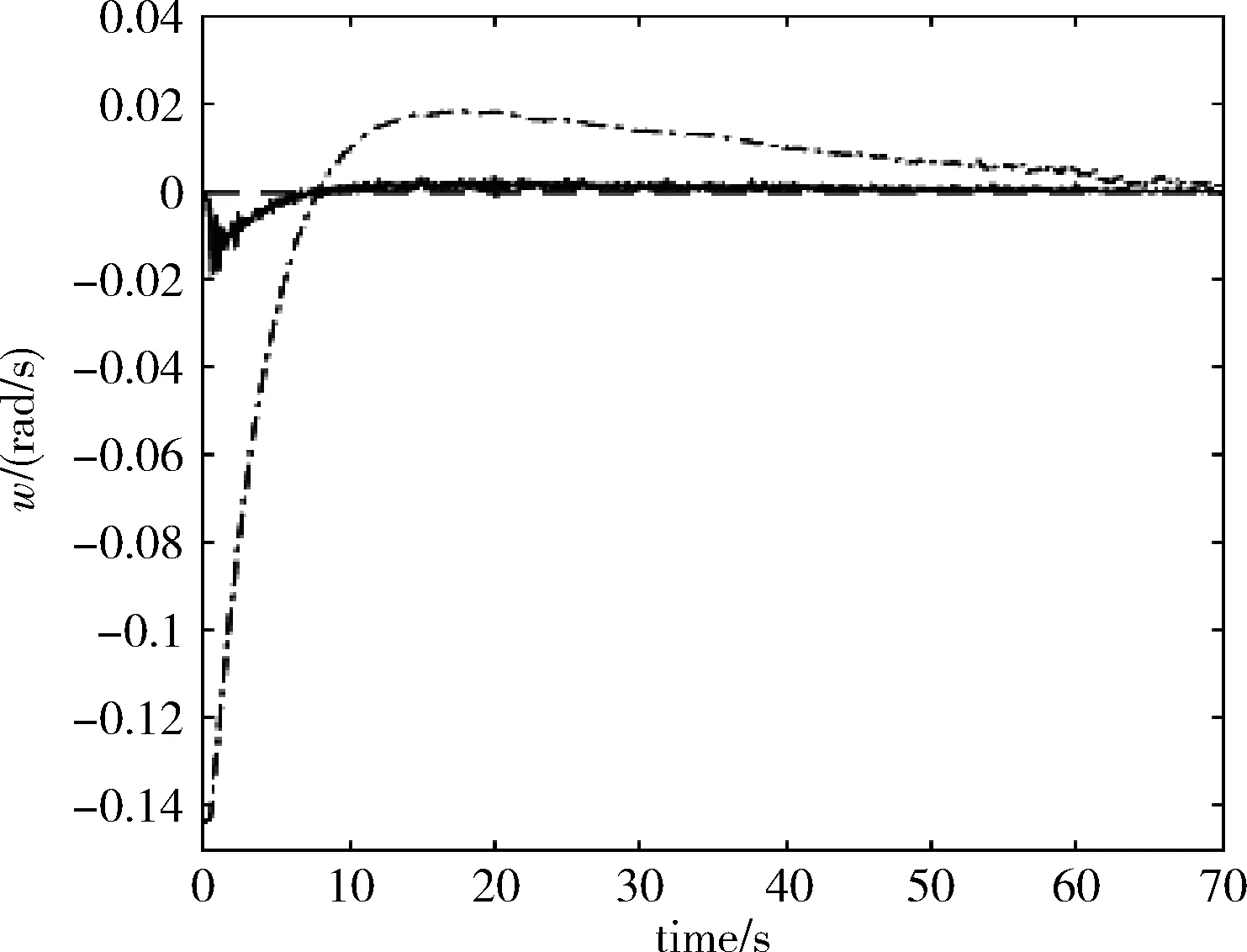
图7 未使用滑模控制角速度变化曲线

通过图2～图5的收敛曲线可以看出本文提出的伺服系统具有良好的稳定性与收敛性能。2DTT可以充分利用二维图像中的信息，所以可以更为准确得到机器人在移动中的相对位置信息并且不受机器人运动状态的干扰，但是由于数据处理量较大，在控制机器人运动过程中存在是性较差的问题。由图6～图7的速度曲线可以看到在未使用滑模控制进行速度跟踪时，由于2DTT的实时性较差，实际的速度曲线与期望速度曲线存在较大的差值且存在一定的抖动。为了改善这一问题，在图4～图5的速度曲线中采用了滑模控制进行速度跟踪控，可以看出实际的速度曲线与期望的速度曲线间的差值明显减小且逐渐趋于一致，速度曲线的抖动问题也得到明显改善。由于实际速度趋于期望速度的过程变快也使机器人的运动速度在一定程度上得到提高，控制机器人到达期望位置的时间缩短，控制效率得到改善。

图8给出了和图2同次实验中特征点在图像平面上的运动轨迹，其中三角与星形分别为机器人在期望位姿处与初始位姿处对应的图像特征点。图9给出了自适应比例因子k的变化曲线。

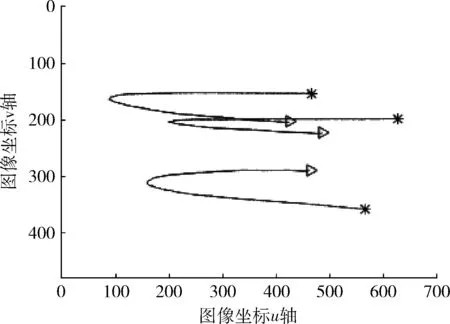
图8 特征点在图像平面上的运动轨迹

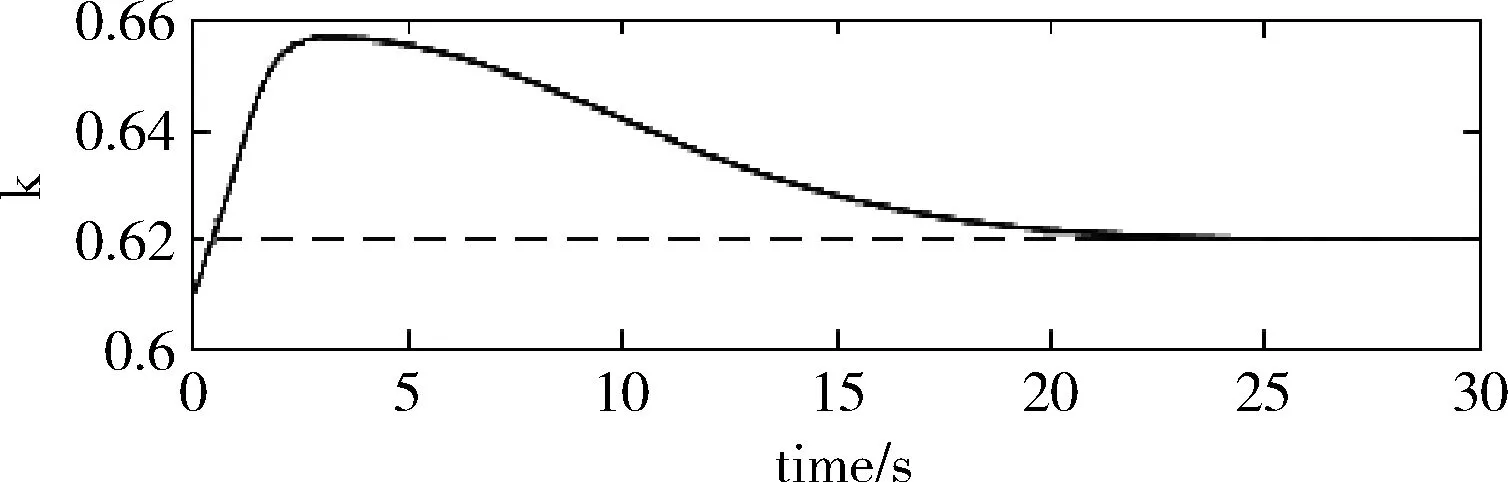
图9 自适应比例因子k

6 结束语

本文首先介绍了2DTT视觉信息估计方法，并在文献[10]中视觉伺服控制的基础上，采用比文献中具有更强视觉鲁棒性的2DTT来对机器人的实时位置进行估计。增强了视觉伺服系统的鲁棒性。并通过设计滑膜速度跟踪器，使机器人的实际运动速度趋于自适应控制器得出的期望速度，解决机器人在运动中存在的速度变化时的抖动问题，由于趋于期望速度使机器人的实际运动速度加快，可以加快机器人向期望位姿的收敛。通过实验分析验证了本文提出视觉自适应系统的鲁棒性和稳定性，以及滑膜速度跟踪的可行性与有效性。