基于近邻传播聚类与曲线拟合的断层识别

叶 涛，陈 雷

(1.青海民族大学 计算机学院，青海 西宁 810007；2.中国科学院地质与地球物理研究所 中国科学院油气资源研究重点实验室，北京 100029)

0 引 言

断层识别是地震解释中的重要环节，对油气资源勘探具有重要意义。为克服人工识别方法较为费时的不足，自动识别断层的方法获得了广泛的研究。

相干体算法[1](可分为三代：C1～C3)是最早出现的断层自动识别方法。它基于地震道之间的相关性对断层进行识别，但由于相关窗口的影响，所得断层的均值效应较为明显。Wang等通过Hough变换对相干体中直线的检测对断层进行了识别[2-4]，不足是对同时存在的多个断层的识别能力较差。Wang等先将实数地震道转换为复数形式，再基于复数形式的地震道利用相关方法识别断层[5]，不足是耗时较高，且有较多的层位信息残留。Di等[6]通过对地震层位在三维空间中的弯曲属性(方向和大小等)对小断层进行了识别，不足是计算复杂度较高。Yan等基于蚁群算法对断层进行了识别[7,8]。这种方法可将微小的断层识别出来，但所得断层结果的可信度不高。

断层识别方法中，人工方法最准确。故，最好的断层识别方法是用智能算法模仿人工方法的流程。模仿人工方法时层位不连续点的确定比较容易，基于层位不连续点的断层的生成是智能算法模仿人工方法成败的关键。

近邻传播聚类[9-11]是一种聚类算法，它可在未知聚类数目的情况下根据样本间的相似性对待聚类样本聚类。基于此方法，本文提出了一种基于近邻传播聚类与曲线拟合的断层识别方法。先采用连通区域标注方法确定层位不连续点，然后用近邻传播聚类算法对不连续点聚类，最后，用曲线拟合方法对每类不连续点进行拟合，模仿人工实现了对断层的识别。

1 近邻传播聚类算法

近邻传播聚类算法将所有数据点作为潜在的聚类中心，通过消息传递机制迭代地对数据点进行聚类并对聚类中心进行更新，直到聚类中心和对各数据点的聚类不在变化为止。

1.1 相似度与参考度初始化

相似度和参考度是近邻传播聚类算法中两个重要的输入参数，它们在一定程度上决定了最终的聚类结果，其初始化方法具体如下。

1.1.1 相似度矩阵的初始化

相似度矩阵中的元素表示相应样本点之间的相似性大小，这种相似性一般用欧式距离的负值来表示。比如，待聚类样本集Ω中的m和n两个样本点间的相似性的计算如式(1)所示

(1)

这样，两点距离越远，相似性越小，属于同一类的可能性越小；反之，属于同一类的可能性越大。

1.1.2 参考度的初始化

参考度决定了数据点可否作为聚类中心，对最终所得的聚类数目有重要影响。例如，当对图1(a)中所示的数据进行近邻传播聚类时(用欧式距离定义相似性)，最终所得聚类数目随参考度的变化曲线如图1(b)所示。

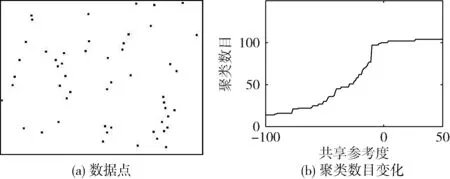
图1 参考度与聚类数目之间的关系

1.2 聚 类

采用近邻传播聚类算法对数据点进行聚类时，初始化好相似度和参考度之后，数据点和聚类中心之间传递吸引度和归属度消息，以此对吸引度、归属度和聚类中心进行不断的迭代更新，同时对数据点聚类，直至结果稳定。吸引度和归属度的传递方式如图2所示。

图2 吸引度和归属度传递

其中，r(i,k)为k点对i点的吸引度，反映了点k作为点i的聚类中心的合适程度，k′为竞争的候选聚类中心。a(i,k)为i点对k点的归属度，表示点i选择点k为聚类中心的合适程度，r(i′,k)表示其它点i′对点k作为聚类中心的支持程度。

迭代过程中，归属度、吸引度和自归属度的更新规则分别如式(2)～式(4)所示

s(i,k′)})+λ×r(t-1)(i,k)

(2)

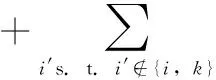
max0,r(t)(i′,k)}+λ×a(t-1)(i,k)

(3)

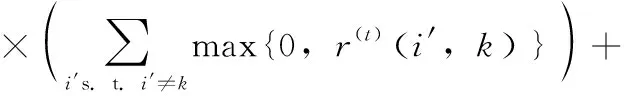
λ×a(t-1)(k,k)

(4)

其中，λ为阻尼系数，一般在0和1之间。

式(2)右端最大函数部分表示候选聚类中心k′比聚类中心k更好的证据。吸引度更新的意义是使所有聚类中心都参与竞争一个待聚类数据点的归属。

式(3)中，r(k,k)表示点k的自吸引度，r(k,k)为负值时表示点k不适合作为一个聚类中心。含最大函数的求和项表示候选聚类中心k从除i、k之外的点接收到的总的正吸引度。若某些点以点k作为聚类中心时的吸引度值为正，那么这些点以点k为聚类中心时的归属度值就会增大。这样，a(i,k)也表示了作为候选聚类中心的点k从所有数据点(除点i)接收的吸引度之和，体现了点k是否是一个好的聚类中心。

式(4)中，a(k,k)为自归属度，是点k作为一个聚类中心的证据总和。

每次迭代完成之后，近邻传播聚类算法对聚类中心进行更新并对数据点分类，规则如式(5)所示

(i,k) = argmax {a(i,k) +r(i,k)}

(5)

以式(5)所得结果(i,k)作为聚类依据时：如果i=k，则将点k作为新的聚类中心；否则，将点i归属到以点k为聚类中心的类别中去，实现对点i的聚类；直至聚类中心和每个点所归属的类别稳定，近邻传播聚类终止。

2 本文基于近邻传播聚类与曲线拟合的断层识别

本文所提断层识别方法的具体实现过程如图3所示。

图3 本文方法流程

其中，读入地震数据部分完成地震数据格式的转换，将地震数据转换成二值图像的工作在预处理部分完成，确定层位不连续点的确定工作在确定层位不连续点部分通过连通区域标注[12,13]方法来完成，对层位不连续点的聚类工作在近邻传播聚类部分完成，曲线拟合部分对每一类层位不连续点进行曲线拟合，获得断层，最后，将断层识别结果输出。

2.1 地震层位不连续点确定

2.1.1 地震层位提取

地震数据中正层位与负层位交替出现，若只保留地震剖面中的正层位部分，断层的数量、形状、位置等信息并不会受到影响，所以，本文只保留正层位(下文中的层位均指正层位)。地震层位的提取过程如下：

(1)将浮点型二维地震数据映射成二进值图像；

(2)对所得二值地震剖面图像进行形态学滤波；

(3)对滤波后的二值地震剖面进行连通区域标注，将地震层位作为连通区域提取出来。

2.1.2 地震剖面中层位不连续点的确定

地震剖面中层位不连续的地方即为断层，所以断层的位置可以通过层位不连续点来确定。本文将层位所对应连通区域的横向端点(包含左端点和右端点)作为层位不连续点，其确定方法如式(6)和式(7)所示

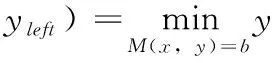
(6)

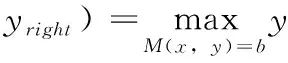
(7)

其中，xleft表示左端点的行坐标，yleft表示左端点的列坐标，xright表示右端点的行坐标，yright表示右端点的列坐标，x表示横向端点的行坐标，y表示横向端点的列坐标。M为标记矩阵，用于存储各个连通区域的标号。y为待优化的目标函数。M(x,y)=b为优化函数的约束条件，b为当前待确定横向端点的层位所对应的连通区域的标号。地震剖面图像中地震层位不连续点的确定方法如图4所示。

图4 确定地震层位不连续点原理

其中，H表示层位(与连通区域相对应)。L和R分别表示层位的左端点和右端点，即层位不连续点。

2.2 层位不连续点聚类

要正确地识别断层，需要对层位不连续点聚类以基于同类的层位不连续点来生成断层。本文采用近邻传播聚类算法，根据确定同一条断层的层位不连续点之间的相似性对其进行聚类，用同类层位不连续点确定一条断层。在聚类时，本文对相似度矩阵与参考度的初始化具体如下：

鉴于确定同一条断层的层位不连续点之间水平梯度差和欧氏距离均较小，本文用层位不连续点之间水平梯度差和欧氏距离加权和的负值来定义相似度矩阵，如式(8)所示

ω2*Gy(i)-Gyj}

(8)

其中，s为相似度矩阵，i和j分别表示不连续点中的第i和第j个点。xi表示第i个点的行坐标，xj表示第j个点的行坐标，yi和yj分别相应的列坐标。ω1表示相似性中欧式距离的权重，ω2表示水平梯度差的权重。Gy(i)表示第i个点的水平梯度，Gyj表示第j个点的水平梯度。由式(8)可知，两个层位不连续点之间相似性大小与欧式距离和水平梯度差均为反比关系。

在对参考度进行初始化时，本文用相似度矩阵各列的均值作为参考度的初始值，以使每一个层位不连续点都可以成为聚类中心。参考度的初始化方法具体如式(9)所示

(9)

其中，p为参考度向量，p(k)表示用于判断第k个数据点是否可以作为聚类中心的参考度，η为常数，一般取10左右，N为需要聚类的层位不连续点的个数，s表示相似度矩阵。近邻传播聚类过程中，以s(k,k)作为参考度，s(k,k)越大，第k个点越有可能成为聚类中心。

通过以上步骤就实现了地震剖面中层位不连续点的确定以及聚类，接下来就可以基于聚类后的不连续点进行断层的生成了。

2.3 断层最小二乘曲线拟合

采用近邻传播聚类算法对层位不连续点聚类之后，每一类层位不连续点可确定一条断层。本文提出了用最小二乘曲线拟合来确定断层的方法。

最小二乘曲线拟合是根据已知数据找出拟合多项式函数的系数，使得拟合出的函数值与原离散点的误差平方和最小。设N个点的x坐标(自变量)分别为x1,x2,…,xN，相应的坐标(函数值)分别为y1,y2,…,yN,k次拟合多项式函数为：p=a0+a1x+a2x+…+akxk，则拟合多项式函数值与误差平方和可以表示为

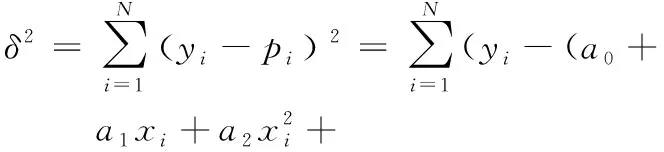
(10)

其中，pi为拟合多项式函数在第i个自变量xi处的函数值。最小二乘拟合的目标是找出最佳的一组系数a0,a1,…,ak，使误差平方和δ2最小，即通过下式找出p

(11)

将式(10)右边各项以依次对ai,i=1,2,…,k求偏导数并化简，可得

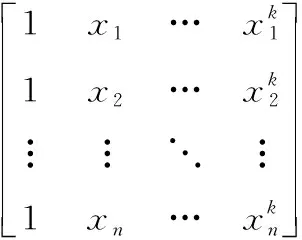
(12)

式(12)又可表示为

X×A=Y

(13)

由此可得

(14)

这样就得到了系数ai,i=1,2,…,k，也就得到了k次最佳拟合多项式函数的解析表达式，从而可以获得各个拟合多项式函数值pi,i=1,2,…,N。

对于同一类别中的层位不连续点，将每个点的行坐标作为自变量，列坐标作为函数值，利用最小二乘拟合即可得出与原有离散的层位不连续点误差平方和最小的连续曲线，即断层。

3 实验结果和分析

为验证所提基于近邻传播聚类与曲线拟合的断层识别方法的有效性，将其与人工断层识别方法、经典的C3方法和参考文献[7]中所提的方法在大小为220×290×100的实际地震数据上进行了仿真实验对比。计算机配置：系统：windows7，内存大小：4 G；实验工具：Matlab2015a。

各方法在某实际地震剖面上所得的断层识别结果的对比如图5中所示。

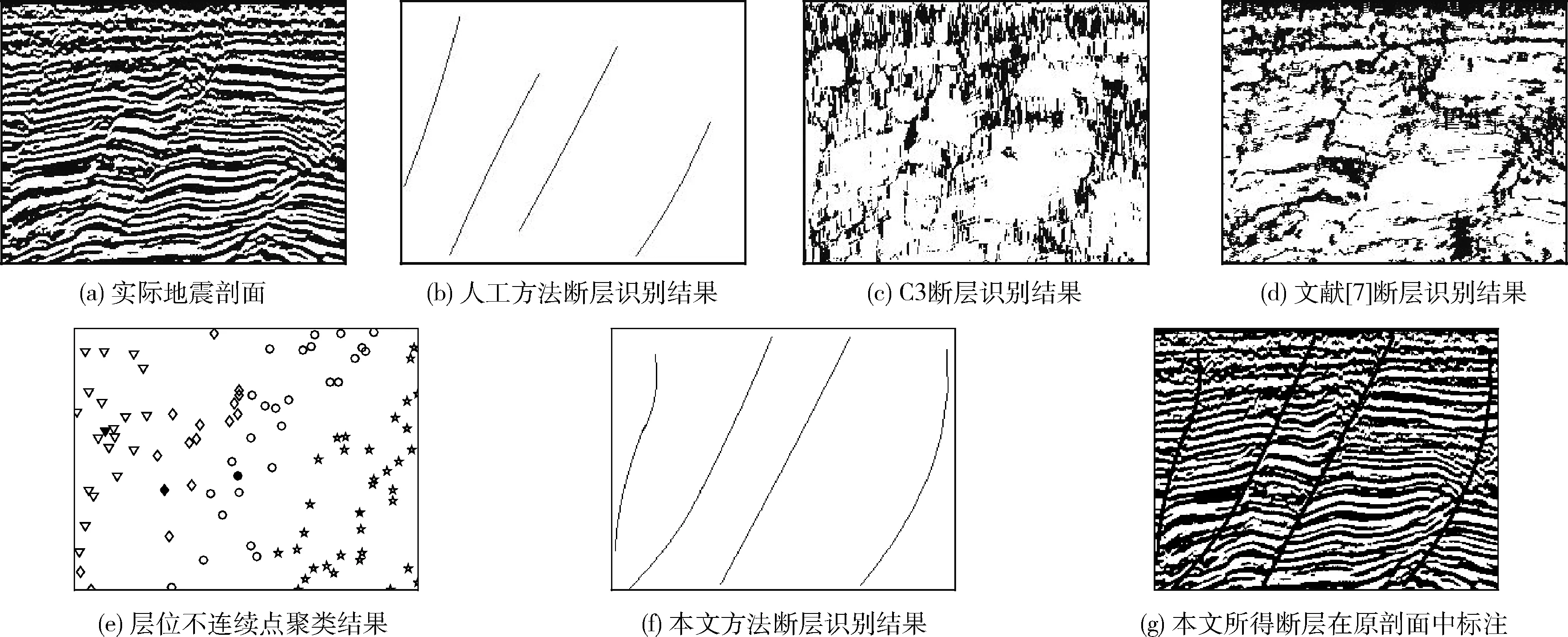
图5 本文方法与其它方法识别所得断层结果对比

由图5可知，人工方法识别所得的断层最准确，约与实际情况一致；由于均值效应的存在，C3方法所得的断层较为模糊，仅可以看出断层的大体形状和位置；文献[7]提出的基于方向复值相关属性的方法，在准确度方面比C3方法都有了提高，断层位置更加清晰，但有较多的层位信息残留下来；本文所提基于近邻传播聚类与曲线拟合的断层识别方法所得断层的准确度优于C3方法及文献[7]中所提的方法，从本文所提断层识别方法的可行性得以验证。

为了从客观指标方面进一步验证本文方法相对于其它方法的优越性，本文以采用人工方法识别出的断层为基准对各方法进行了客观指标对比，这些客观指标包括峰值信噪比(即：PSNR)、时间消耗和正确率，实验中采用了100幅地震剖面。对比结果如图6～图8所示。表1是各种方法的平均客观指标对比。

由图6所示的不同方法所得识别结果的信噪比对比可知：文献[7]中所提方法所得结果的信噪比最低，原因断层结果中有较多的层位信息残留；C3方法所得结果的信噪比也较低，与文献[7]中方法相近，原因是相关性计算所带来的均值效应。

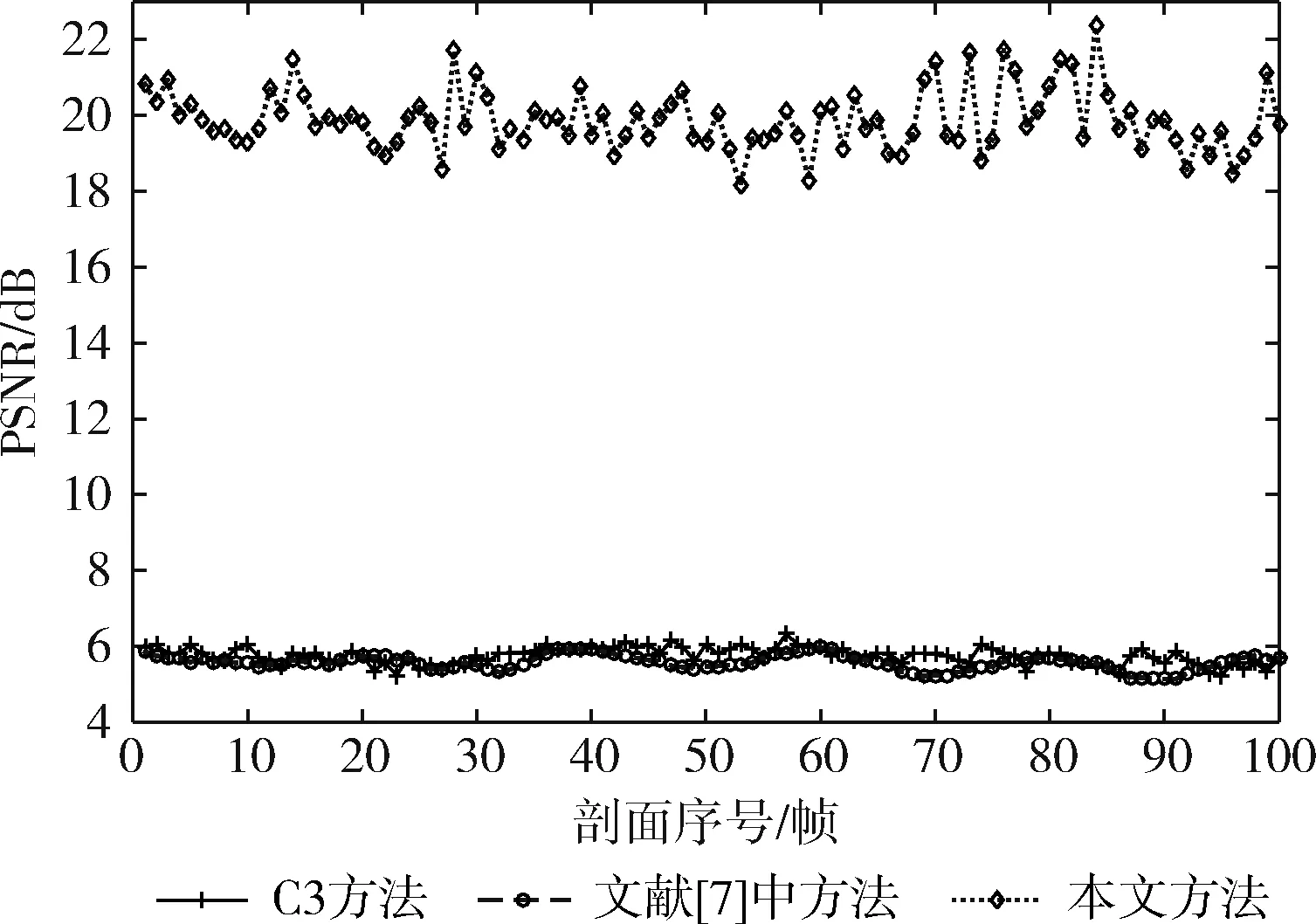
图6 各方法所得识别结果的峰值信噪比对比

图7中所示是采用不同方法对实验中的100帧地震剖面数据进行断层识别时的时间消耗对比；由图7中所示的时间消耗曲线可知：C3方法时间消耗最多，这是因为地震剖面中每一个地震样点都需要计算其所在地震道与立体窗口内其它各地震道之间的相关系数，计算量较大；文献[7]中方法时间消耗相对于C3有所降低，但依然较大，原因是它虽然没有像C3那样计算立体窗口内各个地震道与目标样点所在地震道之间的相关系数，但仍然计算了立体窗口内与水平方向成0°、45°、90°以及135°4个方向上各个复值地震道与目标样点所在复值地震道之间的相关系数；人工方法的时间消耗变化较大，这与人的主观性有关；本文方法的时间消耗最小，原因是本文方法去除了较为耗时的求相关计算，时间消耗主要是对少数的层位不连续点进行聚类和拟合。这就从时间消耗方面验证了本文所提方法的实时性。

图7 各方法时间消耗对比

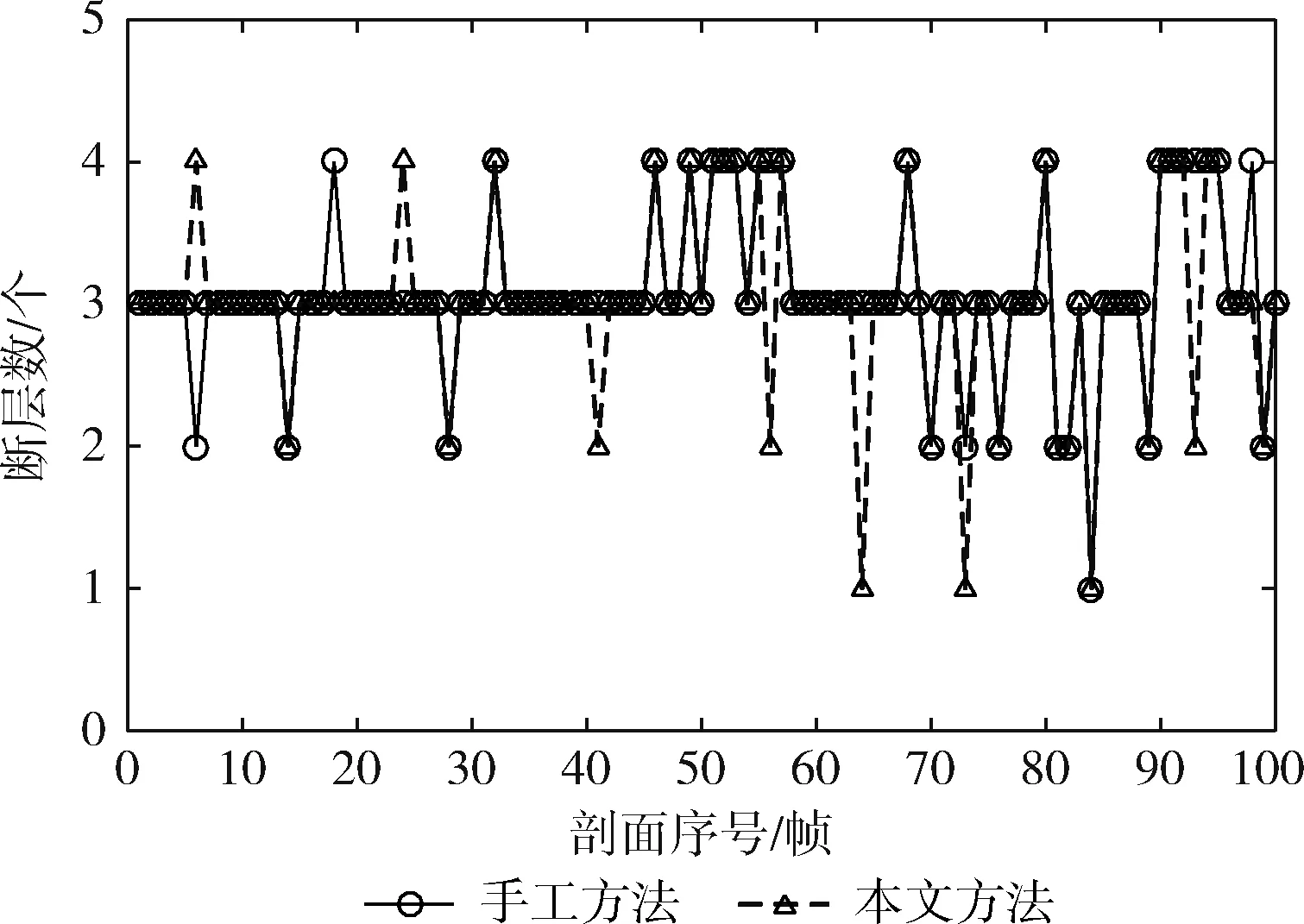
图8 本文方法与人工方法识别所得的断层数量比较

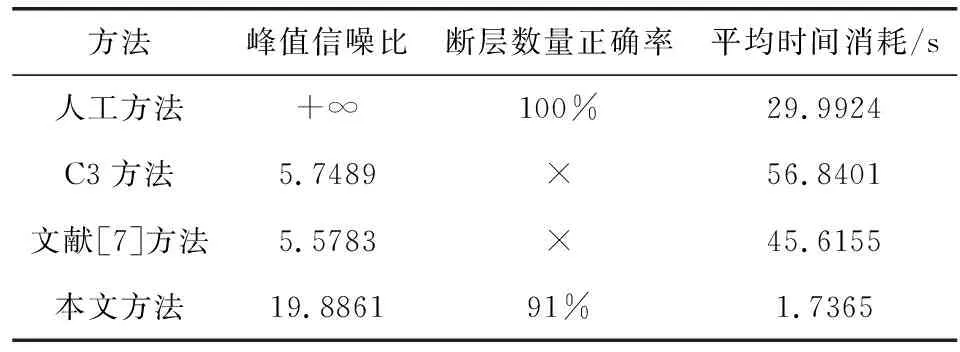
方法峰值信噪比断层数量正确率平均时间消耗/s人工方法+∞100%29.9924C3方法5.7489×56.8401文献[7]方法5.5783×45.6155本文方法19.886191%1.7365

图8中所示是本文方法与手工方法在每帧剖面上所得的断层数对比。可知，本文基于近邻传播聚类与曲线拟合的方法从每帧地震剖面中识别出的断层数与人工方法识别所得的数目基本吻合，从而验证了其识别正确率。

表1是采用不同方法所得断层结果的平均客观指标对比。因为PSNR和识别正确率都是以人工方法所得断层识别结果作为标准的，所以人工方法所得断层结果的平均PSNR为正无穷大，平均识别正确率为100%；因为C3方法、文献[7]方法不能提供量化的断层识别结果，所以在表1中用“×”表示它们的平均正确率。表1中各客观指标的对比进一步验证了本文所提方法的有效性和先进性。

4 结束语

针对现有断层识别方法所存在的准确性差、时间消耗大的问题，基于近邻传播聚类和曲线拟合，本文提出了一种新断层识别方法。文中先是介绍和分析了传统断层识别方法的优缺点；接着给出了本文所提方法的原理及实现步骤；最后，将本文方法与现在常用的人工方法以及基于方向复值相关属性的方法在实际地震数据上进行了实验对比，在所得断层识别结果的客观指标等方面验证了本文所提方法的可行性及实时性。如何定义相似度矩阵和设置参考度的初始值以使近邻传播聚类算法最终所得的聚类数量与人工方法所得出的断层条数更加一致，是本文进一步研究的工作。