基于最优运动矢量预测过程的改进与优化
蔡 宜,周金治+
(1.西南科技大学 信息工程学院,四川 绵阳 621010; 2.西南科技大学 特殊环境机器人技术四川省重点实验室,四川 绵阳 621010)
0 引 言
运动估计(motion estimation,ME)过程占据了视频压缩编码总体时间的70%(单帧参考)~90%(5帧参考)[1,2],其中庞大的运算量使得在实时视频编码过程中效果不佳,如果能减少ME的运算量将会显著提高整体编码效率。为解决上述问题,UmhexagonS算法[3]被H.264/AVC纳入采用,相比以往算法,UmhexagonS算法在保证良好率失真的情况下节省了90%的运算量,但代价是需消耗相对较长的运动估计时间。文献[4]给出了一种基于方向的UmhexagonS算法,通过方向划分来确定搜索区域,缩减运动矢量搜索时间。文献[5]中提出了一种交叉十字划分,把搜索区域划分为4个小区域,然而该方法设置的预测精度过低,仍存在搜索冗余,这里标记为问题1。文献[6,7]中改进算法在剧烈运动情景中均节省了23.8%左右的运动估计时间,而在微运动情景中仅仅节省了7.4%左右,表明该算法在微运动情景下适应能力较差,这里标记为问题2。文献[8,9]均提到了动矢量具有中心偏置分布特性,然而后者在3×3区域改进算法中忽略了对中心点搜索,但中心点为最优运动矢量点的概率高达45.49%,这里标记为问题3。
本文将在UmhexagonS算法以及相关文献的基础上,从以上3点进行优化和改进。
1 UmhexagonS算法原理
UmhexagonS算法是一种混合运动矢量搜索算法,分为粗略搜索、细致搜索和精细搜索3个流程。算法基本流程如下:①联合使用多种预测模型确定起始搜索点;②进行非对称大十字搜索;③进行5×5矩形搜索;④进行扩展大六边形搜索,在此环节中,需由里到外进行4轮扩展搜索;⑤进行小六边形循环搜索,直到当前最优匹配点为搜索模板中心为止;⑥进行小钻石搜索,直到当前最优匹配点为搜索模板中心为止,此时算法结束。搜索模型如图1所示。
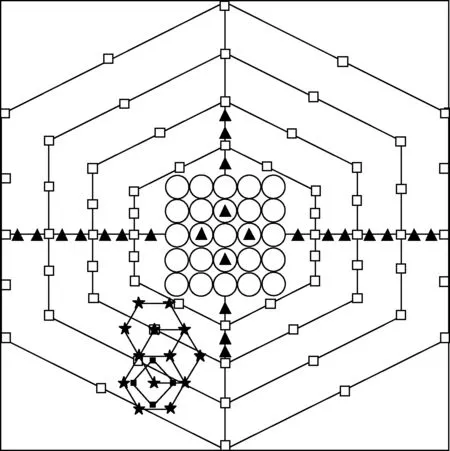
图1 UmhexagonS算法搜索模型
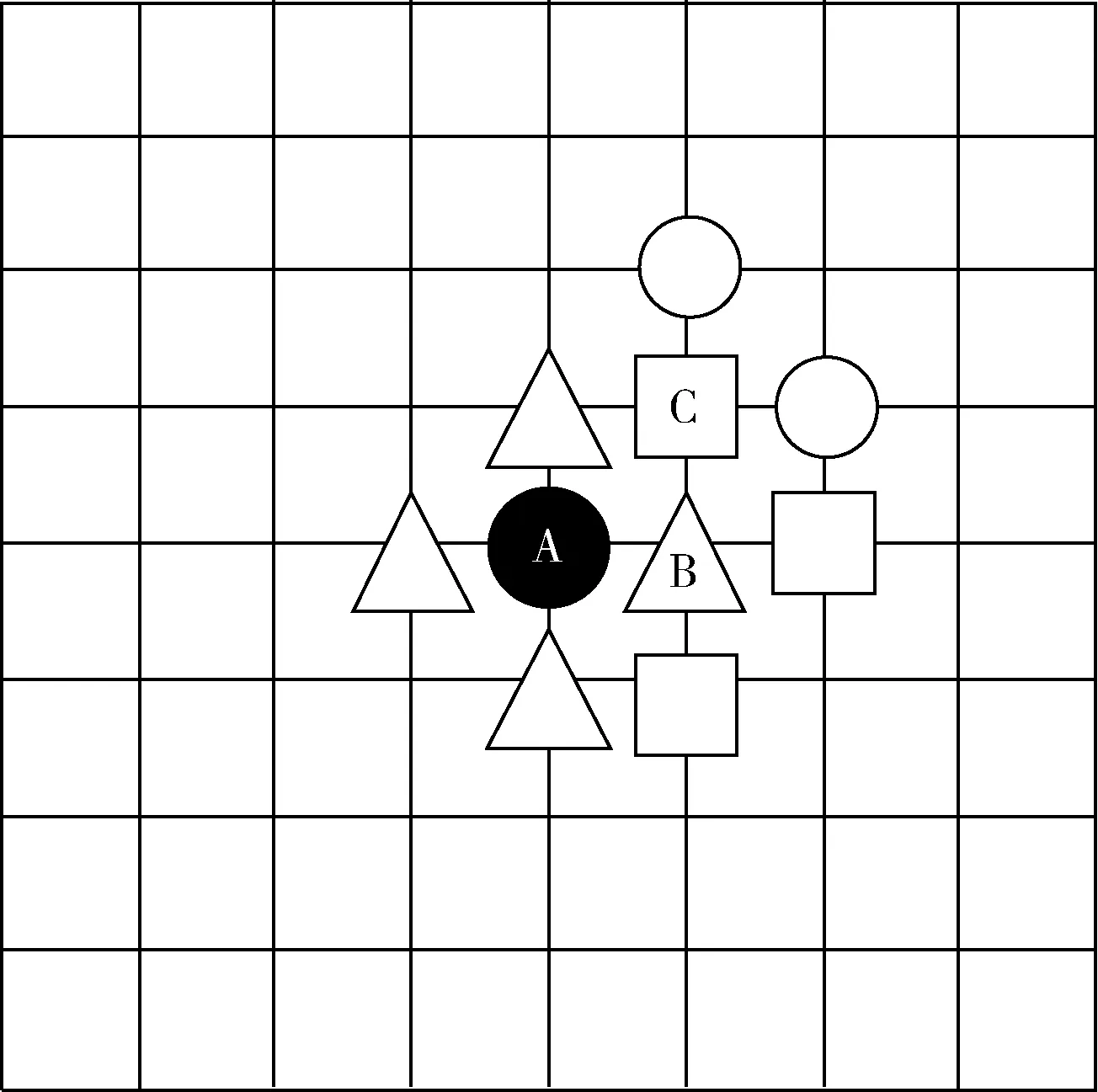
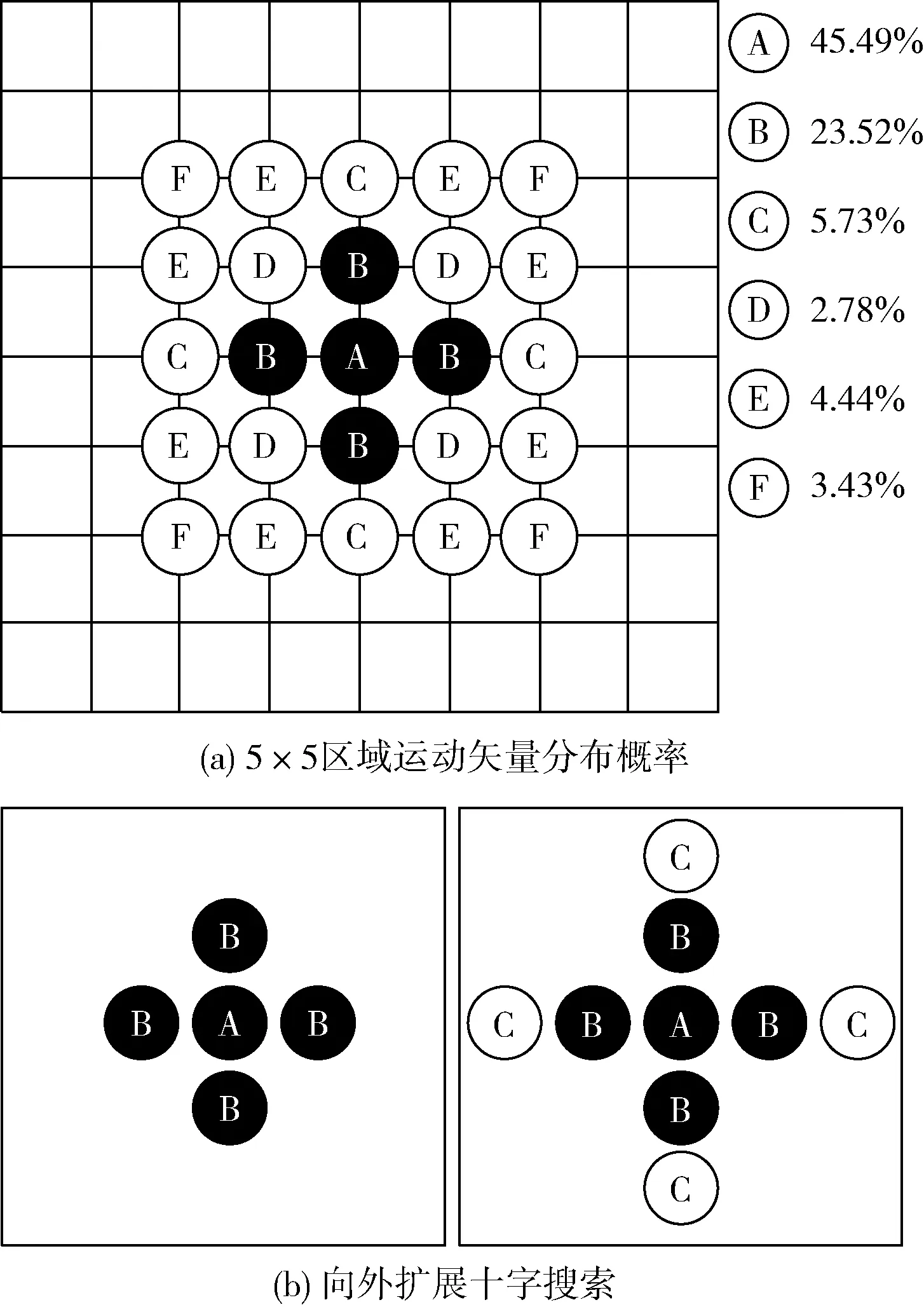
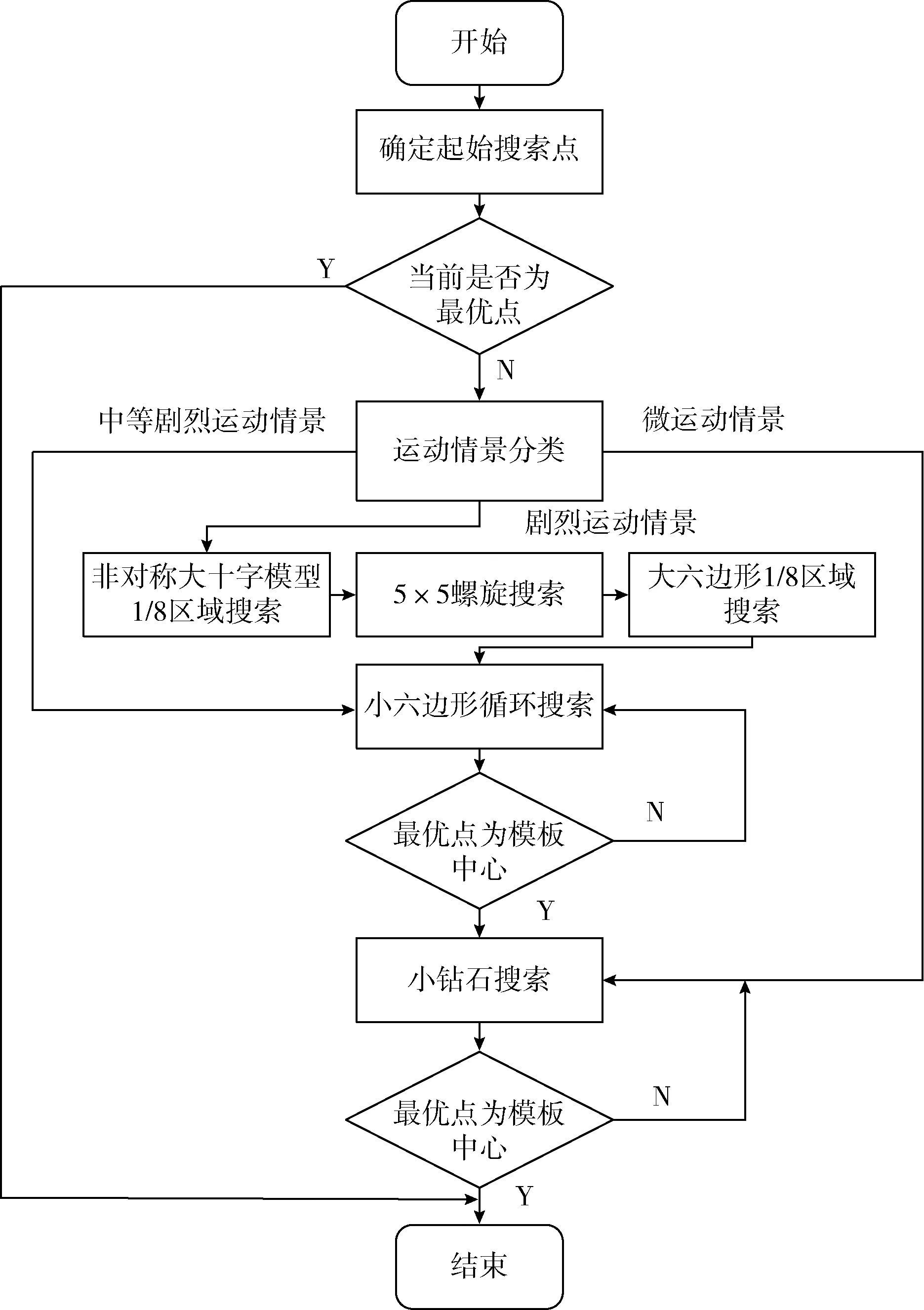
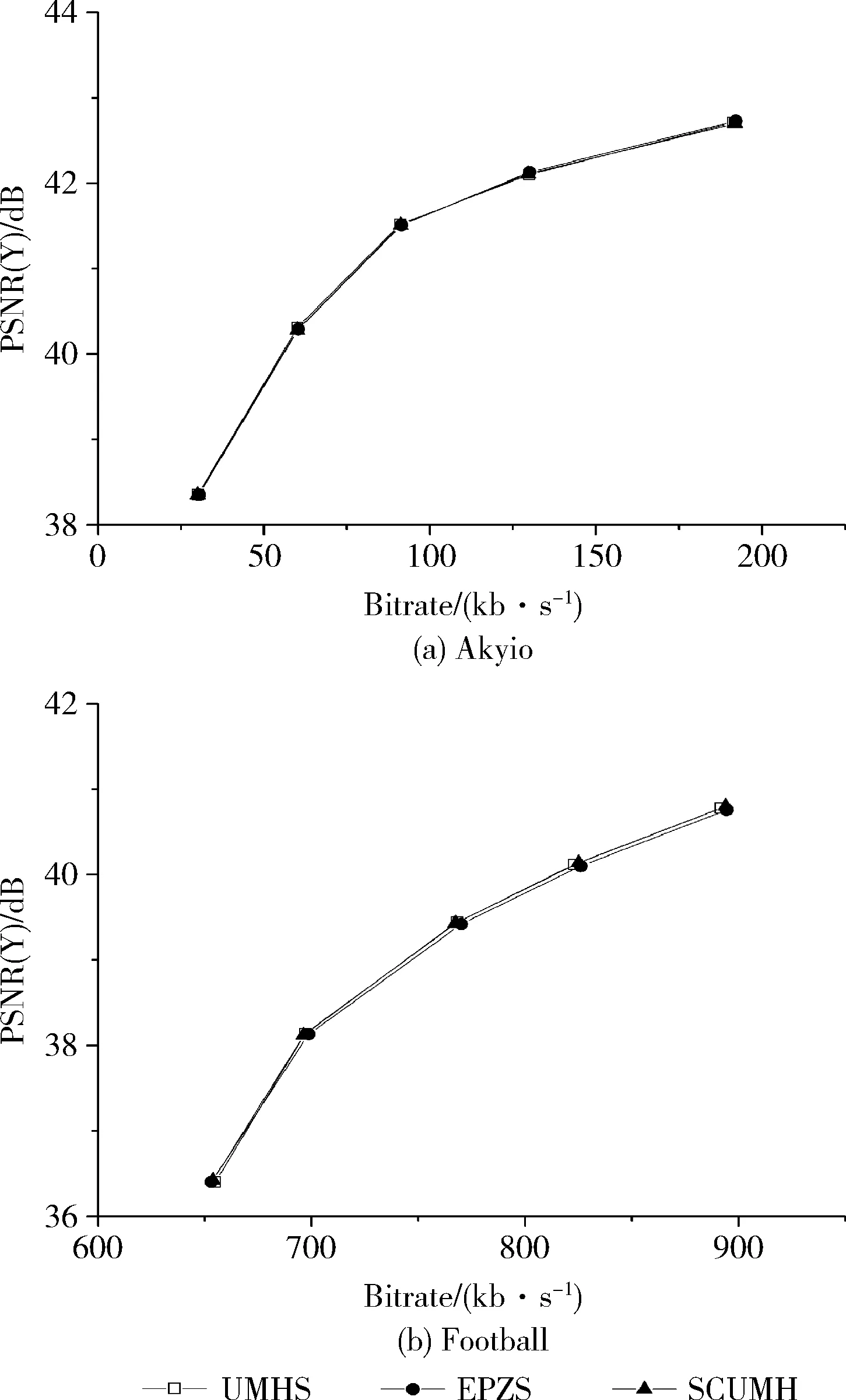
上述每步中均是以前一步得到的最优点为中心展开搜索;在步骤②~步骤③中均引入了判断阈值来提前终止搜索策略。对当前模板的最佳运动匹配矢量进行率失真代价计算,然后与预设阈值T进行比较。当SAD>T2时,继续执行下一步搜索;当T1 J(MV,λMOTION)=SAD(s,c(MV))+λMOTION× (1) 式中:SAD(sum of absoulute different)的计算公式如下 (2) 式中:s表示当前帧中[x,y]的像素值;MVx和MVy分别代表预测运动矢量的横向分量和纵向分量;λMOTION为拉格朗日常数;R(MV-PMV)代表了运动矢量差分编码可能损耗的比特数。由于当前运动矢量与预测运动矢量具有较强的相关性,所以SAD部分的预测特性完全可以反映整个匹配函数的预测特性,即J(MV,λMOTION)可以等效于SAD。 UmhexagonS算法利用起始点搜索预测和提前终止预测等策略使得MET(motion estimation time)得到缩减,并且保证率失真基本不变。然而,MET的缩减是以较高的计算复杂度为前提。若取默认的16×16搜索范围,那么在最坏情况下要搜索多达272个点,且对每个点进行匹配误差计算,这里的计算量是非常庞大的。 针对问题1,研究表明当前块的运动矢量和参考帧中预测运动矢量具有高度的相关性,因此可以通过两者对最优预测矢量的落入范围进行预测。假设预测精度满足规定的条件,那么最佳预测矢量必然是落入该范围的,此时只用搜索该区域。 (3) (4) 图2 前后参考帧预测矢量 根据θ即可确定搜索范围:①当θ∈[0,45°)或θ∈[-45°,0°)时,对应搜索区域1或8;②当θ∈[45°,90°)或θ∈[-90°,-45°)时,对应搜索区域2或7;③当θ∈[90°,135°)或θ∈[-135°,-90°)时,对应搜索区域3或6;④当θ∈[135°,180°)或θ∈[-180°,-135°)时,对应搜索区域4或5,如图3所示。 图3 大范围模型区域划分 区域划分策略将大范围搜索模板细化为8个区域,θ的值会将定位到特定的搜索区域。相比较UmhexagonS算法,改进后算法的搜索面积缩小到1/8,相比较文献[5]的十字划分,改进后算法的搜索面积缩小到1/4。 UmhexagonS算法中引入的非对称大十字搜索和扩展大六边形搜索很大程度上优化了对剧烈运动情景的预测效果。然而在微运动情景下,最优点通常都积聚在搜索中心点附近,如果仍使用大范围搜索模型会存在搜索冗余,降低效率。 针对问题2,文献[10]提出了一种自适应的模型切换算法,作者给出了一个基于EDR(error descent rate)模型的内容分类器。然而作者仅仅选取了中心点附近的4个点进行采样,其采样范围容易陷入局部最优。 依据单峰值误差面假设,当前块率失真往往随着与全局最优点距离的缩小而单调递减[11]。通常全局最优点与其周围像素点的关系比远处像素点的关系要密切很多,越是靠近全局最优点,其率失真代价越小,越是远离全局最优点,其率失真代价越大。依据这一性质,我们可以重新设定搜索策略,当为微运动情景时,采用局部小范围模型搜索;当为剧烈运动情景时,采用大范围模型搜索。 图4给出了最优点距离搜索中心越来越远的4种情况,取坡度比值分别为 (5) 其中,L1最靠近搜索中心点,坡度比最大;L4最远离搜索中心点,坡度比最小。由此我们可以通过计算搜索中心点与邻近点的坡度来估计最优点与搜索中心的距离。当坡度比值越大,最优点距离搜索中心越近;当坡度比值越小,最优点距离搜索中心越远。 图4 全局最优点与中心点距离的率失真表现 经过起始点预测后得到的当前最优点是全局最优点的概率非常大,那么将以当前起始预测点为中心,对其周围相邻点进行率失真代价计算(步长为一个像素)。图5中,点A是经过起始点搜索后得到的,率失真代价为DA,若测得此时周围邻近点DB为最小,那么搜索中心点与最邻像素点率失真差值为|DB-DA|。由之前讨论出的结论可知,即当|DB-DA|越大时,最优点离搜索点中心越近;当|DB-DA|越小时,最优点离搜索点中心越远。这里利用EDR模型,通过三步迭代搜索进行运动情景分类,每次搜索步长均为一个像素 EDR=D最小邻点/D中心点 (6) 图5 搜索中心点与周围邻点 (1)以起始搜索点A为中心点对邻域搜索,若测得点B为最小邻点,此时EDR=DB/DA。当EDR≥1时,表明此时已经局部最小,直接终止搜索;当EDR (2)以点B为中心点,若测得点C为最小邻点,此时EDR=DC/DB。当EDR (3)以点C为中心点,重复以上操作,当T≤EDR<1时,当前为剧烈运动情景。这里的阈值T依据参考文献设置为0.9。 改进后的算法直接分类出3种不同强度的运动情景。当为剧烈运动,仍然从非对称大十字搜索模型开始依次搜索;当为中等剧烈运动情景,直接从小六边形开始搜索;当为微运动情景,直接从小钻石开始搜索。 通过对大量自然运动序列分析,现实世界中大多数图像序列的块运动场通常是平滑、缓慢的,主要以水平运动为主。 经实验验证,约有85.39%的运动矢量非均匀的分布在5×5区域内,而其中分布在3×3区域的概率高达71.79%。由此可知,运动矢量的中心偏置性同样体现在了5×5小范围模板中,即搜索模板中心的运动矢量分布密度远大于边缘区域。针对问题3,本文采取了由内向外扩展的搜索顺序,如图6(a)所示,在3×3区域中D点的概率低至2.78%;5×5边缘地区(D+E+F)分布概率低至10.6%,故均予以忽略。首先对中心3×3小十字形进行搜索,然后再向水平方向扩展进行5×5大十字搜索,如图6(b)所示。对比原算法,改进后的5×5模板只需搜索概率最大的9个点(占5×5全局的87.52%),相比之下减少了16个点;相比文献[9],本文算法在增加了搜索中心点的情况下仍比其少搜索5个点,且搜索区域的最优运动矢量分布概率比其高34.84%。 图6 5×5区域运动矢量分布概率 综上所述,本文改进后算法流程如下:①确定起始搜索点;②进行运动情景分类,若为微运动情景直接跳转到⑦开始执行,若为中等剧烈运动情景直接跳转到⑥开始执行,若为剧烈运动情景则进行下一步;③计算当前MVC、MVPRE,进行非对称大十字模型1/8区域搜索;④进行改进后5×5螺旋搜索;⑤计算当前MVC、MVPRE,进行大六边形1/8区域搜索;⑥以前一步获得的最优点为搜索中心进行小六边形循环搜索,直到当最优匹配点为搜索模板中心为止;⑦以前一步获得的最优点为搜索中心进行小钻石搜索,直到当最优匹配点为搜索模板中心为止,此时算法结束。算法流程如图7所示。 图7 改进后算法总体流程框架 将本文改进后算法在官方参考软件JM12.2模型中进行测试,测试PC配置为Pentium(R) Dual-Core CPU E6300@2.80 Hz,4 G内存,操作系统Windows 7。开发环境为Visual Studio 2015。encoder.cfg主要参数设置如下:编码帧数为100;帧率为30;QP=28;搜索范围为16;参考帧数为5,其余均为默认设置。 本文共选取了6种运动强度情景不同的YUV(4∶2∶0)测试序列,分辨率均为176×144。缓慢运动序列:akiyo_qcif,news_cif;中等剧烈运动序列:foreman_qcif,coastguard_qcif;剧烈运动序列:mobile_qcif,football_cif。在测试过程中,测试项PSNR/dB、BR/(kb/s)、ENT/s、MET/s分别代表:Y分量峰值信噪比、输出码率、编码时间、运动估计时间。在测试结果中,分别用△PSNR(Y)/dB、△Br/%、△MET/%来表征算法性能,计算公式为 ΔPSNR(Y)=PSNR(Y)mod-PSNR(Y)ref (7) (8) (9) 其中,下标mod代表本文改进后算法值,下标ref代表对比算法的值。 表1对6组测试序列分别进行4类算法测试,其中SCUMH代表本文改进后算法。通过分析Full search、UmhexagonS、EPZS这3种参考算法在编码时间和运动估计时间中的数据,发现在缓慢运动情景下Full search最耗时,EPZS次之,UmhexagonS耗时最少;随着运动情景剧烈程度的增加,EPZS算法的性能逐渐超越UmhexagonS算法。分析可知,UmhexagonS算法在剧烈运动情景下性能不及EPZS算法,但在微运动情景下性能强于EPZS算法。 依据表2,改进后算法在剧烈运动情景下MET平均减少了40.53%;在中等剧烈运动情景下平均减少了32.86%;在微运动情景下平均减少了27.05%。对比参考文献[7],改进算法在剧烈运动情景下,MET进一步缩减了19.27%;在中等剧烈运动情景下缩减了15.17%;在微运动情景下缩减了19.45%。由以上数据可知,改进后算法不仅能极大减少剧烈运动的估计时间,在微运动情景下减少的MET也相当可观。在剧烈运动情景下,针对问题1提出的区域划分策略,缩小搜索面积,节省了在剧烈运动情景下的搜索时间;在微运动情况下,针对问题2提出的提前情景分类策略,自适应地选择搜索模型,提高了微运动情景下的搜索效率。同时,5×5搜索模型也改进效果明显。 图8,图9分别表示了两组不同运动强度测试序列的性能,由图可知,改进后算法在微运动、剧烈运动情景下均缩减了一定比例的运动估计时间,且随着编码帧数的增加,缩减比例也增加;同时,改进算法在率失真方面与UmhexagonS、EPZS算法基本一致,说明本算法保持了与原算法同样的率失真性能。 图9 Akiyo与Football在3种算法上率失真对比 本文以UmhexagonS算法在预测最优运动矢量过程中仍存在较长运动估计时间的问题展开。通过对比现有算法,提出了一种包含运动情景提前分类、大范围模型区域划分、5×5搜索顺序改进的3种改进策略的SCUMH算法。实验结果表明,对比UmhexagonS算法,在保证PSNR与码率基本不变的前提下,SCUMH算法不仅在剧烈运动情景中缩减了大量的运动估计时间,且在微运动情景下缩减时间也相当可观,可适应各种复杂多变的运动情景。 另外,SCUMH算法仍存在需要完善的地方:①本文采取的时间域预测方式(前后参考帧预测)可改进为在空间域的预测,因为在运动矢量预测过程中后者更为精确;②EDR运动情景分类模型过于粗糙,无法准确表示出中心点与周围邻点的偏离程度。
R(MV-PMV)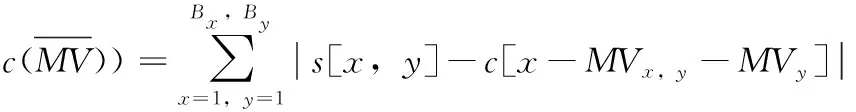
2 UmhexagonS算法改进
2.1 搜索区域改进

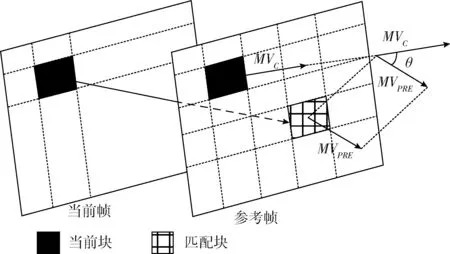

2.2 运动情景提前分类策略
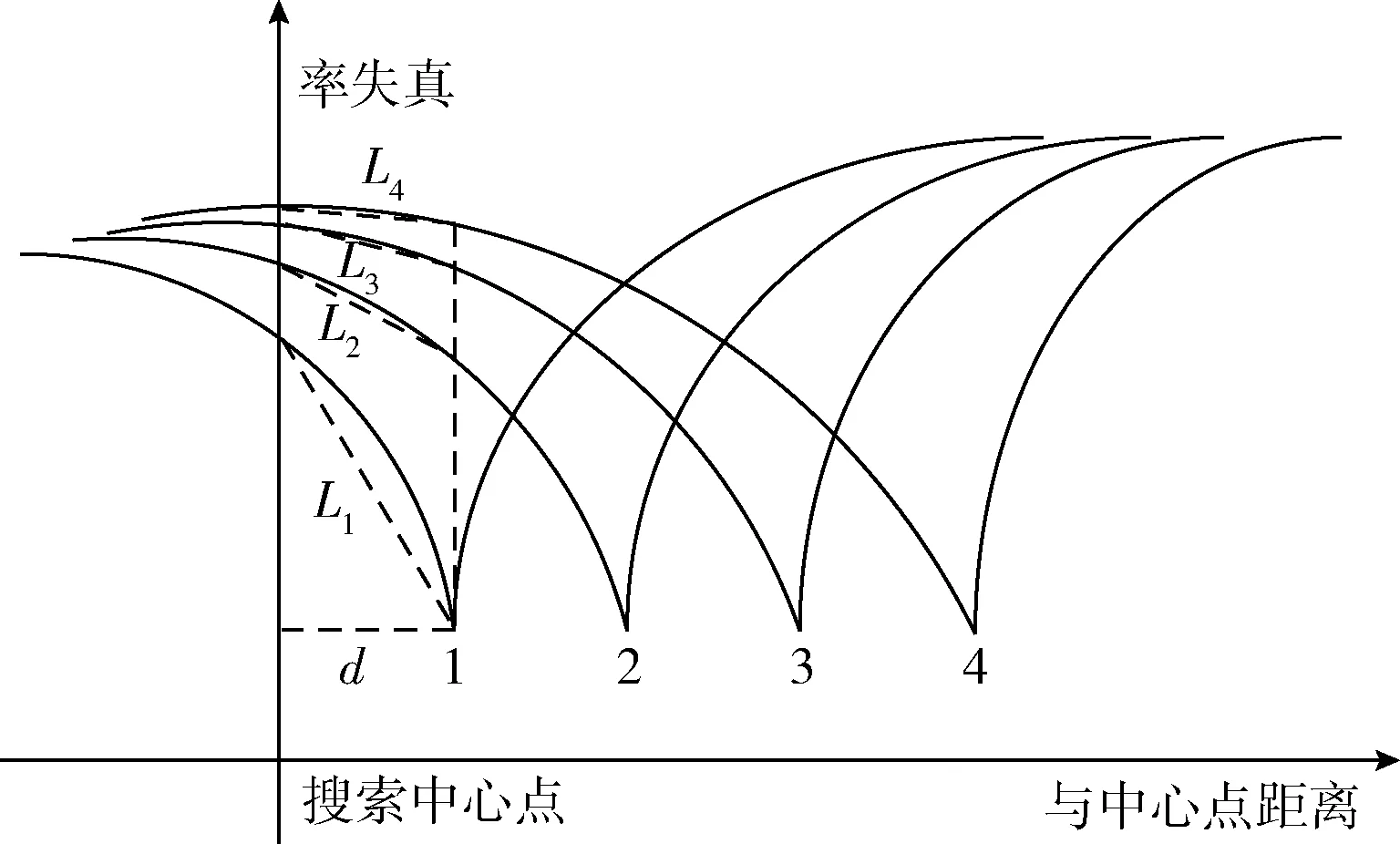
2.3 5×5螺旋搜索改进
2.4 改进算法总结
3 实验结果与分析
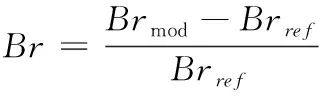

4 结束语

