中国股票市场的波动率聚集性研究——基于Markov机制转换Copu1a模型的实证分析

吴鑫育 ，李心丹，马超群

（1.南京大学 工程管理学院，南京 210093；2.安徽财经大学 金融学院，安徽 蚌埠 233030；3.湖南大学 工商管理学院，长沙 410082）

“波动率聚集”是指金融资产价格的变化往往大的波动后紧跟着大的波动（高波动率的聚集），小的波动后紧跟着小的波动（低波动率的聚集）。波动率聚集是金融资产收益率序列中的一个重要特征，它反映了波动率的正相关性（即后一期的波动率与前一期的波动率的相关性为正）。事实上，波动率的相关性是波动率建模和预测的前提和依据，而波动率是资产组合配置、风险管理及期权定价中的一个重要变量。因此，准确描述波动率动态特征，考察波动率的相关性结构（波动率线性、非线性相关性及高、低波动率的非对称相关性等），对波动率聚集性进行建模具有重要的意义，有助于加深对金融市场微观结构的了解，为投资者和风险管理者提供信息和决策参考。

传统上，学者们主要采用（G）ARCH模型和随机波动率（SV）模型来捕获波动率聚集性[1-3]。然而，这些模型并不能用于测度和解释波动率聚集性。近年来，学者们提出了新的模型对波动率聚集性进行了考察。文献[4-6]中提出基于Agent的模型来考察波动率聚集性；Jiang等[7]基于无标度网络模型对金融市场的聚集行为进行了考察；Tseng等[8]提出一个量化方法来测度波动率聚集性；Xue等[9]提出了一个离散时间多阶段的市场微观结构模型来考察波动率聚集性；Stádník[10]探讨了波动率聚集的金融学解释；Kumar[11]考察了波动率聚集对期权效用无差别定价的影响。

综上所述，已有研究主要考察的是正常市场条件下线性、对称的波动率聚集性，但对极端市场条件下的波动率聚集性及其可能存在的尾部非线性、非对称以及动态特征的考察还非常少见[12]，但是，文献[12]中没有考虑波动率聚集的动态性。鉴于此，本文采用Copula方法来捕获和测度中国股票市场的波动率聚集性。Copula方法是金融市场变量相关性结构研究中的一种重要方法，它能灵活且有效地捕获金融市场变量间复杂的相关性结构，如非线性相关性、极端市场条件下的尾部相关性、非对称相关性以及动态相关性等。此外，Copula允许对金融市场变量的边际分布与相关性结构分别进行建模，通过选择不同的边际分布和Copula来构造复杂的非正态联合分布，这使得建模的灵活性增加，有助于充分刻画金融市场变量（如波动率）的“偏斜”“尖峰厚尾”等非正态特征。因此，Copula在金融学文献中引起了众多学者的关注[13-14]。

传统静态Copula模型假定相关性参数是常数，不能捕获变量间的动态相关性结构。为了克服该问题，近年来，学者们提出了许多动态Copula模型，例如时变Copula模型[15-16]、半参数动态Copula模型[17]、随机Copula模型[18]以及Markov机制转换Copula模型[19-21]。Manner等[22]对这些动态时变Copula模型进行了综述，研究表明，Markov机制转换Copula模型相比其他动态Copula模型具有更为优越的数据拟合效果，且模型较为简单、易于实现。

鉴于Markov机制转换Copula模型在理论与实践中的优越性，以及为了弥补目前国内学者对中国股票市场的波动率聚集性研究的不足，本文通过考察极端市场条件下我国股票市场波动率的尾部相关性结构，选择合适的Copula函数，构建相应的Markov机制转换Copula模型，对中国股票市场的波动率聚集性进行研究，考察波动率聚集可能存在的尾部非对称、动态特征。

1 Markov机制转换Copu1a模型

1.1 模型构建

这部分构建Markov机制转换Copula模型来描述波动率聚集性（波动率期限结构）。令x t为股票收益率的波动率，波动率聚集性即由t和t-1时刻的连续波动率变量x t和x t-1的联合分布函数H（x t，x t-1）刻 画。根 据Sklar定 理，存 在 一 个CopulaC（·，·）：[0，1]2→[0，1]，使得

式中：u1=F（x t），u2=F（x t-1），分别为x t和x t-1的边际分布函数；θ为Copula的参数向量。可见，Copula是由均匀分布在区间[0，1]上的边际分布u1=F（x t）和u2=F（x t-1）构造的一个联合分布函数，它充分捕获了连续波动率变量x t与x t-1的相关性（波动率聚集性）。

基于Copula可以方便地测度两变量在极端市场情形下的尾部相关性，即两变量同时处于下（左）尾或上（右）尾的概率。连续波动率变量x t和x t-1的下尾和上尾相关系数分别为：

式中，λL，λU∈[0，1]。如果λL（λU）∈（0，1]，则x t和x t-1存在下（上）尾相关性；如果λL（λU）=0，则x t和x t-1不存在下（上）尾相关性。通过选择不同的Copula函数可以刻画不同的尾部相关性结构。实际中，常用的Copula函数及其各Copula函数的尾部相关性表达式如下所示：

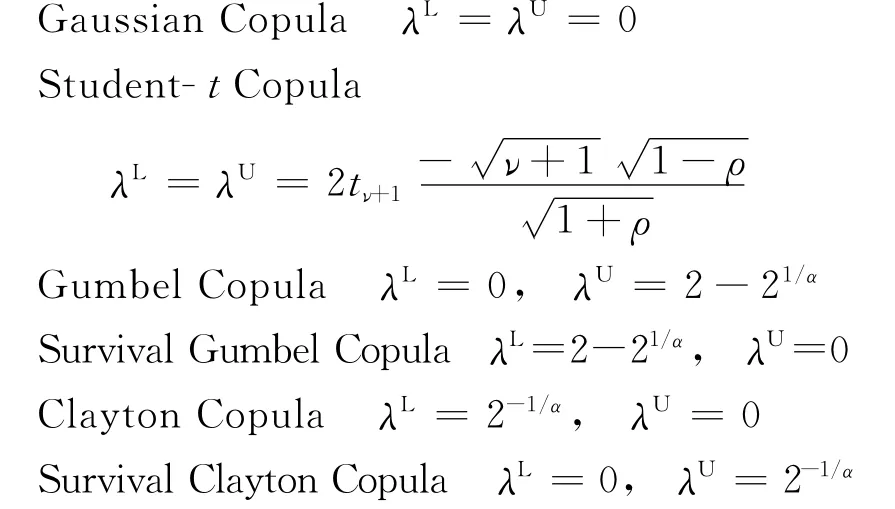
可见，Gaussian Copula不能描述尾部相关性，Student-tCopula能够描述对称的尾部相关性，Gumbel Copula和Survival Clayton Copula能够描述上尾相关性，但不能描述下尾相关性，Survival Gumbel Copula和Clayton Copula能够描述下尾相关性，但不能描述上尾相关性。

考虑到连续波动率变量可能同时存在下尾和上尾相关性，且呈现非对称特征，因此，引入能同时捕获下尾和上尾相关性的SJC（Symmetrized Joe Clayton）Copula。SJC Copula[15]通 过 对“BB7”Copula（也称为Joe-Clayton Copula）[23]进行修正后得到。SJC Copula允许非对称的下尾与上尾相关性，且包含对称的尾部相关性为一个特例。因此，它是一个非常灵活的Copula。SJC Copula的表达式为

当λL=λU时，SJC Copula是对称的。

另一种能同时捕获下尾和上尾相关性的Copula是混合Copula。构建如下两种混合Copula——Gumbel混 合Copula和Clayton混 合Copula：

式中：θ=（ω，α1，α2）′；CGum、CSG、CClay和CSC分别表示Gumbel Copula、Survival Gumbel Copula、Clayton Copula和Survival Clayton Copula函数；ω反映了具有下尾相关性的Copula（Survival Gumbel Copula和Clayton Copula）在混合Copula中的相对重要程度。对于Gumbel混合Copula，下尾和上尾相关性分别为：

对于Clayton混合Copula，下尾和上尾相关性分别为：

上述传统静态Copula假设相关性参数不随时间变化，不能捕获连续波动率变量间可能存在的尾部动态相关性，因此，需要将静态Copula模型扩展为动态Copula模型。本文采用动态Copula模型中的Markov机制转换Copula模型展开研究。在Copula函数中引入状态变量st，假设st=｛0，1｝服从一个一阶两状态的Markov过程，状态转移概率

设

由此，Copula参数随状态变量st的变化而变化，可以捕获波动率聚集的尾部动态性。

1.2 模型参数估计

本文采用半参数的两阶段估计法，即IFM（Inference Function for Margins）方法[23]来估计Markov机制转换Copula模型。第1阶段，对股票收益率的波动率的边际分布进行非参数估计；第2阶段，将估计的边际分布代入Copula函数中，估计出Copula参数。根据已有研究[23-24]，两阶段法是非常有效的估计方法，且在计算上容易处理。此外，半参数估计可以使边际分布免于设定误差，获得稳健的Copula参数估计结果[25-26]。

为了能够充分刻画股票收益率的波动率的“偏斜”“尖峰厚尾”等经验特征事实，本文采用非参数方法来估计边际分布函数F（x）。具体地，根据重标度的经验累积分布函数估计得到边际分布函数：

式中，1｛·｝为示性函数。经验累积分布函数重标度是为了确保Copula对数似然函数的一阶条件对所有有穷的T有定义。根据Glivenko-Cantelli定理，一致收敛于真实的经验累积分布函数F（x）。

在Markov机制转换Copula模型中，待估计的参数向量给定波动率的经验累积分布函数的非参数估计，运用极大似然方法获得Markov机制转换Copula模型参数的估计为

式中：⊙为Hadamard乘积；初始值设为无条件概率（遍历概率），即

2 实证研究

本文采用上证综合（SSE）指数和深证成份（SZSE）指数日内5 min高频交易价格数据作为研究样本。数据抽样的时间跨度为2010-01-04～2015-12-31，两指数均有69 600个日内观测值。所有数据均来源于天软数据库。

众所周知，波动率不能从金融市场中直接观测得到。基于此，本文采用日内高频交易数据构建已实现波动率作为隐波动率的代理变量。第t交易日已实现波动率定义为

式中：n为日内收益率总数目；rt，i=100（lnPt，ilnP t，i-1）为t交易日的第i个日内（对数）收益率。研究表明[27]，在理想的市场条件下（不存在市场微观结构噪声、资产可连续交易以及资产价格不存在跳跃），已实现波动率RV依概率收敛于积分波动率（Integrated Volatility，IV），即

式中，σ2（t）为波动率过程。

式（18）计算的已实现波动率RV忽略了重要的隔夜信息，实际应用中往往低估真实波动率。为了克服该问题，Hansen等[28]引入“隔夜效应”，构建了如下修正的已实现波动率：

式中，rt，0=100（lnPt-1，n-lnPt，0）为隔夜收益率，

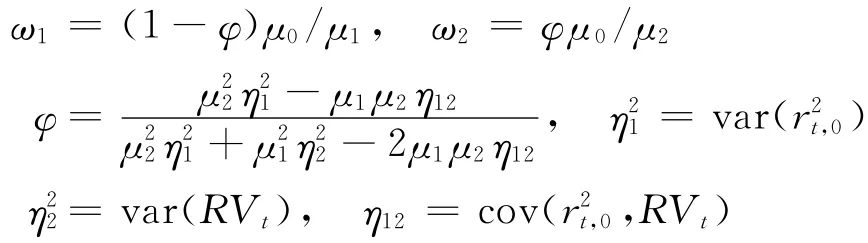
μ0、μ1和μ2分别为（r2t，0+RV t）、r2t，0和RV t的均值。研究表明[28]，修正的已实现波动率RV*是真实波动率的一个非常有效的代理指标。鉴于此，本文运用式（20）来构建已实现波动率，并以此作为隐波动率的代理变量。

图1为SSE和SZSE指数已实现波动率序列。

图1 SSE和SZSE指数已实现波动率序列图

表1给出两指数已实现波动率的描述性统计量。由表1可见，两指数已实现波动率均呈现正偏（偏度＞0），且存在尖峰、厚尾特征（峰度＞3），也都拒绝正态分布的假定（Jarque-Bera统计量显著）。

根据式（11）计算得到已实现波动率的边际分布，进而采用极大似然方法得到各Copula的参数估计结果，如表2所示。由表2可见，所有Copula的相关性参数估计值均在统计上显著，表明沪深股市波动率聚集存在线性或非线性相关性。由Gaussian Copula和Student-tCopula的估计结果可见，沪市波动率聚集（线性）相关性约为0.75，深市波动率聚集（线性）相关性约为0.7，沪市相比深市呈现更为明显的波动率聚集性特征。比较Gaussian Copula和Student-tCopula的估计结果，发现Student-tCopula具有更大的对数似然值和更小的AIC值，表明能描述尾部相关性的Student-tCopula具有更好的拟合效果以及沪深股市波动率聚集尾部相关性的存在。基于AIC信息准则，能同时描述下尾和上尾相关性，且允许非对称的下尾和上尾相关性的SJC Copula在所有Copula中具有最好的拟合效果。由SJC Copula的估计结果可见，上尾相关性参数估计值相比下尾相关性参数估计值明显更大，表明高波动率的聚集相比低波动率的聚集发生概率要更高，沪深股市波动率聚集具有尾部非对称特征。

表1 描述性统计量

表2 Copu1a参数估计结果

对波动率聚集非对称性的一种解释是信息到达率[29]，即波动率聚集来源于信息到达在时间上的聚集。在金融市场中，极端的与平稳的时期在时间上是聚集的。在极端的金融市场危机时期，股票市场波动率较高，信息到达速度快、频率高，从而导致更高的高波动率聚集的可能性。而在平稳时期，股票市场波动率较低，信息到达速度慢、频率低，从而导致更低的低波动率聚集的可能性。

为了捕获沪深股市波动率聚集可能存在的尾部动态特征，选择Copula为具有最优拟合效果的SJC Copula，构建相应的Markov机制转换Copula模型进行分析。运用极大似然参数估计方法，得到模型的参数估计结果，如表3所示。由表3可见，基于AIC信息准则，引入机制转换后，SJC Copula模型的拟合能力有较大提高。在st=0下，沪深股市波动率聚集的下尾相关性分别为0.215 8和0.148 0，上尾相关性分别为0.760 9和0.634 0；在st=1下，沪深股市波动率聚集的下尾相关性分别为0.496 7和0.653 8，上尾相关性分别为0.537 5和0.470 0。无论是st=0或st=1，沪市上尾相关性均明显大于下尾相关性。深市在st=0下，上尾相关性明显大于下尾相关性；但在st=1下，下尾相关性明显大于上尾相关性。采用Hamilton[30]算法，计算得到沪深股市波动率聚集滤过的下尾和上尾部动态过程：

如图2、3所示。由图2、3可见，沪深股市波动率聚集确实呈现明显的尾部动态特征。

表3 Markov机制转换SJC Copu1a模型参数估计结果

图2 SSE指数波动率聚集的下、上尾部动态相关性

图3 SZSE指数波动率聚集的下、上尾部动态相关性

3 结语

波动率聚集性是金融资产收益率序列中的一个重要特征，也是金融领域关注的重要问题。通过对波动率聚集性的研究有助于加深对金融市场微观结构的了解，对资产组合配置、风险管理及期权定价都具有重要意义。本文构建了Markov机制转换Copula模型来研究中国股票市场的波动率聚集性（波动率相关性结构）。采用上证综合指数和深证成份指数日内高频数据，构造已实现波动率作为隐波动率的代理变量，对中国股票市场进行了实证分析。结果表明，SJC Copula函数相比其他Copula函数能更好地刻画中国股票市场的波动率聚集性，波动率聚集具有明显的尾部非对称特征，高波动率的聚集相比低波动率的聚集发生概率要更高。波动率聚集非对称性表明，股票市场中坏时刻的聚集相比好时刻的聚集更频繁，金融市场动荡相比平稳具有更高的可能性。另外，基于Markov机制转换SJC Copula模型的研究表明，中国股票市场的波动率聚集还展现出明显的尾部动态特征。