基于双时间尺度扩展卡尔曼粒子滤波算法的电池组单体荷电状态估计

刘征宇 汤 伟 王雪松 黎盼春

1.合肥工业大学机械工程学院，合肥，230009

2.安全关键工业测控技术教育部工程研究中心，合肥，230009

0 引言

电池荷电状态（state-of-charge，SOC）估算对于电动汽车意义重大。目前常用的SOC估计算法主要有电流积分法［1］、放电试验法、开路电压法、负载电压法、电化学阻抗谱法、内阻法、神经网络法和基于电池模型的卡尔曼滤波算法［2-3］以及状态观测器方法［4］等。近年来，出现了自适应无迹卡尔曼滤 波［5］（adaptive unscented Kalman filter，AUKF）、鲁棒卡尔曼滤波［6］（robust extended Kalman filter，REKF）等改进的卡尔曼滤波算法，以及改进的观测器算法，包括H∞观测器算法［7］、自适应Luenberger观测器算法［8］及 PI观测器算法［9］等。但以上方法主要研究如何对单个电池进行精确的SOC估计，而实际应用中电池组中电池单体由于制造工艺的不一致和使用环境的不一致，或多或少会导致单体间SOC的不一致［10］。在电池组单体SOC不一致时，如果使用以上方法则只能对电池组单体SOC进行逐个估计，从而导致计算复杂度太高。

针对电池组各单体的SOC估算问题，文献［11］首先提出了一种将单体SOC分为电池组平均SOC和各单体差异SOC，并对平均SOC和差异SOC分别进行估算，最终将得到的平均SOC值与差异SOC值相加，即可得到各单体SOC值。这种方法相对于逐个对电池组单体SOC进行估计的方法，很大程度上简化了计算复杂度。但是该文献没有提出具体的算法流程，实用性较差。文献［12］基于一个筛选过程来实现电池组各单体间的一致性，但在实际使用过程中，电池组单体不一致性会逐渐显现，只能解决电池组单体初期的SOC估算问题。文献［13］首先建立分频模型，然后采用奇异值分解（singular value decomposition，SVD）来简化求解。该方法能对电池组单体SOC进行精确估计，但其精确估计范围较小。

粒子滤波技术［14］基于统计学来解决模型中非线性引起的误差，但粒子滤波算法可能会出现粒子不足的现象，且对模型依赖性强。扩展卡尔曼粒子滤波（extended Kalman particle filter，EKPF）算法利用扩展卡尔曼滤波（EKF）算法对每个粒子进行更新，将最后得到的近似后验密度作为重要密度函数，并将最新观测值引入，可降低粒子退化的概率，进而提高粒子滤波算法的估计精度［15］。

为实现对电池组各单体在实际应用中全SOC范围内的SOC精确估计，本文选用锂电池作为研究对象。首先根据锂电池增强自校正（enhance self correcting，ESC）模型推导出电池组平均模型和各单体的差异模型，然后根据EKPF算法实现对电池组平均状态和各单体差异状态的精确估算，并且为了降低计算复杂度，设计了基于双时间尺度EKPF的电池组单体SOC估计流程。

1 电池组平均模型与各单体差异模型

对单体锂电池进行建模，得到相应的ESC模型［16］如图1所示，该模型能较全面地体现锂电池的动态特性。

使用等效电路模型来描述锂电池组单体电池的工作特性，其中，Ek代表电池k时刻的开路电压；hk代表电池k时刻的迟滞电压；yk为k时刻的负载电压；R0为电池的欧姆内阻；R1、R2为极化内阻；C1、C2为模拟电池极化的电容；ik为k时刻的放电电流。模型使用了两个RC电路环节，来模拟电池的极化效应。

本文对串联锂电池组进行研究。由于电池组中的单体电池是串联的，所以所有单体的电流相等，均为ik。电池单体放电时电流积分法离散形式如下：

图1 ESC模型Fig.1 ESC model

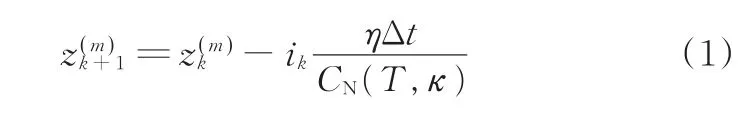
由式（1）得到SOC平均状态方程：

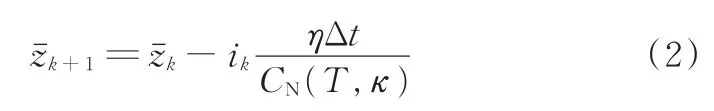
式中，zˉk为电池组所有单体在k时刻的SOC均值。

对于锂电池模型，根据基尔霍夫电压定律和基尔霍夫电流定律，有

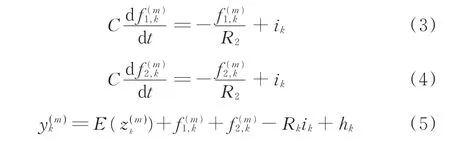
离散化式（3）、式（4）得

锂电池迟滞电压离散形式如下：

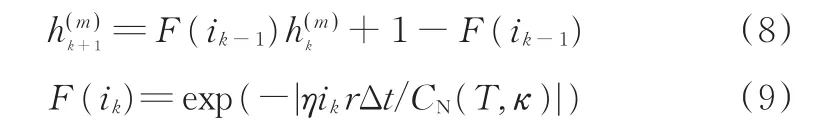
式中，r为调整衰减速率。

由式（8）可得平均迟滞电压

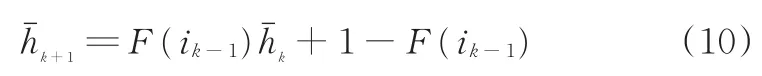
由式（6）、式（7）可得平均极化电压状态方程：

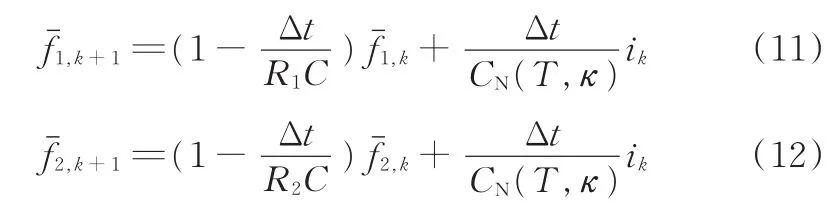
（1）电池组平均模型。由式（2）、式（10）～式（12）得到电池组平均状态方程：

对应的观测方程为

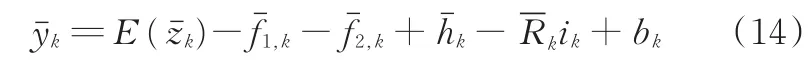
（2）单体差异模型。各单体电池的差异SOC值定义如下：

差异SOC值状态方程为

对应的观测方程为

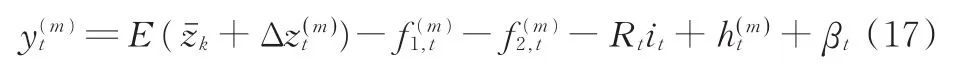
式中,αt为单体电池模型中的系统噪声；βt为单体电池模型中的观测噪声，它们均为高斯白噪声。

2 基于EKPF的电池组单体SOC估计算法

由于电池组平均模型和各单体差异模型的观测方程是非线性的，故为实现对各单体差异状态和电池组平均状态的精确估计，本文选用EKPF算法对锂电池组平均SOC值和各单体差异SOC值进行估计。

非线性系统如下：

式中,xp为p时刻系统的状态矢量；yp为p时刻系统的观测值；f(xp)、g(xp)为非线性函数；wp、vp分别为系统噪声及观测噪声，它们均为高斯白噪声，wp～N(0,Q)，vp～N(0,R);Q为系统噪声方差；R为观测噪声方差。

EKPF算法步骤如下：

（1）根据初始概率分布P（x0）产生N个粒子样本，i=1,2,…,N，N个粒子之间的协方差定义为

对于电池组平均模型，根据式（13）得EKF算法中的状态转移矩阵为

其EKF算法中的测量矩阵为

对于电池组第m个单体差异模型，其EKF算法中的状态转移值At=1，其EKF算法中的测量矩阵为

（3）更新权重，权重归一化。由测量结果yˆp计算粒子的后验概率：

对于电池组平均模型，观测噪声方差R为bk的方差，对于电池组单体，R为βt的方差。对权重归一化得

若Neff＜Nthreshold（Nthreshold为粒子数阈值），则进行重采样，重采样后的权重为1 N。

（5）求解p时刻状态的后验概率估计：

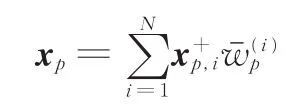
（4）计算有效粒子数目Neff：

（6）p←p+1，返回步骤（2）。

3 基于双时间尺度EKPF的锂电池组单体SOC估计流程

图2 双时间尺度EKPF算法流程图Fig.2 Dual time-scale EKPF algorithm flow chart

如图2所示，估算开始时先估算第1个单体差异SOC值和此时的电池组平均SOC值。估算完后再继续估算下一个单体的差异SOC值和此时的电池组平均SOC值，直至所有单体的差异SOC值估算完成。当对电池组各单体全部估算完成后，继续进行下一次估算。当估算到第m个单体时，其时间尺度关系如下：

k=Mt+m

当完成一次对所有单体的估算时，得到每个单体的差异SOC值和M个时刻的平均SOC值。最终根据下式得到各个单体在这M个时刻的SOC值：

通过双时间尺度的算法可实现对估算资源的合理利用，降低计算复杂度。

4 实验

为验证本文中算法的可靠性，对12节锂电池串联组成的电池组在变电流工况下进行实验，电池单体额定电压为3.2 V。放电电流如图3所示，在恒温25℃条件下放电5.1 h。模型参数以及算法初始参数如表1所示。

图3 放电电流随时间分布情况Fig.3 Discharge current distribution over time

表1 参数初值Tab.1 Parameter initial value

将通过采用安时计量法得到的SOC值作为本文SOC估计的参照标准。实验中，电池组平均模型粒子数设为200，差异模型粒子数设为50。电池组平均模型系统噪声和观测噪声的方差分别取10-8、10-5；电池组差异模型系统噪声和观测噪声的方差分别取10-10、10-8。根据本文双时间尺度EKPF算法得到各单体的SOC估算值如图4、图5所示。

图4 1至6号电池在双时间尺度EKPF算法下的SOC估算情况Fig.4 The SOC of cell 1～6 in dual time-scale EKPF algorithm

图5 7至12号电池在双时间尺度EKPF算法下的SOC估算情况Fig.5 The SOC of cell 7～12 in dual time-scale EKPF algorithm

将本文中的EKPF算法换成EKF算法，采用双时间尺度EKF算法对电池组各单体SOC进行估算，同时采用基于ESC模型的EKF算法对电池组各单体进行逐个估算，并将以上估算方法估算结果与双时间尺度EKPF算法进行比较。为对估算误差进行定量分析，首先定义均方误差

式中，e(m)为第m个单体的均方根误差；Te为实验中对第m个单体估算的总次数；为对第m个单体第i次根据积分法所得的SOC参考值为第i次对第m个单体估算得到的SOC估计值。

对12节单体电池采用双时间尺度EKPF和采用双时间尺度EKF的估算误差进行定量分析，得均方误差结果如图6所示。

由图6可知，双时间尺度EKPF算法能有效对电池组单体SOC进行估算，且采用双时间尺度EKPF算法比采用双时间尺度EKF算法和EKF算法对SOC估计的均方根误差小，说明了EKPF算法有效修正了模型的非线性误差，进一步提高了电池组单体SOC估算精度。

图6 12节电池单体的SOC估算均方误差Fig.6 Mean square error of the 12 cell SOC estimation

5 结语

本文首先对锂电池组单体进行建模，根据模型得出电池组SOC平均模型和各单体SOC差异模型，并针对电池组SOC平均模型和各单体SOC差异模型设计了具体的双时间尺度EKPF算法及具体的算法流程，最后根据算法流程对12节电池单体进行了实验。实验结果表明，双时间尺度EKPF算法能有效估计电池组各单体SOC，且相对于双时间尺度EKF算法和EKF算法具有更高的电池组单体SOC估算精度。

今后，可对EKPF中粒子数的选择进行细化研究，在满足电池组单体SOC估计精度要求的同时，选择合适的粒子数以尽可能降低计算复杂度。另外，新能源汽车电池管理系统中，SOC估算常受到噪声干扰，研究如何在噪声干扰情况下，克服因噪声干扰造成的电池组单体SOC估计精度下降问题将是未来研究的难点。