履带车辆混合驱动系统自动化建模

邹 渊 武金龙 田 野 孙逢春

北京理工大学机械与车辆学院，北京，100081

0 引言

低油耗、高供电能力以及低红外静默行驶要求使得履带车辆驱动系统电气化日益得到重视，尤其是混合驱动系统，研究者越来越多［1-3］。混联式混合驱动系统由于工作模式灵活、系统效率和部件性能综合优化空间大而成为近年来的研究热点［4-6］。混联式履带车辆属于多流传动系统，一般包含多个动力源，如内燃机和多个电动机/发电机，以及功率耦合和汇流装置。功率耦合装置负责内燃机和电动机/发电机的功率耦合，汇流装置则把直驶路和转向路的功率汇流后输出至侧传动装置。

功率耦合装置与汇流装置多采用行星轮系，行星齿轮机构的太阳轮、齿圈和行星架与发动机、电动机/发电机及输出轴有多种连接方式。若耦合装置含有多个行星排，则各行星排的自由端之间存在多种连接方式，使得系统结构复杂多样，获得系统层面最优的混合驱动系结构和参数是总体设计的难点。如何提高设计效率，科学而快速地获得较优的驱动系构型方案具有重要的理论和应用价值，而自动化建模技术有望解决上述问题。已有学者提出基于键合图、图论和超图的自动化建模方法［7-9］，实现了驱动系统的自动化建模，该建模过程存在结构—图—数学模型的两次转换，影响了建模效率。LIU等［10-11］和ZHANG等［12］提出了基于矩阵方程的自动化建模方法并将其应用在轮式混合动力车辆上。本文基于该方法的思路，提出适用于履带车辆混联式混合驱动系统的自动化建模方法，确定模型矩阵的生成和筛选规则，并通过系统构型方案优选实现其应用验证。

1 履带车辆混合驱动系统建模

图1所示为典型的多功率流混联履带车辆混合驱动系统，含有内燃机、两个电动机/发电机、转向电机、功率耦合装置和汇流装置。图1中，ωout、Tout为耦合装置输出端的角速度和转矩；K1为功率耦合装置和汇流装置间的传动比；K3为侧减速器到履带的传动比。

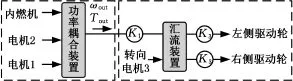
图1 混联式履带车辆混合驱动系统的结构简图Fig.1 Schematic structure of the powertrain of the power-split hybrid tracked vehicle

1.1 功率耦合装置建模

图2所示为履带车辆混合驱动系统双行星排功率耦合装置，S、R、C分别表示太阳轮、齿圈、行星架。

图2 某双行星排功率耦合装置Fig.2 Two planetary gear power coupling device

分别对与发动机、电机1、电机2和输出端相连的部分列写动力学方程：

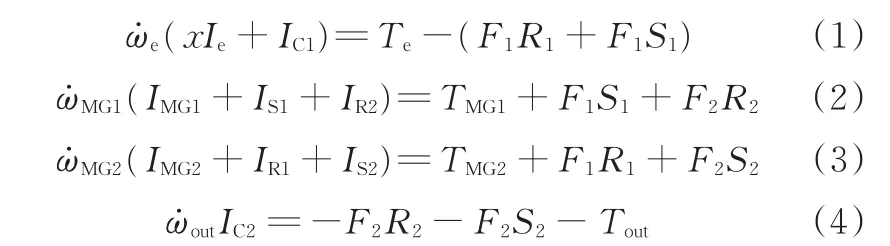
两个行星排运动约束方程为

对式（5）、式（6）求导后可得

另外有

式中，Ie、IMG1、IMG2为发动机、电机1和电机2的转动惯量；IS1、IR1和 IS2、IR2为耦合装置行星排 1、2的太阳轮、齿圈的转动惯量；IC1、IC2为耦合装置行星排1、2的行星轮和行星架的等效转动惯量；ωS1、ωR1、ωC1为行星排1的太阳轮、齿圈和行星架的角速度；ωS2、ωR2、ωC2为行星排2的太阳轮、齿圈和行星架的角速度；ωe为发动机的角速度；ωMG1、ωMG2为电机1、电机2的角速度；Te、TMG1、TMG2为发动机、电机1和电机2产生的转矩；S1、R1和S2、R2分别为耦合装置行星排1、2的太阳轮和齿圈与行星轮啮合时的节圆半径，标准啮合时等于分度圆半径；F1、F2为耦合装置行星排1、2的轮齿啮合时的啮合力。

综合式（1）～式（4）和式（7）～式（12），将上述方程整理成矩阵方程形式如下：

式（13）即为该功率耦合装置的数学表达式。

1.2 汇流装置建模

图3所示为履带车辆汇流装置的具体构型，其中K2为锥齿轮机构的传动比。

图3 某种汇流装置Fig.3 Power coupling device of the tracked vehicle

与功率分流装置类似，建立汇流装置的模型如下：

式中，ωin、Tin为直齿输入到汇流装置的角速度和转矩；ωsteer_l、ωsteer_r为经锥齿轮机构输入到左右两侧汇流行星排的角速度；ωoutl、ωoutr为左右输出端处输出的角速度；ωMG3为转向电机3的角速度；ISl、IRl和ISr、IRr为左右汇流行星排的太阳轮和齿圈的转动惯量；ICl、ICr为左右汇流行星排的行星轮和行星架的等效转动惯量；IMG3为转向电机3的转动惯量；IVl、IVr为整车质量等效到左右两侧输出轴的转动惯量；IMG3为转向电机3 产生的转矩；Tvl、Tvr和Tfl、Tfr为履带车辆左右两侧输出轴上受到的制动转矩和车辆行驶时左右两侧履带受到的阻力等效到输出轴上的阻力矩；Sl、Rl和Sr、Rr为左右汇流行星排的太阳轮和齿圈与行星轮啮合时的节圆半径，标准啮合时等于分度圆半径；Fl、Fr为左右汇流行星排轮齿啮合时的啮合力。

结合式（14）～式（20），可将上述方程整理为如下的矩阵方程：

式（24）为汇流装置的数学模型表达式。式（13）、式（24）和式（21）～式（23）构成履带车辆混合驱动系统的数学模型。

2 履带车辆混合驱动系统的自动化建模

2.1 耦合装置与汇流装置系数矩阵的一般形式

将式（13）和式（24）的系数矩阵分块，表达为系数矩阵的一般形式：

式中，J(Js)为和转动惯量有关的对角矩阵；矩阵D(Ds)及其转置矩阵DT()为和行星排机构各节点间连接方式相关的矩阵。

J矩阵的每一行分别对应内燃机、电机1、电机2和输出端这四个外节点，而每一行中非零元素表示与该行对应节点相连的部分等效到该节点上的转动惯量。

D矩阵的行同样对应内燃机、电机1、电机2和输出端这四个外节点，它的列则代表行星排，第一列代表行星排1，第二列代表行星排2，以此类推。矩阵中非零元素则表示与内燃机、电机1、电机2和输出端节点中相连的行星排节点类型，其中，-S代表太阳轮节点，-R代表齿圈节点，R+S代表行星架节点。

Js矩阵的每一行分别对应汇流装置的四个外节点：直驶功率输入节点、左侧汇流排的转向功率输入节点、左右两侧汇流排的输出端节点；每一行非零元素则表示与该行对应的节点相连的部分等效到该节点处的转动惯量。

Ds矩阵的行同样分别对应汇流装置的四个外节点，它的列代表汇流行星排，第一列代表左侧行星排，第二列代表右侧行星排。矩阵中非零元素表示与汇流装置的直驶功率输入节点、左侧汇流排的转向功率输入节点、左右两侧汇流排的输出端节点相连的行星排节点类型，其中，-S代表太阳轮节点，-R代表齿圈节点，R+S代表行星架节点。

2.2 自动化建模的步骤

归纳系数矩阵的一般形式，确定某履带车辆混合驱动系统的数学模型，关键在于确定矩阵D(Ds)和矩阵J(Js)。履带车辆混合驱动系统自动化建模的步骤如下。

（1）确定D矩阵。D矩阵表明了耦合装置中各部件的连接方式，而DT矩阵则是耦合装置的运动约束矩阵，包含装置的运动学信息。D矩阵的生成规则如下：

规则1 D矩阵的列数等于耦合装置中行星排的个数。

规则2 D矩阵的行数等于其列数加2，且每一行对应一个外部节点，这里定义第1～4行对应的外部节点分别为内燃机节点、输出端节点、电动机/发电机1节点、电动机/发电机2节点；若行数大于4，则之后的行对应自由节点，所谓自由节点是没有与任何外节点相连接的行星排节点。

规则3 对于D矩阵中的非零元素，-Si对应太阳轮节点，-Ri对应齿圈节点，Si+Ri对应行星架节点，i表示第i个行星排；如D(1,1)=Ri+Si，表示内燃机节点与行星排1的行星架节点相连，又如D(4,2)=-S2表示电机2节点与行星排2的太阳轮节点相连。

规则4 把矩阵中剩下的空位补零。

（2）确定J矩阵。J矩阵是耦合装置的惯量矩阵，它的对角元素代表了与每一个外节点相连的部分等效到该节点的等效转动惯量的和。J矩阵的生成规则如下：

规则5 J矩阵是一个对角方阵，其大小等于D矩阵的行数。

规则6 J矩阵各行对角线上的元素等于各行对应的外节点所连接部分的转动惯量等效到该外节点处的和，与外节点相连的部分可以通过D矩阵来确定。

（3）确定Ds矩阵。Ds矩阵包含了汇流装置中各部件的连接信息，而DTs矩阵则是汇流装置的运动约束矩阵，它包含了机构的运动学信息。Ds矩阵的生成规则如下：

规则7 Ds矩阵是一个4×2的矩阵。它的第1列代表左侧行星排，第2列代表右侧行星排；它的1～4行分别对应行星排连接的直驶功率输入节点、左侧汇流排的转向功率输入节点、左侧行星排的输出端节点、右侧行星排的输出端节点。

规则8 对于Ds矩阵中不为零的元素，-S代表太阳轮节点，-R代表齿圈节点，R+S代表行星架节点。但要注意，Ds(2,2)中的元素为其正常形式的相反数。如Ds(2,2)的正常形式为-Sr，表示右侧行星排的太阳轮节点与左侧汇流排的转向功率输入节点相连，但Ds(2,2)处的值应取其相反数，因此Ds(2,2)的正确形式为Ds(2,2)=Sr。

（4）确定Js矩阵。Js是汇流装置的惯量矩阵，它的对角元素代表了与每一个外部节点相连部分的等效转动惯量的和。Js矩阵的生成规则如下：

规则9 Js是一个4×4的对角方阵，其对角线上的元素等于各行对应的外节点所连接部分的转动惯量等效到该外节点处的和，与外节点相连的部分可以通过Ds矩阵来确定。

2.3 构型筛选条件

按照前文的D(Ds)矩阵和J(Js)矩阵的生成规则，可以穷举出给定系统行星排个数下的所有可能的矩阵形式，但这些矩阵所对应的系统构型并不都合理，还需要对构型进行筛选。由于模型中的D(Ds)矩阵包含了系统构型方案的所有信息，每一种构型确定的系统，都对应着一个形式确定的D(Ds)矩阵，且这种对应关系是唯一的，使得可以直接从D(Ds)矩阵的形式入手来对系统构型进行筛选。

下文以双行星排功率耦合装置及汇流装置为例，确定混合驱动系统构型的筛选条件。方便起见，把行星排机构等效为杠杆图（后文都采用杠杆图）：即一个行星排看作一根杠杆和杠杆上的三个点，三个点分别对应太阳轮（S）的自由端、齿圈（R）的自由端和行星架（C）的自由端，如图4所示。

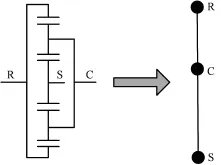
图4 单行星排杠杆图Fig.4 Single planetary lever diagram

2.3.1 物理可行性

筛选条件1①D矩阵的每一列中至少含有-S、-R、R+S三个元素中的两个；②每一列中不允许有重复的元素；③矩阵中至少有一列包含3个非零元素。

注意：若矩阵的某一列中只有两个非零元素，则缺少的那个非零元素对应的行星排节点被固定了。例如矩阵第1列中缺少-R元素，则表示第1个行星排的齿圈被固定了。

上面的条件①保证了每个行星排至少与2个外节点相连，也即至多只有一个节点接地固定，这就使得每个行星排至少有一个自由度；条件②保证了发动机、电机和输出端不会连接到同一个节点上；条件③使整个行星排耦合装置中至少存在一个起耦合作用的行星排，以保证装置的能量耦合功能。

筛选条件2D矩阵中任意一行的元素不能全为零。

这个条件限制了所有外节点必须至少与一个行星排节点相连。因为如果存在没有和行星排节点连接的外节点，那么说明内燃机、电机或输出端空置，失去了工程意义。

筛选条件3必须保证行星排装置的功率耦合功能。对于只含有两个非零元素的列，该列的前两个元素中必须有且只有一个元素非零。只有这样才能实现转速和转矩解耦下的功率耦合。

首先排除不满足转速解耦功能的构型：从构型的结构上看，表现为内燃机与输出端直接相连。“直接相连”除了指内燃机节点与输出端节点直接连接（这种情况已经在“筛选条件1”的条件②中排除）外，还指图5a所示的情况。图中输出端的转速与内燃机的转速成比例变化，不满足转速解耦的要求，筛选时必须排除。

然后排除不满足转矩解耦功能的构型：从构型的结构上看，表现为内燃机与输出端连接在同一个行星排上，而且除了这个行星排外二者不再与其他行星排相连（图5b）。图中内燃机和输出轴连到了同一个行星排上，根据行星排的转矩关系，易知输出轴转矩与内燃机转矩成确定的比例关系，因此不满足转矩解耦的要求，筛选时必须排除。

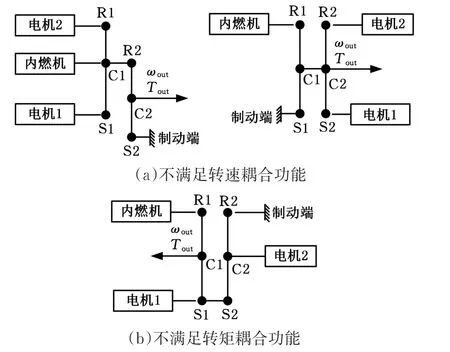
图5 不满足功率耦合功能的不合理构型举例Fig.5 Infeasible configuration without the function of the power coupling

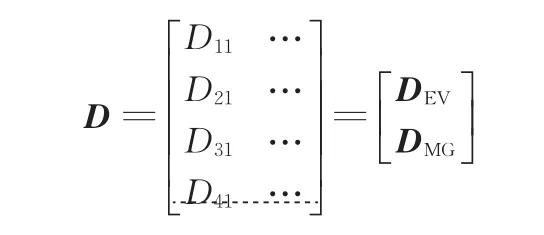
筛选条件4 矩阵DEV、DMG必须是满秩矩阵。

该条件保证了耦合装置的自由度数为2。其中DEV和DMG是D矩阵的子矩阵：

2.3.2 模式切换可行性

多行星排功率耦合装置常在内部加入离合器，通过离合器的接合与分离来实现系统不同工作模式。反映到D矩阵上，就是在其中添加或删除某些元素，得到的新矩阵即是原系统模式切换后所对应的矩阵：

因为矩阵的第二列只有两个非零元素且缺少的元素为-S2，说明第二个行星排的太阳轮固定。如果把行星排2的太阳轮节点与其他节点连接以实现装置的另一种工作模式，实际可以通过切换离合器来完成，而反映到D矩阵中，则是用-S2去替换矩阵第二例中的0元素，具有两种模式：

或

虽然矩阵形式上有两种模式，仍需要确认是否满足模式切换可行性。画出与上面矩阵对应耦合装置的结构如图6所示。

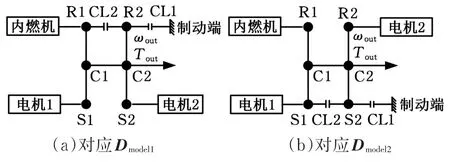
图6 两种双模系统的结构图Fig.6 Structure of two 2-mode system

对于图6a的构型，当系统工作模式要从D切换到Dmodel1时，由于切换前S2接地，太阳轮转速为0，按照挡位切换时主被动端转速应该同步原则，模式切换时要求内燃机的转速也为0，但当前内燃机技术实现这样的同步换挡操作不具备可行性，因此构型图6a不满足要求。而图6b中模式切换的离合器位于电机1处，图6b的构型能够实现同步换挡操作，是可行的构型。

分析可得：D矩阵第一行（发动机）和第二行（输出轴）中的0元素不能用其他元素（-R,-S,S+R）替换，反之亦然。即用于模式切换的离合器不允许和发动机轴或输出轴相连。由此有如下的筛选条件：

筛选条件5 对于两列均含有3个非零元素的D矩阵来说，矩阵前两行的所有元素不能全部非零。

筛选条件6 对于某一列只有2个非零元素的D矩阵来说，该列的前两个元素不能全为0。

上述自动化建模步骤和筛选条件可扩展并适用于三行星排及以上的耦合装置。

2.3.3 汇流装置的构型筛选条件

汇流装置要保证左右两侧连接方式的一致性，因此汇流装置的Ds矩阵具有固定的形式：

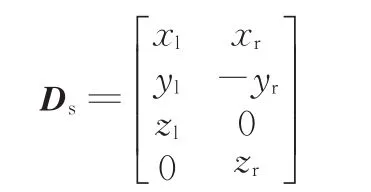
其中，x为 -S、-R或S+R；y为-S、-R或S+R；z为 -S、-R或S+R；且x、y、z各不相同。

式（25）是汇流装置的筛选条件，满足该形式的所有汇流装置构型都满足物理可行性的要求。

2.4 耦合装置与汇流装置模型矩阵的统一

耦合装置与汇流装置通过中间物理量ωout、Tout联系。在建立前向模型进行仿真时，中间量容易引起代数环，为了避免代数环，简化建模过程，把二者模型矩阵合成为统一化的模型矩阵，具体步骤如下：

（1）合成后的模型矩阵方程可以分块为如下结构：

式中，Dm为合成后的D矩阵；Jm为合成后的J矩阵；Ω̇m为合成后的加速度列向量；Fm为合成后的行星排内力列向量；Tm为合成后的外转矩列向量。

（2）Dm矩阵是一个(n+3)× n的矩阵，n为混合驱动系统中行星排的个数，n≥3。

（3）Dm矩阵可以表示为下面的分块矩阵：

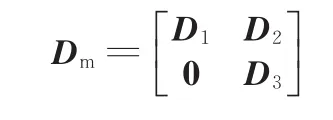
其中，D1为原耦合装置的D矩阵；D2为一个n×2矩阵，矩阵的第二行元素为Ds(1,∶)/K1，其余元素为0，n为混合驱动系统中行星排的个数，Ds(1,∶)表示原汇流装置的Ds矩阵的第一行元素，D3为原汇流装置Ds矩阵的后三行元素，即D3=Ds(2∶4,∶)。

（4）Jm矩阵是一个对角方阵，其大小等于合成后的D矩阵行数。

（5）Jm矩阵各行对角线上的元素等于该行对应的外节点所连接部分的转动惯量等效到该外节点处的和，与外节点相连的部分可以通过Dm矩阵来确定。

（6）对于n=4的情况，合成后的模型矩阵方程中的其他量为

2.5 矩阵方程的求解

统一模型矩阵方程（式（26））中，内力Fm实际上是中间量，出于运算效率的考虑，并不需要对它求解。依据相关数学推导［6］，得到消去Fm的矩阵方程的最终形式：

式（27）表明，对于任意结构的混联式履带车辆混合驱动系统，只要确定系统的D矩阵和Ds矩阵，依据统一模型矩阵的生成方法得到Dm矩阵和Jm矩阵，就可以得出系统的统一模型，实现混合驱动系的自动化建模。

3 自动化建模的验证

首先，采用后向仿真方法，通过对左右两侧履带输入运行工况，从而从后向前计算出驱动系统中三个电机的转速、转矩和功率。因此，可采用功率相等的方法进行验证，在整个系统中存在两个功率相等关系：①输入到汇流装置的功率应等于总需求功率；②电池组功率等于三个电机的合功率。如仿真结果满足两个功率相等的条件，说明模型计算功率与参考功率相等，即证明混合驱动系统模型的正确性。其次，用模型计算的电机转矩为输入进行前向仿真，通过输出车速与转向角速度分别与参考值的对比，进一步验证模型的正确性。

3.1 混合驱动系统构型

以图2和图3组合形成的系统为例对模型进行验证，履带车辆参数如表1所示。其中D矩阵和Ds矩阵如下：

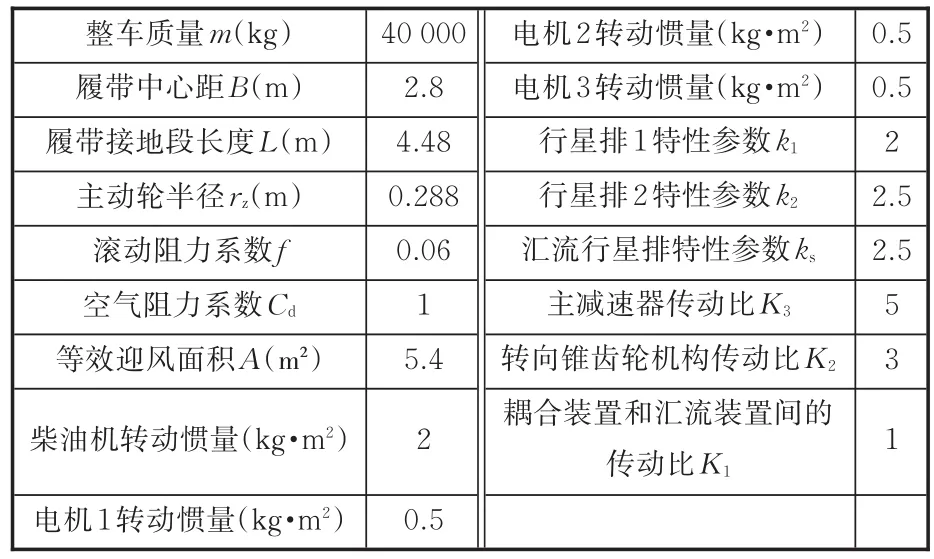
表1 履带车辆及其驱动系统参数Tab.1 Parameters of tracked vehicle and its powertrain

3.2 仿真结果

利用自动化建模方法对上述系统建立后向仿真模型并进行求解，即据式（27）依据两侧履带速度和加速度来求解力矩输入。图7为仿真所用的工况，图7a为直驶工况，图7b为转向工况。直驶工况来自某履带车辆实车场地试验，转向工况包括了中心转向、小半径、中等和大半径转向工况，它们构成了履带车辆典型行驶工况。

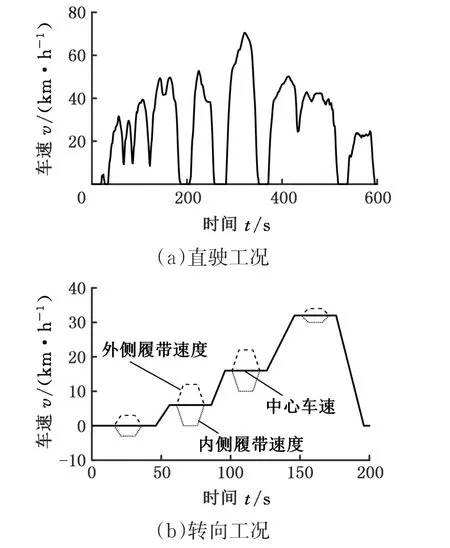
图7 仿真工况Fig.7 Driving schedule for simulation

图8显示了直驶工况下总功率、电功率及其误差情况，可以看出，输入汇流装置的总功率与总需求功率基本相等，最大相差0.1 kW；电池组功率与三个电机功率之和基本相等，最大相差0.75 kW。图9显示了转向工况下总功率、电功率及其误差情况，最大相差分别约为0.19 kW和0.75 kW。

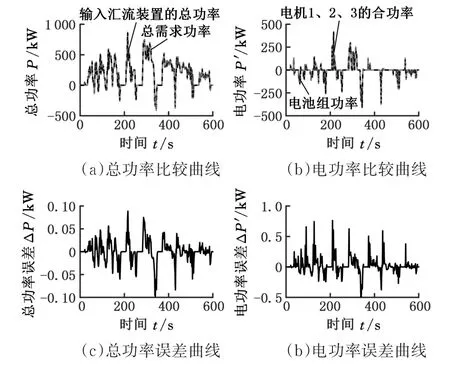
图8 直驶工况下的总功率、电功率及其误差曲线Fig.8 Total and electric power and error in straight forward driving

采用前向仿真模式，根据式（27），输入为以上后向模型计算出的各部件转矩，输出为车速和转向角速度，直驶和转向仿真结果分别如图10和图11所示。该图显示前向模型的仿真结果与参考工况完全符合。

图9 转向工况下的总功率、电功率及其误差曲线Fig.9 Toal and electric power and error in steering

图10 直驶工况下的车速仿真结果Fig.10 Vehicle speeds and error in straight forward driving

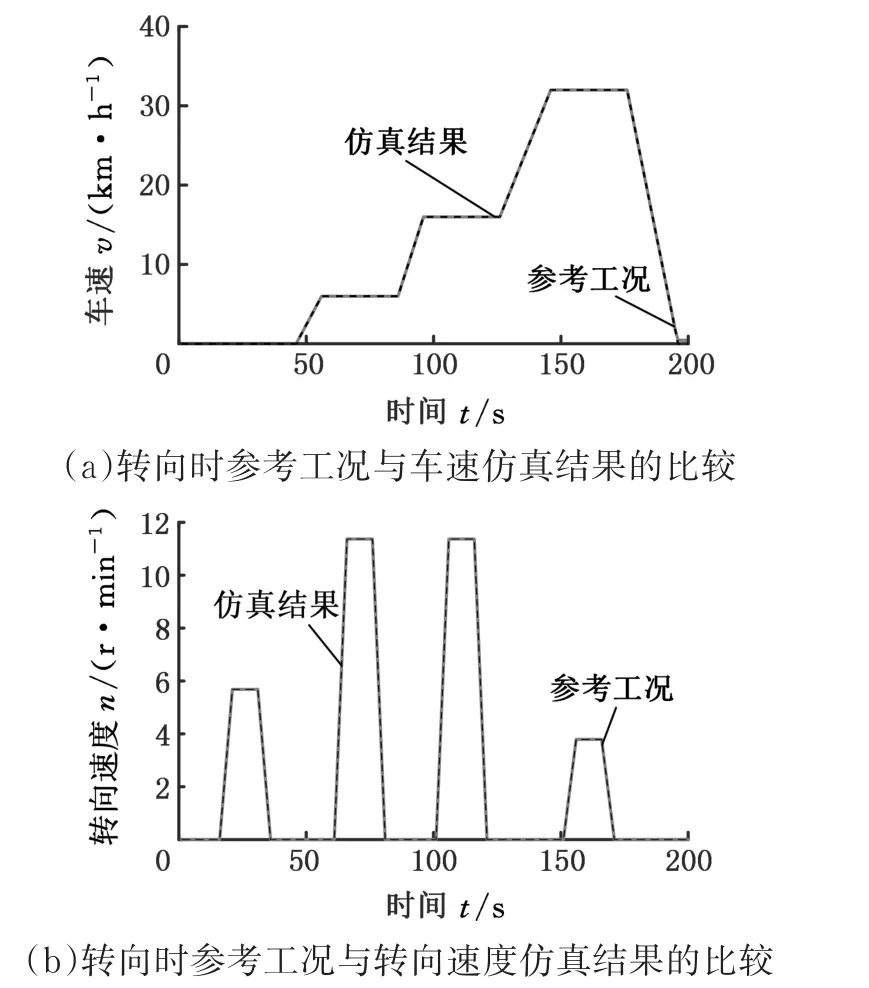
图11 转向工况下的仿真结果Fig.11 Simulation result in steering

后向模型与前向模型仿真结果的一致性证明所提履带车辆混合驱动系统自动化建模方法是正确和有效的。

4 采用自动化建模方法的构型优选

利用自动化建模方法对履带车辆混合驱动系统的所有可能构型进行穷举，并经过优选可得所有合理系统构型及其数学模型。

4.1 优选条件

机动性是系统的优先筛选条件，驱动系应能首先满足工况行驶需求。优选时以图7工况为输入，采用后向仿真模型对系统构型和参数进行计算，得到系统部件（包括发动机和电动机）需要输出的转速、转矩和功率参数。相同机动性能下参数值较小的系统即为较优系统。本文选择电机1和电机2的功率值作为评价参数。

4.2 优选策略

依据2.2节中所述自动化建模规则，通过修改D和Ds矩阵的参数来遍历动力部件与行星排不同连接。排除电机转速或转矩过大的构型。即电机转速、转矩满足如下约束：

式中，ωmax1、ωmax2、ωmax3分别为电机1、2、3所能提供的最大角速度；Tmax1、Tmax2、Tmax3分别为电机1、2、3所能提供的最大转矩，由设计者提前确定。

满足上述条件的构型中，分别计算电机1和电机2的功率绝对值的平均值（考虑到发电时电机功率为负值），最后比较平均功率的大小，取该值较小的构型为较优构型。图12为构型优选策略流程图。

图12 构型优选策略流程图Fig.12 Optimal screening diagram of hybrid powertrain architecture

4.3 优选结果

以含有4个行星排机构的履带车辆混合驱动系统（即耦合装置两个行星排，汇流装置两个行星排）为例，编写系统构型的生成、筛选和优选程序，仿真工况如图7所示，参数设置见表1。表2是程序的运行结果，只列出了排在前15位的构型编号。

表2 按电机平均功率从小到大排列的模型矩阵编号Tab.2 Model Matrix ranking based on average power of electric motors

通过观察发现，对于（3×3）形式的构型，第27号构型和第42号构型为较优构型；对于（3×2）形式的构型，可观察到第34号构型和第81号构型为较优构型。从结果中提取这四个构型的模型矩阵，观察后发现（3×2）形式的34号构型其实就是（3×3）形式的27号构型经过模式变换后的构型。表3和图13分别是构型的模型矩阵及其结构杠杆图。

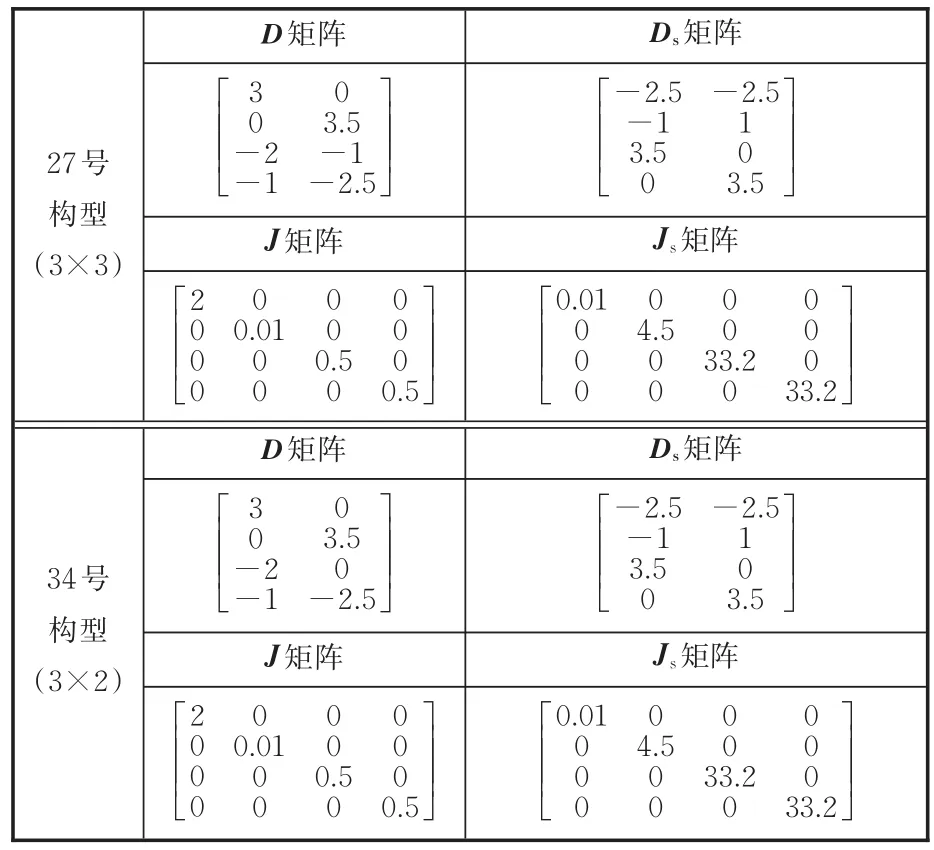
表3 较优构型的模型矩阵Tab.3 Model matrix of the optimal architecture

图13 较优构型的杠杆简图Fig.13 Lever diagram of the optimal architecture

图13中当离合器CL1接合，CL2断开，得到的构型就是（3×3）形式的27号构型；当离合器CL1断开，CL2接合，得到的就是（3×2）形式的34号构型。该耦合装置方案构型与通用汽车公司在2003年提出的一种双行星排结构的混合动力系统方案［7］较为相似，见图14。二者的不同在于通用汽车公司方案的离合器位于电机2处，该方案处于模式1时，行星排1的太阳轮和行星排2的齿圈接合，此时系统结构与耦合装置的模式1（CL1接合，CL2断开）完全相同；模式2时，行星排1的太阳轮和行星排2的齿圈断开，而行星排2的齿圈接地（制动）。

图14 美国通用汽车公司的一种双行星排混合动力系统方案Fig.14 A two-planetary gear hybrid powertrain from General Motor US

图15 模式1（CL1接合，CL2断开）下较优构型的仿真结果Fig.15 Simulation result of the oprinal configuration in mode 1（CL1 engaged and CL2 disengaged）

由于较优构型与图14所示专利构型在模式1下构型完全相同，所以在相同循环工况下部件工作点的仿真结果完全相同，如图15所示。模式2时专利构型所需电动机1和电动机2的功率远大于优化所得构型的功率需求。图16显示，在车速较高的情况下，图14专利构型的模式2会导致两个电机的转速非常大，而图13构型则不会出现这种情况。因此本文优选出的构型在模式2上的性能要优于图14所示专利构型的性能。

图16 模式2（CL1断开，CL2接合）下较优构型的仿真结果Fig.16 Simulation result of the oprinal configuration in mode 2（CL1 disengaged and CL2 engaged）

5 结论

（1）提出了一种适用于混联式履带车辆混合驱动系统的自动化建模方法。先以耦合装置与汇流装置的建模为例，推导了自动化建模的方程，基于此总结出自动化建模的步骤，并针对构型本身和模式切换的可行性，提出了可用构型的筛选条件。通过前向和后向模型仿真验证，证明了所提的自动化建模方法的正确性和有效性。

（2）编制了自动化建模程序，以系统构型的优选为实例开展自动化建模的应用，得到了4行星排机构的履带车辆混合驱动系统的较优构型，并将其与通用汽车构型进行对比分析，证明了其优选性。

（3）本文所提方法实现了履带车辆混合驱动系统的自动化建模与优选，提高了系统的设计与建模效率。所建系统模型可直接应用于混合动力履带车辆驱动系统的仿真计算、参数匹配及优化控制等。