基于水库-河道耦合关系的水库水沙联合调度模型研究与应用

谈广鸣，郜国明，，王远见，李新杰

（1.武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072；2.黄河水利科学研究院 水利部黄河泥沙重点实验室，河南 郑州 450003）

1 研究背景

在多沙河流上修建的水库改变了天然河道水流结构与河床形态自然平衡状态，造成水库泥沙的淤积，而水库调度的运用又会影响下游河道河床的演变［1］。因此在水库调度中，不仅需要调节径流，满足防洪发电生活生态用水需求，还需要调节泥沙减少水库淤积，同时还要考虑出库泥沙在下游河道的淤积分布和淤积效益。因此，如何实现水库调度、水库淤积和下游河道河床演变相互协调的水沙联合调度，成为研究的难点问题［2-3］。

自1974年三门峡水库采用“蓄清排浑、调水调沙”运用方式以来，国内学者开始对多沙河流的水库开展了水沙联合调度的研究［4］；杜殿勖等［5］构建了考虑供水、发电、潼关高程为约束条件的下游河道淤积量最小为目标函数的水库水沙联调随机动态规划模型；包为民等［6］将异重流总流微分模型引入到多沙河流水库中，描述水库泥沙的运动过程，探讨了以出库排沙比最大为目标的水沙联合调度问题；练继建等［7］建立了适于不同目标和预案的异重流过程梯级水库联合调度模型；吴巍等［8］运用水沙数学模型与优化调度理论，构建了多沙河流水库水沙联合优化调度耦合模型；晋健等［9］构建了基于SBED扩散一维全沙水库冲淤计算的水库水沙联合调度模型；彭杨等［10-11］基于水库蓄水和排沙的矛盾，构建了以水库防洪、发电及航运调度为子模块的水沙联合调度多目标决策模型；白涛等［12］建立了以输沙量、发电量最大的单目标模型及多目标水沙调度模型。以上成果分别从不同方面对水沙联合调度问题进行了研究，但由于多沙河流水库水沙条件的不确定性，使得各研究成果均局限于某一特定问题，且过去的单向优化调度计算仅考虑水库调度对下游河床演变的影响，未能将维持下游河道中水河槽目标与水库蓄水排沙的响应关系反馈到水库水沙联合优化调度模型中。要使水库调度实现真正的优化，就必须建立包含下游河道恢复中水河槽目标在内的多目标水库优化调度模型，让河道响应的结果实时反馈到目标函数和水沙优化计算中，实现水沙过程的全定义域寻优和下游河道河床演变结果的动态反馈。

本文基于水沙数学模型与优化理论的基本思想，以水库防洪、减淤发电及生态供水为基本目标，应用多目标决策方法，集成了发电效益、水库减淤效益、下游河道河床演变等多个计算子模块，构建兼顾下游河道整治需求与水库综合效益的多沙河流水库多目标优化调度的数学模型，实现了水库-河道动态耦合，完成水库调度随河道响应状态的实时优化，并将该模型应用于小浪底水库优化调度研究中，研究水库的多目标优化调度及下游河道河床演变规律，探讨多泥沙河流水库群水沙联合调度机制。

2 基于水库-河道耦合的水沙联合调度模型

图1 水库-河道耦合的水沙联合调度模型计算流程

本文通过发电效益、水库减淤效益、下游河道河床演变3个计算子模块的耦合构建了联系水库和河道的水沙联调模型。其计算流程如图1所示。由图1可知，水库的来水来沙条件和下游河道边界共同构成了多沙水库调度的外部约束条件，而水库本身的调度能力和兴利需求共同决定了水库的职能和调度目标。现阶段对水库多目标调度的处理方式通常有3种［13］：（1）将部分目标转化为约束；（2）将原本不可公度的多目标采用数学方式处理后权重相加；（3）采用Pareto最优曲面的方法来表达最优解群。本模型中，将水库调度的供水、生态等效益都作为约束条件处理；而对水库的发电效益和库区减淤效益，则先将其转化成可量度的经济性指标，再相加作为目标函数；而对下游河道河床演变的结果处理最为复杂，一方面将其年度计算结果作为约束条件，如果满足则调度寻优成功，如不满足则调度寻优计算继续；另一方面在约束条件满足后，该年度计算结果又通过实时反馈，更新了下一年度水库优化调度计算的下游河道边界条件，这就构成了完整的水库-河道耦合的水沙联合调度模型。

2.1 水库水沙联合优化调度模型实现水库综合效益最大化是水库优化调度的基础，因此，本文分时段以发电量最大、库区淤积量最小，实现下游河道维持中水河槽为最优目标，以水库防洪（包括防凌）、供水、灌溉、除害兴利等需求作为约束条件，采用确定性的动态规划模型构建水库多目标优化调度模块。其目标函数形式为：

式中：F为综合效益函数；a、b为权重；ΔV为水库累积淤积库容，m3。

其中，洪水过程的各个时段作为阶段变量，时段初到时段末的水位蓄水量作为决策变量，各个时段的水位作为状态变量，水库水量平衡方程作为状态转移方程，水量平衡关系如下：

式中：Vt为第t时段末库容，m3；Vt-1为第t-1时段末的平均库容，m3；为第t时段的平均入库流量，m3/s；为第t时段的平均出库流量，m3/s；Δt为t时段的计算时长。

其约束条件有：

（1）水位约束。为保证大坝安全，水库的水位不应骤升骤降，在一定时段内，库水位应在某个确定范围内变化。在每年的汛期来临之前，水库应预留出一定的防洪库容，将库水位降至汛限水位以下，以满足防洪要求。即水库水位应满足：

式中：为在t时段内水库可能的最低运行水位，m；为t时段内水库达到的最高运行水位，m；Zt为t时段内任一时刻水库水位，m。

（2）下泄流量约束。水库下泄流量的下限通常根据下游供水和生态需水的需要综合确定，上限由下游汛期防洪安全要求确定。各时段允许流量变动范围即水库下泄流量应满足：

式中：为t时段水库允许下泄的最小流量，m3/s；为t时段水库允许下泄的最大流量，m3/s；为qt为t时段水库内任一时刻的下泄流量，m3/s。

（3）出力约束。水库出力约束应满足：

式中：为t时段水库发电机组限制最小出力，104kW；为t时段水库发电机组限制最大出力，104kW；Nt为t时段内任一时刻的出力，104kW。

（4）非负约束。所有变量均为非负。

2.2 水库发电调度子模块水库的发电量是水库综合效益的基本指标，其计算函数形式为：式中：E为年度总发电量，kW·h；K为电站出力系数；为水库t时段内的过机流量，m3/s。由于

水库发电洞最大过机流量Qmax通常小于水库设计最大下泄流量，故{}；Hi为一年中

第t时段的坝前平均水位；m；H0为发电洞高程，m；Δt为每时段的计算时长。

2.3 水库泥沙冲淤模块

（1）库区淤积模块在本研究中，暂不考虑泥沙在库区的淤积形态对库区水沙输移的影响，而仅采用质量守恒方程计算库区泥沙淤积量，即：

式中：为第t时段的平均入库流量，m3/s；为第t时段的平均出库流量，m3/s；Δt为t时段的计算时长；ρ表示水库淤积泥沙的干容重，kg/m3。

（2）水库排沙模块水库排沙从大类上可分为壅水排沙、降水溯源冲刷和敞泄排沙3类［14］。在水库运用初期，水库水位不断抬升，此时壅水排沙情形较多出现；在库区淤积较严重而来水较丰的条件下，水库多采取降水溯源冲刷方式排沙；在水库达到冲淤平衡转入正常运用期后，则多采用敞泄排沙方式排沙。3种情况下，敞泄排沙的计算最为简单，即水库基本不拦沙：

当坝前水位较高，库区水深满足异重流潜入水深时，水库的排沙主要是壅水异重流排沙，泥沙沿程淤积，出库沙量一般小于入库沙量；当坝前水位较低，库区水深不满足异重流潜入水深时，此时水库的排沙主要是沿程冲刷、异重流排沙相结合或沿程冲刷、溯源冲刷、异重流排沙相结合［15］。其中，沿程冲刷采用式（9）计算［16］：

式中：G为沿程输沙率，t/s；J为库区内水面比降；B为库区内河道宽度，m；ψ为表征库区河床抗冲性能的系数，ψ=650表示河床质的抗冲性能最小，ψ=300表示中等抗冲性能，ψ=180表示抗冲性能最大。

异重流排沙采用式（10）计算［17］：

式中：S表示库区异重流输移到坝前下泄的含沙量，kg/m3；S0表示异重流潜入时的含沙量，kg/m3；Pl为异重流潜入断面级配百分数；α为饱和系数；l为粒径组号；ωl为第l组粒径沉速，m/s；L为异重流推进距离，m；q为异重流演进时库区内的单宽流量，m2/s。

异重流排沙有明确的潜入条件，与浑水运动的弗劳德数有关［18］。在本文算例中，已考虑了来水来沙条件是否能形成异重流条件，并由此选择相应的计算公式展开计算。马怀宝等［19-20］运用上述公式在计算2008年的小浪底水库异重流排沙时得到了理想的计算结果，验证了公式的合理性与适用性。

2.4 河道响应模块本模块着重关注在地貌学宏观尺度上下游河道对水沙过程的响应机制，以平滩流量作为下游河道排洪能力的表征，采用吴保生等［21-23］提出的滞后响应模型计算平滩流量的年际调整过程，该公式在黄河下游的河床演变中取得了较好的应用成果，因此选为河道响应模块的核心计算公式。

式中：Qbf为选定研究断面当年的平滩流量值，m3/s；Δσ为滞后时间，a；n为由当前年份向前倒推的滞后总年数；ξft为向前倒推t年的汛期平均来沙系数（来沙系数=含沙量/流量），kg·s/m6；Qfi为向前倒推t年的汛期平均流量，m3/s；ξf0为当年的汛期平均来沙系数，kg·s/m6；Qf0为当年的汛期平均流量，m3/s；K、β、b和c为待定系数。

需要特别指出的是，式（11）虽然只有流量和来沙系数两个变量，但来沙级配的影响是隐含在公式中待率定的参数滞后总年数n中，李凌云［24］的研究表明，衡量河道冲淤调整速度的参数M可表达为如下形式：

式中：h为河段平均水深；J为河段平均比降；C为悬沙浓度；d50为悬沙中值粒径。换句话说，来沙越粗，下游河床边界的调整越快，来沙越细，下游河床边界的调整越慢。因此下游河床的冲淤演变实际上是也同时受到了水库下泄流量、含沙量和泥沙级配的影响。

在本研究中，理想河床调整目标是作为约束条件出现的。修建多沙河流水库的重要目的之一即是为下游河道减淤，则长时段维持下游具有稳定排洪能力的主河道即为理想河床调整目标。如果当前河床尚未达到理想条件，则水库应持续拦截泥沙下泄清水，继续提升河道排洪能力；如果已达到理想条件，则水库可适当向下游河道排沙，在保证下游河道预期排洪能力的基础上，减少水库淤积库容，延长水库的使用周期。在本文中，用下游河道沿程监测水文横断面的平滩流量值来表征其排洪能力，其表达式为：

其中：Qi，bf表示第i个水文站点的断面平滩流量，m3/s；为水库下游河道主槽预期维持的平滩流量，m3/s。

2.5 模型求解如图1所述，本文采用动态规划和权重法对基于水库-河道耦合水沙联合调度模型进行求解［25］。由于水库的经济效益主要体现在发电效益和水库减淤效益（清淤成本）上，并且都可以体现在经济效益上，因此可对以上两个目标通过赋予权重转化成上述水沙联合调度多目标决策模型进行求解。而水库的防洪、灌溉、供水、生态效益和维持下游中水河槽通过流量、含沙量、泥沙级配约束的交集作为目标函数约束条件，这样，水库-河道耦合多目标水沙优化调度模型就可以转化成水库综合效益最大化的单目标非线性优化问题。

3 计算实例

3.1 小浪底水库概况小浪底水利枢纽是一座以“防洪（包括防凌）、减淤为主，兼顾供水、灌溉和发电，除害兴利，综合利用”为开发目标的枢纽工程，是黄河干流当前库容最大的控制性水利枢纽工程。总装机容量180万kW，多年平均设计发电量为51亿kW·h。小浪底年内调度一般分为三个阶段：第一阶段为上半年11月1日至下年汛前，该期间又可分为防凌、春灌蓄水期和春灌泄水期，期间水位变化不大；第二阶段为汛前调水调沙生产运行期，期间水位大幅下降；第三阶段为主汛期防洪运用、后汛期抬高水位蓄水。本研究针对2009年小浪底水库的调度过程展开，其对应的正常蓄水位为250 m，汛限水位为225 m，死水位为210 m。

3.2 结果与讨论以2009年小浪底水库实际调度过程为比对方案，采用本文构建的模型进行模拟计算。模型模拟计算小浪底水库2009年的流量过程见图2。

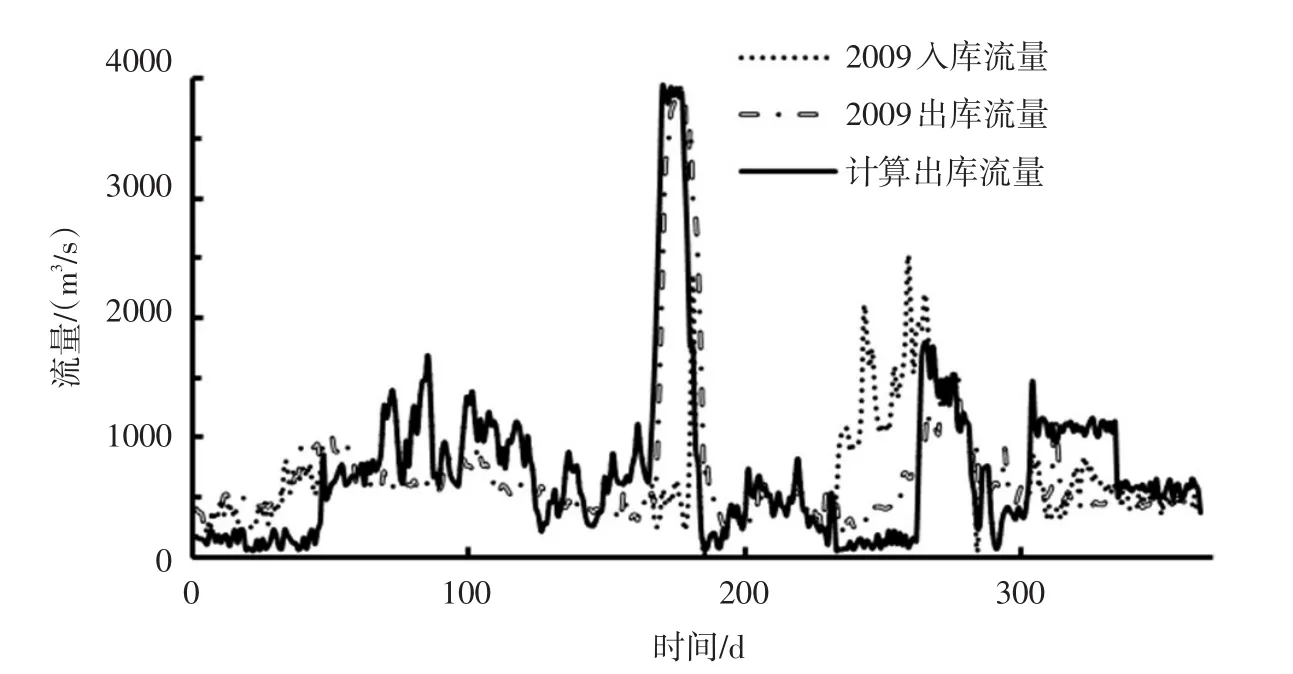
图2 小浪底水库2009年实测与模型计算流量过程

由图2可知，综合效益最大化的水库-河道耦合的水库水沙调度模型计算的小浪底出库流量过程与实际方案趋势一致，仍坚持塑造了一个大流量过程，以便于高效排沙的实现。不同之处在于，塑造的大流量过程时需打开排沙底孔，以长程异重流排沙的方式排沙出库，而不是将几乎所有泥沙全部淤积在库区内。

模拟调度方案的发电，库区减淤等综合效益如表1所示，可以看出，实际调度方案由于库区淤积量大的缘故［26］，最终的综合效益目标函数为-8.9亿元，即发电产生的效益不足以填补水库淤积造成的经济损失；而优化调度过程的发电量比实际调度过程发电效益增加了10%，淤积量减少近78%，排沙比增大，减小了库区的淤积。综合经济效益达到了11.86亿元，比实际调度增加了20.76亿元。

图3给出真实调度过程与综合效益最大的优化调度结果下黄河下游河道典型断面2009—2010年汛后平滩流量变化图。

由图3可知，对于真实调度过程，平滩流量的年度变化范围不大，花园口、孙口、艾山均有小幅冲刷，高村、利津河段有小幅回淤。利津站的平滩流量降至4000 m3/s以下。

表1 实测结果与理论模拟计算结果

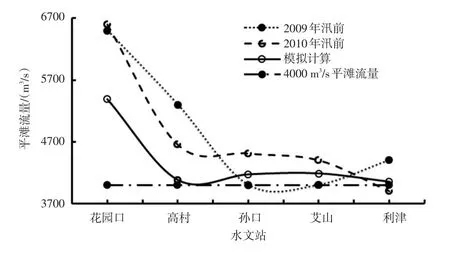
图3 黄河下游河道平滩流量对比

而模拟计算结果表明，黄河下游沿程平滩流量相比真实调度过程均有不同程度回淤，其回淤幅度从上到下逐渐减少，这也符合预期，即在花园口、高村这样平滩流量增大较多的河段可适当回淤，保持全河道过洪能力的平衡。

适当加大下泄沙量并没有导致黄河下游河道的严重淤积，尽管相比真实调度过程，模拟方案向下游多输送了1亿多吨泥沙，但由于尽可能利用了汛期的人造洪水，也增大了洪水在下游河道输移泥沙的能力，最终黄河下游淤积情况与实际调度方案相差不大，且各典型断面基本维持在4000 m3/s左右的平滩流量。

需要特别指出的是，本文虽然仅选取2009年一年作为算例，但事实上清晰体现了下游河床演变结果的反馈影响。因为造成本文的优化计算结果和实际调度方案之间效益巨大差异的原因就在于对下游河道河床演变结果的认识理念和处理方法上。实际调度方案中，由于没有考虑下游河床的现状相比1999年小浪底水库建成时已发生了巨大变化，而仍然坚持了清水下泄、冲刷下游河床的调度方式；优化调度方案则充分考虑了新的河床边界条件和维持下游中水河槽的目标，敢于加大下泄沙量，最终实现了库区-水库-河道效益的兼顾和多目标的优化。

4 结论

本文以水库发电、库区淤积、下游河道过流能力计算为基础，构建了兼顾水库综合效益和维持下游河道中水河槽的水沙多目标调度模型及求解方法，并以小浪底水库为研究对象进行了模拟计算，结果表明：（1）本文建立的模型实现了动态循环的水库-河道耦合计算，可将下游河道随水库调度发生的变化实时反馈到优化过程中来，实现更精细化的水库调度；（2）以小浪底水库2009年的水库调度方案为例，分析了该水库调度运行的各项边界条件，确定了其数学表达及临界阈值，给出了兼顾水库综合效益与下游减淤效益的综合效益最大的优化调度方案。计算结果表明，模拟方案相比真实调度方案，其发电量增加10%，而排沙比增至79%，下游河道维持了4000 m3/s左右的中水河槽。

因此，从科学角度，水库-河道耦合的水沙联合调度模型，在多沙河流的水库调度中能够有效兼顾库区-水库-河道效益，体现了该模型的合理性和适应性；从工程应用角度，利用好水库大流量排沙过程，在下游河道维持中水河槽的前提下适当排沙出库，延长多沙河流水库的使用寿命，从本研究看是完全可能的，现有的小浪底水库调度方案仍有进一步提升的潜力。