四参数随机生成法重构土体微观孔隙结构的分形特征

张季如，钟思维

（武汉理工大学 土木工程与建筑学院，湖北 武汉 430070）

1 研究背景

土的孔隙结构状况直接影响土中水、气和溶质的运移特性。传统方法获取土体孔隙是实测土的密度和比重来计算孔隙率，或利用压汞法间接获得孔隙大小及分布，但缺点是对孔隙结构描述能力较差。随着图像处理技术的发展，利用土壤切片技术及高像素数码相机、扫描电镜（SEM）制备土壤切片数字图像，可定量研究土的孔隙结构。但土壤切片技术复杂，切片过程易破坏孔隙结构。近年来迅速发展的X射线断层扫描（CT）和核磁共振（NMR）技术，能够无损获得土体结构的三维数字图像，并通过数字图像技术对孔隙结构进行直接、定量的研究，但CT、NMR技术的大规模应用，目前受到成本高、分辨率低的限制。此外，目前与土体孔隙相关的试验研究都是在采集的小样本上进行的，由于土的非均质性和土体结构的空间变异性，其研究结果的代表性较差［1］。而通过对土体孔隙进行不同程度的简化，建立相关模型来模拟和定量表征土的孔隙结构，是研究土体孔隙结构特征的有效方法［2］。利用虚拟的模型演绎实验现象，可预测土的水力学性质并促进土体孔隙结构特征在多尺度上的研究。

在石油、地质、采矿、冶金、土木和水利工程等领域，迄今为止已经发展了多种模型用于多孔介质结构特征及其物理、化学和力学性质的研究，如重建介质模型、孔隙网络模型等重建类模型和统计模型、分形模型等间接类模型。在基于随机理论的重建类模型中，Wang等［3］提出了一种四参数随机生长算法（Quartet structure generation set，QSGS）生成多相多孔介质微观结构，其特点是与真实土体的微观结构相似且孔隙形态可控，可对任意尺度的多孔介质系统进行结构重建，具有良好的尺度扩展性，因而被许多学者用于模拟和表征岩土介质的孔隙结构，来研究其中的渗流和传热特性［4-8］。然而，QSGS算法生成的多孔介质与真实土体的比较，目前仅停留在孔隙形态相似的定性认知阶段，相关的定量研究，仅见申林方等［7］基于两点概率函数（土壤系统中任意选取两点同时属于孔隙相的概率）来描述具有相同孔隙率的QSGS模型与CT图像中的土体孔隙结构特征。由于土体孔隙结构复杂，仅用两点概率函数来比较孔隙结构特征，略显单一，尚需要更多的定量比较，相关的量化研究方法也要另辟蹊径。此外，QSGS模型参数对重构孔隙结构的影响和控制目前仍缺乏充分了解，模型应用过程中的参数选择比较盲目，需要为此提供科学依据。

QSGS模型能否真实反映实际土体孔隙的几何和拓扑特征，关键在于该模型对孔隙的大小、数量、形状及其空间分布状况的描述是否与实际土体一致。由于土体的多相性和不均匀性，使得在定量描述孔隙几何特征和揭示其分布规律等方面的研究极其复杂，用传统的几何学方法来描述孔隙结构已相当困难。众所周知，土体孔隙形态具有统计意义上的自相似性和尺度不变性，即分形特征，许多学者用分形方法来研究土体孔隙结构，一些分维数也被用来刻画具有多孔体系的土体断面结构。例如，Anderson等［9］利用土壤切片图像研究了描述二维空间孔隙分布特征的质量分维数Dm和孔隙边缘粗糙程度的表面分维数Ds，许多学者将Dm、Ds作为描述土体孔隙结构的重要指标，并揭示其与土壤结构状况、土壤性质等的关系［10-16］。因此，判断QSGS模型能否真实反映实际土体孔隙结构特征，一种可行的方法是利用分形理论在重建模型和实际土体之间架设起一座联系的桥梁，以分维数为评价指标，定量比较二者的分形特性。鉴于此，本文对不同固结压力下的软黏土样制备具有不同孔隙率的SEM图像，利用数字图像技术对QSGS算法生成的重建模型和SEM图像进行定量分析，对比研究QSGS模型和真实土体中的孔隙形态、大小、数量及其分布规律。在此基础上，基于分形方法和实测数据估算孔隙的Dm和Ds，研究QSGS模型与实际土体孔隙的分形特性，探索Dm、Ds在描述孔隙结构中的作用，揭示模型参数对QSGS算法生成的微观结构的影响，为合理选取模型参数提供科学依据。

2 材料及方法

2.1 SEM图像制备与分析方法对SEM图像中二维空间分布的土体孔隙，孔隙度P定义为图像中孔隙面积与整幅图像面积的比值。该指标从微观尺度上表征了土体孔隙状况，与土力学中宏观上的孔隙率（孔隙体积与总体积之比）含义有所不同。为了制备具有不同孔隙度的土体SEM图像，对原状软黏土进行固结试验，试样直径61.8 mm，高度20 mm。选择荷载等级σv=100、400、800 kPa的土样，经低温干燥及刀切法制备SEM试样［17］。SEM试验采用JSM-5610LV型扫描电镜。在每级荷载下的土样中各选择一幅代表性强的SEM图像作为分析对象。为使分析结果具有可比性，所选图像均放大1000倍，分析区域300×300 pixel，面积约95μm× 95 μm，分辨率0.1 μm pixel-1。

图1 不同孔隙度的土体二元SEM图像

采用Image-Pro Plus（IPP）软件及目视法将SEM灰度图像转换为黑白二元图像，并对二元SEM图像中孔隙的孔径、面积、数量等进行测量、统计和分类［18］。即利用IPP阈值设定功能，阈值调试过程中用目测方式将SEM的原始图像与分割图形相比较，对同一图像采用多人多次分别选取后取平均值，分析结果误差控制在10%以内，以获得最佳阈值［17］。如图1所示，分割后的二元SEM图像中，孔隙为白色，固体颗粒为黑色。利用IPP测得σv=100、400、800 kPa时SEM图像对应的孔隙度分别为P=0.317、0.276、0.213，可见随着固结压力的增大，土样逐渐压实，P随之减小。

2.2 QSGS算法的基本原理土的团聚体由细小的矿物颗粒经凝聚和胶结作用而形成，是一个渐进的过程，而QSGS算法的固相生长法则类似于土的团聚体形成过程。以土粒和孔隙二相构成的二维土体孔隙结构为例，若令土粒为生长相，孔隙为非生长相，构造区域的初始相全为孔隙，则构造过程如下：（1）在构造区内的每个网格节点上，以分布概率Pd随机分布固相生长核，在最终构造出的孔隙结构中，Pd不能大于土粒面积的百分比，即Pd≤1-P；（2）网格节点上的各生长核按照给定的方向生长概率Pi（i代表生长方向，i=1，2，…，8），从图2所示的四面八方，向周围相邻网格节点生长。若8个方向的生长概率P1～P8相同，则生成各向同性的孔隙结构；（3）重复步骤（2）直至孔隙面积达到给定的孔隙度P。

应指出的是，QSGS算法通过P、Pd、Pi、Ii（n，m）等4个参数来影响和控制多相多孔介质微观结构的生成［3］，其中Ii（n，m）为概率密度，表示在i方向上第n相在第m相上的生长概率，反映了各相之间的相互影响。对于土粒和孔隙二相构成的土体，只需采用P、Pd和Pi三个参数，即可获得表征土体孔隙结构的QSGS模型。为了调查QSGS模型能否真实反映实际土体孔隙结构特征，并研究模型参数对孔隙形态的影响，本文采用Matlab程序编写QSGS算法生成不同参数的模型供分析用。为了与SEM图像可资比较，QSGS模型设定的分析区域为300×300网格，P取值与SEM图像的P相对应，Pd、Pi取值见表1。

表1 QSGS模型的分析区域和参数取值

图2 生长核的8个生长方向

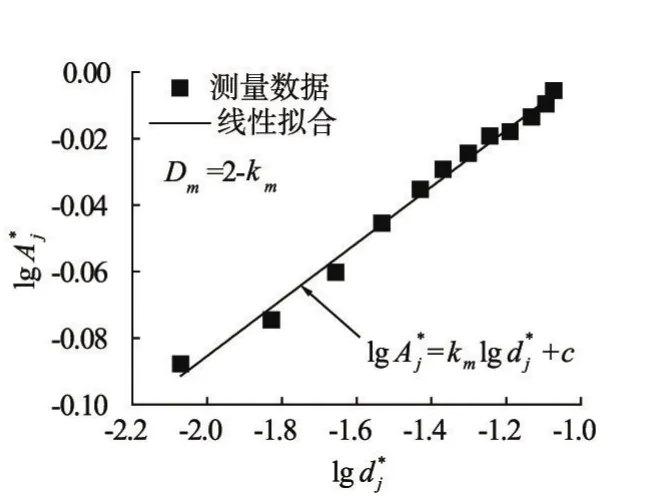
图3 质量分维数计算方法

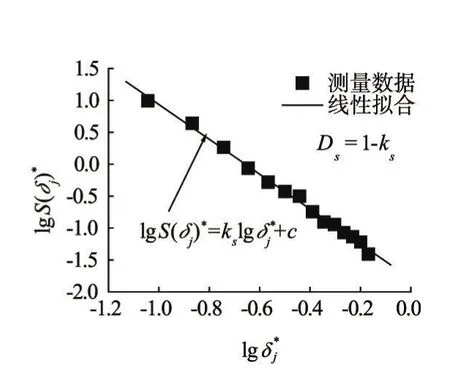
图4 表面分维数计算方法

2.3 质量分维数的计算方法土体孔隙在二维空间的分布方式可视为孔隙随机分布在土体截面上的分散系统，描述二维空间孔隙分布特征的质量分维数Dm，可采用增大分辨率并测定分散系统背景消失速率的方法来获得［11］。其原理是：设想在一系列不同放大倍数下观察SEM图像或QSGS模型（正方形截面）中的孔隙结构，首先在某个放大倍数下仅能分辨出最小孔径为d1的孔隙，并求得可见孔隙以外的剩余面积A（1正方形面积A与可见孔隙面积之差）。然后提高放大倍数，使能看到最小孔径为d2的孔隙，则剩余面积为A2。继续增大放大倍数，如此往复下去，使能看到最小孔径为dj的孔隙，相应的剩余面积为A（jj=1，2，…）。将dj和Aj进行标准化处理，获得标准化的孔径（实测孔径dj用正方形边长去除）和剩余面积（实测剩余面积Aj用A去除）。如图3所示，以为横坐标、为纵坐标点绘作图，若数据点有直线关系且斜率为km，则Dm=2-km。

2.4 表面分维数的计算方法基于构造步长技术，利用IPP扩展功能计算求得Ds。其原理是：利用IPP自动识别SEM图像或QSGS模型中的孔隙轮廓，并测量其最大Feret直径FD（孔隙轮廓断面在任意方向上投影的最大尺寸）。对孔隙轮廓选择一系列递减的标尺长度δ1、δ2、…、δj、…，自动测量一系列对应的孔隙轮廓周长S（δ1）、S（δ2）、…、S（δ）j、…，测得的孔隙轮廓周长将随δj值减小而增大。将实测δj、S（δ）j相对于FD进行标准化处理（用FD去除），如图4所示，这些标准化的和S(δj)*的对数值若能拟合成一条斜率为ks的直线，则Ds=1-ks。

3 结果与分析

模型参数P、Pd和Pi按表1取值，QSGS算法可生成由不同类型参数或参数取值不同组合而成的58种重建孔隙结构模型。限于篇幅，同时考虑到一些同类型参数组合的计算结果具有相同或相似的规律，本文仅以一些代表性组合为例，给出相应的计算结果并加以分析。

3.1 孔隙形态特征由于P表示孔隙所占的比例，因而反映了重建孔隙结构的疏密程度。图5为不同P在Pd=0.0001、Pi=0.001时QSGS算法生成的孔隙结构，直观显示了P的变化对重建结构状况的影响。P越大，重建结构松散，孔隙迂回曲折，存在连通与非连通孔隙。随着P减小，重建结构趋于密实。

图5 QSGQ算法生成的孔隙结构（Pd=0.0001，Pi=0.001）

Pd表示设定区域内网格节点成为生长核的概率，图6为不同Pd在P=0.276、Pi=0.01时QSGS算法生成的孔隙结构。可以发现，Pd较小时（Pd=0.0001～0.01），重建孔隙结构中的固相颗粒较大，孔隙大小和形状各异，分布不均匀，其孔隙形态与土壤结构最为相似，见图6（a）～（e）。随着Pd增大（Pd=0.05～0.1），重建结构中孔隙趋于微小，分布渐趋均匀，与土壤结构的差异增大，见图6（f）～（g）。当Pd取0.724的极限值（等于土粒面积百分比），则表明固相生长核不向周围生长，QSGS模型成为一种构造区内固相颗粒随机分布的简单模型，重建结构与土壤结构的差异十分显著，见图6（h）。

图6 QSGQ算法生成的孔隙结构（P=0.276，Pi=0.01）

Pi表示生长核在周围8个方向上的生长概率，图7为不同Pi在P=0.276、Pd=0.005时QSGS算法生成的孔隙结构。可以发现，不同Pi的重建结构的孔隙形态非常一致，并与土壤结构较为相似，表明不同Pi值对重建结构的孔隙形态影响较小。实际上，Pi反映了QSGS算法在重构计算过程中的迭代次数，Pi值越小，迭代次数越多。

由以上孔隙形态的定性分析，可知一些QSGS模型与土体的孔隙形态相似，模型参数对重建结构的影响也初见端倪。但QSGS模型对孔隙性质的描述是否与实际土体一致，还需要定量分析。

图7 QSGQ算法生成的孔隙结构（P=0.276，Pd=0.005）

3.2 孔隙分布规律将SEM图像和QSGS模型中的孔隙在其孔径范围内划分成12～16个孔径级别，d为每孔级对应的平均孔径。孔隙的孔径分布定义为小于各孔级d的孔隙所对应的孔隙度P（＜d），则孔径分布曲线为P（＜d）随d（对数）递增的变化曲线，见图8。将不同Pi在P=0.276、Pd=0.001生成的QSGS模型与土体的P（＜d）～d曲线相比较，见图8（a），可以发现，不同Pi值的QSGS模型P（＜d）～d曲线相互一致，并与土体P（＜d）～d曲线相吻合。同理，将不同Pd在P=0.276、Pi=0.005生成的QSGS模型与土体P（＜d）～d曲线相比较，见图8（b），不难发现，Pd=0.0001～0.01模型的P（＜d）～d曲线较为一致，并与土体P（＜d）～d曲线吻合较好，但Pd=0.05～0.724模型的P（＜d）～d曲线逐渐偏离了土体及Pd=0.0001～0.01模型的曲线，偏差趋势随Pd的增大而增大。

图8 孔径分布曲线（P=0.276）

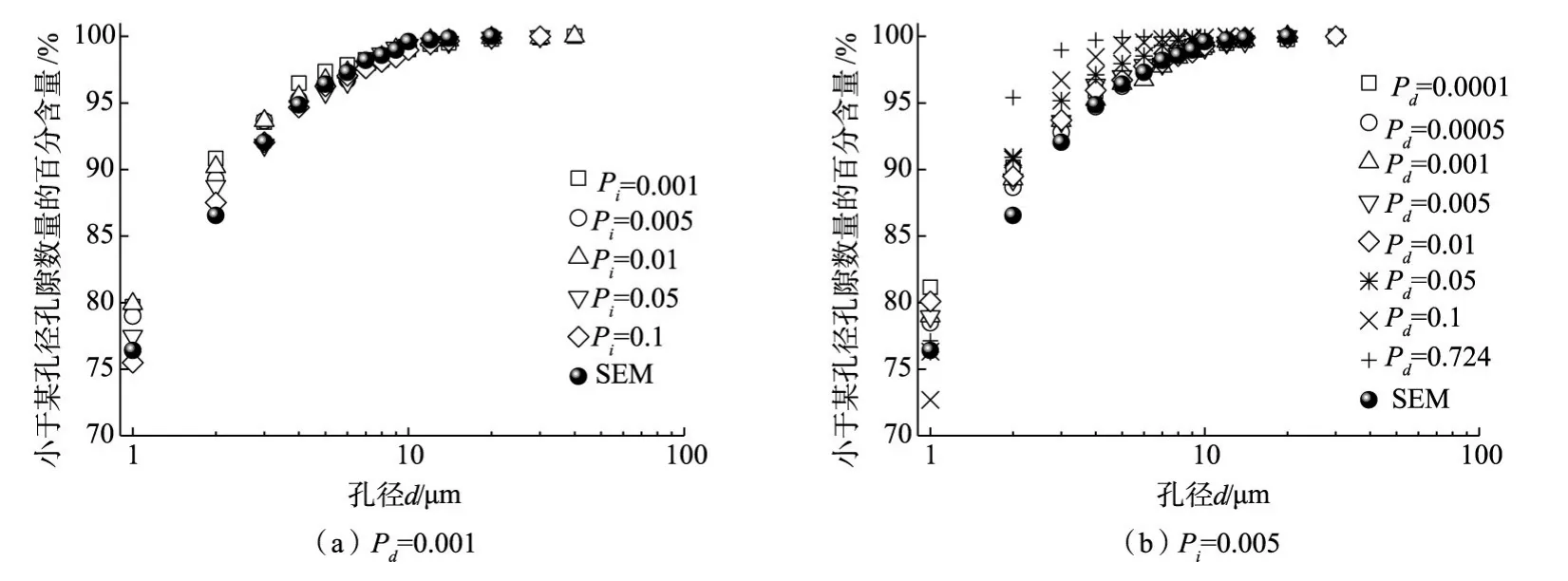
图9 孔隙数量分布曲线（P=0.276）

孔隙数量分布曲线定义为小于各孔级孔隙数量的百分含量随d（对数）的变化曲线，见图9。图9（a）为不同Pi在P=0.276、Pd=0.001生成的QSGS模型及土体的孔隙数量分布曲线。可以发现，与模型参数对P（＜d）～d曲线的影响规律相似，不同Pi值的QSGS模型与土体的孔隙数量分布曲线相吻合。图9（b）为不同Pd在P=0.276、Pi=0.005生成的QSGS模型与土体的孔隙数量分布曲线，可见Pd=0.0001～0.01模型的孔隙数量分布曲线趋向一致，且与土体的孔隙数量分布曲线吻合较好。Pd=0.05～0.724模型的孔隙数量分布曲线与土体和Pd=0.0001～0.01模型的曲线产生偏离，偏差程度随Pd的增大而增大。由以上分析可知，无论是P（＜d）～d曲线，还是孔隙的数量分布曲线，不同Pi的QSGS模型二种曲线相互一致，并与土体的二种曲线相吻合，说明参数Pi对重建结构的影响不明显。但参数Pd对重建结构的影响较为明显，Pd≤0.01模型的二种曲线相互一致，并与土体的二种曲线相吻合。

3.3 质量分维数由孔隙度的定义可知，当可看到标准化最小孔径为d*的孔隙时，相应的标准化剩余面积A*=1-P（≥d）。考虑P（≥d）=P-P（＜d），则A*=1-P+P（＜d）。将孔隙的测量数据标准化处理后，按照图3所示方法绘图并作线性回归分析，结果如下：（1）SEM图像和QSGS模型的测量数据均可拟合成一条直线。（2）对P分别为0.317、0.276和0.213的SEM图像，估算的Dm分别等于1.874、1.886和1.912，对应的拟合相关系数R2分别等于0.936、0.946和0.942。（3）对不同参数P、Pd和Pi的QSGS模型，获得的Dm值列于表2，对应的R2值随参数P、Pd和Pi的分布规律见图10。

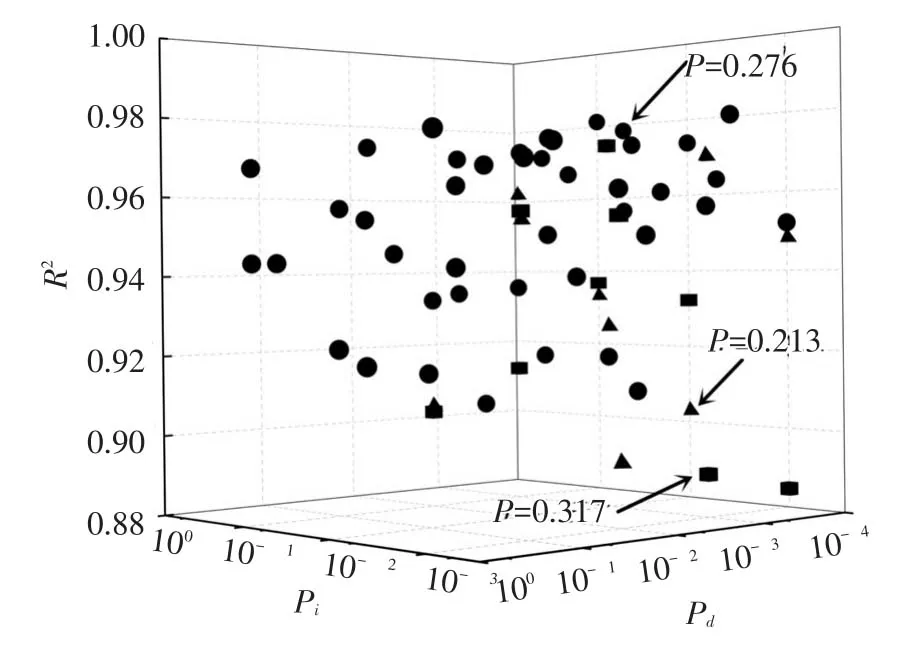
图10 拟合相关系数的分布规律

表2 不同参数QSGS模型的质量分维数Dm

对比SEM图像与QSGS模型的Dm值并结合R2值综合分析，考察实测数据与严格自相似分形特性的符合程度。表2数据显示，相同P的QSGS模型与SEM图像，二者Dm值较为一致。Pd对QSGS模型的Dm影响较为明显，Pi对模型的Dm影响不大。从图10可发现，无论SEM图像还是QSGS模型，总体上R2值在0.9以上，表明标化孔径d*与剩余面积A*线性相关的显著性水平较高，测量数据自相似性的显著性水平也较高，因而孔隙分布具有明显的分形特性。

为了深入了解模型参数对Dm的影响规律，图11绘制了P=0.276的QSGS模型在不同Pi时的Dm随Pd的变化规律。可以发现，Pd=0.0001～0.01模型的Dm随Pi变化较为稳定，Dm在1.883～1.907之间，平均Dm=1.897，与SEM图像的Dm（=1.886）较为吻合。Pd=0.05～0.724模型的Dm随Pi产生波动，Dm在1.791～1.881之间，平均Dm=1.834，明显低于SEM图像的Dm。

为了调查P对Dm值的影响规律，图12绘制了Pd=0.0001～0.01模型在不同Pi时的Dm随P的变化规律，并与SEM图像进行比较。可以发现，SEM图像的Dm随P增加而减小，拟合分析显示Dm～P呈线性变化规律，这一规律也在类似研究中得到证实［11］。QSGS模型的Dm随P的变化规律同SEM图像较为吻合，尽管Pi不同，总体上QSGS模型的Dm也显示了随P增加而减小的线性变化规律。

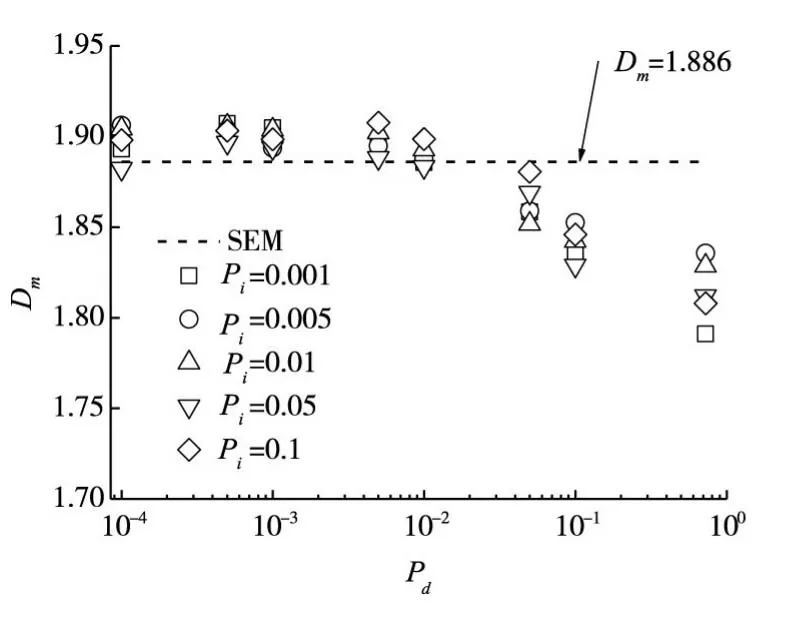
图11 Dm与Pd的关系（P=0.276）

图12 Dm与P的关系（P=0.276，Pd=0.0001～0.01）

从以上分析获得如下的认识：QSGS模型与SEM图像的孔隙结构均具有显著的自相似分形特性。QSGS模型的Dm对参数Pd较为敏感，Pd≤0.01模型与SEM图像的Dm数值大小基本吻合，并与P线性相关，能较好地表征土体的孔隙结构特征。

3.4 表面分维数限于篇幅，以相同孔隙度（P=0.276）的SEM图像和QSGS模型（Pd=0.0005、Pi=0.01）为样本，按照表面分维数的计算方法，算得二类样本中所有孔隙的Ds。图13给出了Ds的统计频数直方图。一般来说，Ds值的大小反映了孔隙轮廓线的曲折程度。孔隙轮廓边界愈粗糙，形状愈不规则，Ds愈大。图13显示：SEM图像的Ds在1.12～1.40之间，QSGS模型的Ds在1.14～1.42之间，二者的Ds取值范围非常接近，表明其孔隙轮廓边界的粗糙和曲折程度较为一致。

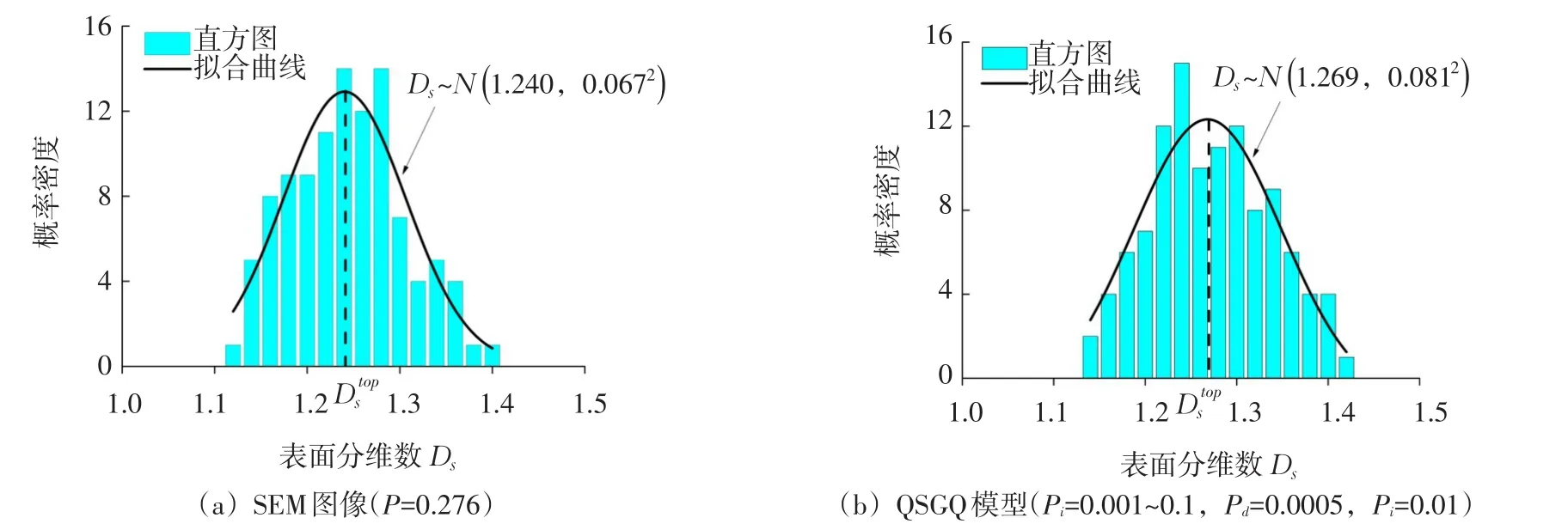
图13 孔隙表面分维数的统计频数直方图和正态分布拟合曲线

为了检验Ds是否符合正态分布，本文对含有不同孔隙度的3种SEM图像和不同参数组合的58种QSGS模型样本，利用SPSS软件中的K-S方法检验Ds是否符合正态分布，结果显示：K-S方法的p值在0.224～0.999之间，远大于0.05，说明这些Ds数据均来自于正态分布的总体，反映了土体和QSGS模型Ds分布的基本态势。如图13所示，直方图外廓线接近于正态分布拟合结果的概率密度曲线。将概率密度函数记为Ds～N（，σ2），其中曲线峰顶对应的Ds即为期望值，σ2为标准差。

由于Ds描述的是单个孔隙轮廓粗糙和曲折程度的指标，难以全面反映孔隙结构的整体不规则状况，应用时一般是将所有孔隙的Ds取平均值［16］。Ds频度正态分布曲线的期望值决定了曲线所处的位置，反映样本孔隙众数的Ds值。其标准差σ决定了Ds分布的幅度，即Ds的取值范围，故本文利用作为评价指标，能较为全面地反映孔隙结构的整体不规则程度［11］。

为了调查模型参数对的影响规律，图14给出了P=0.276的QSGS模型在不同Pi时的Dstop随Pd的变化规律。可以发现，Pd=0.0001～0.01模型的在1.232～1.262之间，平均=1.251，与SEM图像的（=1.240）较为接近，因而较好地反映了土体孔隙结构的整体不规则程度。而Pd=0.05～0.724模型的在1.252～1.366之间，平均=1.302，明显高于SEM图像的，因此所代表的孔隙结构整体不规则程度与实际土体差异较大。

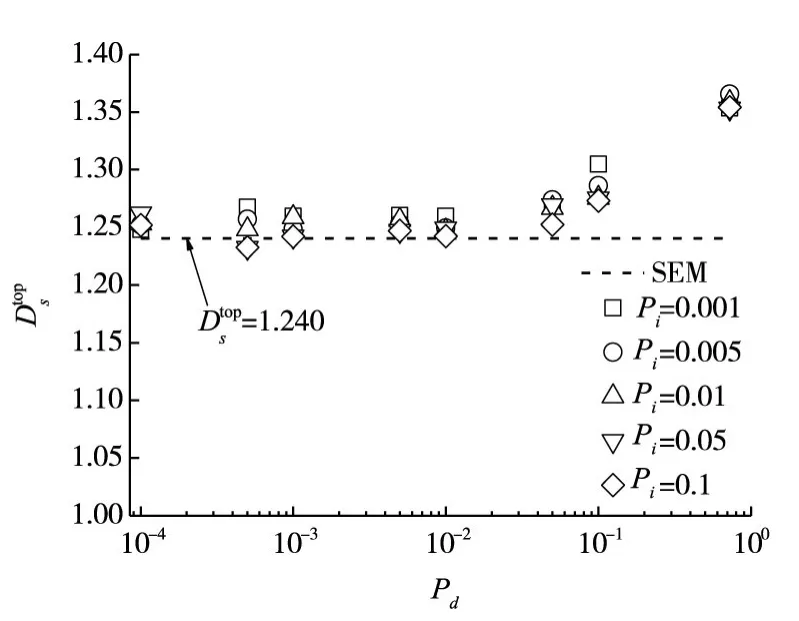
图14 与Pd的关系（P=0.276）

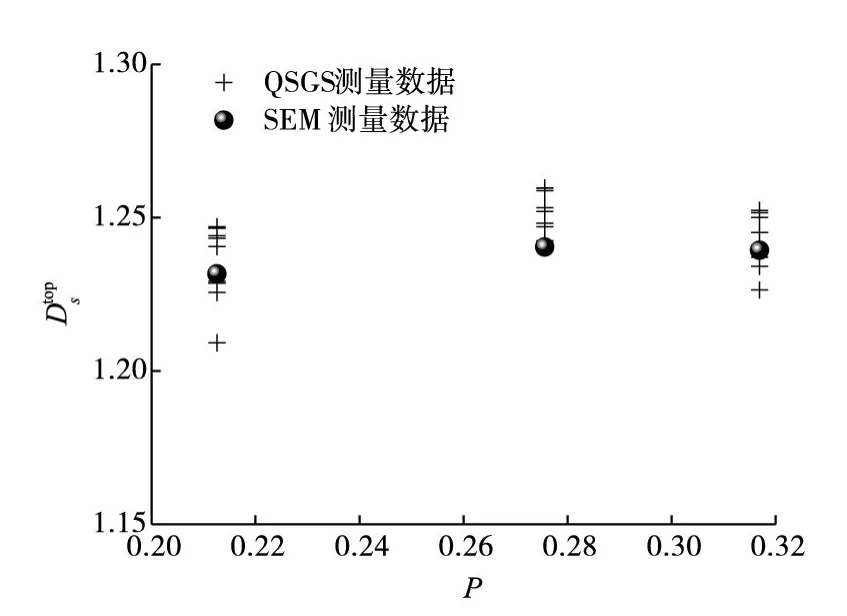
图15 与P的关系（Pi=0.001～0.1，Pd=0.0001～0.01）

为了调查P对的影响规律，图15绘制了Pd=0.0001～0.01模型在不同Pi时的随P的变化规律。可以发现，无论是QSGS模型或SEM图像，同一P值的值较为一致。总体上不受P值大小的影响，说明孔隙结构的整体不规则程度与孔隙度无关。

4 结论与建议

本文对三种不同孔隙率的土样制备SEM图像，旨在与QSGS模型进行定量对比分析。采用数字图像技术分析了QSGS模型与土体中的孔隙形态特征和分布规律，并估算孔隙的质量分维数Dm和表面分维数Ds。初步结论与建议如下：（1）QSGS算法生成的微观结构由P、Pd和Pi等参数控制，其中Pd对孔隙结构的影响更为显著。QSGS模型能否用于模拟和表征土体微观孔隙结构，取决于Pd取值是否合理；（2）在Pd≤0.01的取值范围，QSGS模型与土体的微观孔隙具有相似的形态特征、孔径分布和孔隙数量分布规律，以及较为显著的自相似分形特性；（3）QSGS模型与土体的Dm值较为吻合，P越小，Dm越大，Dm与P存在较为显著的线性回归关系，反映模型和土体在二维空间的孔隙分布特征相同；（4）QSGS模型与土体孔隙的Ds分布均表现为正态分布形式，Ds和期望值的大小较为一致，表明模型和土体在孔隙轮廓边界的曲折程度，以及孔隙结构的整体不规则程度上大致相同。

本文研究结果揭示了QSGS算法重构土体微观孔隙结构的分形特性，在一定程度上表明了QSGS模型的应用前景。然而，当QSGS模型用于预测土壤水力学性质时，应检验模型是否真实反映土壤孔隙结构状况，并在模型预测时采用合理的模型参数，以免造成预测结果产生较大的误差。