考虑投资者情绪的GARCH-改进神经网络期权定价模型

林焰，杨建辉

（1.华南理工大学 工商管理学院，广州 510640；2.北京大学 汇丰商学院，广东 深圳 518055）

期权作为一种经典的金融衍生品，在过去20年中创造出了巨大利润。期权产品可分为看涨期权与看跌期权，按照执行时间的不同又可划分为欧式期权、美式期权以及百慕大期权。期权赋予持有者买卖某种标的资产的权利，与远期合约与期货合约等其他金融衍生品相比，它不具有强制性，这一特性使得期权被广泛用于风险对冲、交易投机与套利。但如果对其管理不善，基于杠杆作用所放大的损失也是巨大的。期权作为市场上交易的主要金融衍生品，准确地预测期权价格将有助于投资者制定决策并降低风险。

1 问题描述

传统的期权定价方法依赖于参数化模型。Black等[1]基于Black-Scholes微分方程（B-S 微分方程）提出了第1个完整的期权定价公式，奠定了期权定价理论研究的基础。但Black-Scholes欧式期权定价模型（B-S模型）所基于的一系列假设在现实中并非都成立，期权价格往往受到众多其他因素的影响，例如投资者情绪、市场政策以及股息等。因此，许多学者对传统期权定价模型进行了改进。其中，Merton[2-3]对该定价模型做了重要的推广，他在资产价格变化过程中加入了Poisson 跳跃扩散成分，从而提出了跳跃扩散模型。但不管是B-S模型还是跳跃扩散模型都无法刻画出期权价格的“尖峰厚尾”现象。后来，学者们又相继提出了包括二叉树法、蒙特卡洛模拟法、有限差分法、区间定价法以及ε-套利定价法等参数模型。但传统参数模型中的假设均或多或少偏离了真实市场，因此所计算出的期权价格往往与真实市场中的价格有一定偏差。

为了使计算出的期权价格更贴近实际情况，近年来的研究中，非参数模型受到学者们的关注。其中，神经网络由于其强大的拟合与预测能力而被广泛应用。最早将神经网络算法用于期权定价研究的是Hutchinson等[4]，他们以一个两年期的实值期权为样本，利用神经网络从中得出一个与B-S模型充分逼近的定价模型，并对S&P500指数期货期权进行了实证研究，结果优于B-S模型。Qi等[5]将B-S模型的变量作为神经网络的输入，将期权价格作为输出，以S&P500 指数看涨期权作为训练样本，实证表明，神经网络期权定价能力比传统的B-S模型更好；同时提出，只要有足够长时间标的资产的收盘价格，神经网络可以有效地反映出其波动率。Lajbcygier等[6]将不同结构的神经网络与各种参数化模型进行对比，实证结果表明，神经网络的期权定价方法优于各种参数化模型。张鸿彦等[7]建立了混合神经网络和遗传算法相结合的期权价格预测模型，在对香港金融衍生品市场的实证中表明该模型的预测结果要优于传统的B-S模型。

传统的研究中多采用BP神经网络，BP神经网络原理较简单，理论上可以逼近任意的连续函数，但BP神经网络算法也存在收敛速度慢并且容易陷入局部极小值点等缺点。单纯使用BP神经网络其预测精度必然会受到干扰，因此，本文采用改进的粒子群算法（MPSO）对传统的BP 神经网络进行参数与结构优化，再用于期权价格的预测。

本文的主要工作分为3个阶段：第1阶段，对粒子群算法（PSO）进行改进，利用改进后的算法对BP神经网络模型进行参数与结构优化；第2阶段，考虑到权证对应的股票价格的历史波动率是对市场信息的一种反馈，利用广义自回归条件方差模型[8]（GARCH 模型）对股票价格的历史波动率进行预测，并将基于GARCH 模型所获取的波动率作为改进的BP神经网络的输入变量；第3阶段，进一步考虑投资者情绪对期权价格的影响，通过构造剔除基本因素的投资者情绪复合指数，并将其作为改进神经网络的输入变量。最后，随机选取国内10支权证的收盘价格进行实证研究。结果表明，考虑了投资者情绪后的MPSO-BP 神经网络模型学习速度更快、预测精度更高，更加接近市场上真实的期权价格。

2 B-S期权定价模型

传统理论认为期权的标的资产价格Pt遵循几何布朗运动，并且期权的价格是时间与股票价格的函数，即Gt=G（Pt，t）。根据伊藤引理与无套利假设，Black等[1]在求解B-S 微分方程的基础上得到如下B-S欧式期权定价模型：

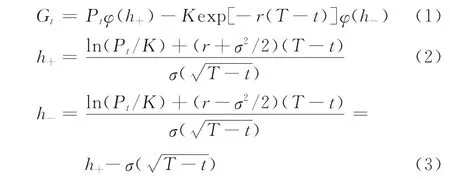
式中：Gt为看涨期权的价格；Pt为标的资产的价格；K为交割价格；ϕ（x）为标准正态分布函数在x处的取值；T-t为距离到期日的时间间隔；r为无风险利率；σ为标的资产价格的波动率。

B-S模型中波动率服从正态分布，但在实际市场中，标的资产价格存在“波动率微笑”现象，并非服从正态分布。因此，B-S模型具有系统性的定价偏差。考虑到大多数股票价格波动率均具有“尖峰厚尾”现象[9]，故本文运用GARCH 模型对权证股票的历史波动率进行测算。

3 MPSO-BP神经网络模型

3.1 BP神经网络

BP神经网络属于多层前向性神经网络的一种，在该网络中，信号前向传递，而误差反向传递。信号在逐层传递的过程中根据预测误差不断调整网络的权值与阈值，从而逐渐逼近期望输出。因此，它具有很强的非线性映射能力。BP 神经网络结构如图1所示。

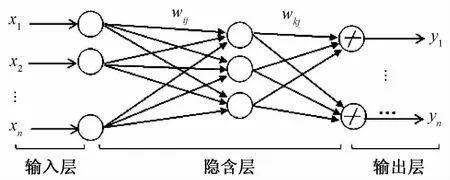
图1 BP神经网络结构

BP神经网络通常由输入层、隐含层和输出层3部分组成。设输入层共有N个输入向量元素，每个输入均被赋予一定的权值w ij。输入向量X=｛x1，x2，…，x n｝，其中X i为第i个输入向量，X i=｛x i1，x i2，…，x ip｝T，i=1，2，…，n。隐层有S个神经元组成，隐层第j个神经元的输出为

式中：f（·）为隐层激活函数；w ij为输入层第i个向量与隐层第j个神经元间的连接权值；aj为第j个神经元的阈值，即

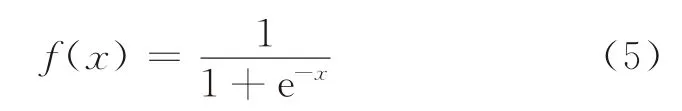
输出层的输出个数为M，期望输出向量Y=｛y1，y2，…，y m｝，则输出层神经元的输入输出关系为

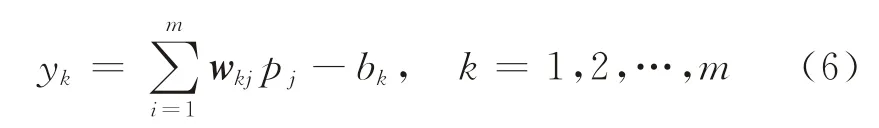
式中：y k为输出层第k个神经元的输出值；w kj为输出层第k个神经元与隐层第j个神经元间的向量权值。

BP神经网络在进行训练的过程中，根据网络的预测输出Ok与期望输出Y k之间的误差e k不断地进行权值和阈值更新，直至误差满足设定要求或达到最大迭代次数，算法迭代才结束。

网络预测误差为

权值w ij、w kj和阈值a j、bk的更新函数分别为：

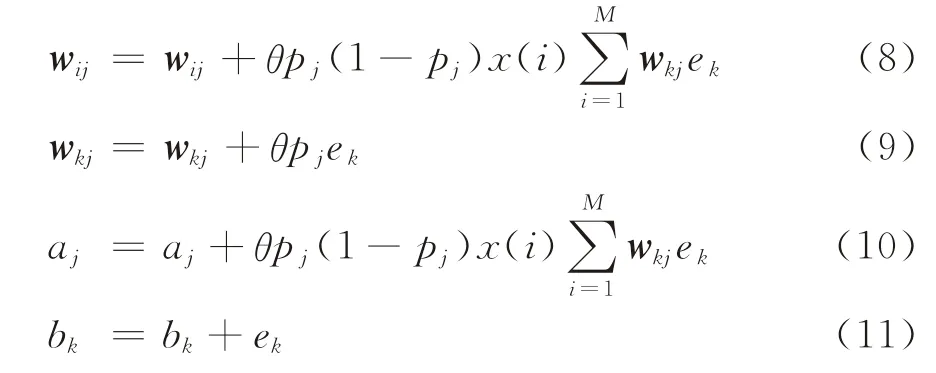
式（8）～（10）中，θ为学习速率。

3.2 PSO 算法及改进

粒子群算法最早由Kennedy等[10]提出，该算法来源于对鸟群觅食过程中迁徙和聚集行为的模拟，是一种群体智能的优化方法。在每个优化问题中，每个候选均解释为搜索空间中的一个粒子，每个粒子均有一个由目标函数决定的适应度值，粒子向搜索空间中飞行的过程即搜寻最优解的过程，粒子飞行的方向与距离由其速度决定。在飞行过程中，粒子均会根据飞行经验不断调整飞行状态，直至寻找到最优解。

设在一个N维的目标搜索空间中，PSO 算法中由M个粒子组成一个群落，每个粒子在空间中的位置均用一个N维向量表示，记第i个粒子是位置向量X i=｛x1，x2，…，x n｝，该向量X i为一个潜在解。每个粒子具有自身的速度参数，分别记为V i=｛v1，v2，…，vn｝。粒子在飞行过程中，速度和位置状态随着每次迭代不断更新。每次迭代中，每个粒子都会记录下已获取的最优解，即个体极值Si=｛si1，si2，…，sin｝，整个 粒子群记录下的最优全局极值，记为Sg=｛sg1，sg2，…，sgn｝。在第k+1次迭代时，粒子根据个体极值与全局极值更新其速度与位置的规则为：

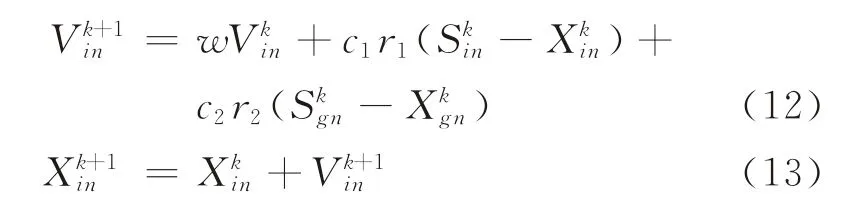
式中：w为惯性权重，是用于控制速度的权重一般取值为（0.1，0.9）；k为当前迭代次数；c1为粒子自身向全局最优位置调节的前进步长，c2为粒子向种群最优位置调节的步长，c1、c2统称为加速系数；r1、r2为（0，1）上的随机数。

虽然粒子群算法具有易实现、收敛快以及搜索能力强的特点，但粒子群算法容易陷入局部最优值从而降低寻优精度。为了克服上述缺点，本文借鉴遗传算法中的变异思想，将单点变异算子引入PSO算法中[11]。在算法进行寻优的过程中，使某些粒子具有自适应变异功能，从而使陷入局部最优极值的粒子跳出当前位置，拓展了粒子群的搜索空间，提高了PSO 算法的寻优能力。

单点变异算子原理如图2所示，首先对父代基因序列随机产生变异点，再根据变异点位置改变对应位置的基因值。在传统的遗传算法中，变异算子均采用非均匀变异算子。将单点变异算子引入粒子群算法中，单点变异算子随机选取粒子进行变异，选中的粒子在每次更新后能够以特定的概率初始化，从而跳出局部最优值位置。

图2 单点变异算子操作示意图

对粒子群算法进行自适应变异优化后，进化过程中最优个体适应度值变化如图3所示。通过对比可知，将单点变异算子引入粒子群算法后，粒子能够较快地跳出局部极小值，收敛速度与寻优精度均有所提高。

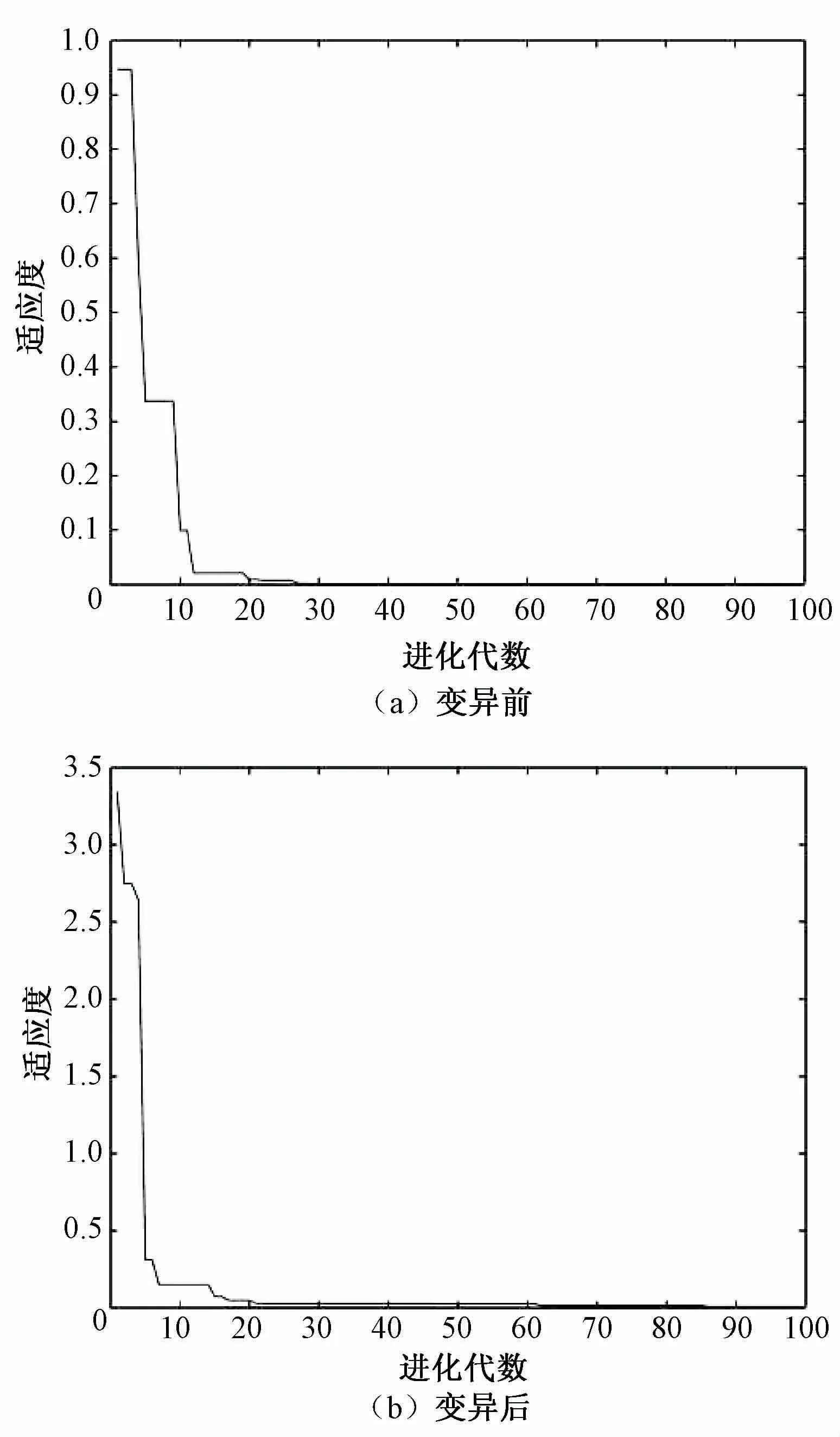
图3 最优个体适应度值对比

3.3 基本输入变量

根据B-S期权定价模型，影响期权价格的变量分别为：资产标的价格、期权执行价格K、距离到期时间的间隔、无风险利率r和资产波动率σ。其中，前4个变量均已知。B-S模型中波动率σ为常数，但标的资产价格的波动率实际上是不断变化的，为了对波动率进行更精准的估计，考虑采用GARCH 模型对波动率进行估计：

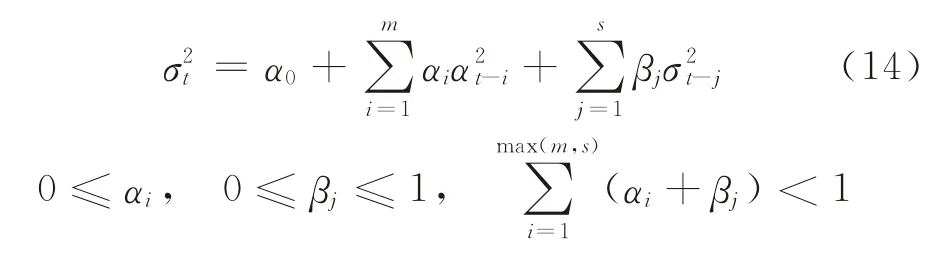
式中：αt=μt-为关于方差在t时刻的新息；σt为t时刻的波动率；αi和βi均为参数，可用最大似然法估计。因此，可以根据历史值准确计算出特定时刻的波动率大小。

GARCH 模型可以很好地解释产生在金融时间序列中的“波动率聚集”现象。此外，GARCH 过程分布的尾部比正态分布厚，满足资产价格分布的“尖峰厚尾”现象。因此，基于GARCH 模型估计获得的资产价格波动率更加贴近实际情况。

3.4 考虑投资者情绪的影响

传统理论通过构建数学模型对期权价格进行估计，但实证表明，期权价格除了受到上述5个基本变量的影响，还会受到投资者情绪的干扰[12]。如果投资者普遍认为市场行情较好，过热的投资者情绪很容易推动期权价格与成交量的上涨；相反，如果市场行情不佳，低落的投资者情绪很容易减少成交数量并拉低期权价格。随着研究的推进，越来越多的学者认为投资者情绪的影响对衍生品定价，尤其是对期权的价格不可忽略[13-14]。

为了准确度量投资者情绪对期权价格的影响，本文采用Baker等[15-16]所提出的基于主成分分析法构建的投资者情绪复合指标，并进一步剔除基本因素的影响。首先借鉴国内外已有的研究成果，筛选出最具有代表性的投资者情绪度量指标；其次，为了进一步剔除基本因素对投资者情绪的影响，将原始情绪指标对主要的宏观经济变量进行回归，并将回归得到的残差作为主要变量进行主成分分析；最后，对通过主成分分析提取出主成分对主要宏观经济变量进行检验，从而验证投资者复合指标的纯度与代表性。并将“提纯”后的投资者情绪复合指标作为改进神经网络的输入变量之一融入到模型中。

因此，考虑投资者情绪之后的改进神经网络期权定价模型在原有5个变量的基础上，再添加剔除了基本因素影响后的投资者情绪复合指标作为模型的输入。

3.5 基于改进的PSO-RBF的期权定价模型

BP神经网络算法的参数是决定其准确性的关键。如图4所示，将改进后的粒子群算法用于训练BP神经网络的方差、权值与中心值，可以优化神经网络的参数与网络结构，同时进一步提高神经网络的准确性与收敛速度。具体训练步骤：

（1）样本预处理。将样本数据归一化，使所有数据处于（0，1）范围内，即

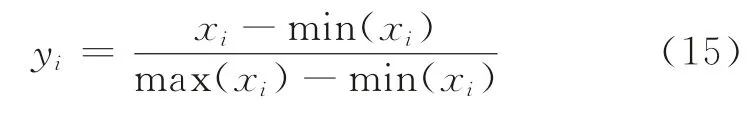
图4 基于改进的PSO 算法优化BP神经网络参数流程图

式中：｛x i｝为输入原始数据；｛y i｝为归一化后的输出数据；max（x i）、min（x i）分别为原始数据的最大值和最小值。

（2）参数初始化。生成种群粒子并将参数w ij、w kj赋予随机值用以初始化粒子位置、速度以及种群规模。

（3）计算评价函数。对改进的神经网络模型输入训练样本，得到输入输出响应后，选用平均误差的绝对值作为改进神经网络模型的评价函数。根据适应度公式计算适应度值，最后确定个体与种群的最优值。适应度公式定义为

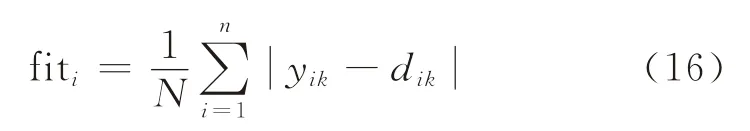
式中：yik为训练输出值；d ik为期望值；N为训练样本个数；M为输出神经元个数。

（4）每一次迭代根据式（6）、（7）更新位置与速度信息。在单点变异算子作用下，每次更新均以一定概率初始化粒子群；如果根据式（8）、（9）得出的值更优，则重新设定个体极值与种群极值的新值。

（5）判断是否达到最大迭代次数或是否满足优化目标。满足条件终止算法；否则，返回（3）。

4 实证分析与比较

4.1 样本数据的获取与预处理

为了验证改进神经网络模型的有效性，本节以大智慧与万德数据库中的国内已摘牌权证的历史价格为研究对象。选择鞍钢JTCI认购权证价格的历史数据作为实证分析例子，并从国内55支已摘牌权证中随机选取其余9支认购权证的历史价格进行实证分析。

样本数据为看涨期权的日数据，因此，时间间隔T-t=1。选取当时的3个月银行sing存款利率为无风险利率r。敲定价格K可以从权证上市公告书获取。由于鞍钢JTCI认购权证所对应的股票为鞍钢股份，鞍钢JTCI发行时间为2005-12-05～2006-11-28，故选取2005-11-01～2006-11-28共计262天的股票收盘价格的对数收益率时间序列作为建立估计波动率的GARCH 模型的样本，然后估计模型参数的估计与建模。

为了判断样本对数收益率时间序列是否存在ARCH 效应，首先观察对数收益率分布直方图是否满足正态性。由图5可以发现，对数收益率的分布具有较为明显的尖峰厚尾现象，通过J-B 检验拒绝了其正态性假设。

图5 鞍钢JTCI对数收益率直方图

接下来，进一步检验对数收益率时间序列的平稳性以及相关性。由表1可见，单位根检验中的P值接近0，表明序列平稳。再进行自相关和偏相关检验，结果如图6所示，说明序列存在明显的一阶、二阶自相关。利用拉格朗日乘数检验法对残差进行检验，通过F检验，可见，对数收益率时间序列的确存在较为明显的ARCH 效应，可以建立GARCH 模型。

表1 鞍钢JTCI对数收益率单位根检验

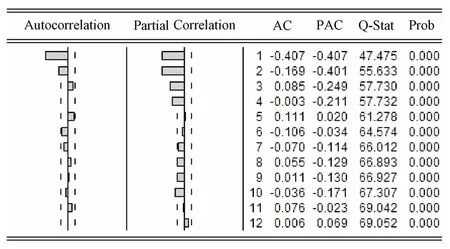
图6 鞍钢JTCI对数收益率自相关、偏相关分析图

利用EViews8.0估计GARCH 模型的参数，并在5%的显著水平下进行有效性检验。检验结果如表2所示。

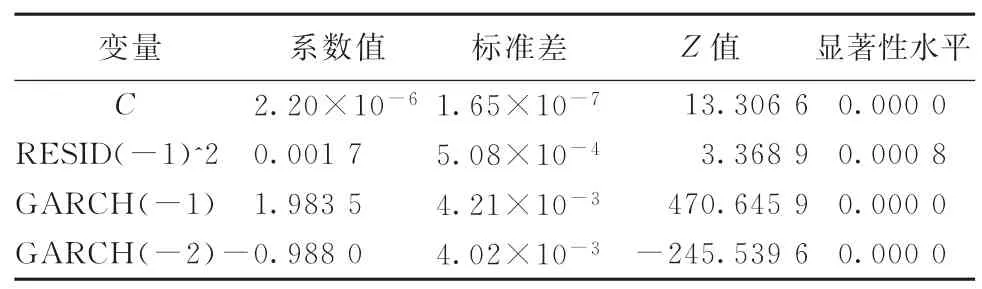
表2 鞍钢JTCI对数收益率GARCH 参数估计结果

鞍钢JTCI对数收益率序列满足GARCH（1，2）模型，并且所有参数P值均通过检验。因此，建立的GARCH（1，2）模型为

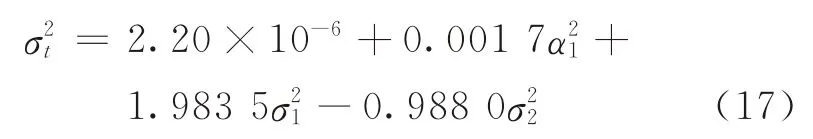
为了进一步验证模型的有效性，采用ARCHLM 检验法对已经建立的GARCH（1，2）模型的残差在滞后4阶下进行ARCH 效应检验，检验结果如表3所示。根据F统计量与P值结果，不能拒绝模型中不存在ARCH 效应的原假设，因此所建立的模型中残差已经不存在ARCH 效应，该模型有效。

表3 GARCH(1，2)模型的ARCH-LM 检验结果

利用Eviews8.0 获取所建立模型的拟合对比图，如图7所示，通过对实际数据与残差效果的对比，模型的残差大部分落在5%以内。可见，该模型的拟合效果较为理想。

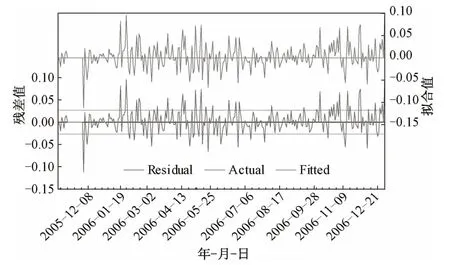
图7 基于鞍钢JTCI的GARCH（1，2）模型拟合对比图

根据上述步骤，分别对其余9支认购权证所对应的股票价格对数收益率时间序列建立GARCH模型，并对所建立的模型的残差分别进行ARCHLM 检验。若模型中的残差还保留ARCH 效应，则需要进一步修正模型，分别对GARCH 模型的阶数作进一步调整，直至ARCH-LM 检验结果的P＜5% 的临界值，说明残差中的ARCH 效应已经被剔除干净。最后，获得所有模型的参数估计结果如表4所示。

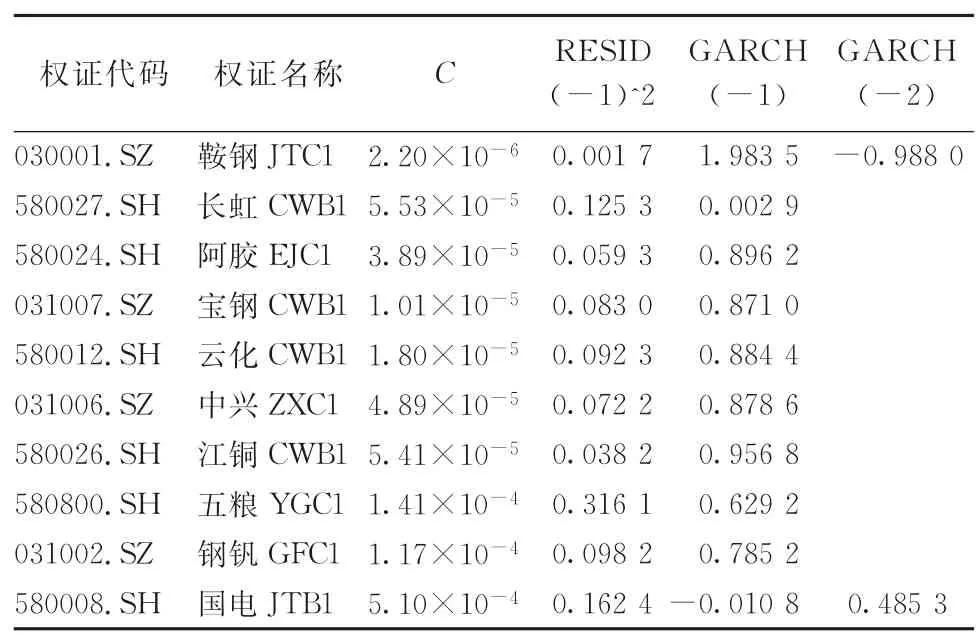
表4 GARCH 模型参数估计

选取的10支认购权证中有4支备兑权证，6支股本权证。由于备兑权证由第三方机构发行，不需要增发股票，而股本权证由上市公司发行，并会因为增加总股本而导致价格稀释，故在对股本权证进行定价时需要考虑“稀释效应”[17]。此外，还要充分考虑每只权证因除息而对行权价格与行权比例的调整。选取的每支权证的上市日期以及存续时间有一定差异，因此，可以减少特定时间段内的不确定因素对定价造成的偏差。

4.2 神经网络结构与参数的确定

利用改进粒子群算法优化BP 神经网络的流程如图4所示，本文采用3层BP神经网络结构，隐层与输出层的激活函数选用tansig传递函数，同时采用Levenberg-Marquardt算法作为BP 神经网络的训练函数。BP 神经网络的学习步长设定为0.01，最大训练次数设定为500，最大容许误差设为0.001。

BP神经网络的结构中对模型精度影响最大的是隐层节点数的确定，它由输入输出的参数个数共同决定。传统的B-S期权定价模型共有5个输入变量，分别为：资产标的价格Pt、期权执行价格K、距离到期时间、无风险利率和资产波动率，输出变量为期权价格Gt。采用下式用于确定最佳隐含层节点数[18]：

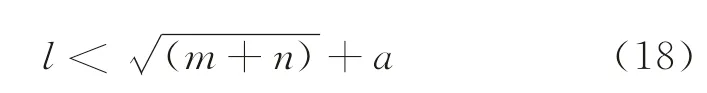
式中：l为隐含层节点数；m、n分别为输入、输出变量个数；a为（0，10）间的常数。

由于不同的输入变量与输入数据均会影响最佳节点数的选择，基于传统模型的5个输入变量，首先根据式（18）确定最佳节点数的大概范围，然后采用试凑法在不同的隐层节点数下各迭代200次筛选出预测整体预测误差相对较小的节点数。预测误差与隐层节点数的关系如图8所示。由图8可见，BP神经网络的预测误差随隐层节点数的增加整体呈现先减后增的趋势，故可得最佳的隐层节点数为9。因此。改进神经网络的最优结构为5-9-1。

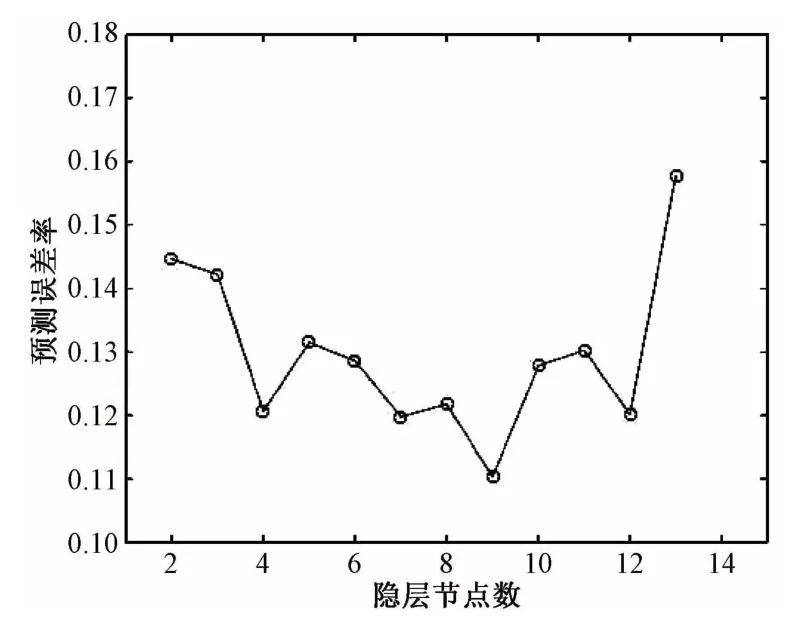
图8 隐层节点数与预测误差率关系示意图

为了进一步提高神经网络的预测精度，采用改进的粒子群算法用于优化BP神经网络的权值与阈值。粒子群算法中的每个粒子代表神经网络的权值与阈值，通过粒子寻优获取权值与阈值的最优解。每个粒子维数为2，种群规模设定为50，进化次数为500，加速度系数设置c1=c2=1.494 45；同时，为了避免粒子盲目搜索，位置与速度的限制区间设定为（-5，5）和（-1，1）。

根据初始设定的参数可以得到BP 神经网络的初始权值与阈值，由于改进神经网络的最优结构为5-9-1，故输入层与隐层间共有45个权值，隐层节点的阈值有9个，隐层与输出层间共有9个权值，输出层节点的阈值则有9个。再根据训练数据获得权证的预测价格，之后将权证预测价格与权证的实际价格的误差绝对值作为个体适应度值，种群粒子的适应度越小，则说明个体越优。最后，将改进粒子群算法得到的最优个体值赋予BP神经网络的权值与阈值，即可得到基于改进粒子群算法优化下的BP 神经网络模型。

4.3 投资者情绪复合指数的构造

构造能有效反应投资者情绪的复合指标的首要问题就是代理变量的选取。选取具有代表性的相关变量作为主成分分析指标时，需要同时考虑指标的有效性以及可获取性。结合已有研究成果以及目前我国国内衍生品交易市场的实际情况[19-21]，本文选取的指标包括：A 股换手率Turn、投资者新增开户数O、消费者信心指数C、好淡指数H以及股票市场成交量Vol。考虑到本文中用于实证的权证价格历史数据的时间跨度为2005-12～2011-08，因此，选取相相应时间段的投资者情绪变量的月度数据共计69个观测值，所有数据先经过标准化后再进行主成分分析。

根据Baker等投资者情绪复合指数[15-16]构建的方法，首先需要提前确定各个变量的提前滞后关系。选取所有5个指标的当期值以及滞后值共10个指标，利用主成分分析法构建一个综合指数Comp，经过检验，KMO 值为0.672，Bartlett球度检验的P值为0.000，P＜5%的显著水平说明可以进行主成分分析。

再分别计算综合指数Comp与各个变量当期值与滞后期值的相关系数，相关系数越高，说明变量中含有的投资者情绪因素越多。相关性分析结果如表5所示，根据各个变量当期数据和滞后一期值分别与综合指数Comp的相关系数对比结果。因此，分别选择换手率和好淡指数的当期值，投资者新增开户数、消费者信心指数以及股票市场成交量的滞后一期值作为构建投资者情绪复合指数的指标。

表5 综合指数与各个变量间的相关系数表

由于用于构建投资者情绪的主要指标中除了反应投资者情绪的因素外，也包含了宏观经济等基本因素。为了获得更“纯”的投资者情绪复合指数，采用Baker等[15-16]的方法进一步剔除基本因素的影响。首先，选取消费价格指数CPI、宏观经济景气指数MCI以及国内生产总值GDP等3个变量作为宏观经济变量的主要指标[20-21]，但是由于国内生产总值为季度数据，考虑到其数据特性，故采用工业增加值的同比增长率IAV 作为替代[20]，所有数据来源于万德数据库，均为月度数据，其时间跨度与权证历史价格数据保持一致。将上述5个变量分别与3个宏观经济变量进行回归，并通过检验结果不断调整回归的变量个数直到方程和系数显著性通过检验。最后，采用相应的残差作为主成分分析的变量。

主成分分析结果如表6 所示。经检验，KMO值为0.612，Bartlett球度检验的P值为0.000，因此，可以进行主成分分析。通过主成分分析法共提取出两个主成分，特征根均大于1，并且累计解释率达到86.071%。公因子方差分析结果表明，原始变量中的提取信息率均在80.8%以上，因此，主成分分析的效果较好。

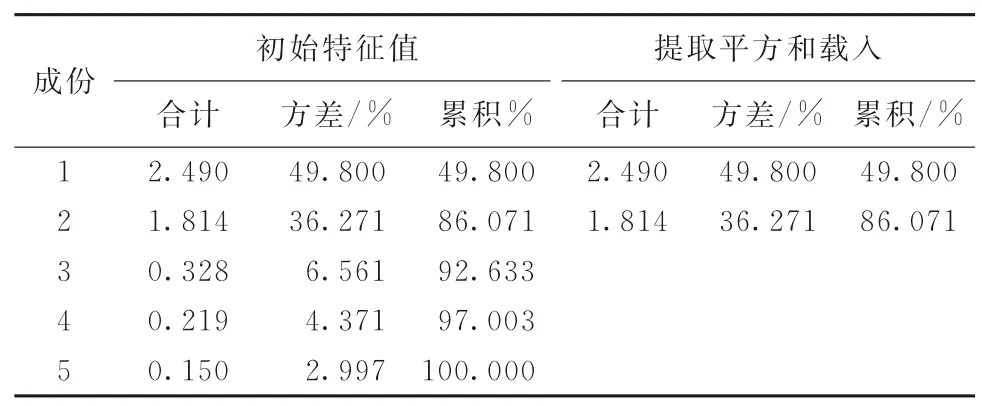
表6 主成份分析结果

最后，通过初试因子载荷矩阵中的所有系数除以主成分特征值的平方根得出主成分系数向量，再与标准化后的变量残差数据相乘得出每个主成分表达式，并根据每个主成分的贡献率大小进行加权求和，便可得到最后的投资者情绪复合指数Sentiment。

为了验证所获得的投资者情绪复合指数是否较纯，将复合指数分别与3个标准化后的宏观经济变量进行相关性分析，结果如表7所示。由相关性分析结果可见，复合指数与主要3个宏观经济变量的相关系数均小于0.1，P＞10%，说明指数Sentiment与其他3个宏观经济变量不存在相关性。由于本文并未将无风险利率作为主要宏观经济变量加以分析，为了进一步验证结果的真实性，采用标准化后的3个月定期银行存款利率作为无风险利率指标，与所构造的投资者情绪复合指数进行相关性分析，相关系数绝对值小于0.1，同样不能拒绝两者不存在相关性的原假设，说明此时复合指数已经将基本因素剔除干净。

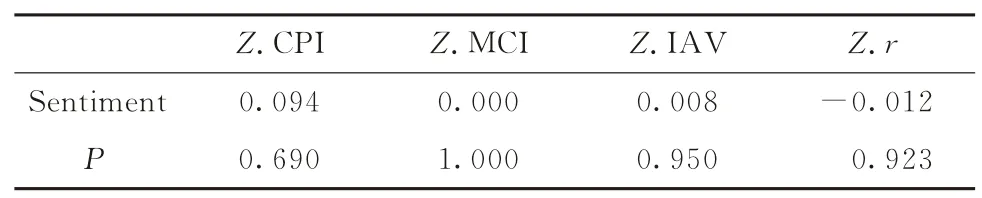
表7 投资者情绪复合指数与宏观经济变量相关性分析

4.4 实证结果

实证中采用的10支认购权证共计4 087个数据，其中每只权证抽取50个数据作为测试集，测试样本共计500个数据，其余3 587个数据作为神经网络的训练样本。将训练样本预处理后，按照图4所示的训练步骤对样本进行训练，并利用改进的粒子群算法确定BP 神经网络的权重以及网络结构，同时研究B-S模型、BP 神经网络、PSO-BP 神经网络以及MPSO-BP神经网络4种方法的期权价格预测精度。本文采用平均相对预测误差作为模型的评价标准，即

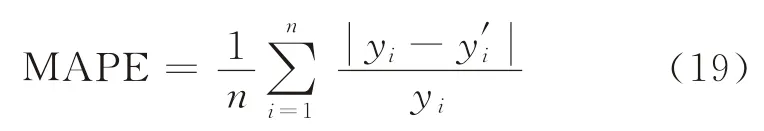
首先针对改进的PSO-BP神经网络模型的有效性进行实证，同时选择B-S模型、BP神经以及PSOBP神经网络进行对比研究，迭代次数为500。该部分不考虑投资者情绪的影响，因此，输入变量为5个，实证结果如表8所示。

表8 各模型预测结果MPD比较

由表8可见，传统B-S模型对期权价格的预测精度较差，相比于参数化模型，3种BP 神经网络对期权价格的预测能力有所加强，说明了BP 神经网络模型用于期权定价的可行性。其中改进的PSOBP神经网络混合模型对期权价格预测精度有了很大的提高，说明了本文所提出的MPSO-BP 神经网络模型优于传统的BP 神经网络以及PSO-BP 神经网络。并且，根据GARCH 模型预测标的资产价格的历史波动率更符合实际情况，提高了权证的定价精度。

最后，为了验证投资者情绪对期权价格的影响，选取BP、PSO-BP及MPSO-BP 神经网络模型进行实证对比，由于B-S模型不考虑投资者情绪对期权价格的影响，故只选取3种神经网络模型，迭代次数为500，其余参数设置不变。本文对BP 神经网络、PSO-BP神经网络及MPSO-BP 神经网络模型的输入作出改变，在原来的5个输入变量基础上增加反应投资者情绪的复合指数Sentiment。此时，由于输入变量变为6个，需要重新按4.2节步骤确定改进神经网络模型的结构与相关参数，同样利用式（18）与试凑法确定隐层节点数的大致范围。最后，基于不同的隐层节点数各自迭代200次计算误差率，从而确定出改进神经网络的最优结构为6-11-1。

实证结果如表9所示。融入了投资者情绪影响后，3种神经网络模型对10支权证中超过7支权证的价格预测精度均进一步提高，其中考虑投资者情绪影响后的MPSO-BP神经网络模型对期权价格的预测误差总体最低。这说明，融入了投资者情绪的影响后，期权的价格更贴近实际的价格。实证结果表明，在中国权证交易市场上，投资者对期权价格的影响是不可忽略的一个因素。

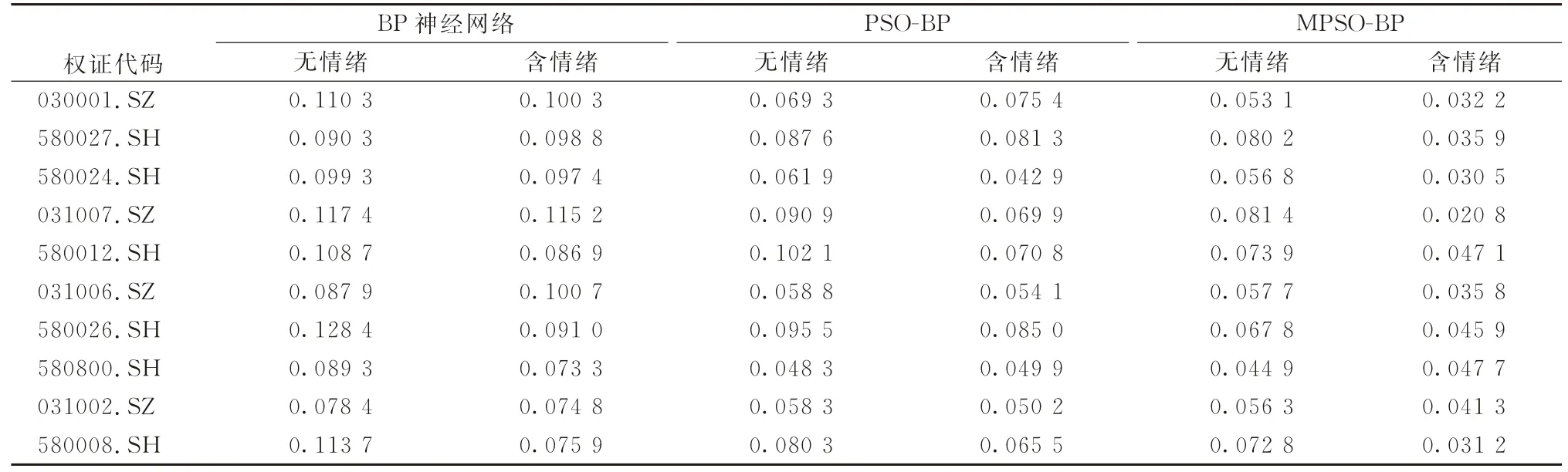
表9 考虑投资者情绪后的预测结果MAPE比较

5 结语

本文首先针对传统的PSO 算法易陷入局部极值以及寻优精度不稳定的问题，将遗传算法中的单点变异算子引入传统PSO 算法中，赋予粒子自适应变异的能力，从而扩大粒子群的寻优范围。将改进的PSO算法与BP神经网络相结合，利用MPSO 算法对BP神经网络的参数与模型结构进行优化。由于波动率是影响期权价格的重要因素，本文提出，利用GARCH 模型估计出每支权证对应的股票的收盘价格的历史波动率，并将获得的波动率作为MPSO-BP神经网络的输入。最后，考虑到市场上投资者情绪可能对期权价格有影响，采用Baker等[15-16]的基于主成分分析法构造投资者情绪复合指数，并将构造剔除了基本因素后较纯的投资者情绪复合指数引入到改进的改进神经网络模型中。

通过实证结果表明，传统的B-S模型假设过于严苛，所以期权定价的误差较大。相比于传统的BS模型及BP神经网络模型，本文提出的MPSO-BP神经网络模型有效提高了期权价格预测的精确度及算法的收敛速度，证明了模型的有效性。进一步考虑了投资者情绪的影响后，3种神经网络均进一步缩小了期权定价的误差，其中MPSO-BP 神经网络模型的预测误差仍为最低。这也反映出目前在我国国内权证市场进行期权定价研究时，投资者情绪是不可忽略的因素。本文的实证结果对我国期权定价研究具有较高的参考价值，该方法可进一步推广至其他国家与地区，进而研究投资者情绪对不同国家中期权定价的影响。