济南市区土体动剪切模量比和阻尼比的统计分析
,,,,
(1.济南轨道交通集团有限公司,济南 250101;2.同济大学 地下建筑与工程系,上海 200092)
1 研究背景
随着地铁的大量兴建,抗震性能研究日益引起重视。地铁结构在地震作用下的响应机理与周围土体的动力特性密切相关,而土体的动力特性一般由土体动力本构模型表征,包括动剪切模量比Gd/Gdmax和阻尼比λ随剪应变γd的变化曲线。它们是研究地震作用下土体及土-结构相互作用体系动力特性的基础,也是利用各种抗震设计方法进行地铁结构动力分析的前提条件[1]。
目前,国内外学者已经对土体的动力本构模型开展了广泛研究。国外学者Hardin和Drnevich[2]给出了最大动剪切模量Gdmax的经验公式,并用双曲线形式的Hardin-Drnevich模型描述动剪切模量比Gd/Gdmax与剪应变γd之间的关系;Martin和Seed[3]基于Hardin-Drnevich模型提出了Davidenkov模型,改进方法是增加了3个土体试验参数。国内学者陈国兴等[4]为克服Davidenkov模型剪应力随剪应变增长而无穷增长的缺点,采用破坏剪应变的上限值作为分界点,提出了分段函数形式的修正Davidenkov模型;齐文浩等[5]建立了指数形式的土动力本构模型,并用土体的共振柱试验对该模型进行了验证。虽然土体的动力本构模型具有通用性,但是模型参数取值往往具有明显的地域特征。《工程场地地震安全性评价工作规范》(DB 001—94)[6]给出了动剪切模量比Gd/Gdmax和阻尼比λ的规范取值,但是因取样地域范围小,试验条件较差,代表性有限;孙锐等[7]研究了国内17个省份42个地区的588组不同类型土样,并给出了常规土类动剪切模量比Gd/Gdmax和阻尼比λ的推荐值,不过许多学者研究发现,不同地区土体动参数的取值与上述推荐值存在差异[8-12]。
针对济南市区的土体动力参数,目前系统的研究还较少。因此,在济南市的地铁建设中,为了对建设场地进行地震安全评价,开展了代表性土层的动三轴试验。本文对试验成果进行了统计分析,并与其他地区的研究成果进行了对比、讨论。一方面可以对济南市区土动力特性的特殊性有较全面的认识;另一方面也可为工程抗震设计提供参考。
2 试验概况
2.1 试验仪器和步骤
采用DDS-70型微机控制电磁式多功能动三轴试验系统,主要技术指标见表1。试验按《土工试验规程》(SL 237—1999)[13]进行,采用Φ39.1 mm×80 mm的标准试样,施加的动荷载为正弦波激振力,振动频率为 1 Hz,获得5×10-6,1×10-5,5×10-5,1×10-4,5×10-4,1×10-3,5×10-3,1×10-2共8个典型剪应变下的动剪切模量比和阻尼比。

表1 DDS-70型动三轴试验系统主要技术指标Table 1 Main technical indexes of DDS-70 dynamic triaxial test system
试验过程中,将预先真空饱和的试样置于三轴室内,在等固结比应力下固结,围压大小根据试样所处深度对应的有效应力确定。待试样固结完成后,在不排水条件下对其施加由小到大的轴向激振力,以进行动三轴试验。
2.2 试验原理
根据土体的σd-εd关系曲线(图1(a)),由式(1)确定动弹性模量Ed;根据土体轴向变形与剪切变形的关系,分别由式(2)和式(3)确定动剪切模量Gd和动剪应变γd;根据土体在动力作用下的滞回效应(图1(b)),由式(4)确定等效滞回阻尼比λ。
(1)
(2)
γd=(1+ν)εd;
(3)
(4)
式中:σd为动应力,其中土体所能承受的最大动应力为σdmax;εd为动应变;γd为动剪应变;Ed为动弹性模量,其中Edmax为γd趋近于0时的最大动弹性模量;Gd为动剪切模量,其中Gdmax为最大动剪切模量;ν为泊松比,取值为0.5[14];A为图1(b)中滞回圈ABCDA的面积,其中滞回曲线的循环次数为10次;As为三角形OAE的面积。

图1 试样的应力-应变关系曲线和应力-应变滞回圈Fig.1 Stress-strain curve of soil specimens and hysteresis loop of stress-strain relation
2.3 试验土样
济南市区位于泰山山脉以北、黄河冲积平原以南,区域内地形地貌空间变化显著。地形自东南至西北由高渐低,地貌按成因类型依次划分为:剥蚀-溶蚀丘陵区、残丘区、山间平原区、山前倾斜平原区和冲积平原区[15]。考虑仪器性能及钻探影响,本文选取区域内广泛分布的黏土、粉质黏土和黄土进行试验,其中粉质黏土根据地质年代划分为Q4,Q3,Q23层。本研究共取样128组,试样取自济南地铁R1线、R2线和R3线拟建场地,取样深度介于2.3~46.8 m,各试样的描述、取土深度、重度及取样数量见表2。
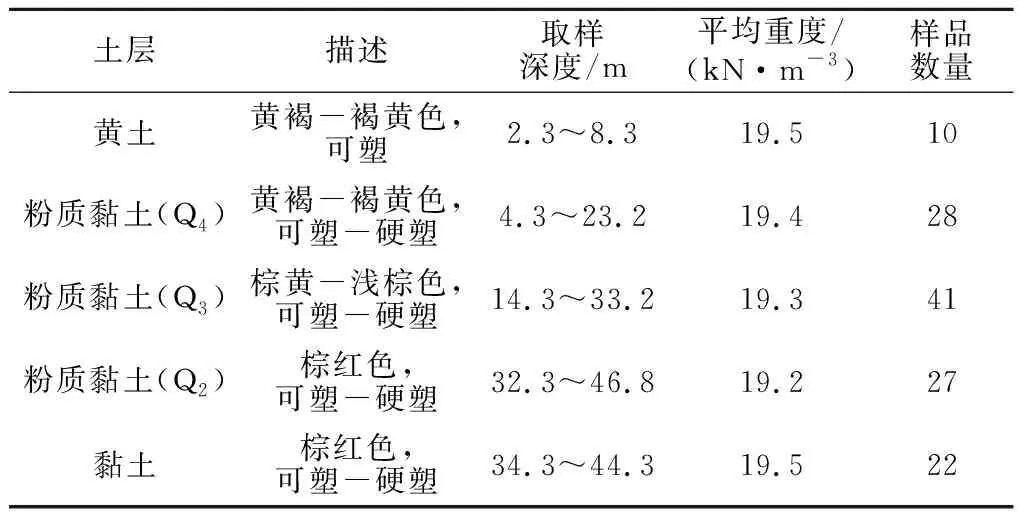
表2 土样基本情况Table 2 Basic situation of soil specimens
3 试验结果与拟合分析
3.1 试验结果
图2是动三轴试验得到的黄土的动剪切模量比Gd/Gdmax和阻尼比λ随剪应变γd的变化。从图2中可以看出,随着动剪应变的增大,动剪切模量比减小,阻尼比增大,这说明在动力作用下土体表现出非线性特性。不过,试验数据的离散性较大,这可能由于土体本身动力性质的差异,如埋藏条件、有效应力、塑性指数和相对密度等因素引起,也可能由于试验条件和操作,如试样成型的质量和方法、固结压力、固结时间、排水状态以及操作方式等因素引起[16]。其他土层也存在类似规律,这里不再赘述。

图2 济南市区黄土动剪切模量比和阻尼比随动剪应变的变化Fig.2 Changes of dynamic shear modulus ratio and damping ratio of loess against dynamic shear strain
3.2 拟合分析
对试验结果进行拟合时,常用的土体动力本构模型有Hardin-Drnevich模型[2]和Davidenkov模型[3],不过2种模型各有优缺点[17]。本文吸取2种动力本构模型的优点,分别用式(5)和式(6)对动剪切模量比Gd/Gdmax和阻尼比λ进行拟合。
(5)
(6)
式中:γr为参考剪应变;λmax为土体最大阻尼比;β为土体试验参数。

表4 不同土层在典型剪应变下动剪切模量比Gd/Gdmax和阻尼比λ的取值Table 4 Values of dynamic shear modulus ratio Gd/Gdmax and damping ratio λ of different soil layers at typical shear strain
不同土层的拟合参数和拟合系数见表3。从表3中可以看出,式(5)对动剪切模量比Gd/Gdmax的拟合效果较好,不同土层的相关系数均达到0.94以上。黄土、粉质黏土(Q4,Q3,Q2)和黏土的参考剪应变γr依次增大。出现上述变化规律的原因是土体的结构性:黄土的取土深度较浅,土体结构疏松、多孔;粉质黏土随着沉积年代的增加埋深增大,结构性增强;黏土埋置最深,土体结构密实程度最强。应力波在土颗粒中的传播要快于在土孔隙中的传播,土的结构性越强,则土颗粒接触越多,因此黏土中的应力波传播较快,使得相同剪应变下其动剪切模量比Gd/Gdmax较大,进而导致其参考剪应变γr取值较大。式(6)对阻尼比λ的拟合系数稍低于式(5)对动剪切模量比Gd/Gdmax的拟合系数,值在0.9左右。对于不同土层的最大阻尼比λmax,黄土最大,黏土最小,粉质黏土介于两者之间,不过不同沉积年代的粉质黏土相差不大;对于土体试验参数β,不同土层的取值均在0.4左右。
表3不同土层的拟合参数及拟合系数R2
Table3FittingparametersandcoefficientR2ofdifferentsoillayers

土层Gd/Gdmax的拟合参数λ的拟合参数γrR2λmaxβR2黄土0.001 5070.957 70.218 60.407 50.917 4粉质黏土(Q4)0.001 6110.947 00.201 30.450 60.922 3粉质黏土(Q3)0.002 0930.958 30.206 60.382 50.906 8粉质黏土(Q2)0.002 1230.941 10.203 30.447 20.902 6黏土0.002 4630.951 10.189 20.389 80.845 6
4 成果及对比分析
4.1 典型剪应变下的取值
动剪切模量比Gd/Gdmax和阻尼比λ是随剪应变γd变化的连续函数,不过目前工程上使用的是数字化结果,即给出在5×10-6,1×10-5,5×10-5,1×10-4,5×10-4,1×10-3,5×10-3,1×10-2这8个典型剪应变下动剪切模量比Gd/Gdmax和阻尼比λ的取值。根据本文提出的拟合公式,可计算出济南市区不同土层在8个典型剪应变下的取值,见表4。地震作用时土体的剪应变一般在1×10-5~5×10-3之间[18],因此从表4中看出在地震作用下不同土层动剪切模量比Gd/Gdmax和阻尼比λ的取值相差不大,这说明济南沉积土体在动力作用下的一致性较好。
4.2 结果的对比分析
为了验证研究结果的可靠性,将本文得到的结果与其他地区的成果进行对比分析。在研究背景部分中已经指出,许多学者对不同土类的动剪切模量比Gd/Gdmax和阻尼比λ的进行过研究,其中,比较有代表性的是孙锐等[7]给出的全国范围内动剪切模量比Gd/Gdmax和阻尼比λ的极大值、极小值和均值等推荐值。不过需要指出的是,孙锐给出的推荐值中不包括黄土,并且粉质黏土未区分地质年代。因此,将本文得到的不同沉积年代的粉质黏土数据按照取样数量进行加权平均后与孙锐给出的推荐值进行比较,而黏土数据直接进行比较。

图3 动剪切模量比的比较Fig.3 Comparison of dynamic shear modulus ratio
图3是动剪切模量比的比较。从图3中可知,本文得到的粉质黏土和黏土的动剪切模量比Gd/Gdmax均在孙锐给出的统计值包络线之内,不过明显大于孙锐给出的均值而更接近于极大值。相同剪应变下,粉质黏土的动剪切模量比稍小于孙锐给出的极大值,而黏土的动剪切模量比几乎与孙锐给出的极大值重合。
图4是阻尼比的比较。从图4中可以看出,本文得到的粉质黏土和黏土的阻尼比λ亦在孙锐给出的统计值包络线之内,接近于孙锐给出的均值。相同剪应变下,粉质黏土的阻尼比与孙锐给出的均值相差很小。黏土的阻尼比要小于孙锐给出的均值,以剪应变5×10-5为界,当剪应变小于该值时,两者的阻尼比相差不大;当剪应变大于该值时,两者的阻尼比相差较大,本文结果在孙锐给出的均值和极小值之间。

图4 阻尼比的比较Fig.4 Comparison of damping ratio
通过以上分析可知,总体上看,济南市区土体的动剪切模量比较大,阻尼比较小,说明土体的动力性质较好,对抗震有利。
5 结 论
本文依托于济南市地铁建设拟建场地的地震安全评价工作,开展了典型土体的动三轴试验,并对试验结果进行了统计分析,进而给出了土体动剪切模量比和阻尼比随剪应变的变化规律,得到以下结论:
(1)对于同一土层,随着剪应变的增大,动剪切模量比减小,阻尼比增大;不过,试验结果离散性较大。
(2)采用动力本构模型对试验结果进行拟合分析,拟合效果较好,并获得了济南市区土体的动力本构参数。
(3)与其他地区研究成果比较,济南市区土体的动剪切模量比较大,阻尼比较小,说明其动力性质较好,对抗震有利。

