基于SVM的混凝土坝变形监控模型预测能力实例分析

，，，

(1.河海大学 a.水文水资源与水利工程科学国家重点实验室；b.水资源高效利用与工程安全国家工程研究中心；c.水利水电学院,南京 210098；2.雅砻江流域水电开发有限公司,成都 610051)

1 研究背景

鉴于SVM处理小样本、高维数、非线性问题的优势，SVM被应用到混凝土坝变形安全监控模型。文献[3]—文献[10]均采用SVM监测模型对大坝的变形和位移进行预报和监控，验证了基于SVM的监测模型的可行性与有效性。且与传统的统计模型相比，基于SVM的监控模型可有效提高拟合与预测精度。

文献[3]—文献[10]中模型对7～15不等数目的样本进行预测，预测样本个数的选取存在较大随机性和人为因素。为掌握基于SVM的混凝土坝变形监控模型的预测能力，本文应用实例分析探讨合适的预测样本数目和合理的预报模型。

2 基于SVM的变形监控模型

2.1 支持向量机SVM

支持向量机SVM被认为是目前针对小样本的分类、回归等问题的最佳理论，对样本数量的依赖性弱，能以任意精度逼近任意函数，可用于建立大坝变形与荷载、环境量、时效等之间的非线性关系。SVM的基本原理为利用核函数将训练样本从低维空间映射到高维特征空间，然后在高维空间内寻求最优线性回归函数[11]。

对于训练集(xi,yi),i=1,2,…,n,xi∈Rm,yi∈R，用非线性映射φ(·)建立向高维空间的映射，并构造回归函数,即

f(x)=wTφ(x)+b。

(1)

式中：w为权向量；b为常数。

以结构风险最小化为原则寻找w，b，寻优过程等价于式(2)。

式中：ξ为松弛变量；C为惩罚因子。

酒店员工职业认同对工作投入的影响研究——以三亚星级酒店为例 ……………………………………………… 王 洋（4/45）

为求解上述优化问题，引入Lagrange乘子αi，建立Lagrange函数,即

(3)

根据最优化理论转化为对偶问题，由KKT(Karush-Kulm-Tucker)条件：

(4)

可求得

(5)

消去w和ξi，并引入核函数K(xi,yi)，满足Mercer条件，可得到线性方程组[12]为

(6)

其中：

e=[1,1,…,1]T;α=[α1,α2,…,αl]T；

Qij=K(xi,xj) 。

式中Ι为单位矩阵。

可得回归模型为

(7)

2.2 模型建立及参数优化

监控模型一般包括训练集和预报集两部分，建立步骤如下：①利用训练集数据建立监测效应量与荷载之间的数学模型；②利用所得数学模型和预报期间的环境量测值得到效应量的预报值；③综合考虑建模误差和预报误差影响的前提下，对比预报值和相应时间的实测值以进行安全评估。

混凝土坝实测变形主要受库水位、下游水位、温度和时变因素的影响。因此基于以上思路，第1步，将水位因子、温度因子、时效因子作为SVM模型的输入向量，坝体变形值作为输出向量来学习训练，建立变形值与影响因子之间的非线性关系；第2步，将预报集实测影响因子输入到训练好的模型进行预报。SVM监控模型如图1。

图1 SVM监控模型Fig.1 Monitoring model based on support vector machine (SVM)

SVM模型的关键在于选取惩罚参数和核函数参数，其取值对模型性能有较大影响[13]。SVM模型采用交叉验证的方法选择参数，该方法在某种意义下可以得到最优的参数，有效地避免过学习和欠学习状态的发生。为实现对两参数的进一步优化,提高预测效果，常采用启发式算法对参数寻优[14]，包括遗传算法(Genetic Algorithm，GA)和粒子群优化算法(Particle Swarm Optimization Algorithm，PSO)等[11]，图2为PSO优化SVM参数算法流程。

图2 利用PSO优化SVM参数的算法流程Fig.2 Flow chart of algorithm optimizing SVM parameters by PSO

3 模型预测能力实例分析

某混凝土坝在厂1—厂8坝段322 m高程坝体纵向排水廊道布置1条引张线，用于监测坝体顺河向水平位移，引张线监测以2012年10月9日为基准日期。选取测点4EXC0801在2012-10-23—2015-12-21期间的监测资料建立大坝变形监控模型，一共191组实际观测数据。其中：a组数据用于拟合，即训练样本数目；b组数据用于预测，即预测样本数目。a，b的取值见表1。

表1 训练样本数目a、预测样本数目b取值方案Table 1 List of values for training sample number a and prediction sample number b

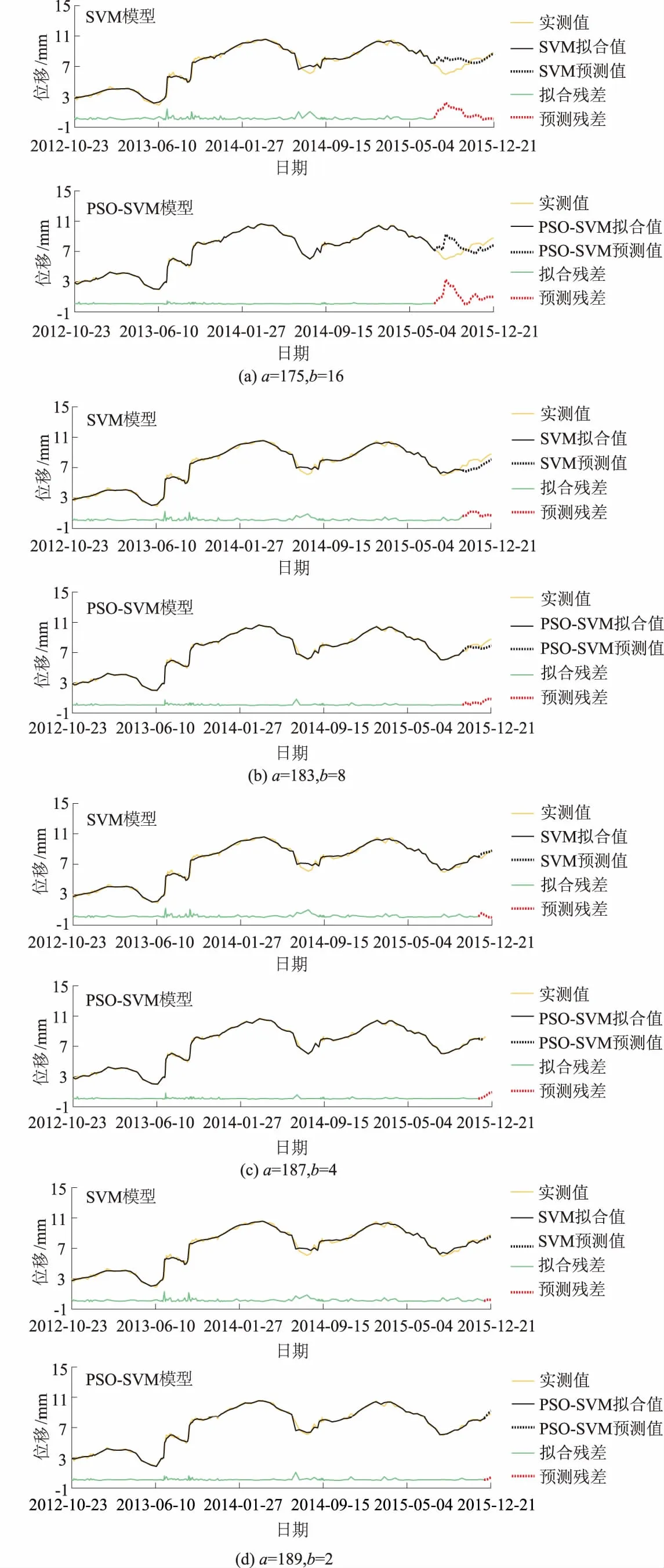
图3 SVM模型与PSO-SVM模型拟合曲线与预测曲线Fig.3 Fitted curves and forecast curves of SVM model and PSO-SVM model

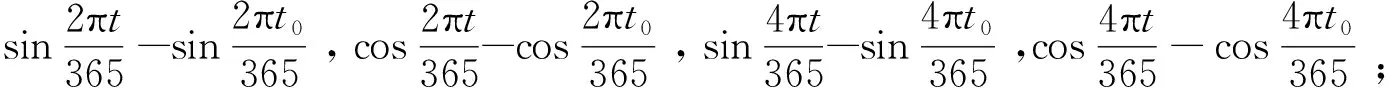
建立基于支持向量机的混凝土坝变形监控模型(SVM模型)和粒子群优化算法的改进混凝土坝变形监控模型(PSO-SVM模型)，对测点4EXC0801监测数据进行拟合和预报。图3为a=175,b=16;a=183,b=8;a=187,b=4;a=189,b=2方案下SVM模型与PSO-SVM模型的拟合曲线与预测曲线，可见：同一b取值下，PSO-SVM模型拟合残差曲线比SVM模型拟合残差曲线更平滑，2类模型预测残差曲线均比拟合残差曲线波动大，且2类模型预测残差曲线波动变幅几乎在同一水平；随b取值的减小，2类模型预测残差曲线波动减弱，逐渐趋于平缓。

利用预报值与真实值的均方差定量评估模型的预测能力，位移均方差FMSE表达式为

(8)

16种预测样本数目取值方案下SVM模型与PSO-SVM模型回归FMSE与预测FMSE曲线如图4所示，部分取值方案下的SVM模型与PSO-SVM模型回归FMSE与预测FMSE的值统计于表2。结果显示，预测样本数目b取不同值时，2类模型回归效果几乎维持在某一水平，变化微小，SVM模型回归FMSE均值为0.31 mm，PSO-SVM模型回归FMSE均值为0.16 mm，PSO-SVM模型回归FMSE均值小于单纯的SVM模型，表明PSO-SVM模型回归效果更优；随着预测样本数目b的减小，2类模型预测FMSE整体上呈下降趋势，可见2类模型近期预测能力普遍优于远期预测能力；预测样本数目b取值相同时，PSO-SVM模型和SVM模型的预测FMSE不存在明显的优劣势，在一定程度上说明训练样本数目b的取值对模型预测精度的影响要大于参数优化带来的影响。

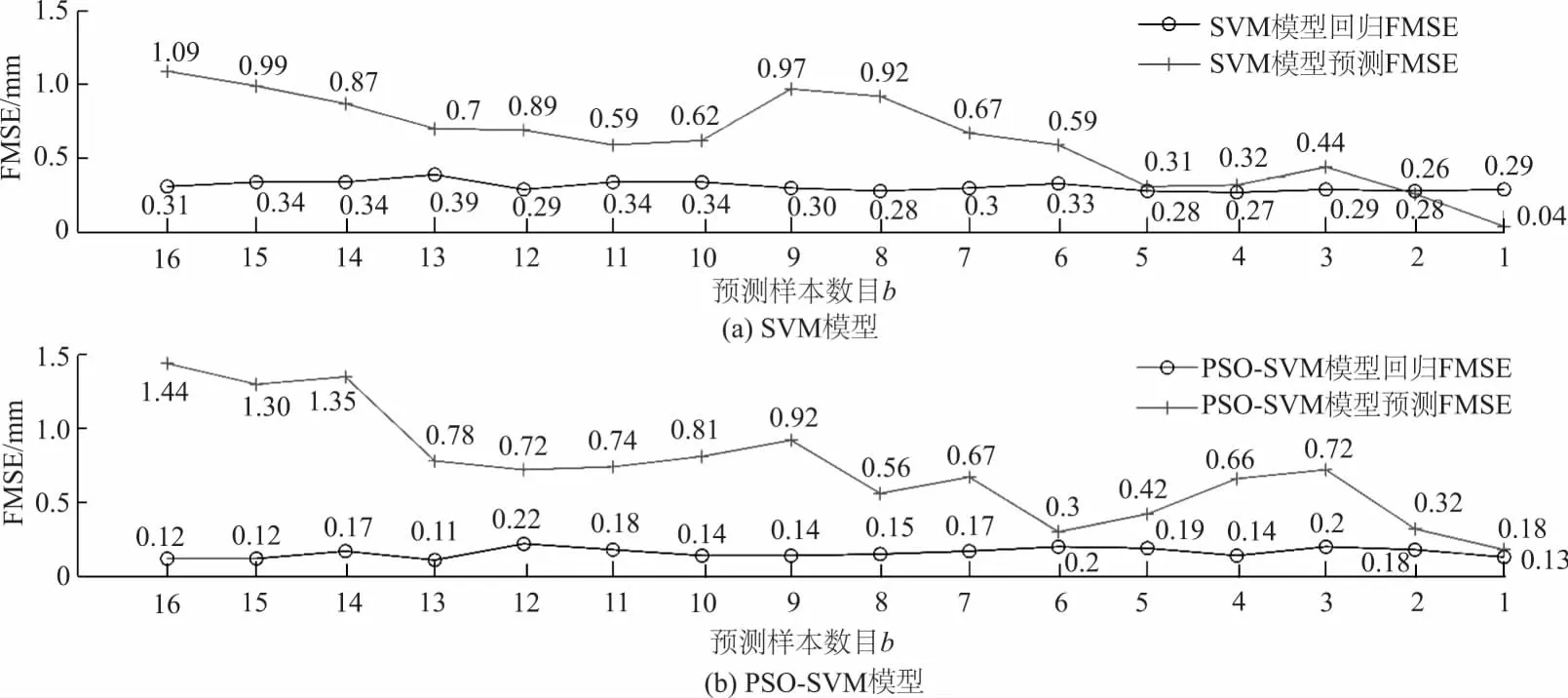
图4 不同预测样本数目下SVM与PSO-SVM模型回归FMSE与预测FMSE变化曲线Fig.4 Curves of regression FMSE and forecast FMSE of SVM model and PSO-SVM model with varying number of prediction sample

取值情况回归FMSE/mm预测FMSE/mmSVM模型PSO-SVM模型SVM模型PSO-SVM模型b=160.310.121.091.44b=80.280.150.920.56b=40.270.140.320.66b=20.280.180.260.32平均值(b=1,2,…,16)0.310.160.630.74

4 结 语

针对某工程实例，选取不同数目的预测样本建立基于SVM和PSO-SVM的混凝土坝变形监控模型，通过分析预测样本数目不同取值方案下模型预测值与真实监测值的均方差，探讨监控模型的预测能力。实例分析表明：

(1)SVM模型和PSO-SVM模型均具有良好的适应性和非线性拟合性，可用于大坝变形安全监控。

(2)基于SVM和PSO-SVM的变形监控模型短期预测能力优于长期预测能力。

(3)基于SVM的变形监控模型预测能力受训练样本数目的影响大于算法优化带来的影响，表明选择合适数目预测集对合理有效预报尤为重要。

本文对基于SVM的变形监控模型预测能力的研究具有一定的应用价值，可为建立有效的基于SVM的混凝土坝变形监控模型提供参考和依据。