含积分风险的电网经济调度研究*
韩丽,李明泽,史丽萍
(中国矿业大学 电气与动力工程学院,江苏 徐州 221008)
0 引 言
随着全球日益严重的资源短缺和环境恶化,风能作为一种“取之不尽,用之不竭”的可再生能源,得到人们的重视和开发。风力发电除了必要的投资和成本维护之外不需要任何花费,对环境无污染,具有经济和环保两方面的优势。但由于风电的随机性和不确定性,导致含风电电网调度与传统调度方式有很大区别。含风电的电网调度由于风电机组的参与,调度中风电机组相对于预测发电不足或者过多造成的弃风现象时常发生,故需要考虑风险成本和旋转备用量等因素。
对于含风电机组的电网调度,国内外学者针对这一课题做了广泛研究,文献[1-3]将风电机组的预测功率作为实际发电量或预留固定百分比的旋转备用容量,称为确定性建模。但由于风电的不确定性,预测值通常有偏差,导致最终调度结果误差较大。除上述方法外,文献[4-5]采用模糊建模隶属函数的方法来解决电网调度问题,但此类方法太依靠于决策者的主观判断,容易偏离实际。由于风电的预测难度较大,许多学者通过风速或风电功率密度分布函数建立数学模型[6-10]。文献[6-7]认为风电概率符合Weibull分布。文献[8]假定风速概率符合Rayleigh分布,并采用对概率密度积分的方法建立含电动汽车和风电低估和高估风险的数学模型。文献[9]假设风电功率归一化处理之后服从Beta分布,引入正负旋转备用容量将概率机会约束随机调度转化为确定性模型。文献[10]对风电预测采用直接统计的方法,认为风电功率服从预测值为均值,预测误差为标准差的正态分布。然而这些方法将风电功率概率分布假设为一个固定的函数,而风电的功率输出受气象、安装位置、季节、设备等诸多因素的影响,采用固定函数拟合风电功率概率分布误差较大。
由于风电的优化调度具有非线性、高维离散和多约束等特点,文献[11-12] 用智能优化算法来解决电网调度问题。文献[12]为减少弃风,提出了一种限制风电功率运行的调度方案,并用遗传算法来进行求解。为了解决复杂电网调度问题,文献[13]用GAMS软件平台调用CPLEX求解器求解。除智能算法和CPLEX软件之外,文献[14]提出了一种改进的拉格朗日松弛法,解决含风火储能装置的数学模型的经济成本问题。
通过分析风电机组的历史发电数据,建立动态的风电功率概率密度分布函数,然后将该概率分布以积分的形式引入到电网调度的目标函数中,建立了基于积分风险的调度模型,并提出了改进的骨干粒子群算法(I-BBPSO),实现对调度模型的求解与分析。
1 风电机组发电功率概率分布
对于不同时间、地域、风电机组的功率概率密度分布函数也不同。图1是美国德州某风电机组在不同时间段的发电量概率分布[15],其中柱状图表示实测风机机组的功率频率,根据风电数据拟合成风电功率概率密度分布函数如图1曲线所示。
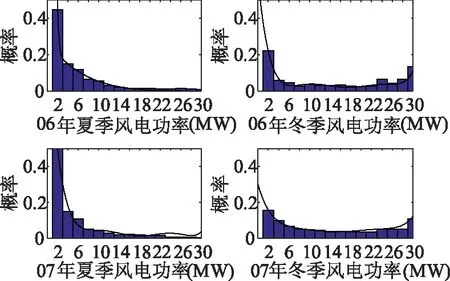
图1 某风电机组在不同年夏冬下午3时功率概率分布Fig.1 PDF of wind power at 3 pm in summer and winter
通过图1发现,风电机组在夏季和冬季的功率概率分布差别较大,风电功率密度分布是一个不确定的动态函数,故在调度模型中采用固定概率分布会带来较大误差。因此,需要在调度过程中根据所选择的数据拟合成契合的风电功率密度分布函数。
为了获得风电功率概率分布动态模型,实时拟合当前的概率分布函数。图2为同一风电机组不同时刻的功率频率,将6,12,18和24时拟合成的功率分布函数分别为高斯函数、傅里叶函数、多项式函数和幂函数。
拟合风电功率概率分布函数,即:
pwi=f(wi)
(1)
式中f(wi)为风电功率概率拟合曲线;wi为第i台风电机组的预测值定义域为[wimin,wimax],wimax和wimin为风电机组出力上下限;pwi为风电机组在发电功率等于wi时的概率值。当风电功率预测值wi大于(小于)实际功率时,pwi表示风电高估(低估)概率。将pwi引入到调度模型中,可求得风电机组的低估和高估风险。
2 含积分风险的数学模型
2.1 火电机组和风电机组成本
含风电机组的电网调度成本,如下:
minf(t)=F(t)+E(t)+S(t)+R(t)
(2)
(3)
(4)
(5)
式中f(t)表示电网调度总成本;F(t)和E(t)为第t时段火电机组的燃料成本和废气排放成本;S(t)和R(t)为第t时段的风电机组的运行维护成本和风险惩罚成本;N为系统火电机组的数目;Pi为火电机组第i台的发电功率;ai,bi和ci为给定费用系数;kp为废气排放处理价格系数;di和fi为阀点效应系数;αi,βi,γi,ξi和λi分别为给定的废气排放系数;Cwi为第i台风电机组的运行维护成本系数;Wi为第i台风电机组的实际功率;M为风电机组的数目。
风电机组的风险惩罚成本包括风电功率预测低估(弃风)惩罚成本和高估(失负荷)惩罚成本。
(6)
式中Wi,av为第i台风电机组的预测功率;Cui和Coi为第i台风电机组的低估和高估惩罚因子。引入惩罚因子可以将风电的不确定性体现在函数上,容易用数学的方法进行优化。积分风险是指将风电功率范围分为低估区间和高估区间,两个区间均有对应的惩罚系数。通过积分运算可以得到低估(高估)的加权平均功率,其中加权值为低估(高估)功率概率pwi。然后将预测功率Wi,av与低估(高估)加权值作差,得到低估(高估)功率差值和低估(高估)的惩罚成本。这种计算惩罚成本,可以降低预测偏差较大所带来的误差,使计算结果更符合真实情况。
2.2 模型的约束条件
由于风电机组由于具有随机性,其约束条件主要由等式和不等式组成,其具体约束条件如下:
(1)功率平衡条件
Pc=Pf+Pw
(7)
式中Pc表示负荷需求功率。
(2)火电机组出力约束
Pimin≤Pi≤Pimax
(8)
式中Pimax和Pimin表示火电机组的出力上下线。
(3)风电机组出力约束
0≤Wi≤WN
(9)
式中Wi和WN表示风电机组的实际功率和额定功率。
(4)机组爬坡速率约束
-φdowni,t≤Pi,t-Pi,t-1≤φupi,t
(10)
式中φdowni,t和φupi,t在t时刻和机组出力的爬坡率。
(5)正负旋转备用容量约束
(11)
式中ui为火电机组的启停状况,0为停机1为开机;L%为负荷对正、负旋转备用的需求系数;sp%和sm%为风电预测功率对正负旋转备用的需求系数。
3 改进的骨干粒子群算法
提出的电网调度模型中含有动态积分量,风电功率概率密度曲线的动态调整也会带来模型的变化,因此对优化算法的计算速度要求更高。为此利用遗传算法中变异交,对骨干粒子群算法加以改进。用改进的算法(I-BBPSO)对模型加以求解和分析。
骨干粒子群算法(BBPSO)是利用利用高斯分布对每个粒子个体极值点和全局极值点的加权平均值,完成对微粒位置更新。根据文献[16],有:
(12)
式中xi,j(k+1)表示第i个粒子在k+1代的位置;pi,j(t)和pg,j(t)表示第i个粒子在k代的个体极值和全局极值;N(·)表示高斯分布。式(14)有50%的机会改变下一代粒子的位置,但骨干粒子群仍有易于早熟收敛不足和陷入局部最优值等缺点。
为保证种群的多样性和不易收敛于局部最优解,对骨干粒子群算法加以改进,引入遗传算法,通过对骨干粒子群算法加以改进,引入遗传算法,通过对种群中部分个体进行变异选择操作,具体如图3所示。I-BBPSO不易收敛于局部最优解,在迭代数和精度上优于普通粒子群算法和骨干粒子群算法。
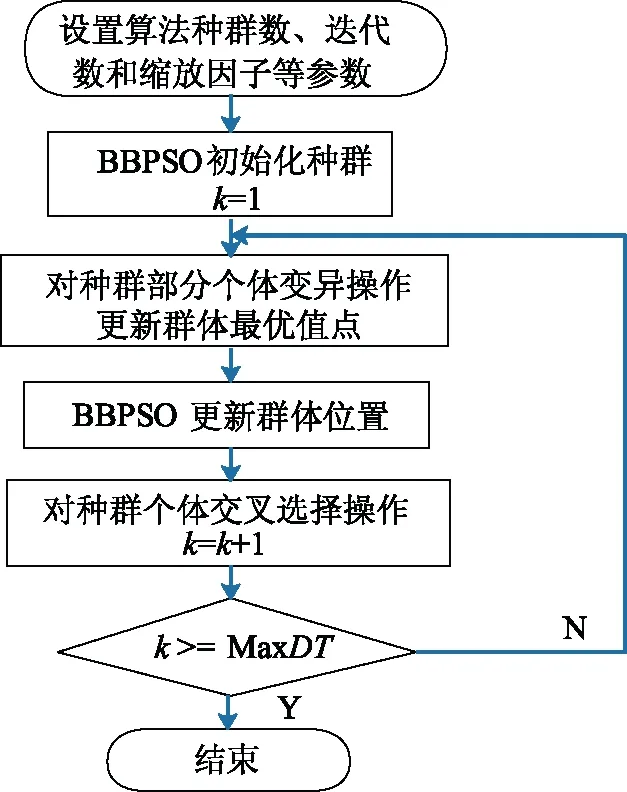
图3 改进的骨干粒子群(I-BBPSO)算法流程图Fig.3 Flow chart of I-BBPSO algorithm
4 算例分析
4.1 基于数学模型的I-BBPSO算法分析
选取IEEE30节点中各参数如表1所示[17]。风电场发电机组的相关系数见文献[11],如表2所示,其中风电机组和火电机组的出力单位是100 MW。
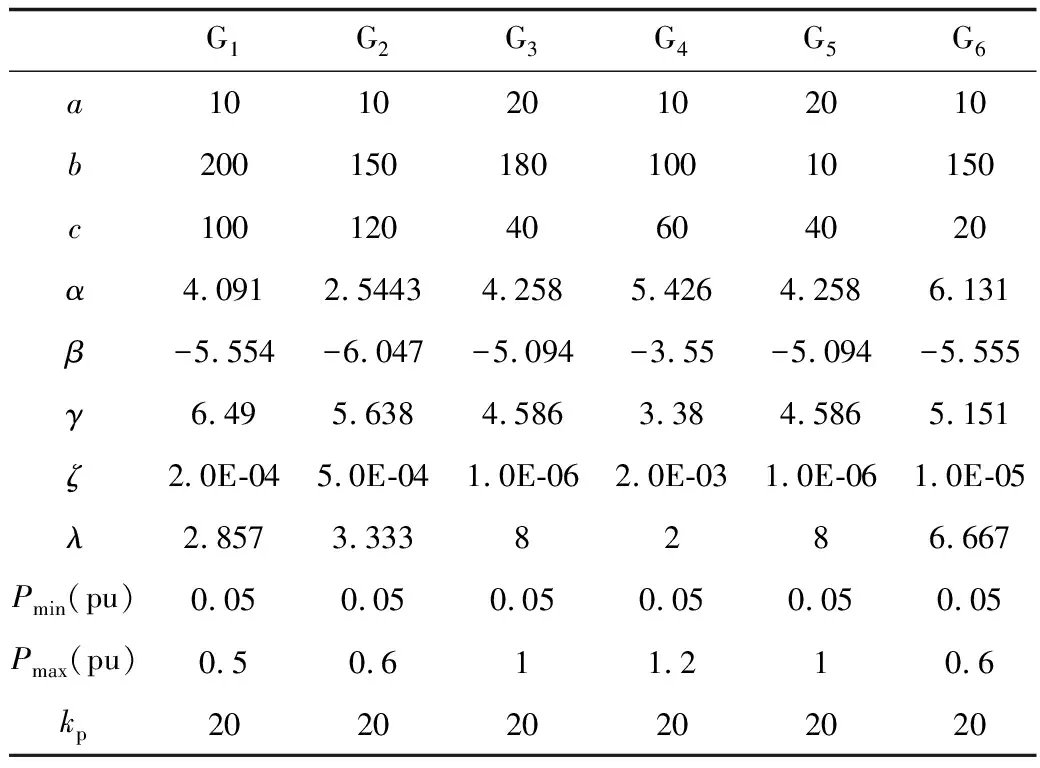
表1 火电机组发电的相关系数Tab.1 Correlation coefficient of thermal power generation
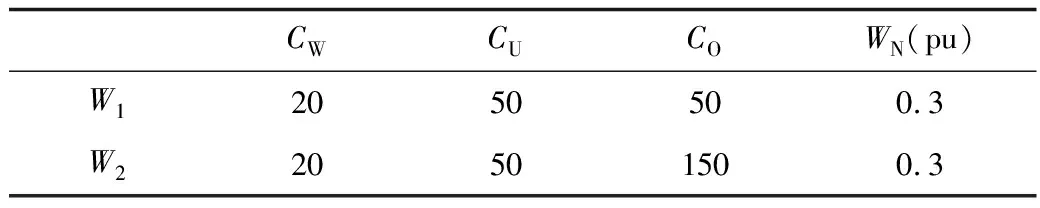
表2 风电机组发电的相关系数Tab.2 Correlation coefficient of wind power generation
I-BBPSO算法控制参数如下:种群规模为100,最大迭代数为1 000,独立循环10次。各时段负荷要求和风电机组的预测功率如表3所示。
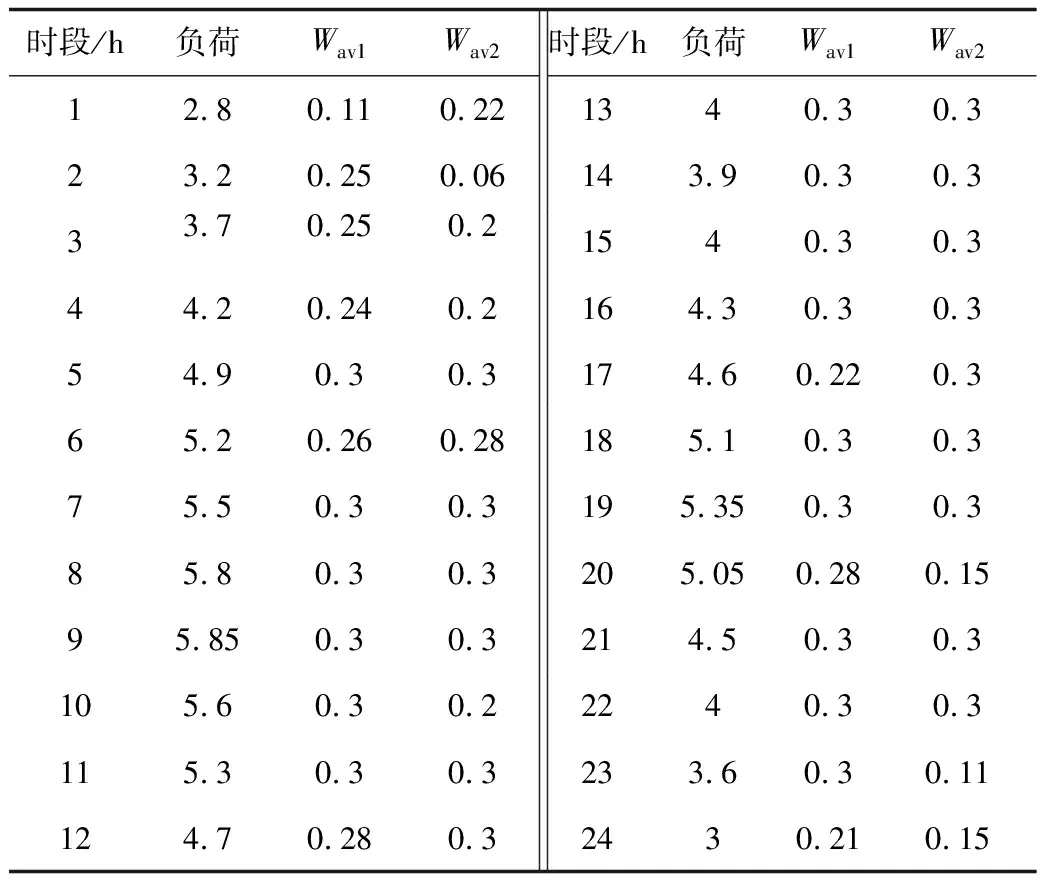
表3 各时段负荷要求和风电机组的预测功率(pu)Tab.3 Load and wind forecast power in each time(pu)
将文献[18]中传统调度模型带入到I-BBPSO和其他算法中进行了对比分析如表4所示,其中用I-BBPSO得到的风电功率如表5所示,各个机组发电情况如图4所示。
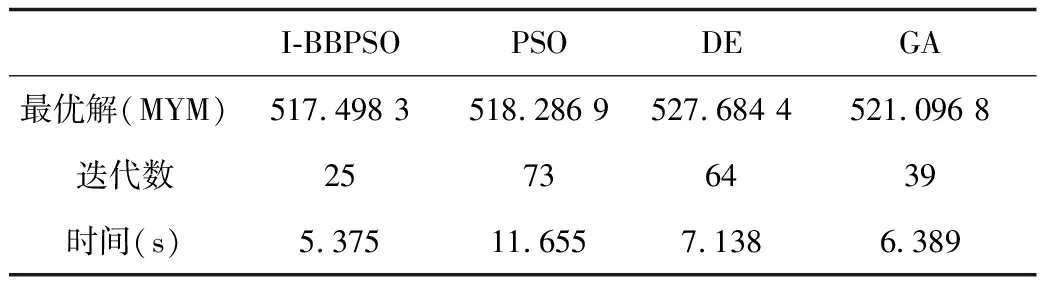
表4 在4时刻I-BBPSO和其他算法比较Tab.4 Comparison of I-BBPSO and other algorithms
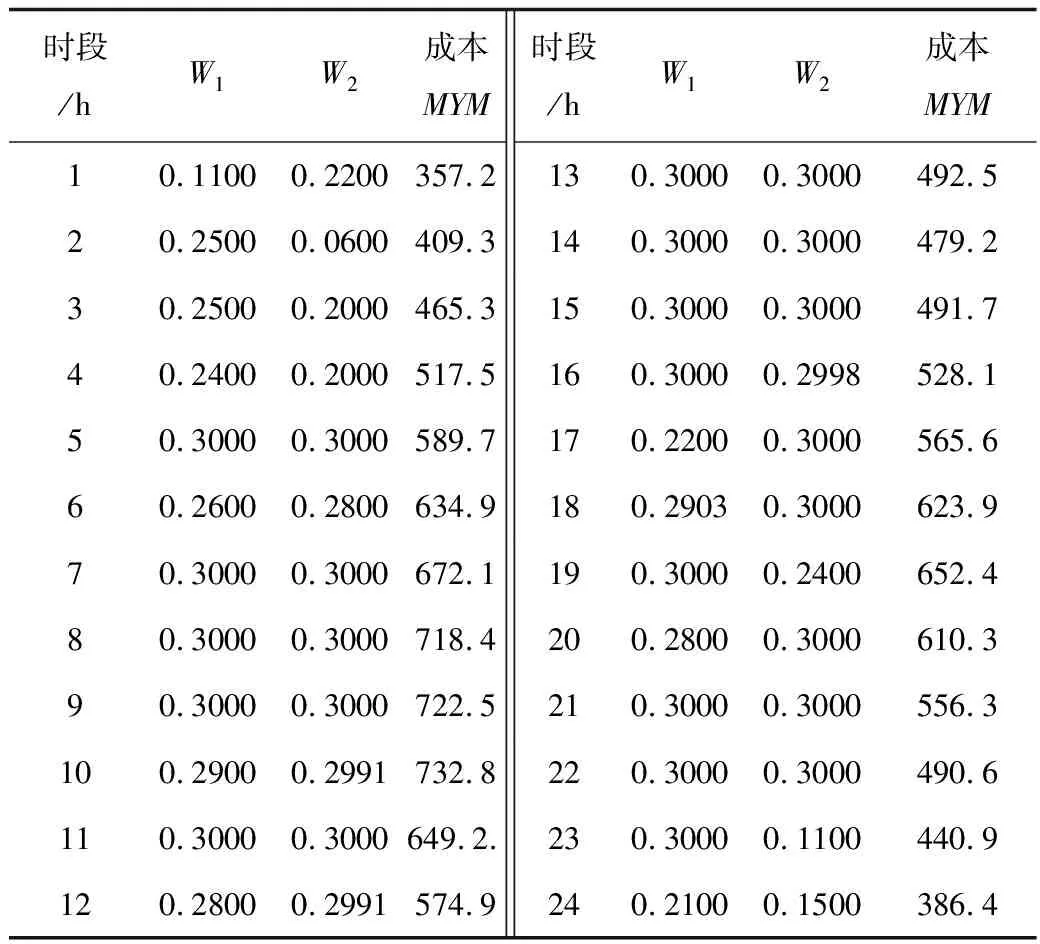
表5 I-BBPSO传统调度模型风电机组的输出功率(pu)Tab.5 Output power of traditional scheduling model of unit(pu)
通过图4和表4比较分析,发现对于求解电网调度模型时,I-BBPSO在求解结果要优于其他算法,可以将改进的算法对新提出的数学模型进行求解。
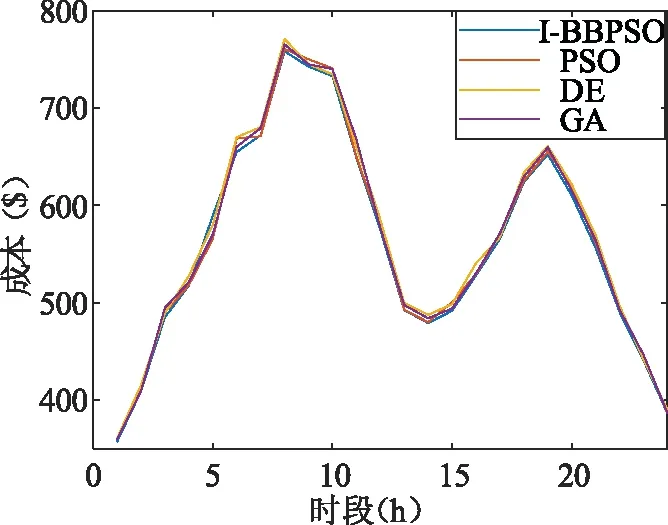
图4 I-BBPSO传统调度模型风电机组的输出功率(pu)Fig.4 Output power of traditional scheduling model of unit(pu)
4.2 含风电的经济调度分析
采用美国某两个风电场某周内发电功率数据作为研究对象。根据风电场各个时段的数据将其拟合成动态分布函数,拟合成函数如下:
式中af,bf,ag,bg,cg和ap表示风电功率概率分布的参数。其中德州风电场功率概率在1,2,6,7,10,11,18,20,22时段服从傅里叶函数分布;在3,5,9,13,15,21,24时段服从高斯函数分布;在4,8,12,14,16,17,19,23时段服从多项式函数分布。
文中选取在1时段,3时段和4时段时德州风电场概率分布做代表性分析。时段1为傅里叶函数分布,其参数f=3,af=[1.1e+12,-1.6e+12,-2.28e+11,2.82e+10],bf=[-9.82e+10,9.81e+10,-4.19e+10,6.96e+09],w=[0.003 8];时段3为高斯函数分布,其参数如下:g=2,ag=[0.44,0.045,2.03e+13],bg=[-0.44,2.87,987.4],cg=[1.08,6.9,163.4];时段4为多项式函数分布,其参数p=6,ap= [6.39e-08,-6.49e-06,0.000 26,-0.005 3,0.056,-0.29,0.62]。
将文中提出新的数学模型带入到I-BBPSO算法中得到火电厂和风电场发出的有功功率如表6所示。
在表6中可以看出,G5因为发电成本参数较低,所以在任何时段中几乎满载发电,同理G6也保持在0.6 pu左右。负荷要求最高的时段在7时~12时和17时~21时,在此时段的经济成本也最高。在这些时段为满足发电需求,G3和G4提供比其他时段更多的功率。而G1和G2由于发电成本较高,所以发电量以及发电变化量较小。W1由于惩罚因子较低所以在整个时段中发电量都很大,尤其在负荷要求较大时W1大多数时段实际值与预测值相近。风电机组相比于火电机组,发电量较低时风电机组发电成本较低更经济。当风机机组发电量较大时,风险成本增加,导致电网调度的成本也会增加。由于W2的惩罚因子较高,故W2有时在要求发电负荷增加时,会出现实际发电值小于预测值,甚至发电量反而减小的情况。
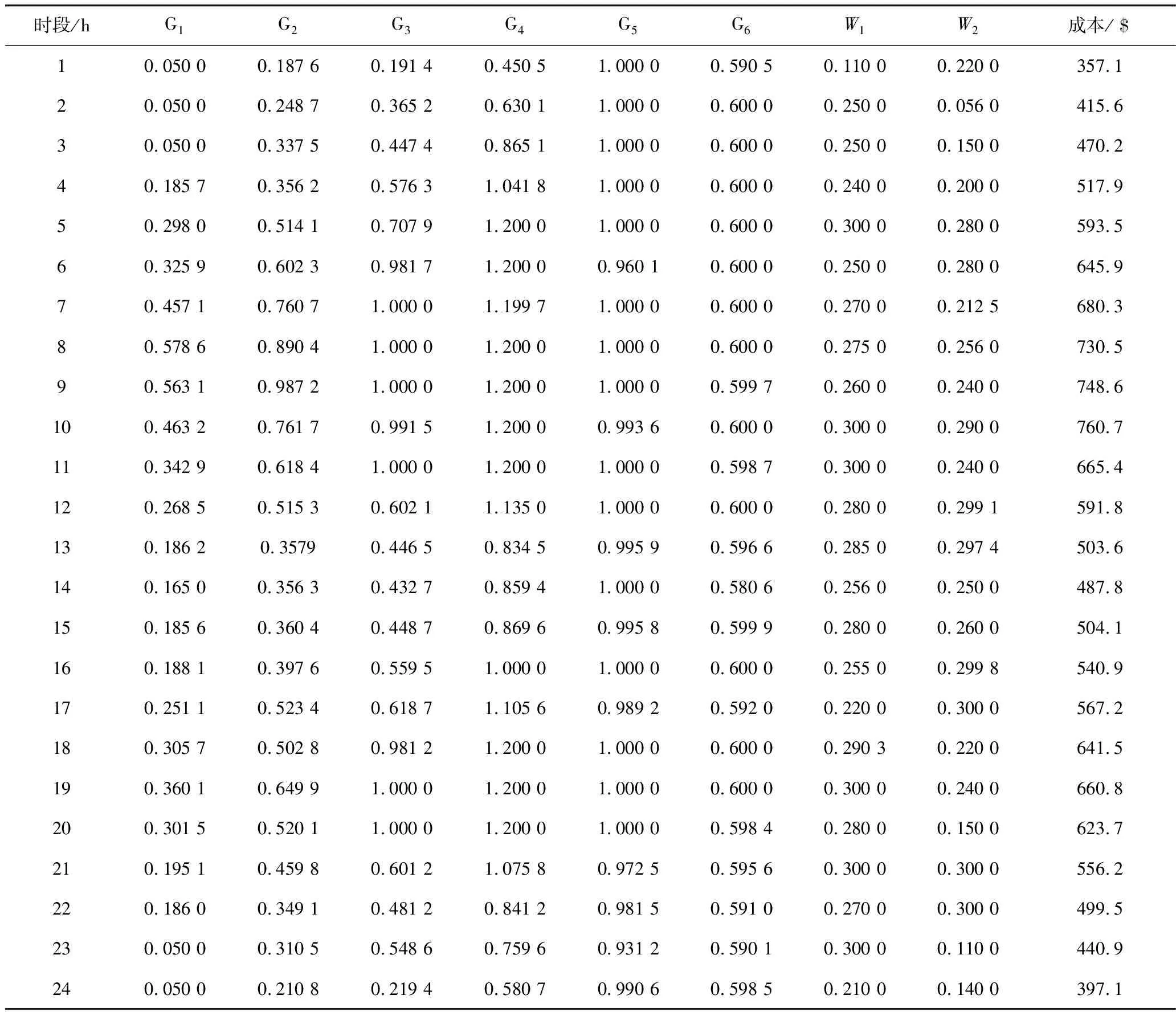
表6 含积分风险的调度模型中火电机组和风电机组的输出功率(pu)Tab.6 Output power of the thermal power unit and the wind power unit in the model with integrated risk(pu)
表7中可以看出,在7~9,14~15时段风电的预测功率为额定功率。以W1为例,积分模型在7~9,14~15时刻的发电量是0.212 5,0.256 0,0.240 0,0.250 0和0.260 0,而传统模型按额定功率输出。积分模型下W1和W2实际发电量未达到预测发电量的次数比传统多很多,故其发电成本比传统模型要高。但由于本文建立的模型中考虑了风电输出概率,以7时为例,而W1功率概率分布如图5所示,在功率满发概率很低,而在功率为0.2时概率较大,故积分风险模型中W1在此时刻的功率为0.212 5,虽然在计算中增加了成本,但避免了风电在低概率发电量下对电网带来的风险。
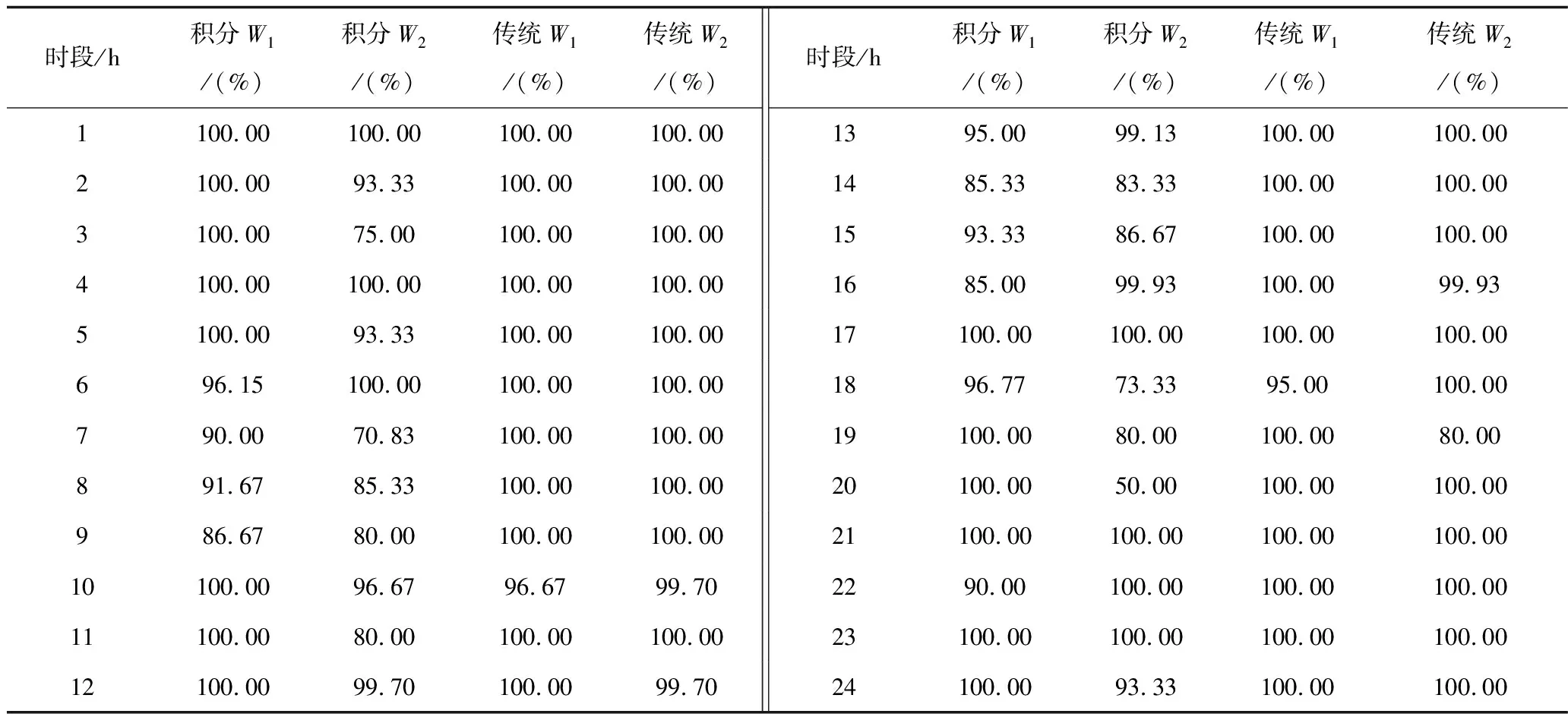
表7 在含积分风险和传统调度模型中风电机组实际输出功率与预测功率的比值Tab.7 Ratio of the output power and the predictive power in the integrated risk and the traditional model

图5 7时段W1风电功率概率分布曲线Fig.5 7 periods wind power probability curve of W1
5 结束语
通过分析风电机组的发电功率概率拟合了风电机组功率概率曲线,得到了不同情况下动态的风电功率密度函数,积分计算了基于概率分布动态函数的风险成本。然后建立了基于积分风险的电网经济调度模型。同时提出了利用遗传算法改进的骨干粒子群算法(I-BBPSO)。通过验证证明了改进的骨干粒子群算法(I-BBPSO)提高了粒子的收敛速度和计算精度。最后采用IEEE30节点的火电机组和美国某两个风电场对所提出的基于风险的模型进行计算与分析,分析结果表明该模型能够兼顾风电的发电成本和发电概率,降低风电在低概率发电输出工况时对电网运行的冲击。

