基于小波自适应阈值滤波的VMD降噪方法*
唐圣学,付滔,张雪辉
(河北工业大学 电气工程学院,天津 300130)
0 引 言
非稳态信号中细节部分蕴含着大量有用信息,在进行降噪处理时希望保留这部分有用的细节信息。傅里叶变换降噪方法不能很好地刻画非线性信号的局部细节信息,不适合处理非线性非平稳信号降噪;小波变换在时频域内都有较强的信号局部特征表征能力,但阈值及阈值函数选取会影响降噪效果。
近年来,基于模态分解的非线性非平稳信号降噪方法得到了快速发展,如经验模态EMD降噪、局部均值LMD降噪以及其改进方法降噪等。EMD[1-2]分解方法能将信号按局部时间的特征尺度自适应地将信号从高频到低频顺序分解成一组尺度不同的固有模态函数,用于降噪时通常采用舍弃EMD分解的高频IMF分量、由低频IMF分量重构达到降噪效果,但可能会失去高频IMF分量含有的有用信息。LMD分解降噪原理与EMD类似,且对噪声敏感[3-5]。为了提高EMD降噪效果,文献[6]提出了基于Savitaky-Golay滤波器的一种改进的EMD-SG降噪方法。
2013年,Dragomiretskiy[1]等人提出了变分模式分解(Variational Mode Decomposition,VMD)[2-3]的自适应分解方法,解决了EMD 和LMD在递归模式分解过程中的模态混叠、对频率相近的分量无法正确分离、受采样频率影响等缺点。由于VMD解决了EMD和LMD在递归模式分解过程中的模态混叠、对频率相近的分量无法正确分离、受采样频率影响等缺点。
提出一种基于VMD和自适应小波阈值函数降噪方法,该方法结合了小波自适应阈值技术和VMD分解技术,能对多类信号进行有效的降噪。通过数值实验表明:该方法对非平稳降噪具有良好的降噪效果,且适应性广。
1 变分模式分解
1.1 VMD基本原理
与EMD分解相同,VMD算法也将信号分解为本征模态IMF分量;不同之处在于VMD在分解过程中避免了EMD的循环筛分剥离获取IMF分量的处理方式,而是将信号分解获取IMF过程转化为变分求解过程,即分解问题转移变分框架内处理,通过搜寻约束变分模型最优解实现信号自适应分解获取IMF分量[7-10]。VMD原理简述如下:
假设原始信号f分解成k个IMF分量,则对应的约束变分模型为:
(1)
式中uk为第k个模态分量;ωk为模态分量的中心频率,k=1,2,3…,K。为了求解上述约束变分问题的最优解,将约束性变分问题转变为非约束性变分问题。引入二次惩罚因子α和Lagrange乘法算子λ(t),得到增广的Lagrange表达式为:
(2)
VMD分解算法具体过程如图1所示。
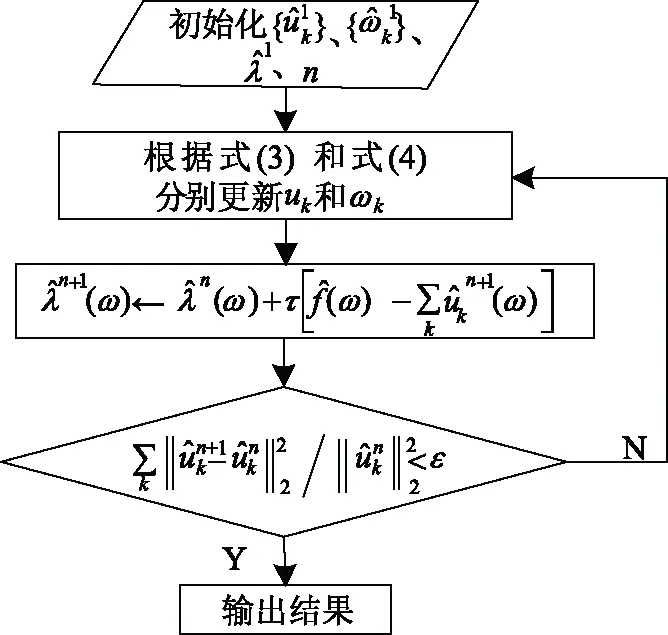
图1 VMD的具体实现[4]Fig.1 Concrete implementation of VMD algorithm
利用交替方向乘子法(ADMM)迭代搜索上述扩展的拉格朗日函数的鞍点,即式约束变分模型的最优解,所有模态分量uk为:
(3)
(4)
1.2 VMD分解实例
含噪声的多频信号x(t)如下:
(5)
式中η代表噪声信号,设信噪比SNR=5 dB,信号时间为1 s,采样频率1 kHz。图2给出多频信号x(t)及其分解结果。
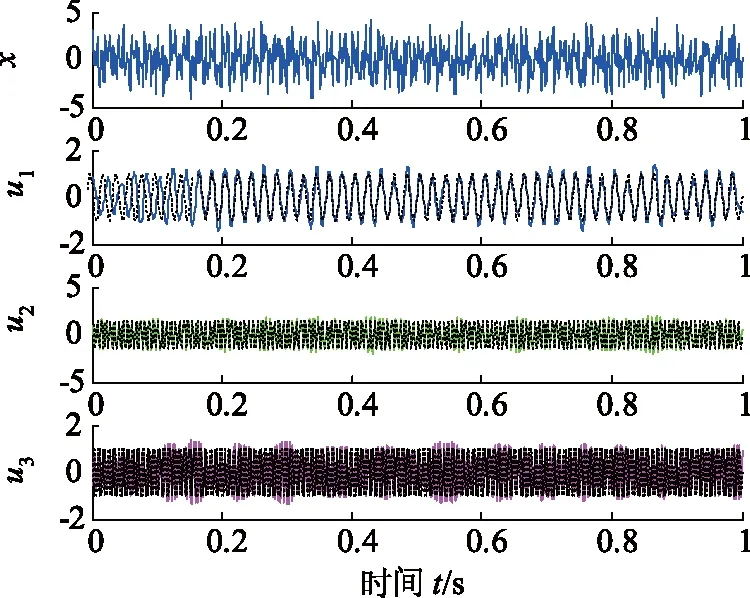
图2 多频信号分解Fig.2 Decomposition of multi-frequency signal
由图2可见,VMD分解后IMF分量按照频率由低向高依次递增,IMF分量频率单一,分解效果好;同时,高频IMF分量中噪声含量大,VMD分解后噪声主要集中在高频段。对各个分量进行FFT变换,得到如图3所示的IMF分量频谱。由图3可见,u3分量频谱带宽内集中了信号的大部分噪声能量。
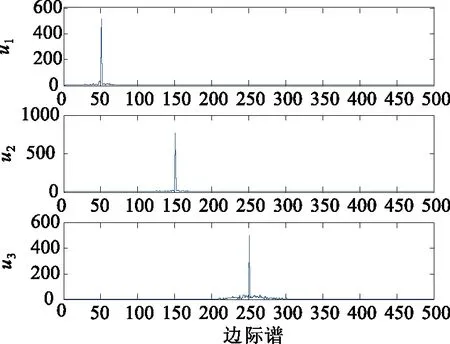
图3 VMD各分量边际谱Fig.3 VMD marginal spectrum of each component
2 基于VMD与自适应小波阈值函数降噪原理
如果能降低高频IMF分量中噪声,在通过与低频分量重构,就可以减低原始信号噪声,这即是文中的降噪原理。小波变换具有表征信号的时频特性,能很好降低信号噪声。文中选用小波变换降低高频IMF分量中的噪声。
小波降噪过程分为三步[11]:(1)对含噪声的信号进行小波变换;(2)保留最大尺度下的低通滤波分量,对其他尺度分量进行降噪处理,即根据设定阈值函数和阈值对其进行自适应处理;(3)对处理后的小波系数进行小波逆变换,获得降噪后的估计信号。
小波降噪效果好坏的关键是选择合适的阈值函数与最佳阈值[12]。目前,硬阈值和软阈值是常见的两种阈值函数。硬阈值函数因在阈值处函数不连续,容易造成缺乏像原始信号的光滑性;软阈值函数虽连续性较好,但存在恒定的偏差。文中采用文献[13]提出的一种自适应阈值函数,既能降低噪声又保留了信号原有的奇异性,选用的自适应阈值函数为:
(6)
式中th为阈值;m为可调参数,可取大于1的连续实数。m决定了函数η(·)形状、性质。当m接近于1时,类似于软阈值函数;当m>10时,类似于硬阈值函数。
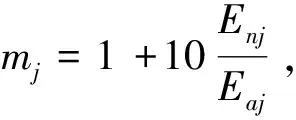
在阈值获取方面,该文献提出的方法存在一些问题,文中阈值基于数据SURE无偏估计自适应获得。
基于自适应小波阈值的VMD降噪方法如图4所示。先对原始信号进行VMD分解得到模态分量,然后对含噪声分量大的高频模态分量进行小波自适应阈值滤波,最后将滤波后高频模态分量和低频模态分量重构即得降噪后的信号。需要指出的是:对于高频分量是否需要降噪处理,可由各模态归一化自相关函数判断。
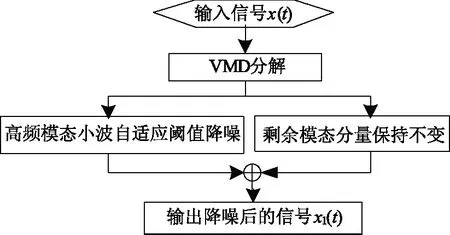
图4 文中降噪流程Fig.4 De-noising process in this paper
3 仿真实例
为了说明所提出方法的降噪效果,下面选用3个典型的含噪声信号进行降噪数值仿真,3个信号分别为多成分信号、Doppler信号和调制信号,降噪效果评价指标为信噪比(SNR)、和均方根误差(RMSE)。
3.1 多频信号
针对式的含噪声的多频信号,图5给出了降噪后的重构波形,同时还给出了采用传统EMD方法降噪波形、EMD-SG方法降噪波形、EMD-WT方法降噪波形、小波方法和文献方法波形。降噪性能指标如表1所示。上述其他5种降噪方法中,EMD方法采用舍弃部分高频IMF分量的传统EMD去噪方法;EMD-SG方法过程可参考文献[6]和EMD_WT方法可参考文献[7];小波方法采用symN小波系,分解层数为5,阈值选取基于MinMax极大极小值规则处理。
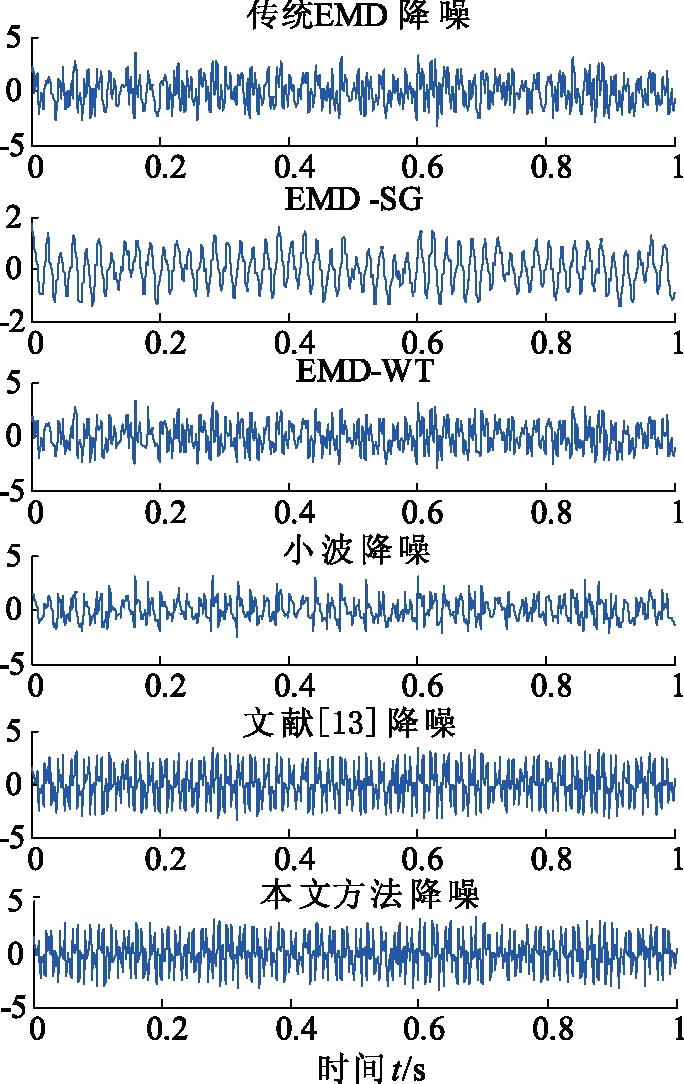
图5 含噪声的多频信号降噪波形Fig.5 De-noising waveform of multi-frequency signal with noise
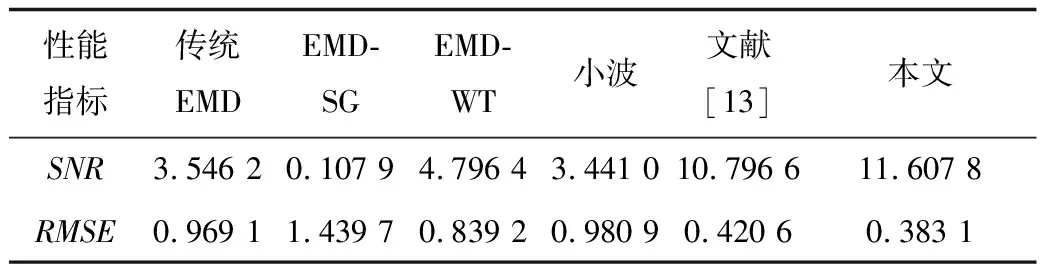
表1 多频信号降噪效果Tab.1 De-noising effect of multi-frequency signals
3.2 Doppler信号
图6给出了Doppler信号和含噪声的Doppler信号,含噪声信号SNR为5 dB,信号采样点数为1 000。图7给出了6种方法降噪后的波形图,表2给出了降噪性能指标。
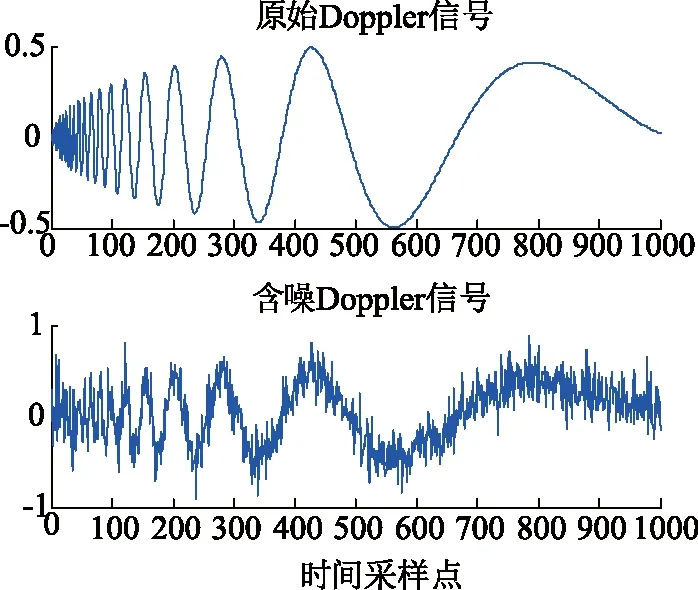
图6 Doppler信号Fig.6 Doppler signal
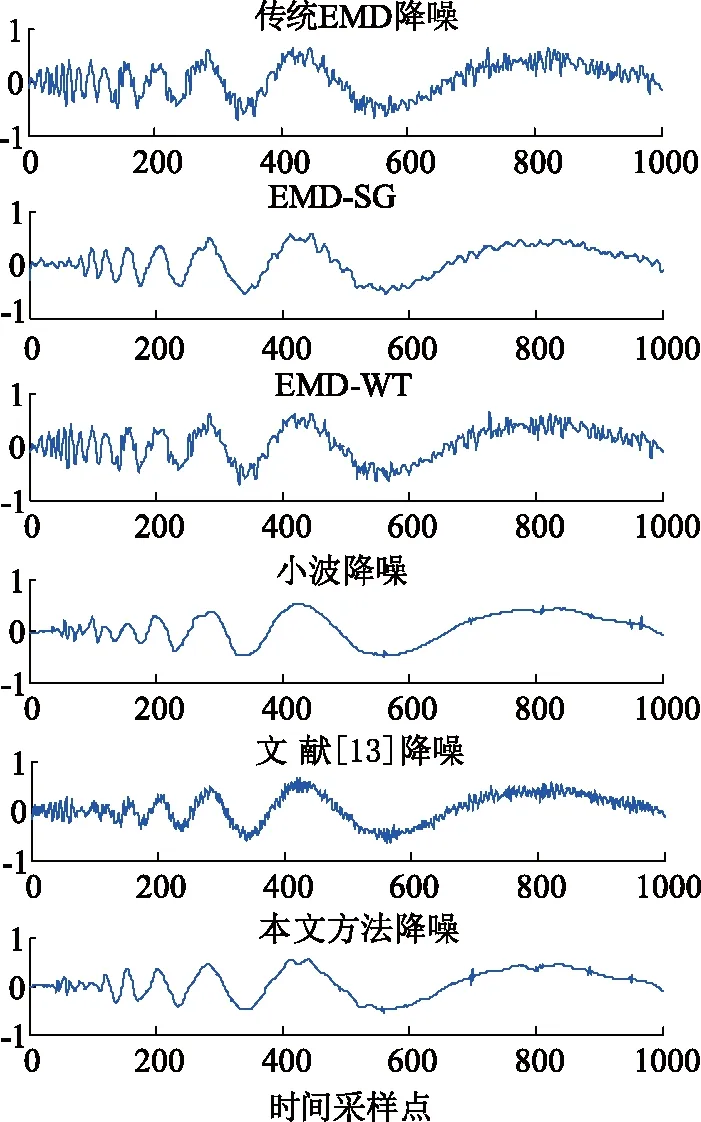
图7 含噪声的多频信号降噪波形Fig.7 De-noising waveform of multi-frequency signal with noise
由图7可见,EMD-SG方法和小波方法与文中方法降噪效果差不多;由表2可见,对于Doppler信号降噪,文中方法降噪性能指标略优于EMD-SG方法和小波方法。说明文中方法能有效降低Doppler信号中的噪声。
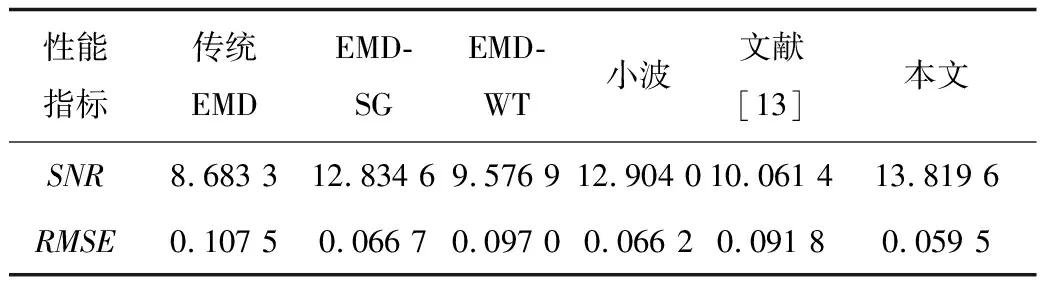
表2 Doppler信号降噪效果Tab.2 De-noising effect of Doppler signals
3.3 调制信号
为了进一步EMD-SG方法和小波方法与文中方法降噪效果,对如下调制信号进行降噪处理,调制信号为:
y(t)=0.45[1+25sin(30πt)]sin(160πt)+η
信号采样频率为1 kHz,信号时间为1 s,信噪比SNR为5。表3给出了EMD-SG方法和小波方法、文中方法以及其他3种方法的降噪性能指标值。由表3可见,对于含噪声调制信号降噪,文中方法明显优于EMD-SG方法和小波方法。说明文中方法可适用于更多信号的降噪,适应性广。
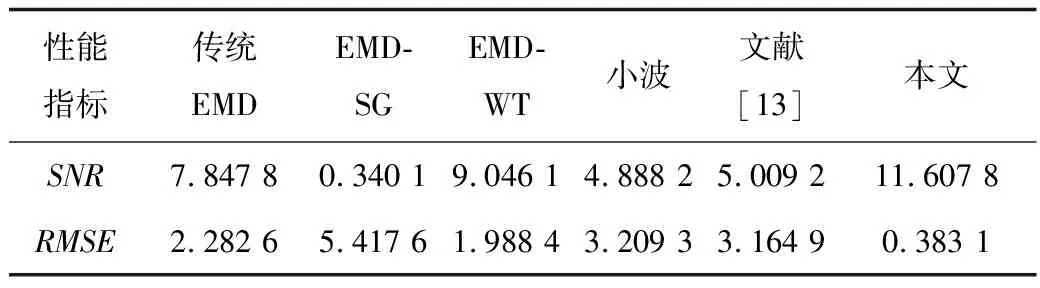
表3 调制信号降噪效果Tab.3 De-noising effect of modulated signals
4 结束语
提出一种基于小波自适应阈值的VMD降噪方法。该方法结合了小波自适应阈值技术和VMD分解技术,能对多类信号进行有效的降噪。通过对多频信号、Doppler信号、多成分信号和调制信号进行降噪数值实验表明:该方法对非平稳降噪具有良好的降噪效果,且适应性广。。

