模块化APF并联建模及谐振分析*

林成，马覃峰，俞秋阳，孙斌，付俊波，王勇

(1.贵州电网有限责任公司，贵阳 550002； 2.南京南瑞继保电气有限公司， 南京 211102；3.上海交通大学，上海 200240)

0 引 言

有源电力滤波器是一种受电网阻抗影响较小且具有优秀动态电流跟踪能力的新型电力电子装置，能够对负载电流中幅值、相位、含量等动态变化的谐波进行跟踪补偿[1]。如果给定的电流指令是系统的无功或者不平衡分量，利用相同的电路结构还能对系统无功和不平衡进行补偿。相对于传统的LC调谐滤波器，有源电力滤波器的动态跟踪能力更好，能够灵活应用于各种负载条件下的谐波治理，虽然其单位补偿能力成本较高，结构、控制也相对复杂，但是随着电力电子技术的不断发展和人们对谐波治理的标准越来越高，有源电力滤波器将成为日益完善的谐波治理方案。

并联型有源电力滤波器作为一个受控电流源，通过在连接点注入与负载谐波电流大小相等、相位相反的补偿电流来治理电网中的谐波[2-3]。相比于两电平拓扑的APF，三电平APF具有直流电压高，输出电流纹波小，硬件结构紧凑，等优势，具有更广阔的应用前景。模块化设计是APF研究领域的一项重要课题，模块化设计的APF具有更宽的控制带宽和更快的谐波跟踪能力，但是与组串式的光伏并网逆变器类似，APF的模块化并联也会遇到LCL滤波器耦合，线路阻抗变化，系统谐振等问题[4-6]。文献[6-8]提到了，并联系统的谐振与电网阻抗、滤波器参数的密切相关。

首先建立了单台APF小信号等效模型，从PCC处将单台APF等效模型拓展到多台并联模型，通过对谐振电流特性的分析，我们得出了两台APF并联具有与N台APF并联相似的谐振电流特性，分析了APF补偿电流突变和并联台数对并联系统谐振特性的影响。最后，通过实验研究，验证多台APF并联系统小信号等效模型和谐振特性分析的正确性。

1 多台并联APF数学模型

1.1 模块化APF的基本结构

如图1所示，每台APF通过LCL滤波器与公共连接点(PCC,Point of Common Coupling)连接。L1，L2，C1，Lg分别表示APF侧电感，网侧电感，滤波器电容和电网阻抗。

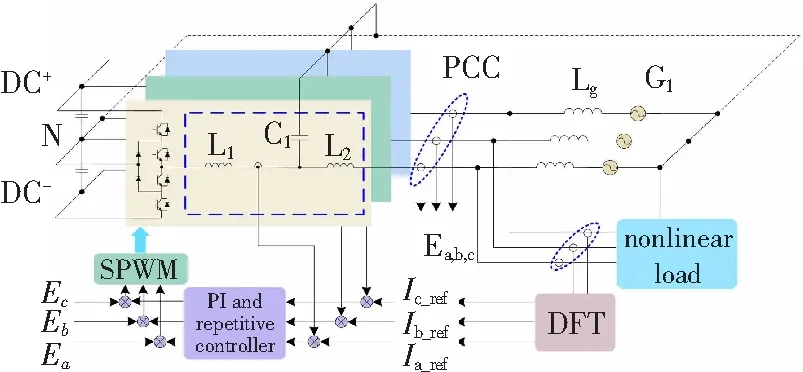
图1 模块化APF的基本结构Fig.1 General structure of modular three-level APF

为了建立并联系统的等效模型，首先建立单台APF的小信号模型。单台APF的控制框图如图2所示。所采用的输出电流控制策略是A-B-C坐标系下的直接电流控制。电压外环叠加于电流内环之上，通过PI和重复控制并联的控制器进行输出电流反馈跟踪。此外，还在电流内环上叠加了一个用于控制上下电容电压均衡的均压环。电压外环和均压环的时间常数均大于电流内环。由于电压外环和均压环都是叠加在电流环之上的，而且并联系统的谐振也往往是由于输出电流引起，故下文主要讨论APF的电流环。

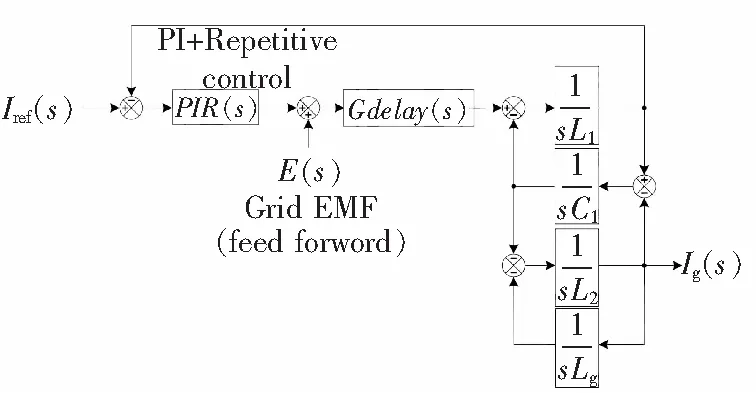
图2 控制器框图Fig.2 Control block diagram of APF

根据图2控制器的框图，可以得到输出电流Ig(s)的传递函数：

(1)

其中：

H1(s)=PIR(s)Gdelay(s)

(2)

H2(s)=s2L1C1+sC1PIR(s)Gdelay(s)-Gdelay(s)+1

(3)

H3(s)=s2C1(L2+Lg)PIR(s)Gdelay(s)+s(L1+L2+Lg)-sLgGdelay(s)+PIR(s)Gdelay(s)+s3L1C1(L2+Lg)

(4)

式中Ig(s)、Iref(s)和E(s)表示输出电流、指令电流和电网电压前馈;PIR(s)是控制器的传递函数；Gdelay(s)表示系统采样、计算和传输的延时。

1.2 单台APF小信号等效模型

APF实质上是一个具有输出电流反馈控制的受控电流源[9-10]。图3是所提出的单台APF等效模型。它包含两部分：三电平逆变器(带LCL滤波器)和电网。三电平逆变器部分包括指令电流Iref(s)和ZI(s)。ZI(s)表示反馈控制引入的并联输出阻抗。电网由电网电压E(s)和电网阻抗ZE(s)组成。ZE(s)包括了由电网电压前馈引入的阻抗。

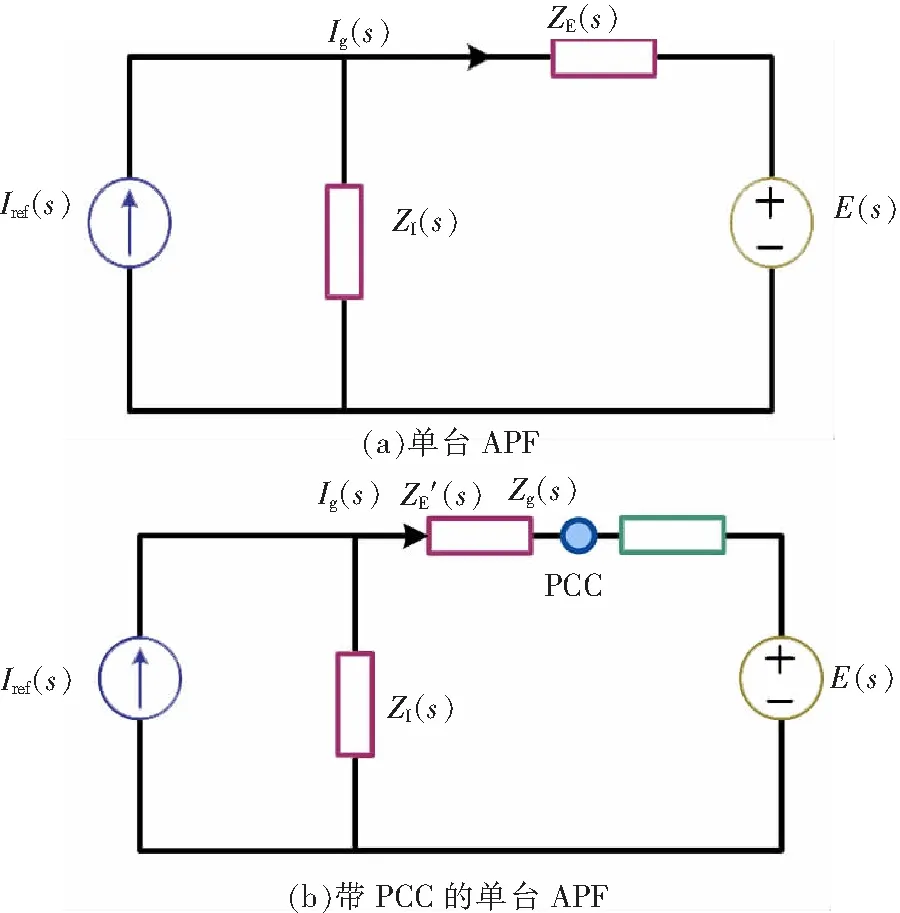
图3 两种等效模型Fig.3 Two kinds of models

基于等效模型和叠加原理，单台APF的输出电流表达式为：

Ig(s)=[ZI(s)Iref(s)]/[ZI(s)+ZE(s)]+

E(s)/[ZI(s)+ZE(s)]

(5)

联立式(1)和式(5)，可以得到：

ZI(s)=[-PIR(s)Gdelay(s)]/[s2L1C1+

sC1PIR(s)Gdelay(s)-Gdelay(s)+1]

(6)

ZE(s)=[s3L1C1(L2+Lg)+s(Lg-Gdelay(s))+

s(L1+L2)+s2C1(L2+Lg)PIR(s)Gdelay(s)]/

[-s2L1C1-sC1PIR(s)Gdelay(s)+Gdelay(s)-1]

(7)

1.3 并联APF系统小信号等效模型

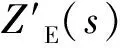
s3L1C1L2+s(L1+L2)]/[-s2L1C1-sC1PIR(s)Gdelay(s)+

Gdelay(s)-1]

(8)

(9)

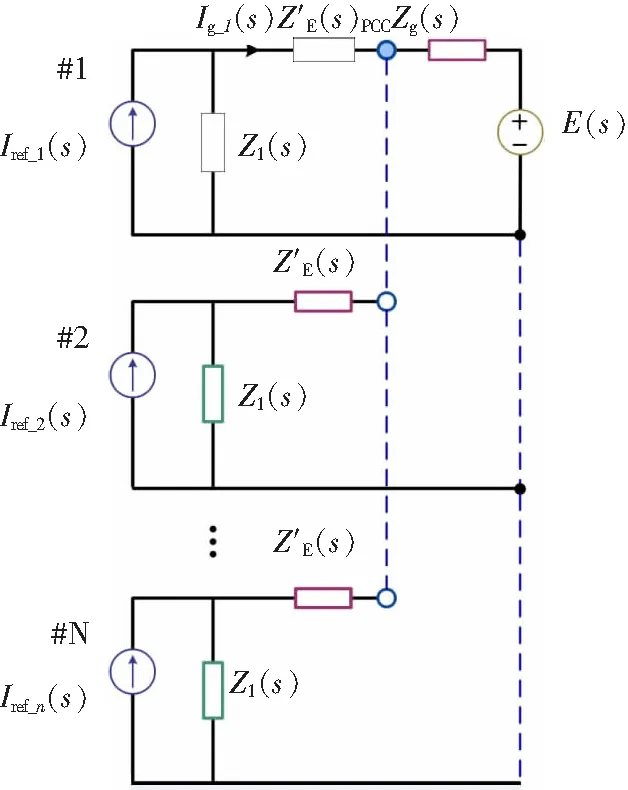
图4 并联APF的等效模型Fig.4 Model of the paralleled APF system

由于并联APF的LCL参数和控制器相同，所以各台APF的输出阻抗可以认为相同。以#1 APF为例，根据基尔霍夫电流定律和线性电路叠加定理[11]，我们可以得到并联等效模型中#1 APF的输出电流表达式：

(10)

其中N是并联APF的台数。式(10)由三个部分组成，表示#1 APF的输出电流含有三个激励源。这三个激励源分别记为#1 APF的指令电流Iref_1；并联系统中其他APF的指令电流Iref_n和电网电压E(s)。GP(s)，GN(s)和GE(s)分别表示输出电流Iref_1(s)相对三个激励源的传递函数。

为了得到三个传递函数的表达式，首先定义图5中的两个阻抗ZP1和ZP2。ZP1表示仅由Iref_1激励时，其余N-1台APF和电网的等效阻抗。ZP2表示当激励源是其余并联APF的指令电流时的N-2台APF和电网的并联阻抗。

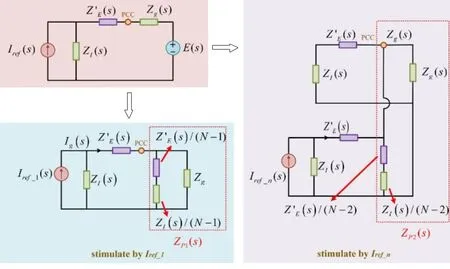
图5 Iref_1和Iref_n激励时的等效模型Fig.5 Equivalent model of Iref_1 and Iref_nstimulated by two different sources

(11)

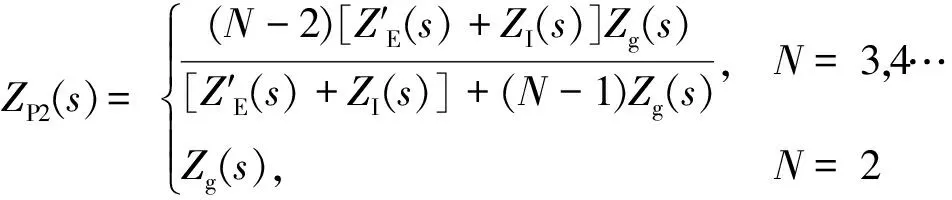
(12)

由以上等效电路可以得到GP(s)，GN(s)和GE(s)的表达式：

(13)

(14)

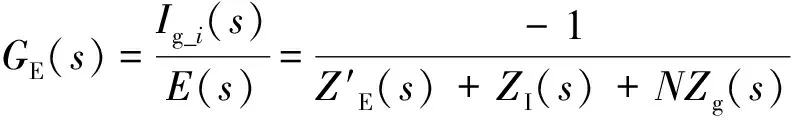
(15)

则并联APF系统的输出电流有以下的矩阵表达式：

(16)

2 模块化并联系统的谐振分析

2.1 谐振电流的特性

为了分析并联系统APF之间的耦合和系统谐振电流的特性，本节建立了并联APF的简化模型。

当考虑两台APF的并联耦合时，其与多台APF并联系统的区别主要在于当并联系统的台数不一样时，输出电流的表达式(10)不一样，表现在GP(s)，GN(s)和GE(s)的表达式含有N。

对于任意的传递函数G(s)，设其表达式为：

(17)

记运算符Porder[G(s)]为取传递函数的分母分子阶数差，即Porder[G(s)]=b-a。

根据上文定义的运算符，当并联APF台数N=j且j大于2时，有：

(18)

(19)

这表明GP(s)和GN(s)的分母分子阶数差没有随并联APF台数的增加而改变，则有：

Porder[GN(s)|N=j] =Porder[GN(s)|N=2]

(20)

Porder[GP(s)|N=j]=Porder[GP(s)|N=2]

(21)

由于上述传递函数的极点均在s平面的左半平面或原点，且分母分子阶数相同，所以其具有相似的自由运动的模态和权重，也即两台APF并联具有与N台APF并联相似的特性[9,12]。

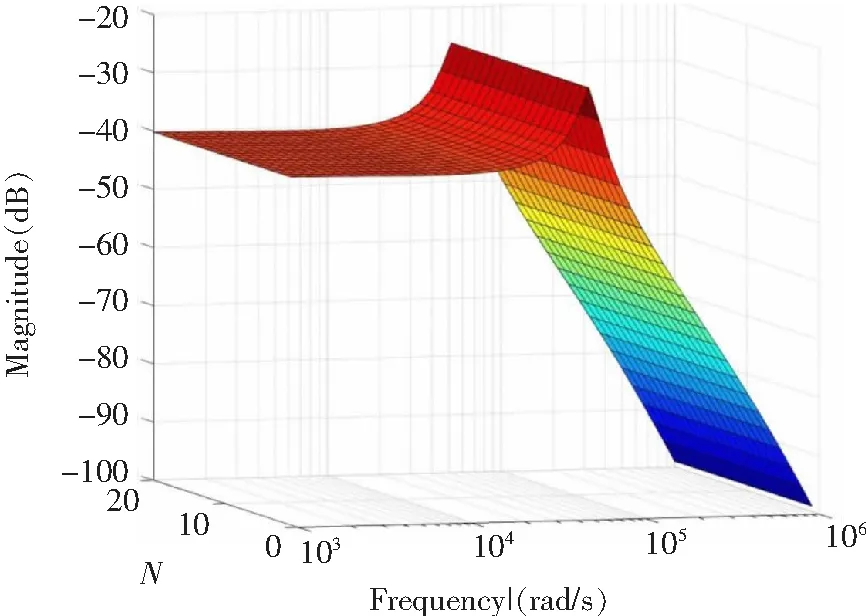
图6 并联台数变化时GP(s)的波特图Fig.6 Bode diagram of GP(s)with different N

仅考虑第一台APF的输出电流时，并联系统的简化等效模型如图7所示，由于此时不考虑其余APF的激励，可以将他们等效为一系列的并联阻抗，考虑到上文所讨论的两台耦合与多台APF耦合的相似性，下文以两台APF并联为例，分析并联系统谐振电流的特性。根据简化等效模型可以得到此时的系统传递函数如图8所示。

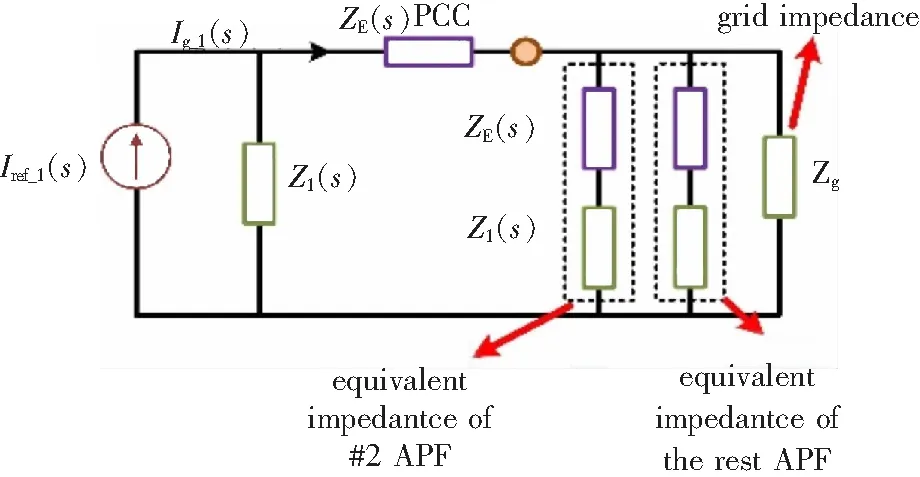
图7 用于谐振分析的并联系统简化等效模型Fig.7 Simplified model of parallel SAPF used for system resonance analysis

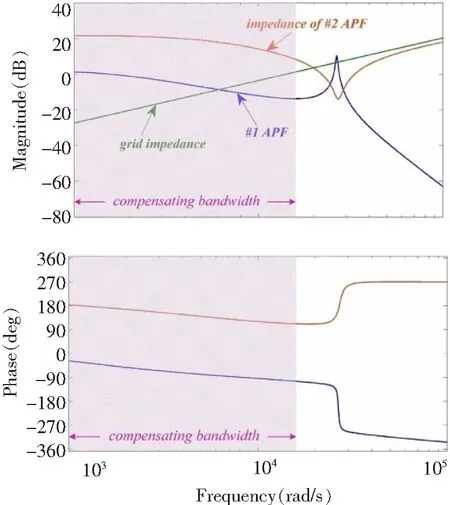
图8 并联系统简化等效模型的波特图Fig.8 Bode diagram of parallel SAPF used for system resonance analysis

从图8可知，#1 APF的输出电流由#2 APF的并联阻抗和电网阻抗分流，从图中可以看出，在频率低于10 000 rad/s的范围内，电网阻抗小于#2 APF的阻抗，所以APF的输出电流主要流向电网。在谐振点处，#2 APF的阻抗急剧减小，小于电网阻抗，这意味着谐振电流将流入#2APF，而不是流入电网，也就是说，并联系统的谐振电流将在APF之间流通，而不会流入电网。因此，只要能抑制单台APF的谐振，就能抑制并联系统的谐振。

3.2 并联系统的谐振

在实际应用中，随着APF输出电流的增大，LCL滤波器的感值会发生衰减，所使用的电感实测衰减曲线如图9所示。从图中可知，电感的感量随着输出电流的增大而减小，当滤波器感值减小一半时，系统的高频衰减特性变差并且相位裕量显著减小，容易发生谐振。

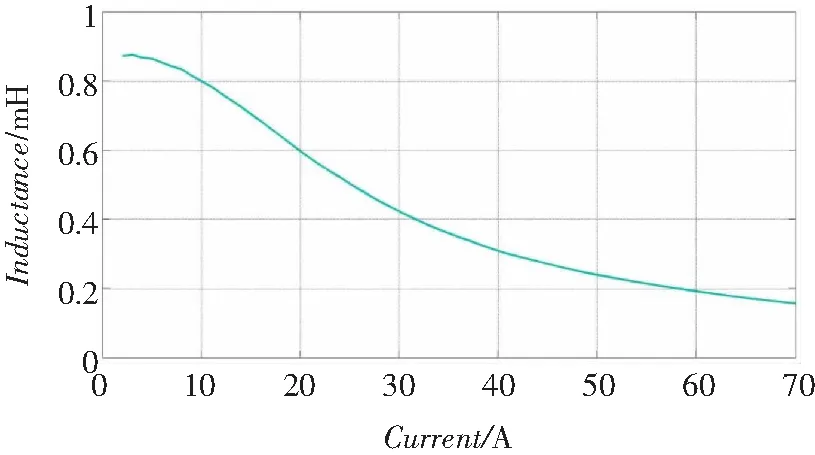
图9 LCL 滤波器电感的衰减曲线Fig.9 Magnetic biasing of LCL filter inductor

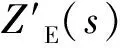
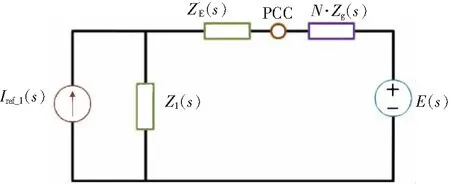
图10 并联系统的单台等效模型Fig.10 Single equivalent modeling of parallel system

根据并联系统的单台等效模型可以画出此时的系统波特图，如图11所示。从图中可知，当并联台数增加时，单台等效模型中的电网阻抗增大，因此，系统的谐振峰左移。与基波逆变器不同，APF需要输出高频的谐波电流，例如150 Hz到5 000 Hz，因此APF的输出电流需要较大的带宽。但是随着并联台数的增加，谐振峰左移并且系统相位裕量减小，从而容易发生谐振。

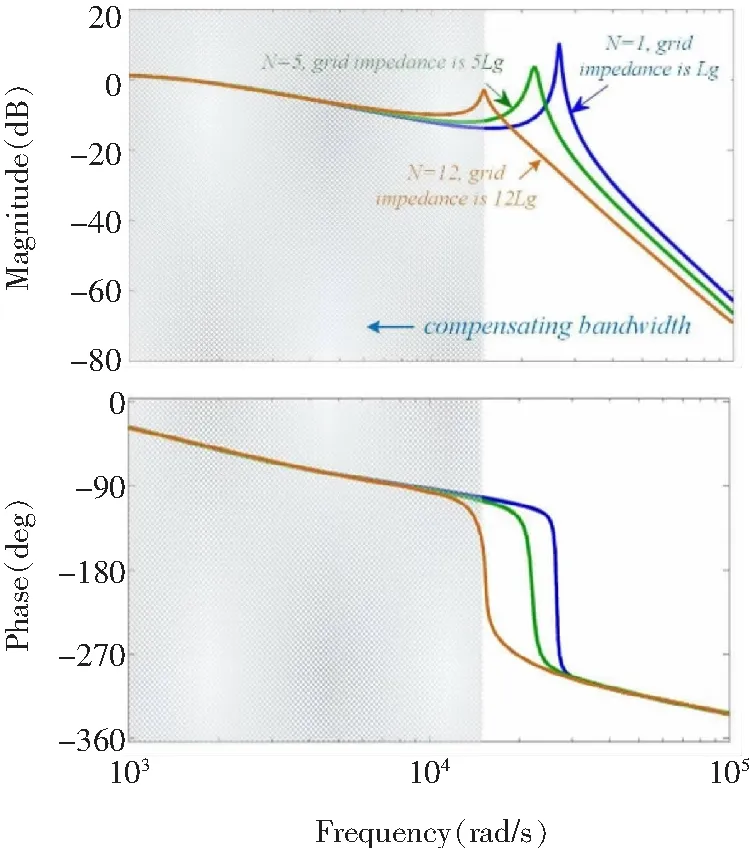
图11 电网阻抗增大时的单台等效模型波特图Fig.11 Bode diagram of single APF with grid im pedance increase

4 实验验证

为了验证分析，在三台额定容量为100 A的三相四线制有源电力滤波器上进行了实验验证，负载为三相不控整流桥，表1是样机的相关参数，图12为样机实物照片。

表1 样机参数表Tab.1 Prototype parameters

图12 样机实物图Fig.12 Prototype figure

图13为负载电流突变实验验证结果，通道1为三相不控整流桥负载电流波形，通道2和3分别为#1和#2 APF输出的补偿电流波形。在t=0 ms到t=48 ms之间，#1和#2 APF并联稳定运行，在t=48 ms时，负载电流增加两倍，并联系统输出电流谐振。在从实验结果可知，由于负载电流突增，从而APF输出补偿电流增大，导致LCL滤波电感感量减少，引起输出电流谐振现象。

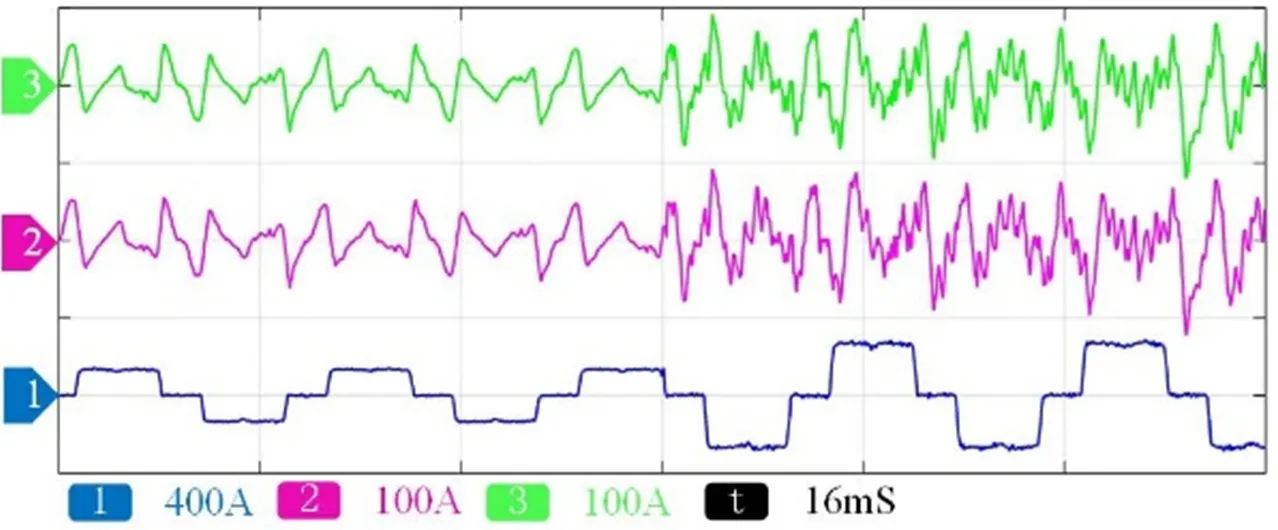
图13 负载电流突变实验波形Fig.13 Test results when the load current changes

图14为APF并联台数变化实验验证结果，通道1-3分别为#1、#2和#3 APF输出的补偿电流波形。在t=0 ms到t=48 ms之间，#1和#2 APF并联稳定运行，输出电流无谐振现象，在t=48 ms时，#3 APF启动，并联系统输出电流谐振。在从实验结果可知，由于并联台数增加，电网等效阻抗增加，APF输出补偿电流增大，谐振峰左移并且系统相位裕量减小，从而发生谐振。

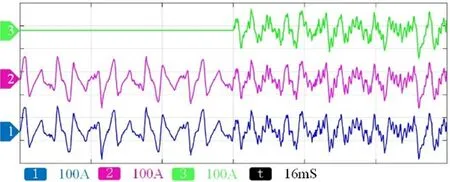
图14 并联台数变化实验波形Fig.14 Test waveform with the parallel number changes

5 结束语

建立了单台APF小信号等效模型，并且将单台APF等效模型拓展到多台并联模型，通过对谐振电流特性的分析，我们得出了两台APF并联具有与N台APF并联相似的谐振电流特性，分析了APF补偿电流突变和并联台数对并联系统谐振特性的影响。实验结果表明多台APF并联系统建模和谐振特性分析的正确性。