基于差分进化算法的船舶能量管理系统优化策略
杨泽鑫,肖健梅,王锡淮,邓军
上海海事大学物流工程学院,上海201306
0 引 言
全球船舶市场的激烈竞争导致行业内需要性能更好的船舶能量管理系统来降低船舶运行成本[1]。而船舶大型化和船舶数量的不断增加,则使得海上温室气体排放量不断上升。近年来,温室效应不断加剧,造成了一系列严重后果。这使得世界各国对环境保护越来越重视,船舶的节能减排和可持续发展问题受到广泛关注[2]。因此,在优化船舶能量管理系统时,既要考虑运行经济性,又要考虑环保性[3-4]。
针对这一问题,已有不少学者进行了研究。Michalopoulos等[5]研究了含有轴带发电机的能量管理策略,结果表明,轴带发电机的使用可以降低船舶动力系统的运行成本和温室气体排放量。Shang等[6]提出了一种将发电调度、负荷管理(推进力负载—巡航速度)和储能系统(ESS)调度相结合的全电力船舶能量管理系统,采用非支配排序遗传算法(NSGA-II)对柴油发电机组的运行进行优化,大量仿真结果证明了该方法的经济性和环保性。Chen等[7]通过研究基于负载功率传输模型的能量管理策略,提出了使得电站波动最小的性能指标,并采用粒子群算法(Particle Swarm Optimization,PSO)寻优,完成了系统电站和储能元件之间的能量分配。Tsekouras等[8]提出了一种含有可再生能源和储能系统的能量管理策略,并从经济性角度对含有光伏发电和储能系统的船舶电力系统的边际成本进行了分析。但以上学者均是对新型船舶电力系统进行研究,忽略了广泛应用的经典船舶能量管理系统的优化问题。
本文将运用差分进化算法(Differential Evolu⁃tion,DE)研究经典船舶能量管理系统的优化问题。拟以某客渡船为研究对象,在总负载、电力服务负载、推进力和船舶航速等预测数据已知的情况下,考虑发电机和柴油机的燃油消耗率(FC)曲线、电力系统运行限制以及温室气体排放量约束,运用差分进化算法、粒子群算法、遗传算法(Ge⁃netic Algorithm,GA)优化调度策略,对船舶航速、发电机组启停状态、发电机组功率分配进行优化调度,通过多种方案的比较,证明差分进化算法对本问题的有效性。
1 船舶能量管理系统的数学模型
1.1 目标函数
船舶能量管理系统的优化问题是在满足系统运行约束的条件下对船舶航速、发电机组启停状态、发电机组功率分配进行优化调度。
其目标函数为
式中:C为系统总运行成本;Ce为电力服务系统的总运行成本;Cpr为推进系统的总运行成本。运行成本的计量单位为货币单位(monetary unit,m.u.)。
对于电力服务系统,其总运行成本Ce按式(2)计算。
式中:T为总运行时间;NE为发电机数量;Pij为第i台发电机在时间间隔ΔTj内产生的功率;Fci为发电机的燃料单价;为发电机特定燃料消耗;WCij为每个运行单位的维护成本;QCij为启动成本;tij为系数,对于第i台发电机,若其运行,则tij取值为1,否则为0。
在经典能量管理系统中,由第i台发电机产生的功率Pij为
式中:E为所有运行的发电机数量;Pel-L,j为在ΔTj内由所有运行的发电机提供的电力负载;Pn,i为第i台发电机的额定功率。
任何发电机每小时的燃料消耗(FC)与其产生的功率Pi都可以近似地由二阶或三阶多项式表示:
为了确定系统的最佳工作点,经常使用特定的燃料消耗(SFC)这一参数,它被定义为每小时产生千瓦特功率时的燃料消耗,如式(5)所示。
对于推进系统,其总运行成本Cpr按式(6)计算。
式中:Npr为柴油机数量;Pqj为第q台柴油机在时间间隔ΔTj内产生的功率;Fcq为第q台柴油机的燃料成本;SFCq为柴油机特定燃料消耗,与式(5)类似;WCqj和QCqj分别为每个运行单元的维护成本与启动成本;tqj为系数,对于第q台柴油机,若其运行,则tqj取值为1,否则为0。
在经典能量管理系统中,第q台柴油机产生的功率Pqj为
式中:Y为所有运行的柴油机数量;Ppr-L,j为由所有运行的柴油机提供的推进力负载;Pn,q为第q台柴油机的额定功率。
1.2 约束条件
1.2.1 发电机的相关约束
1)发电机运行约束。
式中,Pmax,i和Pmin,i分别为第i台发电机发出功率的上、下限。
2)发电机组发出的总功率和电力负载之间的平衡。
3)发电机组爬坡速度约束。
式中,Rci为第i台发电机的最大爬坡斜率。
4)发电机组的最小连续运行时间约束。
式中,下标on和off分别代表启动和停机。
5)发电机组最小停机时间约束。
6)预防异常熄火限制(即使最大的发电机离线,发电机也要能够提供足够的负载)。
1.2.2 柴油机的相关约束
1)柴油机运行约束。
式中,Pmax,q和Pmin,q分别为第q台柴油机发出功率的上、下限。
2)柴油机组发出的总功率和推进力负载之间的平衡。
3)柴油机组爬坡速度约束。
式中,Rcq为第q台柴油机的最大爬坡斜率。
4)柴油机组的最小连续运行时间约束。
5)柴油机组最小停机时间约束。
1.2.3 船舶航速和柴油机功率需求的约束
在船舶推进系统的优化方案中,船舶航速可以适当调整以最大限度地减小FC。负责移动船舶的有效推进力Pe-pr与船舶在特定情况下的总阻力(与船舶的货物重量和环境温度等因素有关)和船舶航速V有关,如式(19)所示[9]。
船舶在航行过程中,对航速存在一定的限制:
式中,Vmax,j和Vmin,j分别为相应速度的上、下限。
1.2.4 航行距离的约束
1)船舶初始航行距离和到达目的地时的航行距离约束。
假定船舶在0时刻出发,T时刻到达终点,则
式中:NT为从开始时刻到最后时刻T的离散时间点的数量;Dj为在时刻j的船舶位置;dtotal为航线总行程。
2)船舶到达中间港口时的航行距离约束。
式中:ζ为对应于中间港口的时间间隔集合;dj为在任意时刻j的行驶距离。
根据临界转速计算结果,该变频电动机的机座长度比常规H630-4电动机有所缩短,由2 770 mm缩短到2 650 mm。根据变频电动机频繁变速运行的特点,机座壁也比常规电动机厚,钢板由32 mm加厚到45 mm。
典型的船舶航速、航行距离及其约束曲线如图1所示。
1.2.5 温室气体排放量约束
船舶能效营运指数(Energy Efficiency Opera⁃tional Indicator,EEOI)体现了单位货物周转量(船舶货物量乘以运输量)的温室气体排放量[4],该指标侧重于对船上操作效率的评估,船舶在航行过程中必须遵循EEOI对气体排放的约束[10]。
在时间间隔ΔTj内,ηEEOI定义为每单位运输工作产生的二氧化碳质量的比。
由于温室气体排放与FC成正比,所以其质量可以通过将发电机和柴油机消耗的燃料量分别乘以转换系数ci,cq来计算。因此,船舶在每个时间段ΔTj内的总二氧化碳排放量为
αLF取决于船舶的类型。如果船舶标准乘客人数和车辆数分别为np和nv,实际乘客人数和车辆数分别为n′p和n′v,则αLF为
式中,GT为船舶总吨位。
当船舶处于泊位时,由于船速为0,所以ηEEOI不用式(24)计算,将其修正为[11]
根据各种船舶的设计,常见的环境限制为:
文献[11]提出了多种方法来减少船舶的二氧化碳排放量,并针对船舶的航行重点采取了降低航速的策略,达到了减少温室气体排放量的目的,具有实际参考意义。
1.3 发电调度说明
为了确定发电机和柴油机的使用数量,达到负载功率分配的最优化,需要准确预测船舶负载。这是通过在航行过程中系统地记录货物负载和乘客人数来实现的。除柴油机外,工程空间的辅助系统、生活空间和货舱的空调,特别是游轮的照明等都增加了船舶负载。当给定电力负载的时间顺序曲线,即可选择运行的发电机及其产生的功率。在常规船舶电力系统配置中,通过调整航速来管理负载,减少CO2排放以满足环境约束。在任何情况下,对于实际负载超出预期的小范围波动情况,可以由船舶电力系统使用实时最优控制系统通过适当的发电调整[10]和负载优先启停来管理[12]。
2 差分进化算法
差分进化算法是一种基于种群的智能优化算法,该算法不依赖问题的特征信息,借助于种群个体间的差分信息对个体形成扰动来搜索整个个体空间,并利用贪婪竞争机制进行优化,以寻求问题的最优解。该算法采用实数编码方式,主要解决连续领域的优化问题[13]。该算法的变异方式可以有效利用群体的分布特性提高算法的搜索能力。
对于优化问题:
2.1 差分进化算法流程
差分进化算法是基于实数编码,首先要在问题的可行解空间生成随机初始化种群:xi=(xi,1,xi,2,⋅⋅⋅,xi,D),其中i=1,2,⋅⋅⋅,NP,NP为种群规模。初始种群在参数空间中随机产生,并应覆盖整个参数空间。
在进化的每一代中,对每一目标个体进行变异和交叉操作以产生试验个体,然后对目标个体和试验个体进行选择操作,以选择适应值更优的个体进入下一代。
种群内个体的差分向量经过缩放后,与种群内另外的相异个体相加得到变异向量。
式中:g为代数;r1≠r2≠r3,随机取自于种群集{i=1,2,⋅⋅⋅,NP},这也使得种群的规模NP不能小于4;F为缩放因子,控制差分向量的缩放以避免搜索的停滞,其选择范围为 0.5~1[14]。
在变异之后的交叉过程中,通过随机选择,使产生的试验向量至少有一个分量是由变异向量提供。
式中:j=1,2,⋅⋅⋅,D;jrand为[1,D]内随机选择的整数;CR∈(0,1),为交叉率。
经变异与交叉操作后生成的试验向量ui,g和目标向量xi,g进行竞争。当ui,g的适应度值较优时,其被选为子代;否则,xi,g为子代。
式中,xi,g+1为下一代的目标向量。
2.2 差分进化算法在本文中的实现步骤
以3.1节的方案2为例,运用差分进化算法对电功率分布进行优化。其实现步骤如下:
步骤1:根据给出的初始数据,在可行解空间随机生成规模为NP的初始化种群(包含机器运行状态、速度、发电机和柴油机输出功率),设置最大迭代次数G,令g=1。
步骤2:对初始化种群中的数值进行修改,使之满足约束条件(发出功率上下限约束、开/关时间约束、EEOI约束等)。
步骤3:判断是否满足终止条件,若是则退出,否则执行下一步。
步骤4:对每一个体xi,g执行步骤5~步骤8,生成g+1代种群。
步骤5:在种群中随机选择3个不同的个体,按式(30)进行变异操作,生成变异个体vi,g并按步骤2进行调整。
步骤6:按式(31)进行交叉操作,生成试验个体ui,g,并按步骤2进行调整。
步骤7:按式(32)进行选择操作,生成g+1代目标向量xi,g+1。
步骤8:g=g+1,返回到步骤3。
3 仿真与分析
3.1 仿真方案的提出
为了验证差分进化算法对本问题的有效性,采用文献[5]中的数据进行对比验证。该文中客渡船的总吨位为48 750 t,其最高航速为23.5 kn,最大运输量为1 800名乘客和500辆汽车,EEOI1的最大允许CO2排放值为21 g/(t·kn),EEOI2的最大允许CO2排放值为120 g/(t·h)。使用差分进化算法、粒子群算法和遗传算法对船舶能量管理系统进行优化,并将其结果与文献[5]的优化结果进行对比。
仿真运行的船舶配置有3台发电机和2台柴油机,每台柴油机都通过轴连接一个螺旋桨推进装置。发电机和柴油机的所有必要技术参数见表1。
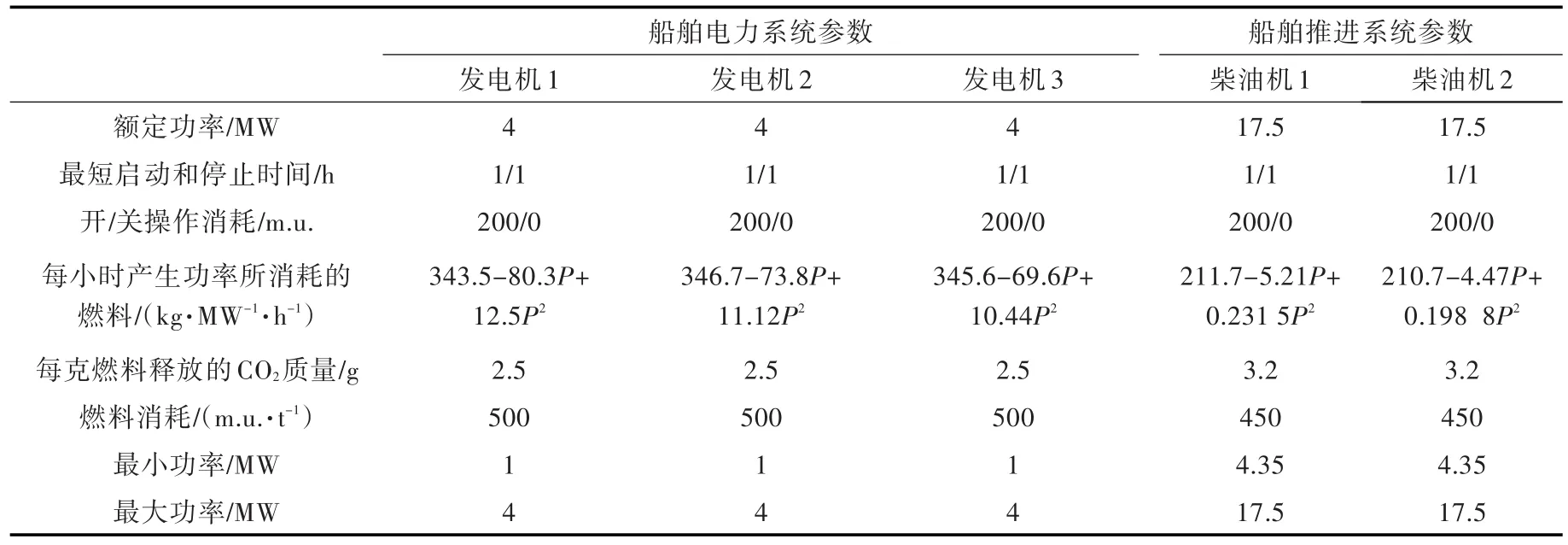
表1 船舶动力系统模型数据Table 1 Ship power system model data
这里模拟一条总里程为307.744 2 n mile的航线。航线中有3个中间港口,经港路线各部分的乘客、车辆和相应的船舶负载因数如表2所示。该次航行的船舶初始推进力和速度规划曲线、总负载和电力服务负载预测曲线如图2所示。
发电机根据运行优先级编号,它们连续的启动和停止之间的最小允许时间为1 h。每台工作的柴油机都会以相同的推进负载驱动螺旋桨,柴油机也按照其运行优先顺序编号。
本文采取3种不同的运行方案,具体操作如下:
方案1:配有3台发电机和2台独立的推进柴油机,不采用最佳功率调度、推进调整,无EEOI限制,发电机和柴油机采用比例分配方法。

表2 船舶满载度数据Table 2 Data for ship fullness
方案2:配有3台发电机和2台独立的推进柴油机,采用最佳功率调度,有EEOI限制,不采用推进调整。
方案3:配有3台发电机和2台独立的推进柴油机,采用最佳功率调度、最佳推进调整,有EEOI限制。
3.2 仿真结果与分析
方案1的运行成本为36 960.5 m.u.,方案2的运行成本为36 938.1 m.u.,方案3的运行成本为35 888.3 m.u.。方案2和方案3的运行成本随进化代数变化的曲线如图3所示。由图中可以发现,差分进化算法(DE)与粒子群算法(PSO)和遗传算法(GA)相比,对本问题有更好的稳定性和收敛性。
在方案2和方案3中提出的能效管理方法用于推导最优电功率分布和最优推进调整,以最大限度地提高船舶电力系统的运行效率,并限制整个行程中的EEOI。所得结果如图4~图8所示。假设在所有运行工况下,柴油机1、发电机1和发电机2在t=1时已经运行0.5 h。
由主发电机和推进系统柴油机产生的功率如图4所示,将其总功率与总需求负载(电力需求加上推进负载需求)进行比较。图中,EG为发电机,PM为柴油机。
在方案1~方案3中,推进力负载被平均分配给运行的柴油机;方案1中,电力负荷也被平均分配给运行的发电机,在方案2和方案3中,分配方式有变化。发电机1连续运行,发电机2几乎连续运行(时间段T13~T17除外),而发电机3则仅在高电力负载期(T26~T28)运行。
在方案1和方案2中,船舶航速和推进力未调整,只对电功率分布进行调整,所以其结果仅在电功率分配中不同。船舶总负载在相邻时间段会发生较大偏差,不能保持相对稳定,运营成本降低量可以忽略不计。
在方案3中,进行电功率和推进力的最佳调整。方案3中的最佳电力调度与方案2的情况非常相似,但柴油机的发出功率有很大改变,船舶总负载在相邻时间段波动较小,运营成本有很大的降低。
方案1~方案3中船舶每个时间间隔的航行速度如图5所示。方案3与方案1和方案2相比,随着推进力得到最佳调整,在海上航行时,船舶航速保持相对稳定;当接近港口时,船舶航速降低,到达港口时速度降为0;当从港口离开时,船舶航速增加。通过这种方式,船速和推进力负载曲线变得相对稳定,不会过于离散,如图6所示。这使得船舶运行成本的曲线更加接近梯形,操作更经济,如图7所示。此外,船舶航速虽然偏离了初始(非优化)的预定值,但不会超过其上限(23.5 kn)。在中间港和目的港,航行距离的限制也是满足的。
EEOI在所有时间间隔的值如图8所示。方案3采用推进调整和EEOI限制,能够保证在其上限(海上航行时为21 g/(t·kn)和泊位时为120 g/(t·h))之下。方案2和方案1相比虽然不能满足此限制,但方案2的EEOI值略小于方案1。
如前所述,方案1和方案2不包括推进调整,而方案3包含,由图5~图8可知,船舶速度变化和预期的一样,方案1和方案2中的船速保持不变,方案3中观察到速度的变化,这是因为提供推进力的柴油机功率进行了调整以满足EEOI限制。
方案1的总运行成本为36 960.5 m.u.,如果采用最优电力调度方案2,则总运行成本降至36 938.1 m.u.(减少0.06%),温室气体排放量也略有下降。如果在经典船舶配置中实施推进调整(方案3),则总运行成本降为35 888.3 m.u.(减少2.90%),并且完全满足EEOI限制。
因此,仿真结果表明,本文提出的优化方法有效降低了运行成本,减少了温室气体的排放。
3.3 与已有文献结果的对比
对比本文方法与采用动态规划算法的文献[5]可以发现,在相同的仿真条件下,文献[5]中的方案2与方案1相比运行成本减少了0.05%,而本文方法则减少了0.06%。同样,文献[5]中的方案3与方案1相比运行成本减少了2.02%,而本文方法则减少了2.90%。结果表明,采用差分进化算法对船舶能量管理系统进行优化调度,能够在满足各种同等船舶运行约束的条件下,使运行消耗更小,满足EEOI限制,且船舶航速更平稳。
4 结 语
本文针对船舶电力系统运行成本最小化的需求,提出了一种将差分进化算法应用到船舶动力系统的最优功效管理方法。仿真结果证实了差分进化算法的有效性,尽管同时考虑经济性和环保性会使问题变得复杂,但还是能够在满足船舶电力系统的技术和运营限制(包括生产和消耗平衡、总航行距离、温室气体排放等限制)的同时,实现运行成本最小化。所提出的算法可用于评估任何船型,它是完全参数化的,不依赖于船舶柴油机或发电机的任何特定特征,因为它的主要输入是发动机和发电机的燃油消耗率曲线。

