基于BP神经网络的船舶主机能效状态评估
陈伟南,黄连忠,张勇,路通
大连海事大学轮机工程学院,辽宁大连116026
0 引 言
对船舶主机而言,其能效状态由主机的设定转速、外界的海洋气象状况、船舶载重、船舶姿态等多个因素共同决定。在传统的船舶管理模式中,船舶操纵人员大多依靠自身经验对主机状态进行评估,并依据评估结果进行操作。这种评估具有极大的不确定性,并降低了船舶的能源利用效率[1]。
刘伯运等[2]和孙宜权等[3]针对车用柴油机的状态评估进行了分析。在船用柴油机方面,周根明等[4]运用层次分析法对船舶主机的整体健康状态建立了评估体系;孙峰等[5]基于数据挖掘技术提出了一种评估船用柴油机性能的方法。这些方法虽然对船舶主机的能效状态评估进行了研究,但并不能对航行中的船舶主机状态进行实时、迅速的评估。叶睿等[6]利用神经网络构建了客滚船的主机油耗模型,但其输入参数较为复杂,没有进行简化处理,同时其输入参数仅为船舶航行时的船体姿态数据,并未包含主机的运行参数,这也影响了模型的可靠度与准确性。
基于此,本文将以状态良好的船舶运行记录作为样本,结合主成分分析法和反向传播(Back-Propagation,BP)神经网络智能算法,构建船舶航行状态识别模型和主机油耗模型。在构建油耗模型时,将利用主成分分析法对模型输入参数进行简化,从而降低数据噪声和网络复杂性。此外,本文油耗模型的输入参数还将包含主机的运行参数和船舶的航行姿态参数,用以更准确地反映主机的能效状态。本文构建的航行状态识别模型可用于识别船舶当前的航行状态,而油耗模型可用于判断船舶主机当前的能耗状态是否正常,从而对主机能效进行智能、准确的评估,可为智能船舶的能效评估研究提供一定的参考。
1 构建模型
采用船舶的航行状态模型和主机油耗模型对主机状态进行评估的流程如图1所示。首先,采集船舶的实时运行数据,将其输入到基于神经网络构建的主机航行状态识别模型中,运用该模型识别出主机不同运行数据对应的航行状态;然后,选取正常航行状态数据,运用主成分分析法对数据进行预处理,用以降低后续计算的复杂度,加快神经网络的收敛速度并减小误差;接着,将处理后的航行状态数据输入到基于神经网络构建的主机油耗模型中,得出主机的功率、转速、油耗等参数;最后,将主机的实际油耗值x2与理论油耗值x1进行实时对比,得到油耗残差值δ,即可判断主机当前的运行状态是否正常。
1.1 目标船及数据
本文的船舶实时运行数据均来源于某目标船——30万吨级远洋矿砂运输船。该船总长327 m,型宽55 m,型深29 m,设计吃水21 m,航速14.5 kn,载重 298 000 t,主机型号为 MAN B&W 6S80MC-C,额定功率为22 360 kW,额定转速为73 r/min。
通过船载传感器进行数据采集工作,目标船的状态参数如表1所示。其中,风速分解为沿船舶航行方向(X方向)和垂直于航行方向(Y方向)2个风速,并分别以船艏来风和右舷来风为正。

表1 目标船状态参数Table 1 State parameters of target ship
传感器每隔30 s采集一次数据,为保证模型的稳定性,以5 min时长为间隔来处理所采集的数据。其中,除主机油耗量数据为5 min内的累计值之外,其他数据均为5 min内的均值。
X方向和Y方向的风速分别为
式中:N为5 min内传感器采集的总次数;Vwc为风速仪第c次采集的相对风速,其中c=1,2,…,N;θc为船舶航向与风向之间的夹角。
主机缸套水的进口、出口温差平均值ΔT为
式中:Tin为主机缸套水的进口温度;Toutg为1~6号气缸缸套水的出口温度,其中g=1,2,…,6。
1~6号气缸排气温度的平均值Tˉ为
式中,Tg为1~6号气缸的排气温度。
1.2 BP神经网络
对于输入参数繁多的船舶航行状态识别模型和油耗模型而言,若构建一般的函数,则难以准确描述各物理量之间的因果关系,且普通函数对各型船舶的通用性较差[6]。本文将采用BP神经网络来构建模型。BP神经网络是一种非线性智能算法,具有运算速度快、容错能力高、自学能力强等特点,是目前应用最广泛的神经网络模型之一。BP神经网络可以学习和存储大量的输入—输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程[7-9]。
BP神经网络是一种多层前馈型神经网络,其拓扑结构如图2所示。图中:P1,P2,…,Pn为BP神经网络的输入参数;b1,b2,…,bm和θ1,θ2,…,θk为网络的偏置;a1,a2,…,ak为网络的预测值;ωij和ωjh为BP神经网络的权值。其中i=1,2,…,n;j=1,2,…,m;h=1,2,…,k。
图2中的网络包括n个输入节点和k个输出节点,表达了从n个自变量到k个因变量的函数映射关系。网络中隐含层第j个节点的输出结果yj和输出层第h个节点的输出结果ah分别为
式中,f1和f2分别为输入关系和输出关系的传递函数。
本文将采用Matlab软件来构建神经网络,选取f1为双曲线正切函数tansig,f2为线性变换函数purelin。BP神经网络的学习分为2个阶段:第1个阶段是根据输入的已知样本,从第1层向后计算各神经元的输出;第2个阶段是从最后一层向前计算各权值和阈值对总误差的影响,进而修改各权值和阈值。这2个阶段反复交替进行,直至函数收敛。为了提高网络的收敛速度,本文选用列文伯格—马夸尔特(Levenberg-Marquardt,LM)算法作为第2个阶段的计算方法,并以均方误差函数作为性能函数。
1.3 主成分分析法
航行状态识别模型的输出结果分为5种,即停泊、机动航行、正常航行、冲车航行和大风浪航行,其设计输入为相对风速Xˉ和Yˉ、船舶航速Vs、主机转速ne、主机曲轴扭矩M、主机曲轴功率Pe及主机燃油消耗量F,运用BP神经网络算法可以实现较高准确度的航行状态识别。
然而,对于主机油耗模型而言,其输出结果是具体的燃油消耗量,其输入参数多达10项(表1中前10项)。在此情况下,变量之间有一定的关联性,故变量提供给BP神经网络的信息会存在重叠,从而增加了计算的复杂性,减缓了网络的收敛速度,降低了模型的准确性并提高了BP神经网络过拟合的可能性[10-11]。如果神经网络过于复杂,会使信号和噪声同时进行拟合,从而导致神经网络的预测值与实际值严重不符,而采用大量的数据对网络进行训练并降低训练数据的噪声则是避免出现过拟合问题的有效方法[12]。因此,本文除了采用大量数据对模型进行训练之外,还将应用主成分分析法(Principal Component Analysis)对油耗模型的输入数据进行预处理以降低数据噪声。
主成分分析法的实质是在不改变样本数据结构的情况下,通过旋转多维空间的坐标将原变量转换成两两不相关的主成分,同时尽可能反映原变量所包含的信息,从而简化计算[13-14]。本文将采用主成分分析法与BP神经网络算法相结合的方法,假设样本矩阵X为
式中:样本矩阵X中第v个参数类型中的第u个样本数据为xuv,其中u=1,2,…,n且v=1,2,…,p;xu=[xu1xu2…xup]T,为p维列向量。
样本矩阵的均值xˉ为
协方差矩阵S的表达式为
对于n行p列的样本矩阵X而言,经过矩阵变换后即得到样本协方差矩阵S,其为p行p列的方阵,故式(8)之后的u=1,2,…,p且v=1,2,…,p。
协方差矩阵S中的任一元素Suv为
式中:xu′u和xu′v分别为样本矩阵X中的某个元素,其中u′=1,2,…,p;
设Suv的p个特征值分别为且其单位正交特征向量tˆ为
则第u个样本的主成分yu为
2 航行状态识别模型
对正常航行的船舶而言,在实时评估其主机能耗状态之前,应先识别当前船舶的航行状态。在停泊状态下,船舶航速、主机转速、耗油量基本为0;在机动航行状态下,各项参数基本在停泊状态和正常航行状态的数值特征范围内波动;在正常航行状态下,各项参数基本稳定在一定范围内;在冲车航行状态下,各项参数将出现波动且有所增加;在大风浪航行状态下,相对风速将明显增加,而船舶航速将有所降低。根据不同航行状态的参数特征,将现有的历史数据进行统计分类,即可得到各个航行状态的样本数据。
为了实现较高准确度的航行状态识别,本文将以船舶航速、相对风速、主机转速、曲轴扭矩、曲轴功率和主机油耗量作为输入,船舶航行状态作为输出。同时,还需要设定神经网络计算矩阵的目标值,即停泊为[1 0 0 0 0]T、机动航行为[0 1 0 0 0]T、正常航行为[0 0 1 0 0]T、冲车航行为[0 0 0 1 0]T、大风浪航行为[0 0 0 0 1]T,然后进行训练学习。在Matlab软件中建立并训练BP神经网络时,设定训练函数为trainlm、学习函数为learngdm、性能函数为mse、隐含层和输出层的传递函数分别为tansig和purelin,其中2层隐含层的神经元数量均为10。训练函数trainlm采用LM算法,该方法结合了梯度下降法和牛顿法的优点,可以有效避免陷入局部最优解并保证收敛速度[15]。
本文将选取目标船在新加坡—圣路易斯航段(2015年03月20日至2015年04月06日)作为训练样本,即该时间段内船舶和主机均处于良好状态下的航行数据,其中停泊记录22条、机动航行记录33条、正常航行记录153条、冲车航行记录14条、大风浪航行记录114条。
为了验证模型的准确性,本文选择了4个月后的航行记录模型作为检验样本,即目标船在马迹山—新加坡航段(2015年07月19日至2015年07月22日)内连续77 h的样本数据,仿真结果如图3所示。图中,各分图的横坐标均为传感器数据采集点的序号。
图3(g)所示的评估航行状态图即模型识别所得的船舶航行状态,图3(h)所示的实际航行状态图即通过查询该目标船轮机日志和航海日志后统计得出的船舶实际航行状态,其纵坐标数值1,2,3,4,5分别代表停泊、机动航行、正常航行、冲车航行、大风浪航行这5个状态。由图3可知,在第0~120采集点之间,船舶航速、主机转速、扭矩、功率、油耗等均为0,识别模型判断为停泊状态,判断准确;在第120~135采集点之间,船舶和主机的各项参数均出现了波动,模型将其识别为机动航行状态,判断准确;在第128点左右,由于船舶的短暂提速,模型将其识别为正常航行状态,判断错误;在第135~486点之间,模型判断船舶为正常航行状态,经查询航海日志,该目标船确实为正常航行状态,判断准确;在第486~719点之间,风速提高、船速降低,模型判断为大风浪航行状态,经查询航海日志,判断准确;在第885~892点之间,各项参数均出现了波动且有所增加,模型判断为冲车航行状态,经查询轮机日志,该目标船在此时间段确实进行了冲车操作,故模型判断准确。由此可知,模型判断整个样本的识别正确率为98.05%,从而为下一步建立主机油耗模型提供了基础。
3 主机油耗模型
3.1 主成分分析处理
应用BP神经网络构建主机油耗模型时,需要先对训练样本进行主成分分析。本文选取了目标船在2015年3~5月的船舶和主机运行数据作为训练样本,该时间段内目标船和主机均处于良好运行状态。选取表1的前10个参数作为主成分分析的原始变量,设定主成分Z1~Z10,计算所得的成分矩阵如表2所示,各主成分对应的特征值、方差贡献率及累计方差贡献率如表3所示。
由表3可知,Z1~Z5的累计贡献率为93.87%,而Z6~Z10的贡献率则很小。因此,本文将选择Z1~Z5作为表述样本内容的主要数据来计算各项主成分的系数,结果如表4所示。根据各主成分的系数,将原训练样本的10种原始变量转换为5项主成分,即可作为BP神经网络的输入数据。
3.2 建立油耗模型
在matlab中设定BP网络油耗模型的训练函数为trainlm、学习函数为learngdm、性能函数为mse、隐含层和输出层的传递函数分别为tansig和purelin。对于隐含层的层数和神经元节点数目,目前缺乏设定最优数目的明确指导方法,本文将设定神经元节点数目的取值范围为0~20,然后采用循环程序遍历2层隐含层中所有神经元数目组合的模型训练误差,最后根据计算所得的训练误差值确定最优的神经元数目设定。如图4所示,将3.1节中已处理的主成分数据信息作为BP网络的设计输入,通过循环程序即可得到不同神经元数目组合的训练误差结果。

表2 成分矩阵Table 2 Component matrix

表3 总方差解释Table 3 Total variance interpretation
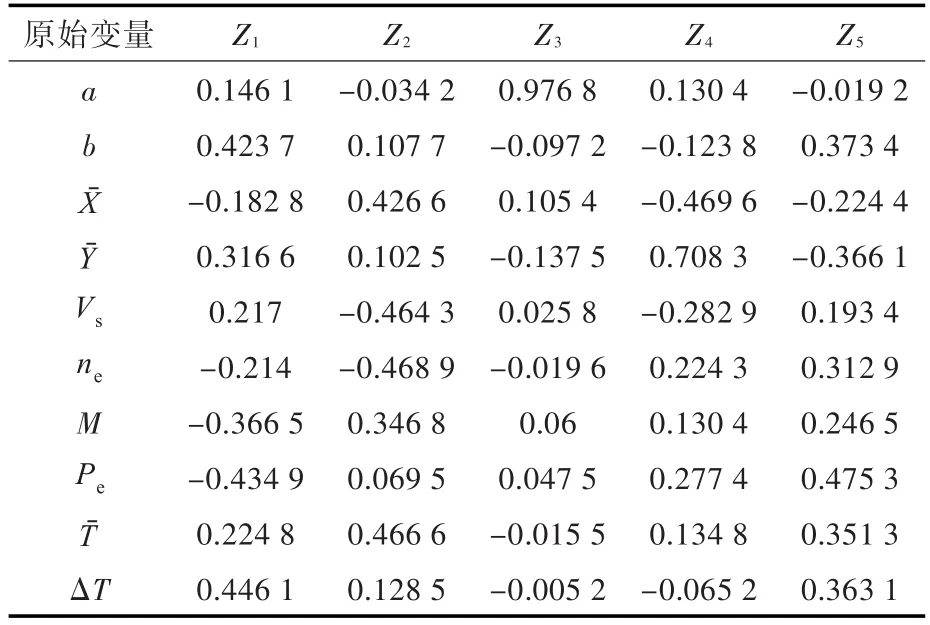
表4 各项主成分的系数Table 4 The coefficients of each principal component
经计算,当第1层隐含层神经元数目为16且第2层为11时,数据整体的均方误差最小,其值为6.325 9×10-5。因此,本文设定BP神经网络中2层隐含层的神经元数目分别为16和11,然后,即可建立并训练网络,最终得出正常航行状态下的主机油耗模型。
需要指出的是,由于不同的船舶和主机的匹配关系与性能均有所差别,所以针对其他船舶构建航行状态识别模型和主机油耗模型时,还需要重新通过计算机程序进行神经网络训练,所需的时间成本也应在可接受范围内。本文已经确定了神经网络训练的模式和函数,故可以推广应用至其他船舶和主机。
3.3 模型验证与分析
选取目标船在圣路易斯—马迹山—新加坡航段(2015年05月19日至2015年05月24日)的部分航程作为验证样本,经航行状态识别模型提取正常航行状态数据,并根据各主成分系数计算得出5项主成分参数,输入BP神经网络即可得出对应的理论油耗值,结果如图5所示。
由于主机燃油流量计数器的输出数据精度为0.01 m3,故图5中的实际油耗值曲线存在幅值为0.01左右的波动,但总体趋势与计算油耗值曲线一致。在第150个数据点附近,计算油耗值出现了小幅降低,船舶的曲轴扭矩和功率分别在1 620 kN·m和9 600 kW左右波动,略低于整体平均水平1 673 kN·m和10 022 kW,而实际油耗值也出现了降低现象,可见计算结果与实际运行情况相符。在第500个数据点附近,实际油耗值出现了异常高峰点,经查为传感器的暂时故障所致,而其他数据点的传感器工作正常。由图5可知,主机油耗模型的总体平均相对误差为3.47%,且未产生明显的过拟合现象。
将实际油耗值和计算油耗值进行对比,以残差形式体现主机的能效状态,如图6所示。
由图6可知,在该段航程内的各项工况下,主机的性能特征与良好能效状态相吻合,即主机能效状态正常。同时,由于主机燃油流量计数器的输出数据精度为0.01 m3,故大部分样本数据点的耗油量残差都在-0.01~0.01范围内波动。
4 结 语
本文结合实船航行数据,运用BP神经网络算法建立了船舶航行状态识别模型,可以有效识别船舶的5种航行状态,其准确率达98.05%。同时,依据船舶和主机的10个运行参数与主机燃油消耗量之间的关系,采用主成分分析法降低了各个变量之间的关联性和复杂性,并运用BP神经网络算法构建了船舶主机正常值油耗模型,其总体平均相对误差为3.47%。通过综合运用这2种模型,可以对正常航行状态下的主机实时状态进行评估,可为智能船舶的能效管理提供参考。

