纵向减振推力轴承液压减振系统的热平衡性能分析

陈繁 ，李天匀 ，赵耀 ，朱翔

1华中科技大学船舶与海洋工程学院，湖北武汉430074

2高新船舶与深海开发装备协同创新中心，上海200240

3船舶与海洋水动力湖北省重点实验室，湖北武汉430074

0 引 言

液压减振系统广泛应用于车辆、船舶及航空航天领域，相比于弹簧和橡胶减振器，其优势在于对低频段的振动可提供较大的阻尼，对高频段的振动可提供较大的动刚度。

本文研究的对象为纵向减振推力轴承液压减振系统。由于螺旋桨在不均匀伴流场中运转时会使轴系产生纵向振动，故在推力轴承内安装了液压减振器［1］，以吸收轴承振动并减少突变载荷对船体带来的影响。然而，若轴系振动时间过长，而液压系统吸收的能量不能快速得到散失，会造成液压系统局部的温度升高（以下称“温升”），从而对船体构件产生不利影响。因此，需要预报液压减振系统的产热和散热性能，以便采取相应的温度控制措施。

目前，计算液压系统的产热主要有如下方法：按元器件计算法、按系统输入功率和执行元件输出功率的整体计算法、实验法［2］及有限元法［3］等。按元器件计算法的基本思路是分别计算系统的具体产热部位，如管道接口、活塞和溢流阀等部位。牛宏杰等［4］在对滑移装载机液压系统的热平衡研究中分别对泵、发动机及管路损失进行了计算。郭洪江［5］和王剑鹏等［6］在研究装载机液压系统的热平衡时也分别用到了局部产热计算方法，但这种计算需要知道各构件的特定参数（如工作效率、油路压差），且计算时构件的散热效率也要根据经验值获取。因此，此方法一般适用于油路较为简单或尺寸较为规则的液压系统，且需要知道液压系统构件的某些特定参数，以能够较全面地呈现出结构的具体产热分布情况。

此外，按系统输入功率和执行元件输出功率的整体计算法能比较准确地计算系统整体的能量损失，其基本思路是将系统视为热交换载体，系统总输入功率与执行元件总输出功率间的差值即为系统总产热功率。邓永建［7］在已知泵和发动机总效率的基础上对汽车起重机液压系统的总体产热进行了预报。这种从整体能量角度考虑系统产热方法的优势在于计算思路清晰，分析过程也较为简单，但仅能大体评估系统产热的等级，适用于具有完整回路的液压系统。这类系统的油箱内部一般设置有冷却系统，液压油流经油箱冷却后再次经泵流入回路［8］，其散热分析较为简单。

然而，上述解析方法计算的油路均为较常见的结构，对于一些复杂壁面结构则无法查取散热系数的经验值，故仍需用到热分析有限元法（如AMESim［7，9-10］，ANSYS，FLUENT［11］，ABAQUS［12］，CFD［13］等）或实验法。邓永建等［7，9-10］利用 AMESim软件建立了液压系统的热特性模型，并与实验结果进行了对比，以验证计算结果的可靠性。前述按元器件计算法、整体计算法和有限元法大多适用于稳态热平衡分析，而对于瞬态产热问题，神经网络分析法［14］和经验公式法［15］则应用得较为普遍。

鉴于文献中的研究对象基本上都具备完整的液压回路，其依靠液压泵提供的动压力来维持活塞的工作。本文将研究的活塞液压减振器为封闭油路，内部流体做往复运动，外部激励力属于不可调控的未知载荷，无法直接运用整体方法估计系统产热，故采用按元器件计算法对各部分产热功率进行计算，即以内部液压油的往复流动以及活塞与壁面相互运动的能量损耗过程为研究对象，分析结构局部的产热，并对特定活塞行程的工况进行产热计算。同时，计算达到满行程时的激励力所做的功，然后与总的能量耗散进行对比，以验证方法的准确性。两者的计算以相同行程的活塞周期振动为出发点，前者的功率输入转化为后者的能量耗散。在分析结构的温升计算时，由于模型形状较为复杂，对于复杂壁面结构无法查取散热系数的经验值，难以利用解析法计算系统的温升，故采用热分析有限元软件对系统进行温升计算，所施加的相应热载荷数值源于对应工况下系统相应部位液动损失及摩擦损失的计算值。

1 系统产热分析

图1所示为一种新型活塞液压减振轴承的结构示意图［16］。图中：部件1为支撑架，部件2为柱塞，部件3为止推块，部件4为前推力块，部件5为推力环，部件6为后推力块，部件7为球面支座，部件8为壳体，部件9为活塞液压腔。在轴系旋转过程中，推力环5和前推力块4间形成楔形动压润滑膜，以传递螺旋桨静推力。前推力块4背面设计有止推块3，止推块3与柱塞2接触，可起到将推进轴系纵向振动传递至共振转换器内液压油的作用。

活塞液压系统产热主要有2个来源：一是活塞往复振动时与缸壁间的摩擦损失；二是液压油流经输油管道产生的液动损失［17］。本文所有产热计算的结果均以功率来量化表征。

1.1 活塞与缸壁间的摩擦损失

分析该摩擦损失时，需要确定活塞与缸壁的间隙。根据国家标准GB 1800-79［18］，本文选取的活塞基本公差等级为g，对应选取H8为基准孔的公差代号，g7为活塞的公差代号，即液压缸壁的上偏差为+39 μm，下偏差为 0 μm，活塞的上偏差为-9 μm，下偏差为-34 μm，故活塞间隙h=9～73 μm。对于保证高度密性的接合表面（如活塞、柱塞缸等构件表面），粗糙度Ra的值不大于0.05 μm［18］；如 图 2 所 示 ，Ra=0.05 μm 与h=9～71 μm相比，影响几乎可以忽略不计，由此可知，活塞表面非常光滑，可忽略两者间接触点的剪切作用所产生的摩擦力影响，油液的粘性作用构成了活塞与缸壁间的摩擦力［19］。

假设活塞的行程为2H，即活塞在振动过程中的最大轴向位移长度。在外部激励力未知的情况下，假设活塞的振动方程为

式中：x(t)为活塞的轴向振动位移；ω为振动角频率；t为振动时间。

活塞的运动速度u1(t)为

在分析活塞腔和输油管道内部液压油的液动损失，以及活塞壁与活塞腔壁间液压油的摩擦损失时，需研究活塞腔体和输油管道内液压油的运动过程。鉴于油箱体积远大于管道内部液压油的体积且油箱封闭，本文忽略了油箱内部液压油的速度，而对液压油经过输油管流入油箱后的损失则不做研究。此外，液压油的体积模量极大，难以压缩，故忽略液压管道内的液体压缩性，且假设液压油的体积压缩均发生在油箱内。

本文将液压油视为牛顿流体，即在活塞与活塞壁间的流速沿厚度方向呈线性分布。如图3所示，两个表面油膜厚度为h，最大相对流速为则剪应力τl(t)与速度梯度dv1(t)/dh成正比，即

式中：μ为润滑油的动力粘度，则摩擦力

式中，Ar为活塞产生摩擦部分的名义接触面积；D1为活塞缸横截面直径（式（6）中表示为D）；lh为活塞的轴向接触长度；，为摩擦表面的粘性阻尼系数。

此外，若采用O形密封圈，活塞环与缸壁间的摩擦阻力f2还可由下式计算［22］：

式中：η为活塞密封圈与缸壁间的摩擦系数；γ为活塞密封圈材料的泊松比；N为活塞间隙中液压油的压强；d为O形密封圈的圆形截面直径。

因此，对于活塞间隙摩擦产热功率P1，可由下式计算［22］

式中：dx(t) 为式（1）的微分，即dx(t)=Hωcos(ωt) dt；T为周期。

1.2 液压油运动的液动损失

系统内部液压油通过输油管时产生液动损失，压缩后存储为弹性势能以供复原时使用［23］。图4所示为液压系统的简化模型［24］。图中：D2为输油管的横截面直径；u1,u2分别为活塞的运动速度和输油管内液体流速；V1和V3分别为活塞缸与油箱的体积。

对于液压阻尼减振器的力学模型假设如下［24-25］：液压缸为刚性，液压油体积压缩均发生在油箱内，故不考虑输油管及活塞缸体内液压油的体积压缩。活塞腔内液压油体积变化量ΔV1表示为

式中：A1为活塞缸的横截面积；A2为输油管的横截面积。

将式（2）代入式（7），可得

假设流体在管道内以层流流动，根据达西公式［26］，液压油被视为牛顿流体，其在活塞缸与输油管内流动的水头损失hf1和hf2之和为

式中：λ1，λ2分别为活塞缸和输油管内的沿程阻力系数（根据米勒公式，和Re2为雷诺数，对于圆形管道，其中υ为液压油的运动粘度，g为重力加速度）；L1，L2分别为为液压缸储油部分的轴向长度和输油管的长度。

流体在管道内运动消耗的瞬时功率Pr(t)为

式中：ρ为液压油的密度；Q为输油管内体积流量。流体运动消耗的平均功率P2则为

2 外部激励力做功计算

在上节中的液压油液动损失及活塞摩擦损失功率计算中，液压油均被视为不可压缩流体。外部激励力做功则需压缩液压油来实现，即在计算外部激励力做功时，需考虑流体的压缩性。

图5所示为液压阻尼减振器的力学模型［24-25］，可将该系统视为在周期激振力作用下单自由度的质量—弹簧—阻尼系统的受迫振动。模型所受外部激励力F0未知，而行程2H为已知，前述能量损失计算均为活塞满行程的运动，故需先根据模型的振动方程推导出在活塞满行程运动时所需的外部激励力F0，然后再对结构整体的外部激励力输入功率进行计算。其运动方程由下式表示：

式中：M，Mb分别为被隔振物体的质量和基座质量，通常Mb≫M，即F0ejωt为外部激励力；均为式中各参数的表达式，其中B为液压油的体积模量。

整理式（12），得到运动微分方程如下［27］：

其中ω0为振动系统固有频率，由此可求得受迫振动的运动规律，即

式中，θ为相位角，

H与a0的关系如下：

则外部激励力F0为

其平均做功功率P3为

3 算 例

本文参照具体模型计算选取的参数如下［24］：lh=85 mm，D1=48 mm，μ=0.23 Pa·s，H=1.5×10-3m，B=5×108Pa，ρ=890kg/m3，L1=0.76 m，A1=1.8×10-3m2，A2=5×10-5m2，V3=0.007 5 m3，d=4.8×10-4m，γ=0.5，M=1.54×103kg。

计算时，式（5）中的摩擦系数η的选取与液压油压力有关。在带液压油润滑条件下，O形橡胶密封圈可形成润滑水膜。流体压力越高，液压液体（例如，水）越容易渗入接触面，润滑状态也就越好，摩擦系数也越低［28］。取活塞间隙中液压油的压强N=5 MPa，并按文献［20］取O形橡胶密封圈与缸壁间的摩擦系数η=0.05。

若按最大产热值计算，则应取最小的活塞间隙为9 μm。活塞与缸壁间的摩擦产热功率P1计算结果如表1所示。

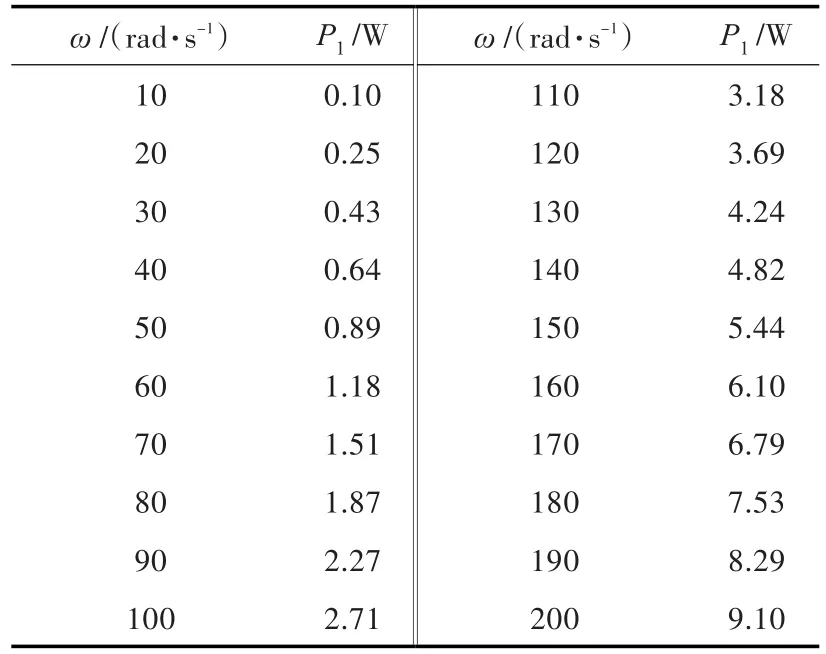
表1 摩擦产热功率随振动角频率的变化Table 1 Variation of the friction heat power with different angular frequencies

对式（11）进行计算，可得到流体运动消耗的平均功率P2随振动角频率ω的变化结果，如表2所示。

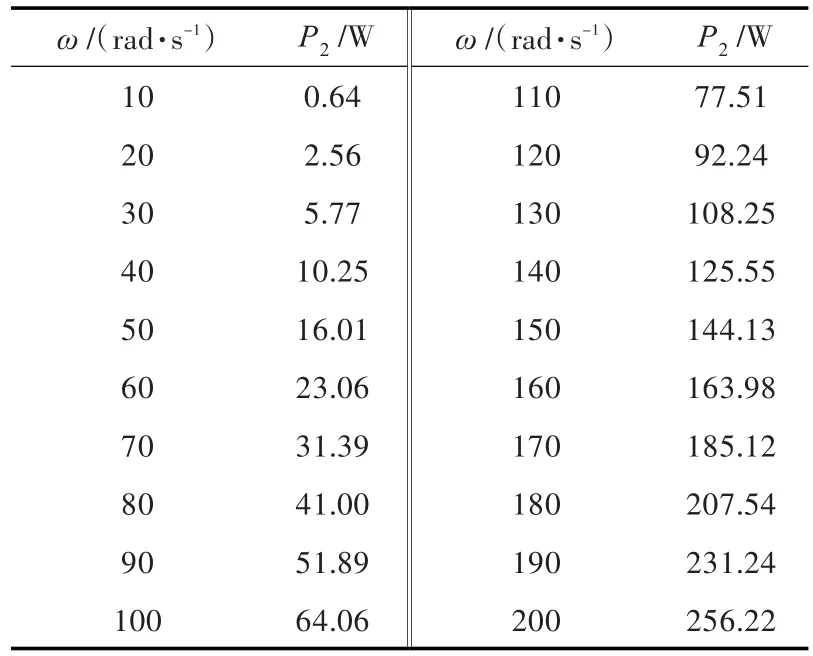
表2 不同振动角频率下液压油液动损失功率Table 2 Head loss of the hydraulic oil with different angular frequencies

将上述计算所得到2种功率损失随振动角频率ω的变化情况进行对比，如图6所示。

综合上述结果，按照如下计算公式计算得到活塞与活塞壁间摩擦产热的总产热占比κ，结果如表3所示。

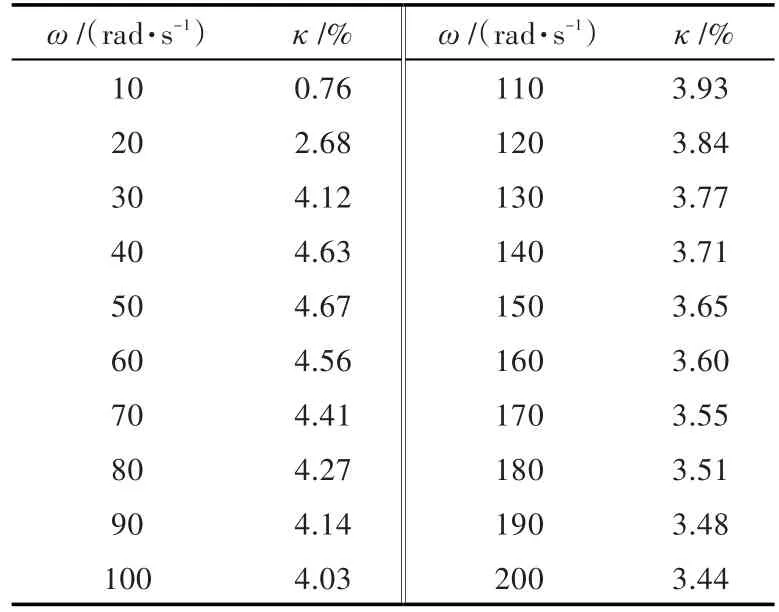
表3 摩擦产热功率占比Table 3 Percentage of the friction heat power

由表3可知，不同振动角频率下活塞的摩擦散热占总散热的比率均低于5%，即活塞摩擦损耗占总能量损失的比重较小，活塞内部流动的液压油的液动损失是主要产热来源。

利用式（16）计算外部激励力平均做功功率P3，结果如表4所示。

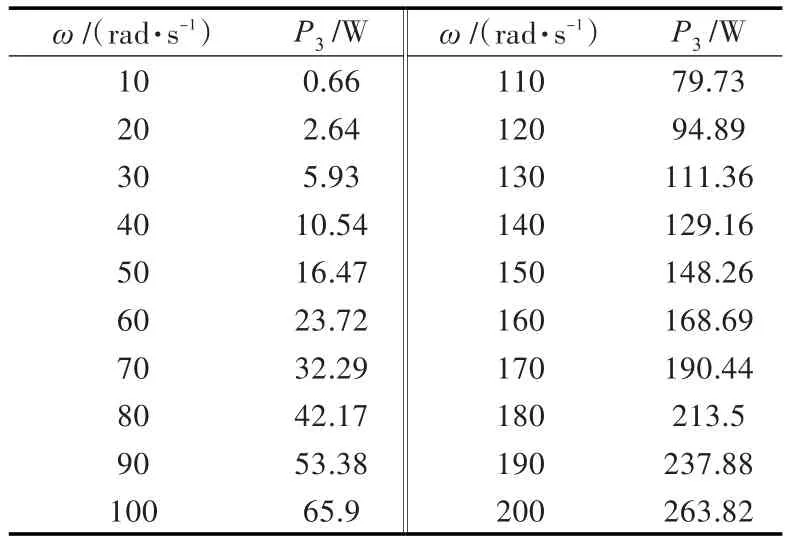
表4 激振力做功功率随不同振动角频率的变化Table 4 Variation of the input power of exciting force with different angular frequencies

将表2和表3中系统的产热功率值与表4中外部激励力输入功率进行比较，如图7所示。图中，外部激励力输入功率曲线系统的产热功率接近于重合，实际上两者的数据存在细微差别。外部输入功率曲线相对于系统总输入功率曲线偏下，这主要是因为式（12）仅考虑了油箱内液体的压缩性，而忽略了输油管道和液压缸内的油液压缩性，此时推导出的活塞满行程运动所需的激励力偏小，所以利用式（16）计算所得的激振力的输入功率相比于分步计算得到的产热值偏小。总体上，两者数据间的差别较小，即外部激励力做功可近似视为活塞运动转换的摩擦损失和液压油流动的液动损失，这也表明忽略管道内液压油的压缩性并不会对激励力输入功率的计算结果造成较大影响。

此外，令行程从1 mm变化到5 mm，计算在不同行程和振动角频率下活塞满行程运动时系统的产热功率，结果如图8所示。

由图8可知，系统产热功率分别随行程和振动角频率的增加而增大。当选取的功率参考值为100 W和H=0～2.5 mm时，若要使系统输入功率控制在100 W以下，则需ω＜50 rad/s。当ω=0～200 rad/s时，若要使系统输入功率在各行程下均低于100 W，则需H＜1 mm。

4 系统温升分析

上述活塞及液压油产生的热量，通过缸体及管道传递到外部，然后分析活塞缸体部位的散热，并计算稳态散热系统的温升。

首先，选取ω=200 rad/s和H=1.5 mm，其他参数与上述模型一致。按照图9，在三维建模软件SolidWorks中建立如图10所示的液压减振系统模型。

然后，将模型导入ANSYS有限元软件中，并按上述模型设置材料属性，取活塞、缸体及轴系的材料属性为钢材。表5给出了钢材及液压油的导热系数、密度和比热容［29］。导入的模型中缸体、活塞及液压油均采用Solid 87实体单元，并进行网格划分（图11）。因活塞尺寸较小，该部位采用细网格，以使计算更加精确；而缸体尺寸较大，采用粗网格，以缩减计算时间。

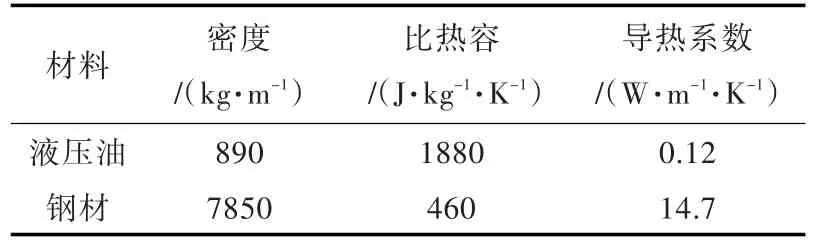
表5 材料属性Table 5 Material property

最后，在ANSYS有限元软件中对模型施加相应的热学载荷。一般情况下，外部空气与缸体表面接触，将缸体与外界接触的表面温度恒定为25℃。由上述产热的计算结果可知，当ω=200 rad/s，H=1.5 m时，流体运动消耗的平均功率P2=256.21 W，活塞间隙摩擦产热功率P1=9.10 W。

假设摩擦产热的热源位于活塞相对运动的壁面上，分析时在活塞相对运动接触面上施加9.10 W的热流载荷，其液动损失发生的部位位于缸壁及管道处，而油路为两端封闭、不循环的双向往复流动，这时液压油热量会再次带入液压缸和油箱内（对于外部油箱中的液压油温升，这里不做研究）。为计算活塞部位的最高温升以及简化温度载荷施加过程，本文在活塞的缸壁面上均匀施加256.21 W的热流均布载荷，即为通过该面的总热功率。图12所示为具体载荷示意图。

由于所有实体部件间按水密性要求的粗糙度进行了配合，各装配件实体间的接触被视为无其他介质的完整面接触，所以忽略各部件间的粗糙度（即介质带来的接触热阻影响）。另外，由于所有实体材料均取相同的材料参数，并将各部件实体单元整体建模，从而省去了复杂表面的接触热阻设置。本文将热流载荷面施加在流体与结构的交界面处，仅设置了通过分界面处的热流功率。

图13所示为减振推力轴承部位静态导热的有限元分析结果，且可将其近似视为活塞部位稳态热传导的计算结果。

由图13（a）可知，液压系统活塞部位的最高温度达到25.11℃。当ω=200 rad/s，H=1.5 mm时，有限元传热学模型数值计算结果表明，温升仅在1℃范围内，此温升结果并不会使液压油的物理性质发生显著改变［8］；此外，得到的最高温升部位位于液压缸壁靠近轴中心的一侧，这是因为内侧热量传递得较为集中，且内部润滑油导热系数相较于缸体的低，故热量传递效率较低。

由图13（b）可知，沿润滑油流动方向的温度梯度较大，即润滑油静止时的温度传递比缸体的慢，从而导致热量聚集。由图13（c）可知，活塞部位的热量容易由中部向外部传导，这是因为中部散热中心部位的散热性能比周围部分的弱，热量无法得到很快的散失，从而造成中部温度高，热量向四周传导。

综上所述，在实际工况中，若要避免液压系统发生局部温升，首先需使缸体和基座具备良好的外表面散热性能，保持中部的润滑油处于流动状态，使活塞部位的热量向中部传导，并针对液压油建立循环冷却系统。

5 结 语

本文对新型活塞推力轴承液压减振系统的结构形式、工作原理、产热及散热进行了较为全面的分析，对具体模型的活塞摩擦产热和液动损失以及外部扰动的输入功率进行了计算。为分析液压系统温升和散热，建立了轴承部位的热学有限元模型，将特定振动角频率和活塞行程下计算得到的产热功率以热流载荷的形式等效施加到有限元模型上，然后计算结构的稳态温升及热梯度分布，并简要提出了降低系统局部温升的可行措施。由图13（b）可知，活塞内部的润滑油传热导热系数较低，若不发生流动则会造成热量堆积。在实际轴系运行时，输油管道内的润滑油处于循环流动状态，从而将所吸收的热量带出，达到冷却的目的。总体上，液压系统在结构表面散热良好的情况下，计算结果显示的系统温升在1℃范围内，此温升的量级几乎不会对液压油的物理性能产生影响，故没有必要为轴承设置冷却系统，而依靠润滑油的自带冷却即可满足散热要求。当然，也可根据船舶的特殊工况，针对轴承纵向液压减振系统进行具体设计，必要时，可在轴承部位安装温升监控装置，实时监控载荷和油温，并形成反馈机制。