城市可持续发展中的止赎房产处置模式研究
郭 颂
(上海财经大学 金融学院,上海 200433)
目前,随着我国住房规模的持续扩张和经济增长的换挡,已出现了诸如“鬼城”“空城”等泡沫化现象,住房货款违约风险成为城市发展中的一个隐患。发达经济体对住房抵押贷款的风险管理方式有以下两种:一种是通过资产证券化手段将贷款包装成证券化产品,如抵押资产支持证券,担保债务凭证等并对外销售,从而将风险转移出去。另一种是购买相关金融产品如信用违约互换等进行风险对冲。但由于我国缺乏相应的创新工具,风险管理方式也仅仅止步于住房抵押覆盖和借款人现状审查。在当前国内大环境下,住房贷款违约一旦发生,由此产生的资金及信用损失将几乎全部由银行和地方政府承担,严重损害了社会的稳定和城市的可持续发展。
一、文献回顾
房地产市场对城市发展的作用毋庸置疑,众多学者从经济理论和统计分析等角度论证了房地产经济的合理增长对城市经济增长具有重要意义,同时指出,过快或过慢都会影响城市发展的稳定增长[1]。泡沫化的过快增长会对城市化进程产生严重的负面效果,而房地产市场失速带来的违约风险同样会造成金融体系的不稳定[2]。
国外学者很早就开始关注影响住房抵押贷款违约的各类因素,随着期权的应用和推广,从期权定价理论的角度对住房抵押贷款进行相应的定价工作也成为了一个主要研究方向。Kau等[3]以及Kau和Keenan[4]在考虑提前偿付和违约风险的基础上分别从固定利率和浮动利率的假设出发,对住房抵押贷款的定价问题做了相应的研究。另外,随着住房抵押贷款证券化产品的普及,也有相当一部分研究讨论了相关证券化产品(如MBS)的定价问题。Schwartz和Torous[5]通过估计借款者每一期提前支付的概率分布函数研究了MBS的定价问题。Stanton[6]给出了借款者关于提前偿付的理性决策模型,并以此为基础对MBS进行定价。
国内学者在这方面的研究还相对较少。唐文进和陈勇[7]利用期权定价的方法给出了住房抵押贷款的定价结果,同时讨论了利率水平、房价水平与贷款的提前偿还和违约可能性的关系。魏成龙和王述评[8]对于国内住房抵押贷款的提前偿付率进行了相应的实证研究。龚潇潇等[9]在考虑住房投资需求的基础上研究了住房抵押贷款的定价问题。
本文基于国内外学者的研究,从期权角度出发,利用我国房地产市场的数据,针对止赎房产处置问题进行的相关研究具有实际意义和广泛的应用空间。
二、模型构建
我们首先构建市场模型,该模型可以用于描述抵押资产以及与抵押资产相关的资产价格行为。假设市场中的无风险收益率为r,同时存在一类抵押资产和两类金融资产。对于这三类资产我们分别做如下假设:
(一)抵押资产
用随机过程{Pt}表示抵押资产价格,并且假设{Pt}服从下面的伊藤过程:
dPt/Pt= μ(Pt,t)dt+σ(Pt,t)dWt
(1)
其中,μ(Pt,t)为漂移率,σ(Pt,t)为波动率,Wt为标准布朗运动。
抵押资产可以是各种类型的资产,如商品房、股票和债券等。
(二)金融资产Ⅰ
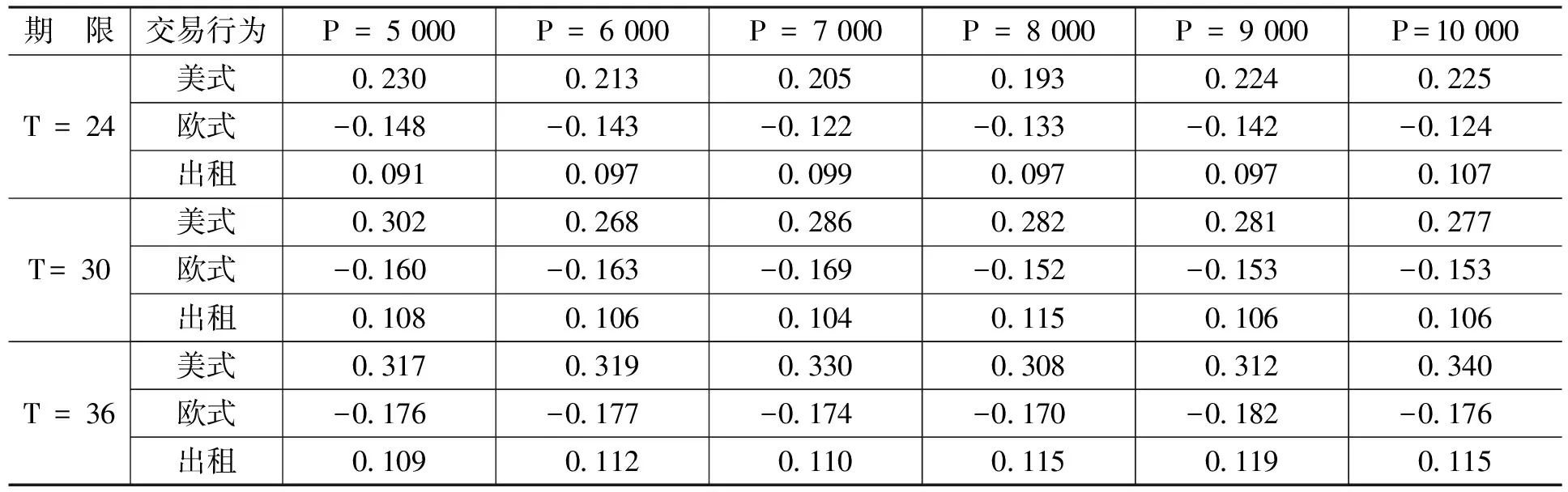
金融资产Ⅰ是关于抵押资产的抵押合同,合约期限为N。合约内容规定,从初始时刻0到合约到期时刻N之间共有n个交易日,即0=t0 金融资产Ⅱ是有条件抵押资产处置合约,合约期限与抵押贷款合同有效期相同。合约规定,当金融资产Ⅰ发生违约的条件满足时,金融资产Ⅱ的合同将开始执行,合同持有者将按照约定的价格购买或者租用抵押资产,其中,买卖或者租用的选择权属于合约对手方(商业银行)。 我们不难发现,金融资产Ⅱ的租用条款实际上是附带租赁服务的以抵押资产为标的的美式看涨期权:租赁期限T为行权期,租赁期内的约定购买价格K=Pt·er(τ-t)为行权价(我们假设以无风险收益率作为连续复利率计算得到的价格为银行可接受的最低行权价),合约对手方为获得权利而缴纳的费用C为期权费。 根据金融资产Ⅰ的理性违约假设,当金融资产Ⅰ发生违约时,有Pt 当然,除执行金融资产Ⅱ的合同外,商业银行也可以选择其他传统的抵押资产处置方式,如直接将抵押资产以违约时的市价Pt在市场中出售变现;或者将抵押资产出租,并且在租期结束后再以当时市价Pt+T对其进行处置的方法等。 相比这些传统方法,金融资产Ⅱ为商业银行处置贷款的抵押资产提供了一种新的选择:利用金融资产Ⅱ,当抵押贷款(金融资产Ⅰ)发生违约时,商业银行可以通过提供抵押资产的租赁服务并收取租金,保持自身的流动性和资本充足率;同时由于银行实际持有抵押资产,因此,在抵押资产价格上涨时,银行也可以从中获得收益。此外,标的资产多头与看涨期权空头组成的抛补看涨期权组合能够降低银行在未来所得收益的波动。 根据传统期权定价理论,在标的资产价格服从几何布朗运动以及其它一些假设条件下,看涨期权的价格C可以由下列偏微分方程给出: ∂C/∂t+(1/2) σ2P2(∂2C/∂P2)+rP(∂C/∂P)-rC=0 (2) 其中,P为标的资产价格,r为无风险收益率,σ为标的资产收益率的波动率。 在欧式期权行权时间确定的约束下(τ=T),我们有初始条件C=max{PT-K,0}·e-rT,进一步地,上述偏微分方程可以得到相应的解析解;而在美式期权结构行权时间不确定的情况下,初始条件C=max{Pτ-K,0}·e-rτ中的停时τ不是一个定值,因而很难得到解析形式的解。另外,在价格路径不服从几何布朗运动的条件下,上述偏微分方程也需要做相应修正。因此,关于美式期权定价问题的研究在绝大多数情况下均是通过数值模拟方法求出其数值解。 假设某美式期权的行权期限为T,除初始时刻外,行权期内有m个交易日(0=t0 (1)找出tm=T时刻(最后一个时点)期权处于实值状态的价格路径,并标记为可能的行权时点(如果处于虚值状态显然不会行权)。 (2)找出tm-1时刻期权处于实值状态的价格路径,并将相应路径上未来时刻(此时为tm时刻)的现金流贴现到当前时点(以美式看涨期权为例,假设第k条价格路径的tm时刻在第(1)步中被标记为行权时点,则贴现现金流为(K-PkT)·e-r(tm-tm-1);否则贴现现金流为0),并将贴现现金流作为被解释变量,将当前时点的标的资产价格和与之相关的其他变量(如价格的平方项、三次方项等)作为解释变量进行回归,得到回归系数的估计。 (3)将选取的解释变量代入回归方程中,得到在当前时点可得信息集的基础上未来贴现现金流的条件期望。 (4)将当前时点立即行权可得的现金流与未来贴现现金流的条件期望进行比较,若当前时点的现金流更大,则记当前时点为新的行权时点,否则不在当前时点行权。 (5)从tm-2时刻起往前的每一个时刻,依次重复上述(2)—(4)的步骤,直到t1时刻为止,得到每条路径可能的行权时点。 (6)将每条路径的期望现金流贴现到初始时刻并取均值,即可得到相应期权的模拟定价结果。 另外,需要特别指出的一点是:通常认为,美式看涨期权在完美的市场条件下不会提前行权,因此其定价结果应该与欧式看涨期权一致。但是针对本文所设计的以抵押资产为标的的美式看涨期权,显然不存在与之对应的流通性较强的二级市场等条件,因此,从数值模拟角度讨论其提前行权的可能性和区别于欧式看涨期权的定价结果仍然具有实际意义。 本文的数据是2000—2016年国内商品房平均销售价格月度数据,单位为元/平方米,数据来源为中国房地产信息网。 我们先设定一组参数:无风险收益率r=5%。抵押资产初始价格与月租金比值rRP=200。对抵押资产的价格路径{Pt},在几何布朗运动的假设条件下进行模拟,模拟通过MATLAB软件编程实现,每种情况下的模拟路径均为10 000条。模型形式如下: dPt/Pt=μdt+σdWt (3) 几何布朗运动中的参数取值为:μ=0.073,σ=0.360。 表1和表2给出了不同合约期限T(单位为月,下同)和止赎房产初始价格P(单位为元/平方米,下同)下以抵押资产为标的的美式和欧式看涨期权的模拟价格。 从表1和表2可以看出,随合约期限的延长和初始价格的上升,两类期权价格均呈现出上升的趋势。另外,由于在行权时间方面有较高的自由度,美式期权的价格普遍高于欧式期权。 表1 美式期权合约模拟价格 单位:元/平方米 资料来源:中国房地产信息网,下同。 表2 欧式期权合约模拟价格 单位:元/平方米 在已经得到的美式和欧式看涨期权价格的基础上,表3展示了在不同的合约期限T和抵押资产初始价格P的条件下,商业银行出售以抵押资产为标的的美式期权,出售以抵押资产为标的的欧式期权和出租抵押资产这三种交易行为的收益情况。三种交易行为下的收益均从行权时点起以无风险收益率r = 5%为贴现率贴现到初期,以便与初始价格P进行比较。 表3 三种交易行为的贴现期望收益 单位:元/平方米 从表3的模拟结果中可以看出:美式期权可能被提前行权的时间价值,以及高于欧式期权的期权费使得出售美式期权的收益明显高于出售欧式期权;由于模拟价格路径的参数都是从实际数据(2000—2016年国内商品房平均销售价格月度数据)中估计得到的,而在此期间国内住房价格呈持续上升的趋势,因此,价格路径中的漂移率μ相对较高,导致合约到期时的止赎房产价格Pt+T有较大概率高于以无风险收益率r作为连续复利率时的商业银行最低可接受行权价K=PterT,从而使得出租抵押资产的收益高于出售欧式期权;此外,三种交易行为所得的贴现收益均高于初始价格,说明这三种交易行为均优于在收回抵押资产当期直接将其抛售的处理方法。 表4则比较了三种交易行为的Sharpe比率。从表4可以看出,由于出售美式期权的收益高于出售欧式期权,同时收益的波动差别不大,因此,出售美式期权时资产组合的Sharpe比率明显高于出售欧式期权时的情况;看涨期权空头和标的资产多头形成的抛补看涨期权组合显著降低了收益的波动,因而尽管出售欧式期权的收益低于直接出租止赎房产,但是出售欧式期权的Sharpe比率仍然高于出租止赎房产。另外,由于在参数设定中将抵押资产价格与月租金的比值rRP取为200,导致租金的收益率(6%)高于无风险收益率(5%),因此,随着合约期限的延长,三种交易行为的Sharpe比率都呈现出明显的上升趋势。 表4 三种交易行为的Sharpe比率 由于租金可能导致较长期限合约的Sharpe比率偏高,并且对三种交易行为而言都是一致的,因此,表5给出了忽略租金这一因素后三种交易行为的Sharpe比率模拟结果。 表5 三种交易行为的Sharpe比率(不考虑租金) 续表 从表5可以看出,出售美式期权所得收益更低的波动导致了更高的Sharpe比率;欧式期权的Sharpe比率绝对值大于出租抵押资产的Sharpe比率,表明出售期权所得收益的波动明显小于出租抵押资产,证明了此种金融创新工具的使用可以有效降低房地产市场的不稳定。 首先,期权的模式使得银行不仅不需要放弃止赎房产价值的上涨空间,相反还可以通过设定合适的行权价,确保自身在房价上升过程中也能得到一定的收益。 其次,银行在出售以止赎房产为标的的看涨期权后,看涨期权空头与自身持有的止赎房产多头构成了抛补看涨期权组合,能够有效降低资产组合收益的波动。因此,对于银行而言,出售以止赎房产为标的、同时附带出租条款的期权结构证券在收益波动率和Sharpe比率等方面的表现要显著优于直接将止赎房产出租的方法,能够保证银行得到更加稳定的收益。 最后,在某些特殊时期,将止赎房产作为看涨期权的标的资产出售同样可以缓解银行面临的止赎压力。银行不直接出售止赎房产可以对房价的下跌趋势形成缓冲,有助于维持市场的稳定。因此,本文设计的这种创新金融工具可以有效降低房地产市场不稳定对城市发展带来的负面影响。(三)金融资产Ⅱ
三、数值模拟方法
四、数据来源和模拟分析
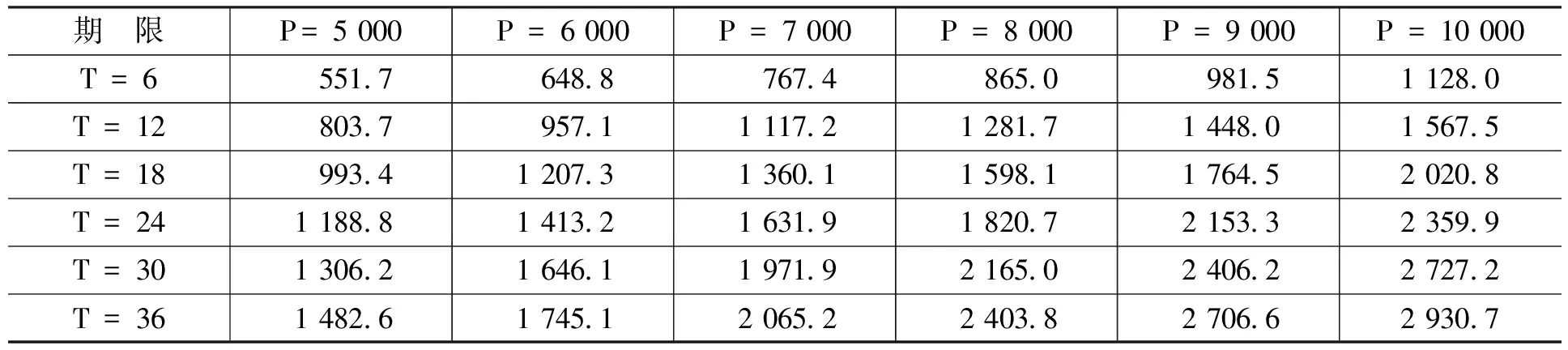
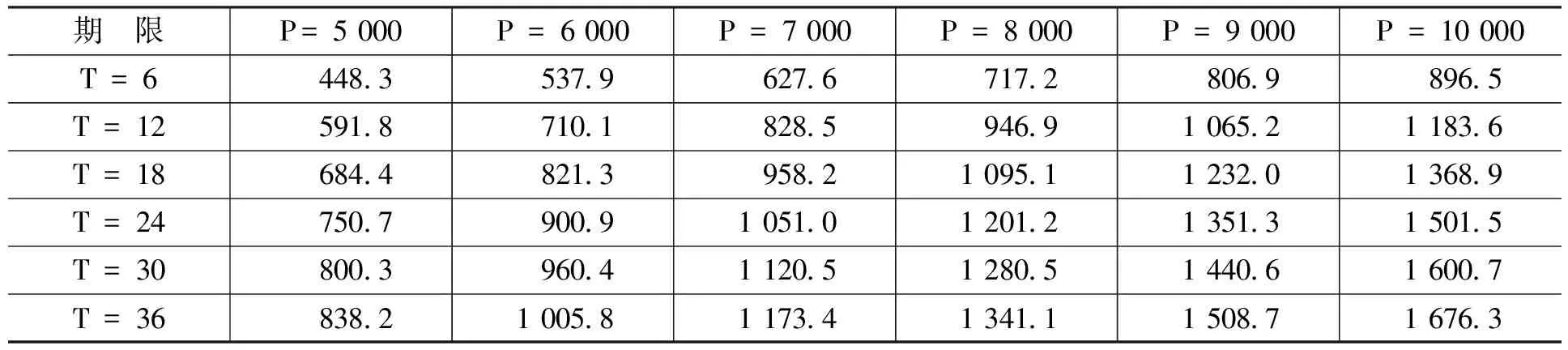
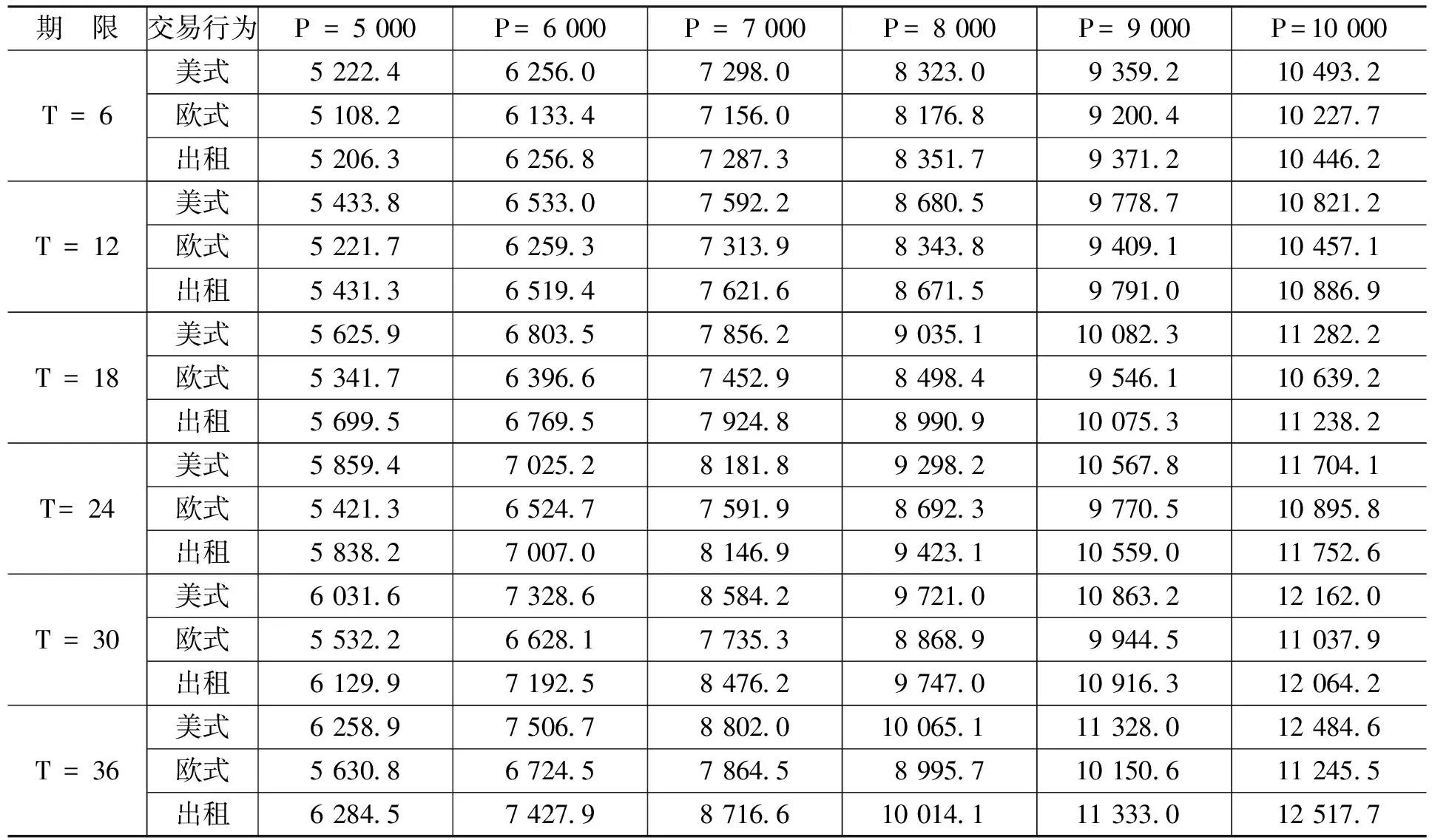

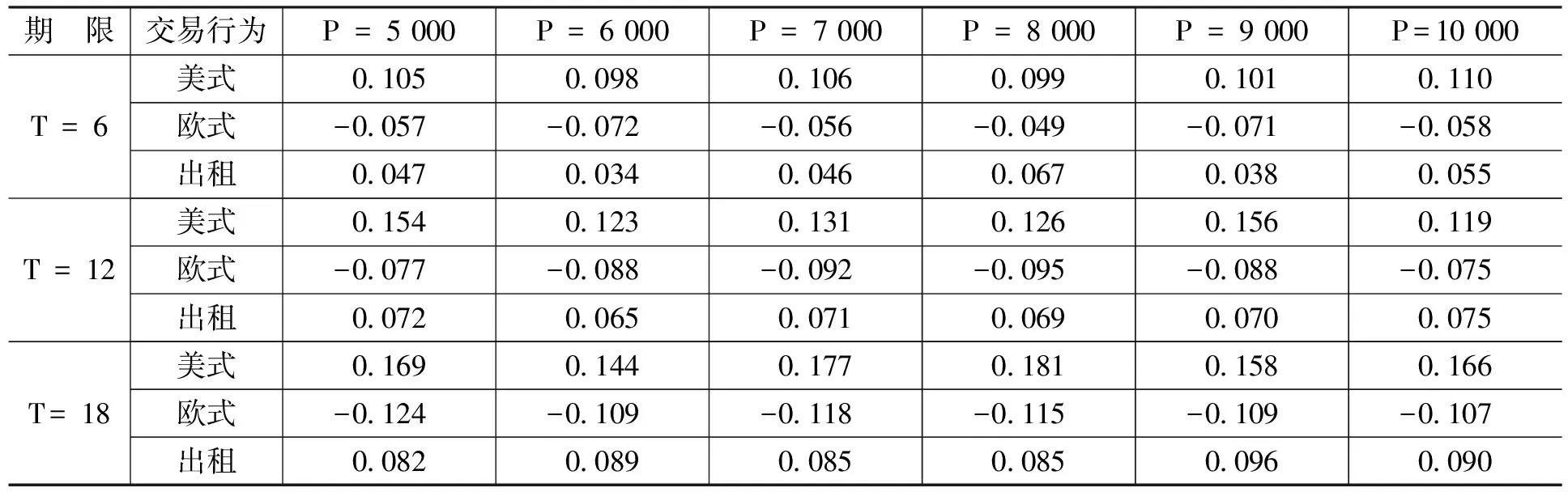
五、结 论
——基于SZH的案例研究

