弧齿线摆线圆柱齿轮副的几何参数与承载力分析

柏华文，黄文杰，宋爱平，彭云

(扬州大学机械工程学院，江苏扬州 225127)

0 引言

齿轮传动是机械传动效率最高的传动机构。在以前的研究中，圆柱齿轮的齿廓主要分为3种：渐开线、摆线、圆弧形[1]。圆柱齿轮的齿线主要分为直齿、斜齿、人字齿3种。这些齿轮都已广泛应用于机械传动。文中分析的弧齿线摆线圆柱齿轮是一种新型的圆柱齿轮,其主要特点是:齿线是圆弧的一部分[1]；齿廓分为两部分，分度圆外为一段圆弧，分度圆内为根据啮合原理所做出的齿峰圆弧的共轭曲线[2],其外形如图1所示。

图1 弧齿线摆线圆柱齿轮

对于弧齿线摆线圆柱齿轮，目前还缺少对其进行受力分析的方法，作者采用有限元分析法对齿面接触应力和齿根弯曲应力进行分析，探究弧齿线半径对其传动强度的影响。

1 弧齿线摆线圆柱齿轮的基本参数

1.1 弧齿线摆线圆柱齿轮的基本参数

1.1.1 分度圆

分度圆是为了便于齿轮设计和制造而选择的一个尺寸参考。齿轮分度圆具有标准的模数和标准的压力角，所以取它作为齿轮各部分尺寸的计算基础。取弧齿线摆线圆柱齿轮的分度圆半径为a=2l/(1+k),其中l为齿轮副中心距，k为齿轮传动比。

1.1.2 模数

在弧齿线摆线圆柱齿轮的分度圆截面处各点的周向齿厚相等、周向齿槽相等[3]，即Ts=Tc、Hs=Hc，如图2所示。这里提出一个新的齿轮参数——周向模数mc,其值为分度圆直径与齿数之比。

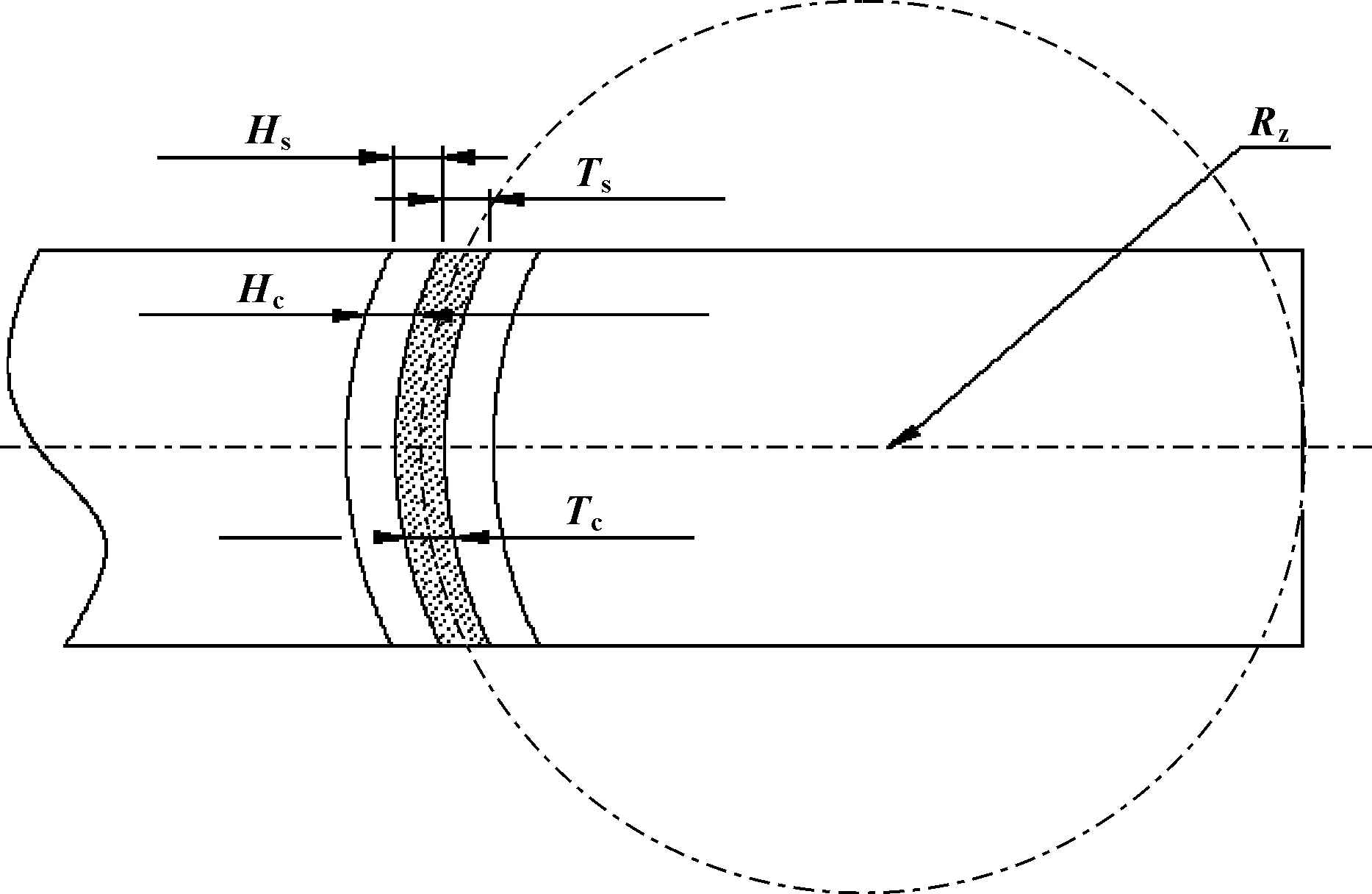
图2 弧齿线摆线圆柱齿轮几何参数

1.1.3 齿峰圆弧半径及压力角

弧齿线摆线圆柱齿轮的一些基本参数与传统渐开线齿轮的参数类似，例如，对于传统的渐开线齿轮，齿廓的不同位置有不同的压角，弧齿形摆线圆柱齿轮也具有相同的特性。在图3(a)中，齿峰为一段圆弧，力Fn朝向圆弧中心O3。假设βi是旋转角，ai是齿峰圆的半径，而αi是相应的压力角。

如图3(a)所示，根据三角形的正弦定理:

(1)

一对啮合齿轮在分度圆处具有相同的压力角，k是传动比。假设齿轮1和齿轮2是一对啮合齿轮。如图3(b)所示，r1表示齿轮1齿峰圆的半径，b1代表从齿轮的中心到齿峰圆弧的中心长度，a1表示齿轮1的分度圆半径。齿峰圆弧的一半所对应的角度β1=π/2z1，齿谷摆线的一半所对应的角度也是相同的角度β2=π/2z1(其中z1为齿轮1的齿数)。在图3(b)中，根据方程(1)，可以得到以下方程：

(2)

由图3(c),同理可得与齿轮1相啮合的齿轮2的方程:

(3)

其中：α表示齿轮1的节圆压力角,γ和α是互余的角度。a2=ka1,b2=kb1,β2=π/2z2。

图3 弧齿线摆线圆柱齿轮压力角

1.2 齿廓方程

1.2.1 齿峰曲线方程

参照图4，建立了一种笛卡尔坐标系XO1Y，假设齿数比k=z2/z1，齿轮1作为传动齿轮。在△O1O3S1中，根据三角形的余弦定理：

(4)

齿轮1的半齿峰圆弧T1S1的参数方程可以表示为：

(5)

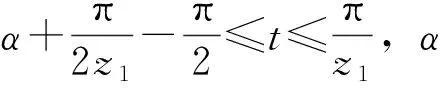
图4 齿轮副啮合齿廓

1.2.2 齿谷曲线方程

由图5可知：当齿轮1沿着中心O1顺时针旋转角度θ,齿轮2将沿着中心O2逆时针旋转角度θ/k。令齿轮2逆时针旋转并令齿轮1不动。齿轮2曲线T2S2和齿轮1曲线Q1S1相啮合,G(x2，y2)是啮合点，P是两个齿轮节圆的交点。啮合点G的法线必然穿过齿轮2的齿峰圆中心点O4以及节点P。因此，点G、P、O4在直线GO4上。让直线O1F∥O4G,F是直线O1F和直线O2O4的交点,δ是直线O1F和X轴的夹角。让EF垂直于笛卡尔坐标系的X轴，E为垂足，让直线O4A平行于X轴，A是交点。让CG垂直于直线AC,C为垂足。通过几何关系，可以得到以下关系：△O1FE∽△O4GC, △O2PO4∽△O2O1F, △O2O4A∽△O2FD，可以得出以下结论:

∠GO4C=∠FO1E=δ

(6)

(7)

(8)

(9)

O1F=(O1E2+FE2)1/2=

(10)

图5 任意旋转角度下的齿谷摆线的啮合

齿轮1的齿谷摆线的1/2可以用笛卡尔坐标系表示为下面的方程：

x2=O1B-O4A-O4C=(k+1)·a1·cosθ-

(11)

y2=O2B-O2A+GC=(k+1)·a1·cosθ-

(12)

其中：

1.2.3 齿线半径与位置角的关系

如图6所示，有笛卡尔坐标系(O,X,Y,Z)。XOY平面穿过齿轮中间部分，Z轴与齿轮轴重合。将横向剖面投影到中间部分，齿轮的中间部分可以被视为齿廓。

假设B是齿轮的齿宽，RZ是圆弧齿的半径。弧齿线位置角对应弧长的方程为：

(13)

图6 齿线位置角φ2与齿轮的周向展开

可以算出位置角φ2为：

(14)

其中：a为分度圆半径。

1.3 重合度

重合度是齿轮传动的一个很重要的概念,是齿轮传动的连续性及平稳性评价的重要指标。实际啮合线的长度与周节的比值称为重合度。参照人字齿轮副重合度的计算方法，弧齿线摆线圆柱齿轮的重合度ε由端面重合度εα和轴向重合度εβ组成[4]，即

ε=εα+εβ

(15)

由于弧齿线摆线圆柱齿轮的齿廓比较特殊，用一般齿轮副重合度的计算方法比较困难，所以作者采取了重合度的另一种定义方法。首先介绍几个概念：

齿轮作用角[5]:轮齿从开始啮合到终止啮合所转过的角度, 用φ1表示。

周节圆心角:一个周节所对的圆心角，齿轮上不同圆(Ri)其周节(pi)是不同的,但是所有不同周节(pi)所对圆心角都是相同的[6],用φ表示,即

φ=2π/z

(16)

重合度定义为:齿轮作用角φ1与周节圆心角φ之比[6]。即:

(17)

周节圆心角与齿轮作用角的示意图如图7所示。

图7 周节圆心角与齿轮作用角

因此，可以得到以下方程:

(18)

方程(18)表明：弧齿线摆线圆柱齿轮的端面重合度是常数,其值0.5。弧齿线摆线圆柱齿轮的轴向重合度εβ可以按弧线圆柱齿轮的轴向重合度[7]计算：

(19)

由式(18)和式(19)可以得到：

(20)

为了确保齿轮传动可以持续和平稳,因此ε≥1,方程(20)重写为:

RZ≤(B2+m2π2)/(4πm)

(21)

如方程(21)所示，增加B值或降低值RZ可以达到增加重合度ε值的目的。然而，如果RZ太小，则会导致正常的齿轮两端法向厚度太薄，使得齿轮抗弯强度变弱[8]。如果RZ过大，弧齿轨迹与直线相似，不能体现弧齿的优点，而且可能会使重合度小于1。此外，RZ的值通常大于B值的一半，因此RZ值的范围可以表示为:

B/2≤RZ≤(B2+m2π2)/(4πm)

2 弧齿线摆线圆柱齿轮副受力分析

由工业经验和实验室实验数据可知，两个高应力区域通常是渐开线齿轮失效的根源。这两个区域是齿轮的齿根和齿轮的接触表面[9]。利用三维建模软件SolidWorks对一组弧齿线摆线圆柱齿轮副及渐开线直齿圆柱齿轮副进行齿面接触受力分析。选定弧齿线摆线圆柱齿轮副的几个参数：

(1)模数m为4 mm;

(2)小齿轮齿数z1为24;

(3)大齿轮齿数z2为48;

(4)齿轮宽度B为40 mm;

(5)齿线RZ半径分别为24、26、30、32、34 mm;

(6)齿轮材料为合金钢。

并添加约束，施加同样大小的传动转矩1 000 N·m，在外界条件相同的情况下，对齿轮啮合面进行接触面选择，然后划分网格，最后进行受力分析。渐开线直齿齿轮副传动采用同样参数及步骤进行比较。RZ=34 mm时的弧齿线摆线圆柱齿轮副的应力图如图8所示，渐开线直齿圆柱齿轮副应力图如图9所示。在接触齿侧的弯曲应力被认为是拉应力，而对齿侧的弯曲应力则被认为是压应力。其余弧齿线半径的应力数值结果统计如表1所示。

图8 RZ=34 mm的弧齿线摆线圆柱齿轮副静应力分析

图9 直齿圆柱齿轮副静应力分析

表1 静应力有限元分析结果MPa

3 结论

以上阐述了弧齿线摆线圆柱齿轮的基本参数并利用有限元分析法对其齿面接触应力和齿根弯曲应力进行了分析，可以得出以下结论:

(1)弧齿线摆线圆柱齿轮的接触应力及弯曲应力随着弧齿线半径RZ的增大而逐渐减小。

(2)与渐开线直齿轮相比，当RZ为30、32、34 mm时(当弧齿线半径RZ大于34 mm时，齿轮副重合度小于1，无法正常传动，故未考虑RZ大于34 mm的情况)，在其他条件相同情况下，弧齿线摆线圆柱齿轮的最大接触应力分别减少了5.63%、8.94%、25.07%，弧齿线半径RZ越大，减小的百分比也越大。

(3)与渐开线齿轮相比，RZ为30、32、34 mm时，弧齿线摆线圆柱齿轮的齿根弯曲拉应力分别比渐开线齿轮低12.97%、16.06%、23.52%，齿根弯曲压应力分别降低了11.12%、17.22%、24.14%。弧齿线半径RZ越大，减小的百分比也越大。

(4)在保证齿轮副传动重合度大于1的情况下，弧齿线RZ取值在0.75B～0.85B内时，与渐开线圆柱齿轮相比，弧齿线摆线圆柱齿轮具有更小的齿面接触应力与齿根弯曲应力，具有比较好的接触疲劳强度、弯曲疲劳强度和更长的使用寿命。