线上零售商退款保证下供应链定价与合同设计

张旭梅， 金 亮，2

(1．重庆大学 经济与工商管理学院，重庆 400030;2．南昌大学 经济管理学院，江西 南昌 330031)

1 引言

随着(移动)互联网的快速普及和消费者线上购物意愿的不断提高，以亚马逊、阿里巴巴、京东等为代表的电商企业得到飞速发展［1，2］。2016年全球电商零售额达 1．9万亿美元，增长率达23．7%［3］，2016 年上半年中国网络零售市场交易规模达2．3 万亿元，同比增长 43．4%［4］，线上购物已成为消费者的主要购物渠道之一。但由于消费者在线上购买不能对产品有所体验，使得消费者收到的产品有可能与其预期不匹配，由此导致较高的产品退货率，有研究表明电商平均退货率达22%［5］。并且，当消费者发生退货时，线上零售商往往需要给予消费者全额退款［6］，从而造成退货损失。由于线上零售商直接面对消费者，因而相关的消费者退货信息往往为线上零售商的私有信息，由此易导致线上零售商和上游制造商决策激励失调，影响整个供应链的利润。因此，在退款保证下，消费者退货行为会对线上零售商的定价策略产生何种影响?提供退款保证是否对消费者有利并提升线上零售商的利润?制造商又该如何设计不对称信息下的产品批发合同?这一系列问题都需要研究和解决。

目前，有关退款保证的研究主要从企业是否应该提供退款保证以及退款保证对企业的影响等方面展开。Mann 和 Wissink［7，8］较早地研究了退款保证问题，指出企业向消费者提供退款保证能够有效降低消费者购买风险，进而得出企业提供退款保证的可行条件;Chen和Bell［9］考虑消费者退货数量受到产品销售量和销售价格的联合影响，研究了退款保证对企业最优定价和订货量的影响;McWilliams［10］针对由两个质量差异化竞争企业构成的寡头垄断市场，研究了竞争性退款保证策略选择问题;黄宗盛等［11］同样针对存在质量差异化的寡头垄断市场，研究了产品质量差异化对竞争性零售商退款保证策略选择的影响;Akcay等［12］考虑零售商能够以一定折扣价将消费者退货的产品进行二次销售，研究了退款保证对零售商最优定价与订货策略的影响;Hsiao和Chen［13］比较分析了提供退款保证和免退货成本政策对销售商利润的影响，进而考察了这两种退货政策的可行条件，认为当消费者对产品的估值较高时，提供退款保证才有利;Qin等［14］研究了存在策略消费者情形下的退款保证策略选择问题;Heydari等［15］针对由一个供应商和一个零售商组成的供应链，研究了零售商的最优订货决策和退款保证策略选择问题。上述文献研究的均为线下销售渠道的退款保证策略选择及其有关影响问题。近年来，有关线上销售渠道的退款保证策略选择问题也逐渐引起学者们的关注。例如，黄宗盛等［16］研究了其线上、线下渠道的竞争性退款保证策略选择问题;Chen等［17］同样针对线上、线下渠道，研究了单渠道情形和双渠道情形下的零售商退款保证策略选择问题，并考察了线上销售渠道的个性化定价策略;Gao 和 Su［18，19］针对一个实施了“线上购买，线下取货”策略的全渠道零售商，研究了退款保证下的线下销售渠道最优库存决策问题。上述考虑了线上销售渠道退货保证的文献均以单个企业为研究对象，且都基于完全信息背景。不同的是，本文从供应链视角，针对由一个制造商和一个线上零售商组成的供应链，考虑线上零售商在其线上销售渠道提供退款保证，研究消费者退货成本信息不对称下的供应链定价与合同设计问题。

鉴于此，本文以一个制造商和一个线上零售商组成的供应链为研究对象，考虑在线上零售商提供退款保证下可能存在的消费者退货行为，根据消费者效用理论建立受消费者退货成本影响的需求函数，构建消费者退货成本信息对称与不对称下的供应链博弈模型，研究线上零售商定价与制造商合同设计问题。进而分析不对称信息对线上零售商最优定价与制造商合同设计的影响，考察退款保证对供应链均衡、供应链成员利润以及消费者剩余的影响。不同的是，本研究综合考虑了线上零售中可能存在的消费者退货行为和供应双方信息不对称，且由一般的利润视角扩展至消费者剩余视角。

2 问题描述

考虑由一个制造商(M)和一个线上零售商(O，以下简称“零售商”)组成的供应链。其中零售商向制造商订购一种产品，然后通过其线上销售渠道销往市场，零售价格为p。

假设市场上的每个消费者至多购买1单位的产品。消费者在收到零售商配送的产品前，对于产品是否符合其需求不确定，如服装尺寸不符、产品实物与预期不符等，故假设产品符合消费者需求的概率为 λ(0 ＜ λ ＜1)［6，10］。若产品符合消费者需求，消费者能够获得效用v－p，其中v为消费者对符合其需求产品的支付意愿，v服从区间［0，1］上的均匀分布［17，20］;若产品不符合消费者需求，则消费者选择退货并获得全额退款，但消费者会产生相应的退货成本 t(如退货的物流费用等)［17］。由此，得到消费者购买产品的预期净效用为

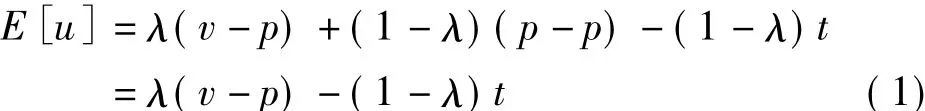
消费者根据max{E［u］，0}来选择是否购买产品。当 E［u］≥0，即 v≥p+(1 －λ)t/λ 时，消费者才会购买。由此，可以得到产品需求为

其中f(v)为v的概率密度函数。

在制造商与零售商合作过程中，考虑零售商直接面对消费者并接收消费者退货的产品，因而消费者退货成本为零售商的私有信息，远离市场的制造商并不能准确观测消费者退货成本大小，故假设消费者退货成本存在两种可能:低退货成本tL(L类型)和高退货成本tH(H类型)，tL/tH＜1。并且，消费者退货成本为L(H)类型的概率为ρ(1－ρ)，这是供应双方的共同知识。为此，制造商根据消费者退货成本类型i(i=L or H)来设计一组合同菜单{wL，fL}和{wH，fH}以供零售商选择，其中 wi为产品批发价格，fi为零售商向制造商支付的一次性转移支付，如特许经营费、加盟费等。

假设制造商的边际生产成本为常量，为便于分析且不失一般性，标准化为零。消费者退货行为均会给零售商和制造商造成退货损失［21］，本文分别用rM和rO来表示单位退货产品给制造商和零售商带来的退货损失。根据上述假设，可以得到制造商和零售商的利润函数分别为

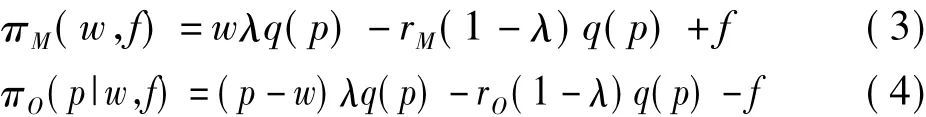
3 模型分析

采用逆向归纳法，先分析零售商的产品定价策略，然后再分析制造商的合同设计。

3．1 零售商的最优定价策略

当消费者类型为i(i=L or H)时，给定合同{wi，fi}，零售商以自身利润最大化为目标决策最优产品零售价格。得到零售商面临的优化问题为

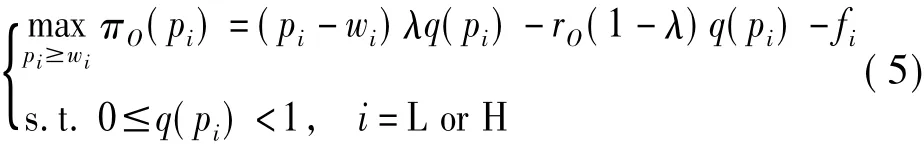
求解问题(5)，得到如下引理。

引理1 给定合同{wi，fi}(i=L or H)，零售商的最优定价策略为

证明 容易验证πO(pi)为关于pi的凹函数，故根据一阶条件即可得。

引理1表明，在给定制造商合同下，零售商的最优定价决策仅与批发价格、产品符合消费者需求的概率、消费者退货成本以及零售商退货损失有关联。

3．2 对称信息下的制造商最优合同设计

对称信息下，制造商知道消费者类型为i(i=L or H)，并设计合同{wi，fi}。此时，制造商需要解决如下优化问题。本文用字符“N”表示“对称信息”。

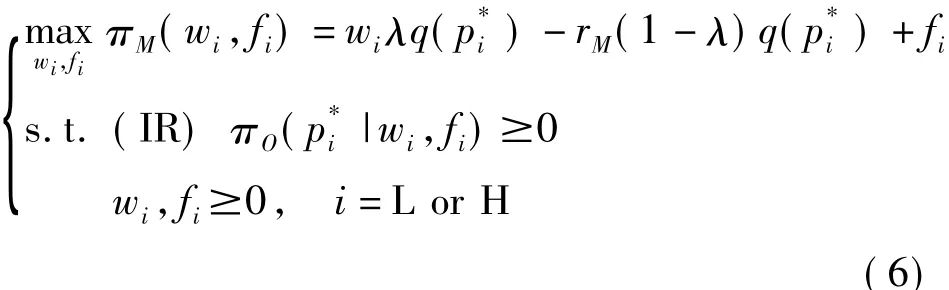
问题(6)中，约束式(IR)为个体理性约束，本文假设制造商知道零售商的保留利润为零。那么，约束式(IR)表示零售商获得的利润不能小于其保留利润。采用KT方法求解，得到如下定理。

定理1 取γ=λ－(1－λ)(rM+rO)，则对称信息下最优合同设计

命题1 对称信息下最优产品零售价格、供应链系统利润和消费者剩余均能达到集中式决策下的最优值，即本文用字符“C”表示“集中决策”。

证明略。

命题1表明，在对称信息下，制造商通过“批发价格+一次性转移支付”的合同设计能够实现供应链的完美协调。并且，此时消费者的退货行为却也会导致供应链系统利润的损失。

3．3 不对称信息下的制造商最优合同设计

不对称信息下，制造商在设计合同时还需甄别消费者类型。此时，制造商面临如下优化问题。本文用字符“A”表示“不对称信息”。

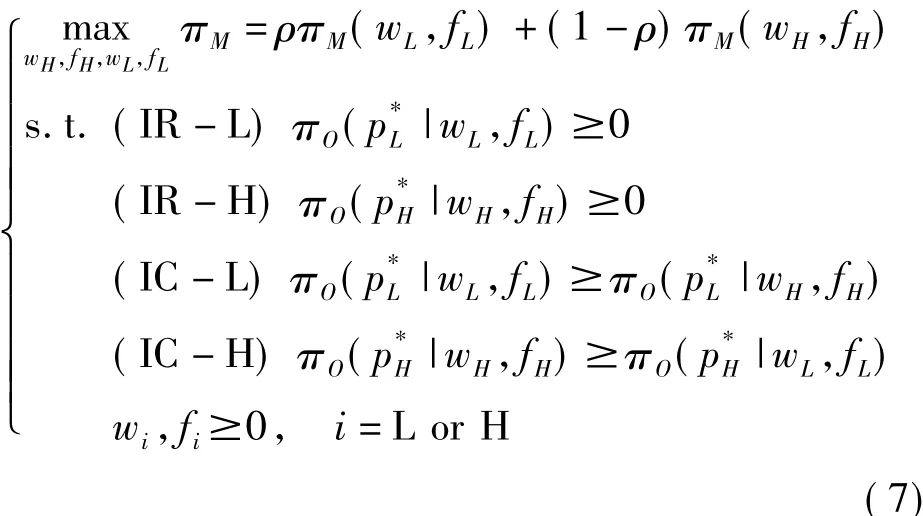
问题(7)中，πM为制造商在两种类型消费者下获得利润的期望。约束式(IR－i)为个体理性约束;约束式(IC－i)为激励相容约束，以保证零售商如实选择合同，其中表示当消费者为L(H)类型时，零售商谎报并选择合同{wH，fH}(wL，fL)获得的利润。

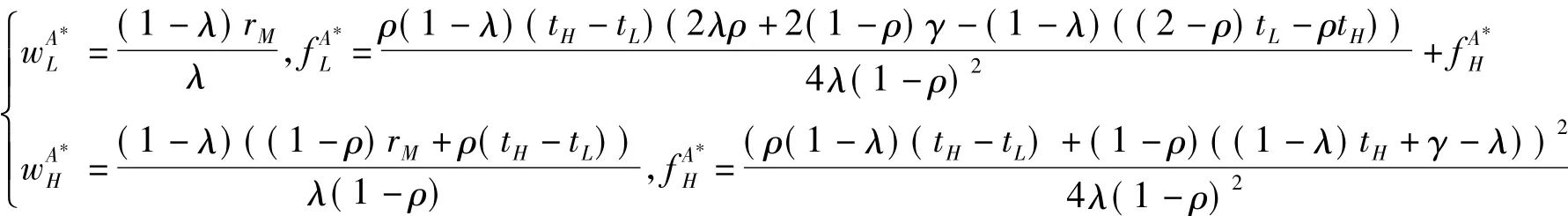
证明 制造商为最大化自身利润，会尽可能地降低fL和fH而使约束式(IR－H)和(IC－L)取等号，即为紧约束，可得fH和fL的表达式。将fL和fH代入πM，易知πM(wH，wL)的 Hessian矩阵 H 负定，即存在唯一最优解，故根据一阶条件可求得

定理2表明，针对不同类型的消费者，制造商设计了一组合同菜单来甄别零售商拥有的私有信息。由约束式(IC－L)和(IR－H)为紧约束可知，在给定的批发价格和下，一次性转移支付也是确定的。最后，在不对称信息下，当消费者为i类型时，用来表示最优产品零售价格和产品需求;别表示零售商和制造商获得的利润以及消费者剩余。

命题2 消费者退货行为对制造商和零售商定价策略存在如下影响:

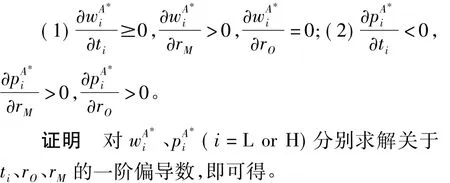
命题2表明，随着消费者退货成本的增大，若消费者为L类型，则制造商的最优批发价格决策不受影响;若消费者为H类型，则制造商会提高批发价格;但对零售商而言，由于消费者退货成本对产品需求不利，故零售商会降低产品零售价格来刺激销售。当消费者退货给制造商造成的损失较大时，制造商将会提高批发价格来弥补其部分损失，由此也导致零售商相应地提高产品零售价格。

4 信息价值与退款保证价值分析

4．1 信息价值

为考察信息价值，先令对称信息(不对称信息)下的制造商、零售商以及供应链系统的期望利润分别为则可得零售商信息租金为;制造商信息价值为供应链损失

命题3 制造商信息价值、零售商信息租金以及供应链损失有如下关系:

(1)ΔπM＞0，ΔπO＞0，ΔπSC＞0;(2)ΔπM=ΔπSC+ΔπO。

证明 根据定理1，2，直接比较易得。

命题3表明，不对称信息的存在对供应双方的影响都会造成制造商、零售商以及供应链系统期望利润的变化。当消费者为L类型时，制造商需要通过一次性转移支付给予零售商一定的“信息共享费”，由此可以使供应链系统利润达到最优水平当消费者为H类型时，制造商需要设计较高的批发价来规制零售商如实选择合同由此导致制造商利润损失，零售商能够获得更多利润，这也造成了供应链系统利润的损失。并且，制造商信息价值同时包含了零售商信息租金和供应链损失，这也意味着制造商可以通过权衡零售商信息租金和供应链损失来实现自身期望利润最大化。此外，还可以发现，不对称信息的存在有可能会导致消费者剩余的损失，仅当消费者为L类型的概率较低时，不对称信息的存在才会给消费者剩余带来不利。

在本文研究的供应链模型中，考虑在制造商与零售商的长期合作中，制造商往往具有一定的谈判力，并假设制造商的谈判力为δ，则零售商的谈判力为(1－δ)。下面将从谈判的角度来进一步讨论信息价值。为简化表达，先定义:

命题4 (1)当消费者为L类型时，制造商通过支付“信息共享费”可以实现供应链系统利润最优，故零售商不会与制造商达成谈判;(2)当消费者为H类型时，若制造商的谈判力满足δ≤δ≤1，则具有信息优势的零售商会愿意披露其拥有的私有信息，从而与制造商分享整个供应链的利润。

证明 当消费者为H类型时，供应双方达成谈判需满足:一是零售商谈判所得的利润需要满足=0，故在 0≤δ≤1 条总是成立;二是制造商谈判所得利润需要满足可求得 δ≥δ。因此，可得供应双方达成谈判的条件为δ≤δ≤1。

命题4表明，在不同的市场条件下，制造商并不总是能够与零售商达成谈判。当消费者为L类型时，为激励零售商根据消费者类型如实选择合同，制造商需要向零售商支付等量的信息租金作为“信息共享费”，故而制造商与零售商之间不能达成谈判。当消费者为H类型时，制造商通过权衡零售商信息租金和供应链损失，使得零售商仅能获得其保留利润，因此零售商总是愿意谈判。具体分析，在H类型消费者下，仅当制造商的谈判力满足条件时，供应双方才能达成谈判。

4．2 退款保证价值

为分析零售商退款保证的价值，先给出没有退款保证情形下的供应链定价与合同设计。在没有退款保证情形下，消费者购买产品获得的预期净效用为由此可得产品需求为，制造商和零售商的利润函数分别为通过求解，得到制造商的最优合同设计为并获得利润λ/4;零售商的最优定价决策为p^*=λ/2，获得利润消费者剩余为

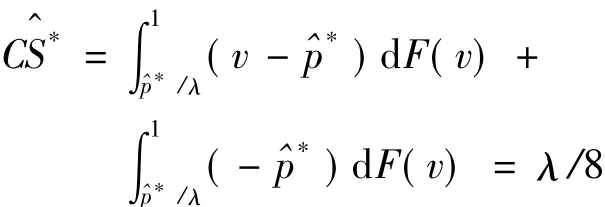
命题5 取κ=λ+rM+rO，则退款保证对零售商最优定价与产品需求有如下影响:

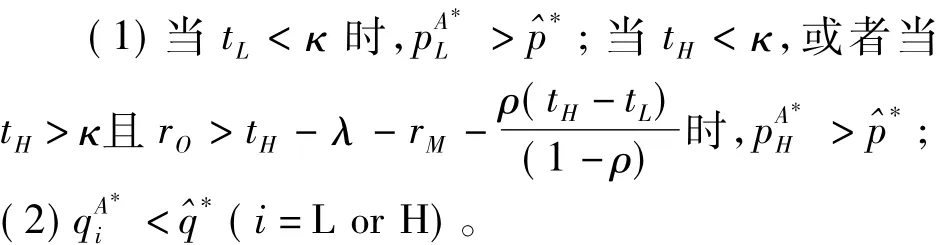
由命题5可知，在提供退款保证情形下，若消费者退货成本较低，则零售商会实施高价策略。并且，退款保证对零售商最优定价策略的影响取决于消费者退货成本以及制造商、零售商的退货损失。该命题表明，尽管退款保证能够在一定程度上缓解消费者购买产品的不确定性，但由于退货成本的存在，退款保证反而会导致产品需求的降低，消费者有可能需为此支付一定的溢价。

证明 (1)根据定理2和定理3，比较不同退款保证情形下的制造商与零售商期望利润，得到:其中g(ρ)=Aρ2+Bρ+C，A=(1 － λ)(tH－tL)2＞0，B=ξ＞0，C= －ξ＜0。由此易知，－B/A＜0，C/A＜0，故 g(ρ)存在一正一负两个实根，并且，容易求得正根为ρ珋1。进而比较 ρ珋1与1的大小，可以验证:当 ρ=0时，g(0)=C＜0;当ρ=1时，g(0)=(1－λ)(tH－tL)2＞0，故有 ρ珋1＜1。因此，当 ρ珋1＜ ρ＜1时，－

(2)同理，根据消费者类型的不同，分别比较消费者剩余，易得。

命题6表明，退款保证对制造商利润和消费者剩余的影响存在一定的不确定性，但零售商总是能够获得更多的利润。与没有退款保证情形相比，退款保证的影响有:其一，消费者退货行为会给制造商和零售商带来退货损失，影响二者的最优定价决策，并导致产品需求的降低;其二，消费者退货成本为零售商的私有信息，因而信息优势零售商可以获得信息租金。综上两方面的影响，仅当消费者为L类型的概率较大时，退款保证才能有效提升制造商的利润;而对于零售商，单纯地从提供退款保证中并不能获得额外收益，但退款保证能够使零售商拥有信息优势，并据此获得额外的信息租金。此外，退款保证虽然能够在一定程度上缓解消费者的购买风险，但由于消费者退货成本的存在以及可能要为退款保证支付的溢价，在一定条件下提供退款保证反而对消费者剩余不利。

5 算例分析

本节将通过数值算例来直观考察上述理论分析结果，以得到更多管理学启示。设置参数:tL=0．1，tH=0．2，rO=0．25，rM=0．4，ρ=0．5。以 λ 为横坐标，绘制图1～图3。

观察图1可以发现:在不对称信息下，随着λ的增大，制造商和供应链系统的期望利润随之增大，而零售商的期望利润先增大后减小，表明较低产品退货率总是对制造商有利;随着λ的变化，制造商期望利润比零售商期望利润的变化更为显著，表明零售商可以通过调整产品零售价格来缓解产品退货率对其期望利润造成的不利影响。

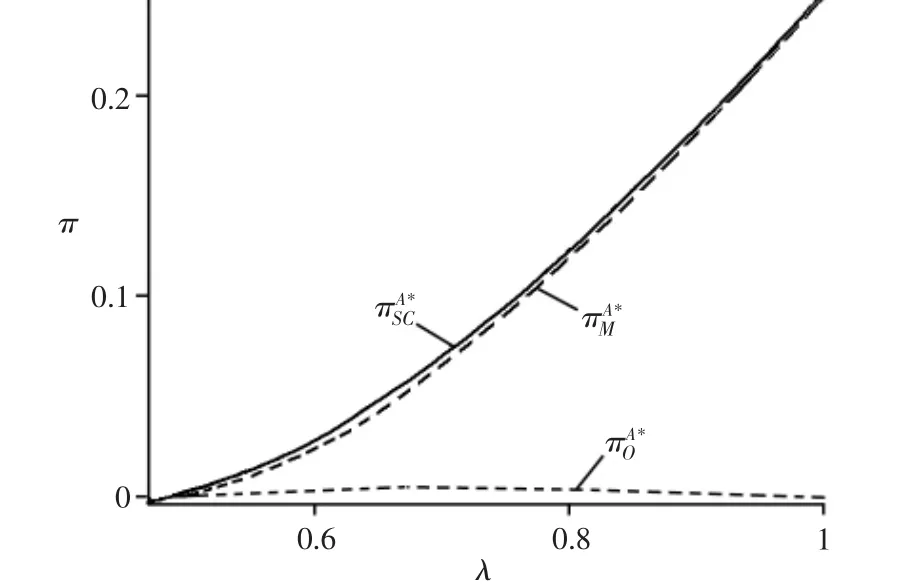
图1 供应链成员及供应链系统期望利润

观察图2可以发现:在不同情形下，L类型消费者的消费者剩余总是会随λ的增大而增大，并且不对称信息的存在并不会影响L类型消费者的消费者剩余;不提供退款保证情形下的消费剩余总是高于提供退款保证情形下的值，表明提供退款保证并不一定对L类型消费者有利。

图2 消费者为L类型时的消费者剩余

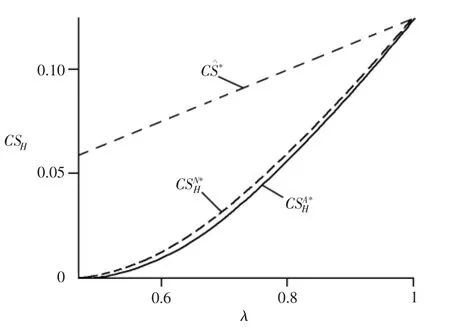
图3 消费者为H类型时的消费者剩余

观察图3可以发现:在不同情形下，H类型消费者的消费者剩余总是会随λ的增大而增大，且不对称信息的存在有可能会影响H类型消费者的消费者剩余;结合命题6，当ρ=0．5＜珋ρ2时，不提供退款保证情形下的消费者剩余总是更高，表明此时退款保证并不能提升消费者剩余。

6 结论与展望

本文针对由一个制造商和一个线上零售商组成的供应链，考虑消费者可能存在的退货行为以及零售商向消费者提供退款保证，建立了消费者退货成本信息对称与不对称下的供应链博弈模型，研究了零售商的最优定价策略与制造商的最优合同设计，进而考察了不对称信息和退款保证对供应链均衡、供应链成员利润以及消费者剩余的影响。本文所得结论为以下三个方面:

(1)对称信息下，制造商通过“批发价格+一次性转移支付”的合同设计能够实现供应链的完美协调，但可能存在的消费者退货行为总是会造成供应链系统利润损失;不对称信息下，制造商的最优合同设计需要同时考虑对零售商最优定价策略的影响和满足零售商的参与约束;随着制造商和零售商退货损失的增大，二者均会实施高价策略来弥补自身的退货损失，同时较高的产品批发价格也会促使零售商实施高价策略。

(2)不对称信息对供应双方最优决策的影响会使得制造商和零售商的利润发生变化，但不一定会造成供应链系统利润损失，有可能仅导致收益在供应链系统内部的重新分配;制造商可以通过权衡零售商信息租金和供应链系统利润损失来设计合同菜单，以最小化自身信息价值，从而实现自身期望利润最大化;当消费者退货成本较低(即为低类型)时，制造商通过支付“信息共享费”可以实现供应链系统利润最优;当消费者退货成本较高(即为高类型)时，若制造商的谈判力满足一定条件，则具有信息优势的零售商会自愿披露其拥有的私有信息使得供应链系统利润达到最优(对称信息下的值)，此时供应链成员将共同分享整个供应链系统利润，且二者获得的利润均能得到有效提升。

(3)零售商向消费者提供退款保证服务在一定程度上能够缓解消费者在线上渠道购买产品的不确定性，但消费者也有可能需为此支付一定的溢价，并导致产品需求的降低，此时消费者剩余有可能降低;提供退款保证尽管不能给零售商带来额外收益，但可以使零售商拥有信息优势，并据此获得额外的信息租金;对于制造商而言，退款保证并不一定能够提高其利润水平。

本文研究的供应链仅包含一个线上零售商，现实中一个制造商往往会同时通过多个线上零售商来销售产品，因此，研究包含多个线上零售商的供应链，即竞争环境下存在不对称信息的供应链定价与合同设计问题是未来可以进一步研究的方向。