具有脉冲入侵的Lotka-Volterra捕食系统的动力学分析
甘静雯,李 帅,宋新宇
(1. 北京林业大学 生物科学与技术学院 生物计算中心, 北京 100083;2. 信阳师范学院 数学与统计学院, 河南 信阳 464000)
0 引言
最近,微分方程理论在数学生态学方面的应用已经得到了快速地发展.捕食者与被捕食者之间的竞争和合作的模型已经被很多学者研究[1,2].有关种群动力学最著名的模型之一是Lotka-Volterra竞争捕食系统,捕食是影响着生态系统种群动力学一个重要的生物进程[3,4].值得关注的是两斑块之间种群的扩散将会影响种群动力学模型的动力学性质,前期描述传播扩散的种群动力学模型大多是连续模型[5],但是在现实中,种群的扩散通常具有脉冲性质[6],例如每年固定时期植物种子扩散和入侵.因此将脉冲扩散引入数学模型中可以能够很好地描述这一自然现象.本文将研究具有脉冲效应的捕食系统,即在某些时期一个斑块的捕食者入侵另一个斑块竞争食饵,当食饵的数量急剧减少时就对食饵进行投放,利用类似文献[7,8]的方法,给出系统解的有界性、解的稳定性和系统的持久性.
1 模型的建立
考虑下面Lotka-Volterra捕食系统:
(1)
这里x和y分别是食饵和捕食者的种群密度,参数a1、b1、d1、k、β是正常数.
由于在实际生活中,种群之间存在多种竞争关系,一个地方的物种会入侵另一个地方,并与本地物种竞争食饵.与此同时,在一定时期对食饵进行投放.本文考虑捕食者成比例的迁移,以及食饵成比例投放.即在一个时间段内第二斑块部分捕食者迁移到第一斑块,在另一时间段内对食饵进行投放.考虑这些迁移和投放因素后,系统(1)改成如下形式:
(2)
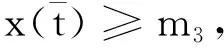
其中:种群x(t)和y(t)分别为第一斑块的食饵和捕食者的种群密度.z(t)是第二斑块捕食者的种群密度.z(t)和y(t)属于同种性质的种群,x(t)的内禀增长率和密度制约项分别是a1,b1.a1/b1是种群最大承载能力.种群x(t)和y(t)是捕食关系,β是捕食系数,k是y(t)的转化率且0 首先讨论系统(2)解的正性,由脉冲微分方程解的存在性定理可知,系统(2)存在满足初始条件的(x(t),y(t),z(t)). 下面引理容易证明. 引理1 假设u(t)是系统(2)的一个解,若u(0)≥0,则对所有的t≥0,有u(t)≥0;若u(0)>0,则对所有的t>0,有u(t)>0. 引理2 存在一个常数M>0,使得当t足够大时,系统(2)的任一解x(t)≤M,y(t)≤M,z(t)≤M. 证明定义 V(t)=x(t)+y(t)+z(t), 由于α D+V(t)+αV(t)=(a1+α)x-b1x2-βxy+kβxy- (b1-α)y+(a2+α)z-b2z2≤ (a1+α)x-b1x2+(a2+α)z-b2z2= 这里 又由于0<ε≤1,所以当t=(n-1+l)τ时,有 V((n-1+l)τ+)=x((n-1+l)τ)+ y((n-1+l)τ)+ εdz((n-1+l)τ)+(1-d)z((n-1+l)τ)= x((n-1+l)τ)+y((n-1+l)τ)+ z((n-1+l)τ)-(1-ε)dz((n-1+l)τ)≤ x((n-1+l)τ)+y((n-1+l)τ)+ z((n-1+l)τ)=V((n-1+l)τ), 当t=nτ时,有 V(nτ+)=x(nτ+)+y(nτ+)+z(nτ+)= (1+p)x(nτ)+y(nτ)+z(nτ)≤ V(nτ)+px(nτ)≤(1+p)V(nτ), 其中x(nτ)≤V(nτ).假设(1+p)V(nτ)≤V((n-1+l)τ+).由于t∈((n-1)τ,(n-1+l)τ]和((n-1+l)τ,nτ],当t→时V(t)→ξ/α,所以V(t)一致最终有界.因此通过V(t)的定义,存在一个常数M>0,使得当t足够大时,x(t)≤M,y(t)≤M,z(t)≤M.证毕. 若x(t)=0,则系统(2)存在子系统: (3) 系统(3)在脉冲之间的解析解如下: (4) 考虑到系统(3)的第三和第四个方程,可以得到系统(3)的频闪映射: (5) 所以差分方程(5)有两个固定的不动点,分别是G1(0,0)和G2(y*,z*),即 (6) 定理1 (i)如果(1-d)ea2τ<1,那么差分方程(5)的不动点G(0,0)是全局渐近稳定的; (ii)如果(1-d)ea2τ>1,那么差分方程(5)的不动点G(y*,z*)是局部渐近稳定的. 证明为了方便,记 (yn,zn)=(y((n+l)τ+),z((n+l)τ+)), 差分方程(5)的线性形式可以写成 (7) 显然G1(0,0),G2(y*,z*)由方程(7)所决定.G1(0,0),G2(y*,z*)的稳定性是由M的特征值的绝对值是否小于1决定. (i)若(1-d)ea2τ<1,即1-(1-d)ea2τ>0,G1(0,0)是唯一的不动点,则有 (8) (ii)若(1-d)ea2τ>1,即(1-d)ea2τ-1>0,G1(0,0)是不稳定的,且G2(y*,z*)存在,那么 (9) 显然M的特征根绝对值均小于1,由Jury判断准则,G2(y*,z*)是局部渐近稳定的.证毕. 引理3 (i)如果(1-d)ea2τ<1,那么系统(3)的平凡周期解(0,0)是全局渐近稳定的; (10) 其中y*和z*由式(6)给出. 定理2 (i)若(1-d)ea2τ>1,那么系统(2)的平凡周期解(0,0,0)是不稳定的. (ii)若(1-d)ea2τ>1,且 因此可得基解矩阵 这里(*)的准确形式是不需要计算的.系统(2)第四、五、六方程的形式如下: 系统(2)的第七、八、九方程的形式如下: 所以 λ2=e-d1τ<1, i) 由定理的条件i)以及Floquet定理,可知平凡周期解(0,0,0)不是稳定的. 下面证明全局吸引.任取ε>0,使得 (11) 由系统(2)的第二个方程,注意到 所以 (12) 由脉冲微分方程的比较定理,有y(t)≥y1(t),z(t)≥z1(t),且当t→时,即: (13) 对任意t>0,由式(2)和式(13),有 (14) 所以 x(nτ+)≤x((n-1)τ+)(1+ 因此x((n+l)τ+)≤x((n-2+l)τ+)ρ2≤…≤x(lτ+)ρn,所以当n→时,x((n+l)τ+)→0,那么当(n-1)τ 下面将要证明当t→时,若则一定存在一个t0>0,当任意t>t0时,使得0 (15) 这时,有w1(t)≤y(t)≤m1(t),w2(t)≤z(t)≤m2(t).当t→时,这里(w1(t),w2(t))和(m1(t),m2(t))是分别是下面方程的解: (16) 和 (17) 方程(17)的周期解为: (18) 其中 (19) 所以当(1-d)ea2τ>1和 下面证明系统(2)的持久性,在证明之前,给出如下定义: 定义2 若存在常数m,M>0(与初始值无关)和一个有限时间T0,使得任意t≥T0,对于满足初始值x(0+)>0,y(0+)>0,z(0+)>0的所有解均有m≤x(t)≤M,m≤y(t)≤M,m≤z(t)≤M,那么系统(2)具有持久性,这里T0取决于初始值(x(0+),y(0+),z(0+)). 定理3 若(1-d)ea2τ>1,且 那么系统(2)是持久性的,这里y*如式(6)所定义的. 1) 由定理2,选取m3>0,ε1>0且足够小,使得0 σ=a1τ-b1m3τ-βε1τ- 下面将证明,当t≥0时,x(t) (20) 由引理可知,y(t)≤g1(t),z(t)≤g2(t),且当t→时这里(g1(t),g2(t))是如下方程的解: (21) 可以得到系统(21)的解如下 (22) 这里(n-1)τ (23) 因此,存在一个T1>0,使得 (24) 且 (25) 当t>T1时,若N1τ>T1且n>N1,结合式(14),在区间((n-1+l)τ,(n+l)τ)上,有 x((n+l)τ)≥x((n+l-1)τ)(1+ x((n+l-1)τ)(1+p)eσ, 这时,x((N1+l-1)τ)≥x((N1+l)τ)ekσ→,k→,那么这与x(t)有界矛盾.因此,存在t1>0使得x(t)≥m3. 情况1t*=(n+l-1)τ,n1∈Z+,那么x(t)≥m3,对于t∈[t1,t*)且x(t*)=m3,x(t*+)=t*≥m3,选取n2,n3∈N,那么 en3gmaen2σ1τ>en3σe(n2+1)σ1τ>1, 这里 σ1=a1-b1m3-βM<0. 令T=n1τ+n2τ,那么一定存在某个t2∈[t*,t*+T]使x(t2)>m3,否则,考虑式 (14),g1(t*+)=y(t*+),有 t∈((n-1)τ,(n-1+l)τ], (26) 且n1+1≤n≤n2+n3,那么 系统(2)的第一个方程如下 (27) 结合式(26)在[t*,t*+n2τ]上,有 x(t*+n2τ)≥m3eσ1n2τ. 讨论了在两个斑块之间的三维捕食系统与脉冲入侵的种群动力学模型,证明了系统(2)解的正性、有界性,得到了边界周期解的全局稳定性的条件,结论表明外来物种成功入侵、本地物种趋于灭绝;由定理3可知,系统(2)在满足一定的条件下种群具有持久性,外来物种与本地物种共存.因此,物种迁移和食饵投放的间隔周期、迁移量和投放量均对系统的稳定性产生影响,进而在对相关物种进行管理时,需要选择相应的管理策略.
2 系统解的正性、有界性
3 子系统周期解的存在性和稳定性
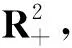

4 边界周期解的存在性与稳定性

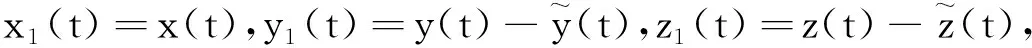

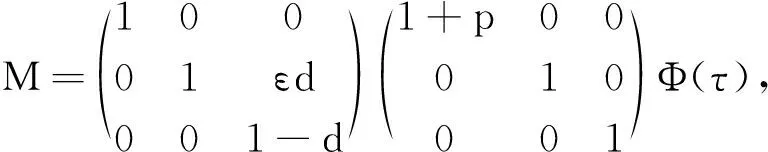
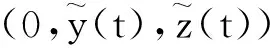

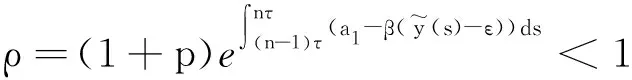
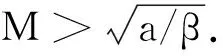


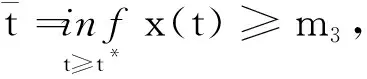




5 结束语

