Grothendieck范畴的斜群范畴

周振强

(厦门理工学院应用数学学院，福建 厦门)

1 预备知识

为了以统一方式研究模范畴和层范畴的同调理论,Grothendieck[1]于1957 年引入Grothendieck范畴.之后,Gabriel[2]进一步发展了该类范畴的相关理论.一个余完备的阿贝尔范畴称为一个Grothendieck范畴,如果 C 满足以下两条性质:

1) 任意短正合列的正向极限仍是短正合列.

2) C 具有一个生成子W,即函子 HomC(W,-) 是忠实的.由于 C 具有直和,该条件等价于：对 C 中的任意对象X,存在一个满态射W(I)→X,其中W(I)是对象W关于指标集I的直和.

(分次)模范畴、预层范畴、拟凝聚层范畴、函子范畴等诸多大家关注的范畴皆是Grothendieck范畴.

斜群范畴是斜群代数模范畴的推广.由Reiten等[3]在研究斜群代数的表示理论时首先引入.粗略地说,斜群范畴是由一个有限群G作用在一个预加范畴 C 上构造出来的新范畴.它的对象是范畴 C 中对象X的在群作用下的轨道的直和项.Reiten等[3]指出:研究范畴C 和斜群范畴 C(G)之间的联系不仅本身具有研究意义,而且从范畴的角度来看,应用斜群范畴这一工具,可使处理模范畴时,思路和脉络更为清晰直观.

本文中遵照文献[3]对斜群范畴的定义.设 C 是一个加法范畴,G是有限群.群G对范畴 C 的一个作用是指一个从G到 C 的自同构群Aut(C) 的群同态.记元素g∈G对对象X的作用为gX,g对态射β：X→Y的作用为gβ.若加法范畴 C 配备了一个有限群G-作用,则称 C 为G-加法范畴.若阿贝尔范畴 C 配备了一个有限群G-作用,则称 C 为G-阿贝尔范畴.

定义1设 C 是G-加法范畴,按如下方式定义范畴 C 的轨道范畴 C[G].C[G] 的对象为 C 中的对象.对任意对象X,Y∈C[G],定义态射集

态射的合成为自然的合成.

Reiten等在文献[3]中指出：若有限群G作用在一个幂等完备范畴 C 上,轨道范畴 C[G]未必是幂等完备的.为此,文献[3]引入如下定义.

定义2设G是一个有限群,C 是一个G-预加范畴.定义 C 的斜群范畴为轨道范畴 C[G] 的幂等完备化C[G],简记为 C(G).

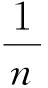
注1若去掉群的阶数的可逆性条件,则斜群范畴的性质都可能发生改变[4].

从现在开始,设定G是一个有限群,C 是一个G-阿贝尔范畴.记有限群G={e=g1,g2,…,gn}.则范畴 C 和 C(G) 之间存在两个重要的函子F：C → C(G) 和H：C(G) → C.

先在范畴 C 和轨道范畴 C[G] 上定义.对任意对象X∈C,定义F(X)=X.对任意 C 中的态射β：X→Y,定义F(β)：X→Y为 C[G] 中的态射

其中φe=β,对非幺元的元素g∈G,定义φg=0.

g1N⨁…⨁gnN,

ηX=(1X,0,…,0)T：X→HF(X)=

g1X⨁…⨁gnX,

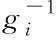
(εN)gi=(0,…,0,1N,0,…,0)：gi(g1N⨁…⨁gnN) →N.

其中第i个分支态射为第i个嵌入态射：

(ηM)gi=(0,…,0,1Mgi,0,…,0)t：giM→

FH(M)=g1M⨁…⨁gnM.

余单位ε：HF→ 1C在对象Y∈C 处的取值εY为

εY=(1Y,0,…,0)：g1Y⨁…⨁gnY=

HF(Y) →Y.

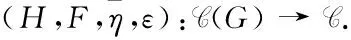
这里,仍采用原来 C 和轨道范畴 C[G] 范畴间函子和自然变换的记号.在不致混淆的情况下,将上述伴随对简记为 (F,H) 和 (H,F).文献[3]给出如下结果.

命题1设G是一个有限群,C 是一个G-阿贝尔范畴,且群G的阶数|G|=n可逆.则

3) 设X∈C,则HF(X)=⨁g∈GgX.设β：X→Y是 C 中的态射,则HF(β)：⨁g∈GgX→ ⨁h∈GhY是主对角线为gβ：gX→gY,其余位置为零态射的n阶态射矩阵.

2 定理和推论

命题2[4]设G是一个有限群,C 是一个G-阿贝尔范畴,且群G的阶数可逆.则斜群范畴 C(G) 是一个阿贝尔范畴.进一步地,(F,H) 和 (H,F) 是阿贝尔范畴间的正合函子的伴随对,从而函子F和H皆保持极限和余极限.

引理1[5]设G是一个有限群,C 是一个G-阿贝尔范畴,且有限群G的阶数在 C 中可逆.则下述命题成立.

1) 设X,Y∈C.则 C 中的态射β：X→Y是单的 (或满的),当且仅当 C(G) 中的态射F(β)：F(X) →F(Y) 是单的(或满的).

定理1设G是一个有限群,C 是一个G-阿贝尔范畴,且有限群G的阶数在 C 中可逆.若 C 是一个Grothendieck范畴,则斜群范畴 C(G) 是一个Grothendieck范畴.

证明由命题2可知,只需证明斜群范畴 C(G) 是余完备的,正向极限是正合函子,且具有一个生成子.

首先证明 C(G) 的余完备性,即证明 C(G) 具有任意的余极限.由于 C(G) 是阿贝尔范畴,其余核存在.这当且仅当证明 C(G) 具有无限直和.设 {Mi}i∈I是 C(G) 中以I为指标集的任意对象族.则{H(Mi)}i∈I是 C 中的一族对象.由C的余完备性可知,其直和存在,记为C=⨁i∈IH(Mi).由F保持直和 (命题2),从而F(C)=⨁i∈IFH(Mi) 是对象族{FH(Mi)}i∈I在 C(G) 中的直和.

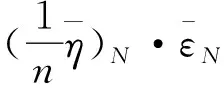
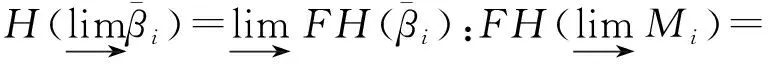
最后证明 C(G) 具有生成子.设 C 的生成子为W,则 HomC(W,-) 是忠实函子.由正合伴随对 (F,H) 立即可知函子 HomC(G)(F(W),-)≃HomC(G)(W,H(-)) 的忠实性.这便说明对象F(W) 是范畴 C(G) 的生成子.

推论1设G是一个有限群,C 是一个G-局部有限生成范畴,且有限群G的阶数在 C 中可逆.则斜群范畴 C(G) 是一个局部有限生成范畴.

证明设 {Xi}i∈I是 C 中的一族有限生成的生成子.类似定理1的证明可知 {F(Xi)}i∈I是 C(G) 中的一族生成子.下面证明它们是有限生成的.

设 {Ni}i∈I是 C(G) 中对象N的任意正向子对象族.由 C(G) 是Grothendieck范畴 (定理1),知 C(G) 的正向极限存在,则有

利用正合伴随对 (F,H) 以及函子H保持正向极限,得

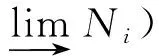
此即证明斜群范畴 C(G) 是一个局部有限生成范畴.

如果对象X的子对象族满足 Noether 条件,则称X是 C 中的 Noether 对象.如果一个Grothendieck范畴 C 具有一族 Noether 生成子,则称 C 为局部 Noether 范畴.局部 Noether 范畴是常见的.设R是环.则右模范畴Mod(R) 是局部有限生成范畴.进一步地,Mod(R) 是局部Noether范畴当且仅当R是右Noether环,参见文献[6]第Ⅴ章.

推论2设G是一个有限群,C 是一个G-局部Noether范畴,且有限群G的阶数在 C 中可逆,则斜群范畴 C(G) 是一个局部Noether范畴.

证明设 {Xi}i∈I是 C 中的一族Noether生成子.则 {F(Xi)}i∈I是 C(G) 中的一族生成子.下面证明它们是Noether 的.在Grothendieck范畴中,对象X是Noether的,当且仅当X的子对象是有限生成,参见文献[6]第Ⅴ章命题 4.1.故等价于证明F(Xi) 的每一个子对象是有限生成的.设M是F(Xi) 的任意子对象.由函子H保持单射 (引理 1),知H(M) 是HF(Xi) 的子对象.由命题1知,HF(Xi)=⨁g∈GgXi.立即地,对每一个g∈G,gXi是 C 中的Noether对象.据文献[6]中第 V 章命题 4.2 知,Noether对象的直和HF(Xi)=⨁g∈GgXi仍是Noether的.故子对象H(M) 是有限生成的,由推论1的证明知,F保持有限生成对象.从而有限生成对象FH(M) 的直和项M是有限生成的.此即证明斜群范畴 C(G) 是一个局部 Noether范畴.

设 C 是一个Grothendieck范畴.称X是 C 中的有限表现对象,如果 HomC(X,-) 保持正向极限.若一个Grothendieck范畴 C 具有一族有限表现的生成子,则称 C 为局部有限表现范畴[7].类似推论1的证明可得如下结果.

推论3设G是一个有限群,C 是一个G-局部有限表现范畴,且有限群G的阶数在 C 中可逆.则斜群范畴 C(G) 是一个局部有限表现范畴.