多自由度空间摆动式自动喷洒机构设计与实现

沈林鹏，涂福泉，李 根，李 恒，刘谋泽，刘浩杰

(武汉科技大学 机械自动化学院，武汉 430081)

0 引言

在完成对农作物及树木花草的喷洒作业的过程中，往往伴随着作业环境恶劣、喷洒高度不够及喷洒效率低等诸多原因的限制。往复式自动喷洒机构的设计研制实现了自动喷洒，而喷洒的均匀性成为研究的核心。考虑到喷洒机构在工作过程中，存在摆动导杆与滑动套管之间的摩擦力会造成喷洒机构的寿命降低，两者的相互摩擦力也成为研究核心。针对于喷头喷洒性能，国内外学者进行了大量研究。陈超等[1]研究了异形喷嘴对变量喷头水量分布的影响，星形喷嘴变量喷头的水量分布均匀度好于圆形喷嘴变量喷头,方形喷洒域的均匀度好于三角形喷洒域。张慧春等[2]利用开路式风洞系统和Sympatec激光粒度仪测试了参考喷头的雾谱尺寸，对扇形雾喷头在不同压力、风速、喷头与激光粒度仪距离情况下的雾滴粒径、数量和范围进行了试验，得出了压力、风速、喷头与激光粒度仪之间距离的增大，对喷头的喷洒性能都存在影响。Hislop E C[3]等研究了喷头的安装高度、角度及风向与风量的大小对喷洒效果及均匀性的影响。张波等[4]针对目前运煤列车防冻液喷洒装置不能升降且在停止喷洒时喷头中残液滴漏等问题，设计了一种多功能式防冻液喷洒装置。顾文杰[5]等设计了适合中小田块的六旋翼农药喷洒无人机。以上对影响喷头喷洒性能的因素进行的研究及设计的喷洒装置均存在使用条件的限制，并未涉及对果树、农作物与城市街道绿化的树木花草自动喷洒装置的设计与研究。

本文针对于农作物与树木花草进行喷洒药物时的农艺特点，设计了一种农用喷洒车多自由度空间摆动式自动喷洒机构，并根据初始设计参数，通过对喷洒机构建立ADAMS虚拟样机模型，进行运动学分析。以影响喷洒均匀性、稳定性为优化目标函数，以摆动导杆与套筒之间相互作用力为优化目标函数，机构设计尺寸参数为设计变量，建立Adams虚拟样机优化模型，经过迭代求解，最终求得最优化设计参数，以期达到能够理想地完成自动喷洒作业。

1 多自由度空间摆动式自动喷洒机构的运动学分析

1.1 工作原理

往复摆动式自动喷洒机构主要由电机、曲柄、摆杆喷头、滑块、可调支架及底座组成，如图1所示。

其机构原理图如图2所示。由图2可以看出：对于整个机构而言，LAE与LDE为整个机构系统固有的结构参数，在设计时必须要合理的选取LAE与LDE的尺寸参数。除此之外，对整个机构运动特性存在关键影响的是电动推杆BC与电机的驱动函数。然而，对于整个机构系统设计而言，机构固有尺寸参数的最优化确定是整个系统确定的首要关键问题，对于整个机构系统的驱动部分，因为柔性度较强，可以在完成整个机构系统之后采用调试的方式对于驱动部分进行选取。

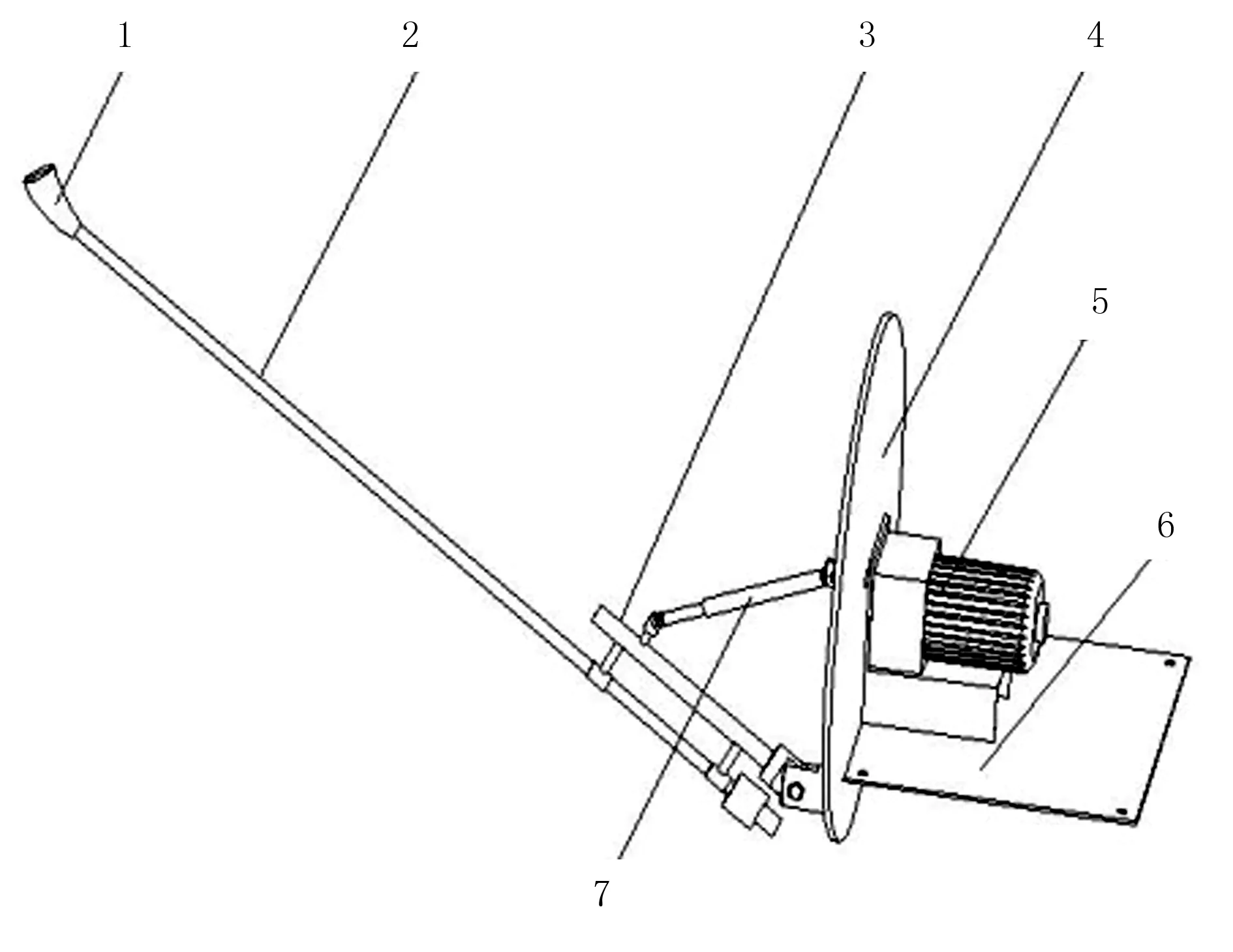
1.高压喷头 2.喷杆 3.喷杆支架 4.圆形转盘 5.电机 6.底座 7.电动撑杆图1 往复摆动式自动喷洒机构

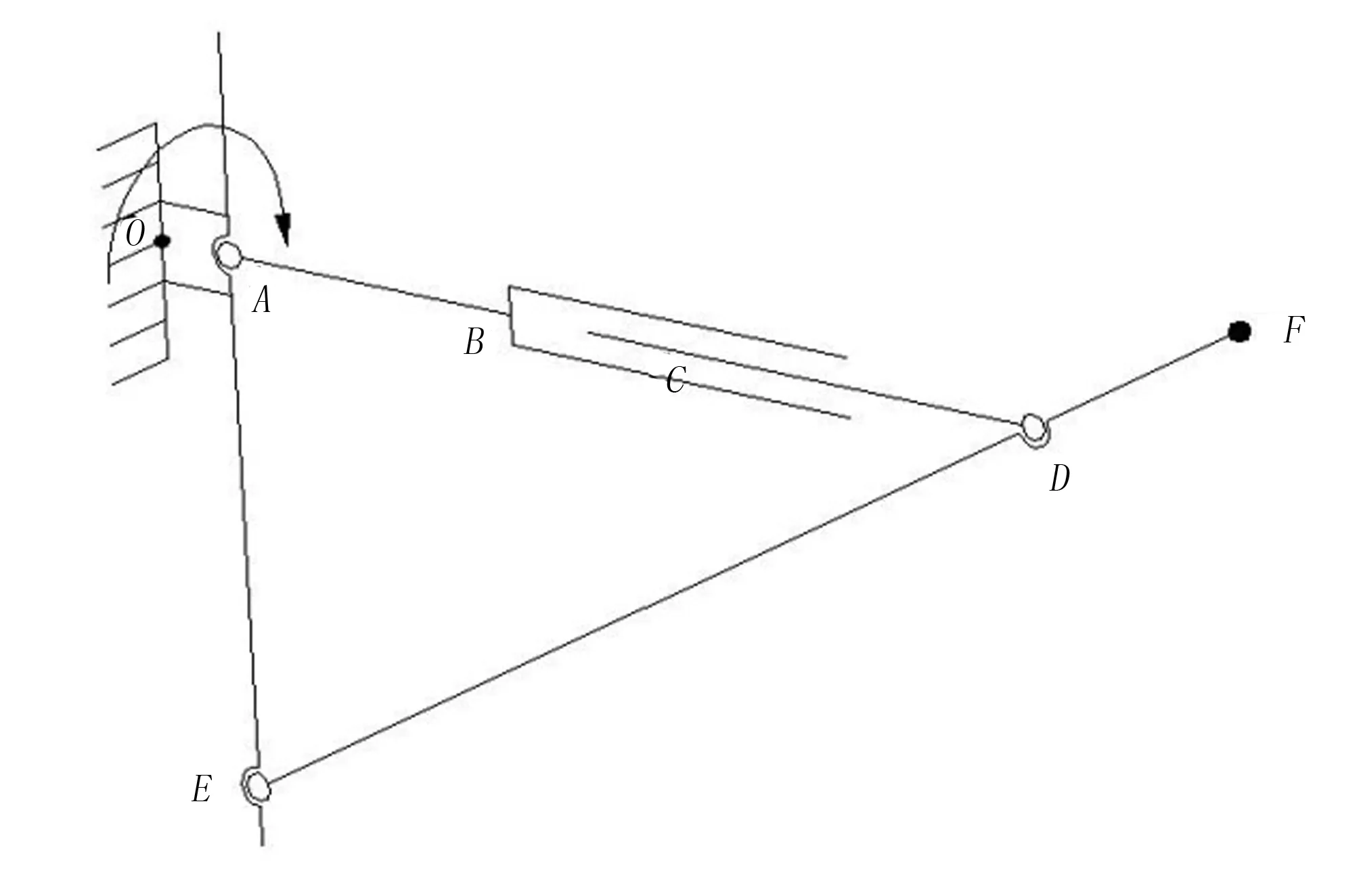
图2 喷洒机构原理图

1.2 初始参数的确定

选取电动撑杆最大有效行程为300mm，即200mm≤LAD≤500mm，取LAD=400mm；LAE=300mm；LED=500mm。其结构尺寸图如图3所示。

图3 初始结构尺寸图

1.2.1 建立机构仿真模型

根据往复摆杆式喷洒机构的运动原理与机构的设计要求设定了各机构参数，从而确定其关键坐标点，如表1所示。根据创建的关键点，建立机构的虚拟样机模型如图4所示；按照机构实际连接约束，对各实体link施加 revolution约束如表2所示。

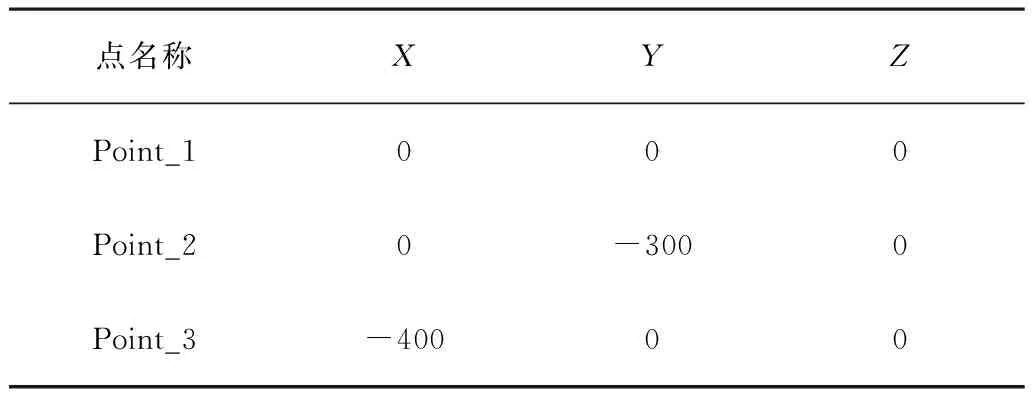
表1 各关键设计点坐标

图4 多自由度空间摆动式自动喷洒机构虚拟样机模型表2 多自由度空间摆动式自动喷洒装置机构的运动模型约束表

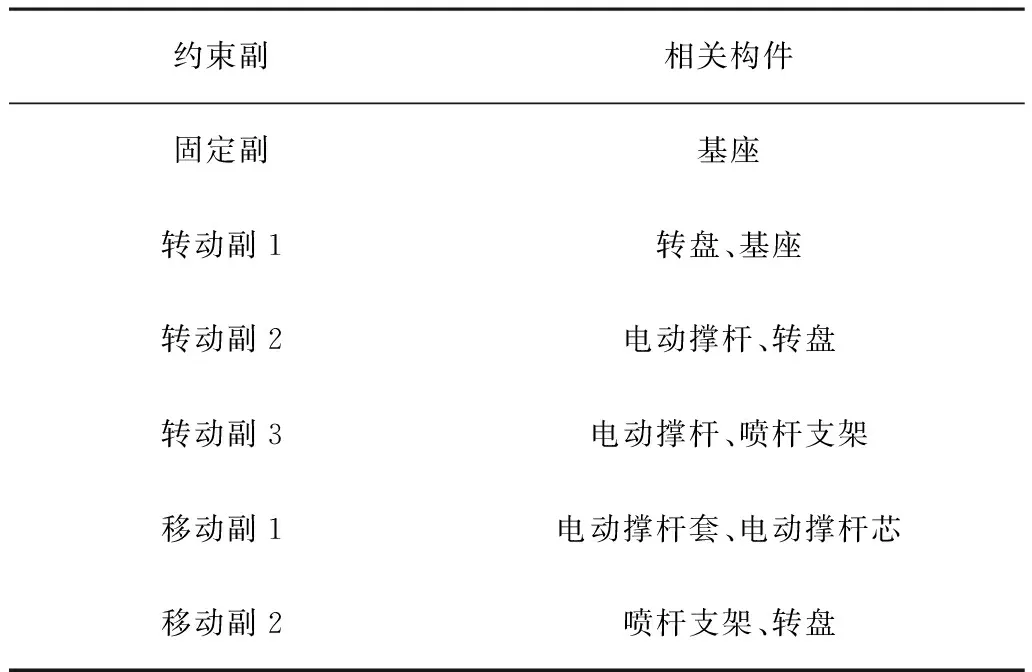
约束副相关构件固定副基座转动副1转盘、基座转动副2电动撑杆、转盘转动副3电动撑杆、喷杆支架移动副1电动撑杆套、电动撑杆芯移动副2喷杆支架、转盘

对空间喷洒装置的结构进行简化，用连杆来代替装置各部件，使得仿真图的各杆的质心、惯性矩等参数就会与实际的不符，最终得到的运动学和动力学分析也与实际的不同。因此，仿真图形在形状上简化为好，而各参量必须与实际相符。这样在仿真造型之前，需要计算各杆件的质量、质心位置和惯性矩、惯性积[6]。

各杆件的质量公式为

m=ρ·V

各杆件的质心公式为

各杆件的惯性矩和惯性积的公式为

Jxx=∑mi·(yic2+zic2)Jxy=∑mi·xic·yic

式中xc、yc、zc—杆件的质心坐标；

mi—杆件中的第i个零件的质量；

xic、yic、zic—第i个零件的重心坐标。

根据以上公式计算出各杆件具体的质量、质心和惯性矩、惯性积的值。

根据傅里叶变换得，任何函数都可以经过傅里叶变换转换为正弦或余弦函数。考虑到喷洒工艺特点，初步设定转盘主轴的角位移为1.5·cos(0.1·time)，电动推杆的直线运动位移函数为35·cos(0.1·time)。

1.2.2 机构运动学仿真分析

以摆杆为研究对象，通过对机构进行仿真，得出摆杆的位移、速度和加速度曲线如图5所示。

图5 喷洒机构导杆质心运动曲线

由图5可知：曲柄在转动1周的过程中，该机构经历了1个周期，喷杆的速度经历了两次波峰和一次波谷，分别代表摆动导杆经历了加速-减速-加速的过程。当t=11.5 s与t=10.5 s时速度达到最大，v=12mm/s，说明此时喷杆速度达到最快；当t=31.5 s时减速至最小，v=0，说明此时喷杆运动至极限位置，杆机构出现急回特性，摆动导杆出现抖动，这对机构的稳性有较大的影响。

从加速度曲线变化上来看：在喷杆运动1个周期的过程中，加速度经历了两次波峰与一次波谷，当t=31.5s时减速至最小，v=0，此时对应加速度最小，其分别对应摆动导杆运动至极限位置。加速度由最大变化至最小，再变化至最大，这两个过程中加速度表现出剧烈变化，摆动导杆发生抖动。

2 参数优化分析

2.1 建立参数化模型

当喷洒机构在运行的过程中，为了使喷洒更加均匀，要求导杆在摆动时，应尽可能保持匀速。将ADAMS参数优化设计方法用于优化摆动导杆机构的速度稳定性，将运动点的坐标作为设计变量，并对坐标值进行参数化，建立摆动机构的参数化模型，进而对每个设计变量的灵敏度分析计算，从而找出关键设计变量，并在优化计算中确定每个关键设计变量的最优参数，最终得出速度平稳性最优的摆动导杆机构的尺寸参数[6-10]。摆动导杆机构简图如图6所示。

图6 喷洒机构优化仿真模型

在往复摆动喷洒装置喷洒运动导杆机构中，模型元素主要是几何点，用点的坐标变化表示杆长变化，因此需要完成点位置的参数化。改变各个参数点的位置是通过改变坐标值的方式来完成，达到改变杆长条件[11]，得到参数化后的结果如表3所示。

表3 参数化结果

2.2 对参数化设计变量进行优化

确定参数设计变量后，可优化关键设计变量。使用Adams的参数优化的一个明显优点是可以将被测量用作优化度量的目标函数。在往复摆动喷洒装置喷洒运动导杆机构模型中，为了获得准确的速度平稳性，以垂直于导杆轴向的方向的加速度变化为测量指标，将速度、加速度共同作为观测依据，将垂直于导杆轴向的方向的速度、加速度的平均值作为优化目标，得到参数化优化结果如图7～图10所示。

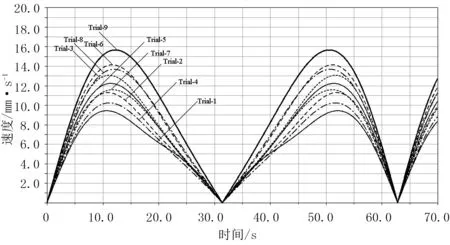
图7 自动喷洒机构导杆速度迭代优化曲线

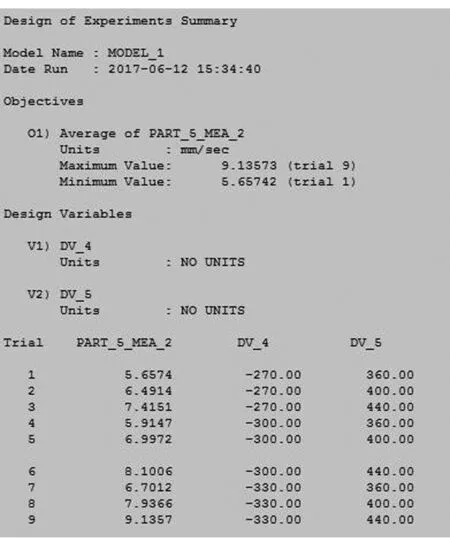
图8 喷洒机构导杆速度迭代优化报告表

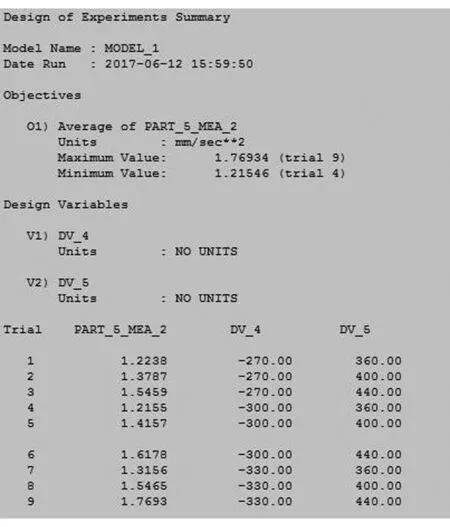
图10 喷洒机构导杆加速度迭代优化报告表

由图7与图9中可以看出：经过迭代优化之后，往复摆动喷洒装置喷洒运动导杆机构在做往复摆动时，整个周期运动特性明显呈现平稳态势。从喷杆速度迭代优化曲线可以看出：Trial 1模式下，喷杆的速度变化显著变缓，有利于机构喷洒的均匀性；但此模式下，在t=14～32s与t=32～50s期间，速度的变化表现出非线性变化显著，说明其速度不稳定。Trial 4模式下，喷杆速度的变化与Trial 1接近，在t=14～32s与t=32～50s期间，速度的变化表现出线性变化，说明其速度稳定。因此，从速度稳定性方面考虑，Trial 4模式要优于Trial 1模式。从摆杆加速度迭代优化曲线可以看出：Trial 4模式下，摆动导杆的加速度变化显著变缓，对整个机构的冲击明显变小，抖动明显变小。

综上仿真分析可以得出：当转盘与喷杆连接点与转盘中心的距离L1=300mm、电动撑杆芯接头与喷杆的连接点位于喷杆杆身与喷杆尾部之间的距离L2=468.6mm时，对于整个机构而言，其喷洒均匀性最好，摆动导杆抖动最小。

3 试验与分析

3.1 试验样机的建立及试验条件

根据优化求解得到的最优尺寸参数为设计依据，对试验样机装置加工制作，搭建装配得到如图11所示的试验样机装置。

1.电机 2.电机固定底座 3.移动支架 4.固定支架 5.喷杆固定套管 6.水箱 7.软管 8.电动撑杆套 9.电动撑杆芯 10.圆形转盘图11 样机试验模型

喷洒机构的运动学试验主要是利用加速度传感器测量，主要是测量喷杆的加速度特性。试验装置输出端添加一个积分环节，测量摆杆的速度特性。图12为加速度传感器。加速度传感器主要是靠粘接剂粘贴于喷杆端部，测量喷杆头部的运动特性。

图12 压阻式加速度传感器

3.2 试验结果分析

经过试验得出喷杆的速度曲线与加速度曲线，如图13和图14所示。

由速度变化曲线可以看出，喷杆速度的变化明显变缓，波峰最大值小，喷杆运动抖动变小；由加速度变化曲线可以看出，喷杆加速度的变化明显变缓，波峰最大值小，喷杆运动冲击变小，喷洒均匀，喷洒效果好。

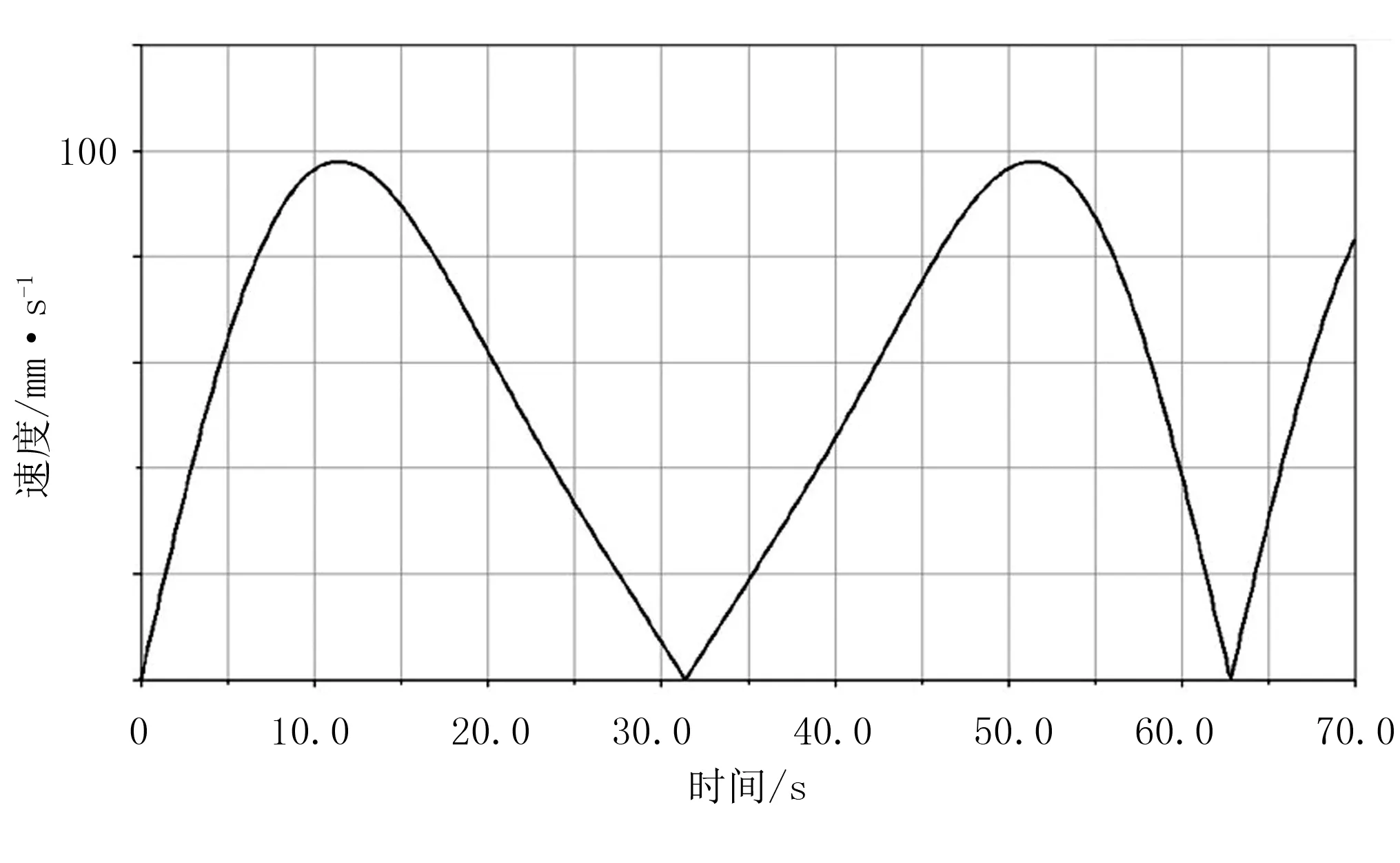
图13 试验测量喷杆速度曲线

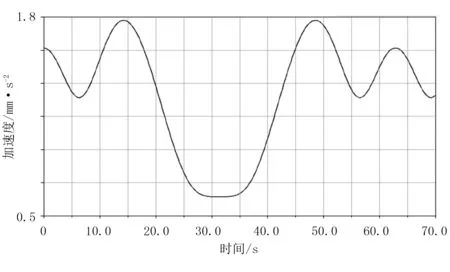
图14 试验测量喷杆加速度曲线

4 结论

1)利用Adams软件对该机构进行动力学虚拟建模仿真试验，通过设置虚拟仿真参数，模拟喷洒机构运动情况，分析喷洒机构在喷洒过程中的位移-速度-加速度情况，为设计提供理论指导。

2)对喷洒机构进行了初步设计，在此基础上寻求最优化参数，经过迭代优化之后，求得的最优化值，进一步对该机构的设计提供了理论依据。

3)利用迭代优化求得的机构最优化参数，建立往复摆动导杆式自动喷洒机构试验样机进行喷洒试验，试验结果均满足实际应用要求。