油菜联合收获机结构参数对割台振动的影响

任述光，焦 飞，吴明亮，何顺舟，唐升仲

(1.湖南农业大学 工学院，长沙 410128；2.湖南省现代农业装备工程技术研究中心，长沙 410128；3.南方粮油作物协同创新中心，长沙 410128)

0 引言

油菜收获损失是制约油菜收获机械化发展的重要因素，现有资料表明，油菜收获过程中，总损失平均为8.54%，其中割台损失为7.69%[1]，占收获损失的90%。割台振动是引起割台损失的主要原因[1-2]，是收获损失的最直接来源。目前，我国油菜收获机大多在谷物联合收获机的基础上改装而成，多采用往复式切割器。由于往复式切割器的割刀和驱动机构在工作时产生较大的惯性力，在内部惯性力激励和外部切割冲击力激励的共同作用，切割器及割台产生较大的振动，引起收获损失及零部件磨损，也影响机器的使用寿命和工作质量。为减小收获损失，提高收获效率，国内外一些学者进行了卓有成效的研究。李耀明等[1]对油菜收获机的割台损失影响因素进行了试验研究，提出减少拨禾轮对油菜打击次数，降低对果荚冲击力等措施。陈翠英、王新忠等[3]对谷物联合收获机割台设计进行了基础性的研究，提出了在未割边加装竖直切割器和改变拨禾轮参数的办法解决因分禾拉扯和拨禾轮打击而造成损失大的问题。为避免机器工作时产生共振，陈翠英[4]对4LYZ-2型油菜收获机台框架进行了有限元模态分析；为获得不同工况下切断油菜茎秆的切割力，吴明亮[5-8]进行了油菜茎秆切割力影响因素的试验研究，得到茎秆一些力学性能参数。孙书民、夏萍等[9-10]分别进行了切割机构的运动学与仿真分析，获得了切割器运动过程中的速度、加速度曲线；陈振玉[11]对往复式切割器切割过程的一次切割区、重割区以及漏剖区面积在不同切剖情况下的变化特性进行了理论分析，得出了相应的速度匹配参数。虽然国内有些学者提出用回转式圆盘切割器替代传统的往复摆动式切割器[12-13]，并进行了相应的尝试，但由于在技术上还不够成熟，该机型还未得到普及应用，往复式切割器仍是南方油菜收获的主流机型。研究切割系统的运动及动力学特性，分析引起割台振动的因素，了解割台系统的振动特性，研究割台对割刀惯性力及切割冲击力等激励的响应，对于设计优质高效的切割系统，提高机器的工作性能具有重大理论和实践意义。与国外相比，我国对联合收获机各种工况下的振动强度及整机抗振性能的研究仍处于起步阶段，对收获机底盘机架及割台的振动研究也比较少[14-17]；有些学者进行过切割系统动力学研究[18]，对割台振动模态进行了有限元方面的数值求解[5,17]。现有资料表明：割台振动方面理论研究还较为欠缺，值得进一步探索。

1 切割系统动力学分析

1.1 机构运动分析

收获机切割系统属于转向式曲柄连杆机构，由切割器、压刃器、拨禾轮、机架、平衡飞轮、连杆，以及三角摆块等零部件所组成。曲柄为平衡飞轮的一部分，动力经由液压马达输入使其绕定轴转动，从而通过连杆使三角摆块绕球铰链中心轴摆动，带动割刀做水平往复运动，完成切割任务。收获机割台切割器传动机构示意图如图1所示。其中，飞轮B绕轴A转动，对带动与之铰接的连杆BC运动，通过圆柱铰链C带动水平面内的三角摆块CDE绕球铰链D做小幅摆动，通过滑块E推动固定在导筒上的割刀F做往复运动，完成切割动作。建立空间坐标系OXYZ如图1(a)所示。将绕轴A转动的飞轮B视为曲柄，则在铅垂面XOZ中机构简化为偏置曲柄-连杆-滑块机构，如图1(b)所示。由于连杆长度远大于三角摆块的直角边长，为分析简单，可只考虑C点在X轴方向上的位移xC而忽略其Y轴方向上的位移。由于摆块CDE为等腰直角三角形，故滑块E沿y方向的位移yE=xC，割刀位移yF=yE，因此yF=xC。

图1 切割器传动机构示意图Fig.1 Sketch map of transmission gear of cutter bars bars

半径(曲柄长度)为r，角速度为ω，连杆长度为l，飞轮中心与滑块之间的铅垂距离(偏心距)为e，并令κ=e/l，λ=r/l。以曲柄旋转中心为坐标原点，曲柄与OX轴的夹角为θ=ωt，连杆与OX轴所夹锐角为φ，在ZOX坐标面中，割刀位置为

xC=rcosθ+lcosφ

(1)

由几何关系得

lsinφ=e+rsinθ

(2)

经运算可得

(3)

对式(3)求导，并将式(4)代入，得割刀速度为

(4)

考虑到λκ，加速度近似为

(5)

1.2 切割系统惯性激振力分析

设连杆质量为m0，以等效集中的方法[19]，把曲柄(飞轮)的质量集中到曲柄销B，连杆的质量集中到曲柄销B和割刀E，忽略三角摆块质量。运动部件的质量最后可用曲柄销的等效质量m1e和割刀的等效质量m2e来表示。连杆质心到端点B的距离b可由试验确定[20]，令k=b/l。将连杆视为位于曲柄销B及滑块C位置的两质点，可求得连杆等效到曲柄销和割刀的质量me为

(6)

其中，J为连杆绕质心轴的转动惯量(kg·m2)；K=1-2kcos2θ+k2cos2θ。

作用于曲柄销的惯性力即为连杆等效质量m1e的惯性力，其水平分力为

F1=m1erω2cosωt

其中，ω为曲柄角速度。可以通过在飞轮上增加配重的方法消除连杆等效到曲柄销的惯性力。连杆质量和传动机构偏心距情况e的不同，根据式(9)，由MatLab编程，计算出曲柄转动周期内连杆等效到曲柄销的最大质量[19-20]，也就是需在对称飞轮中心配置的平衡块质量。表1是连杆长度l=0.75m，k=0.5的情况下，计算得到的平衡块的质量。

表1 不同偏心距时的飞轮平衡配重Table 1 The flywheel balance weight of different eccentricity

割刀的惯性力为

(10)

其中，m2e=m2+me。

机构运动时的惯性力与连杆质心位置k值有关。在n=300r/min、e=0.4、m2=3kg、m0=2kg的情况下，绘曲柄转动周期内割刀惯性力变化曲线，如图2所示。由图2可知：当k=0.5时，即连杆质心位于杆的中心时，等效到割刀的最大惯性力最小，该值约为120N，为割刀重量的4倍。当连杆质心靠近割刀时，割刀最大惯性力增大，如k=0.87时，最大惯性力达170N。

图2 不同k值下割刀惯性力随曲柄位置变化曲线Fig.2 The curves of the cutter inertia force vs crank position under different k value

1.3 切割冲击力

割台水平方向的激振力除上述两部分外，还有割刀切割茎秆的切割力，切割力为

F3=nFsinαsin2ωt

其中，α为割刀半顶角；n为同时参与切割的刀齿数；F为切割力的幅值。

刀切割茎秆为剪切过程，切割力的幅值可近似由下式得到

F=Aτu

其中，A为茎秆横截面积(m2)；τu为茎剪切强度极限(N/m2)。

工作过程中，引起系统的激励为曲柄、割刀的等效惯性力及割刀切割冲击力之和，改进设计后，在带轮上进行了平衡配重，可以消除激振力F1。因此，激振力为割刀工作过程中的惯性力与切割冲击力之和，可表示为

(11)

图3 动刀片切割载荷示意图Fig.3 Sketch map of loading on knife section

2 割台振动微分方程及求解

为简单起见，只考虑平行于割刀方向的振动，将割台视为以一定的刚度系数和收获机底盘相连的单自由度弹性系统，并假设振动过程中受到粘性阻尼力，运动过程中的阻尼力与振动速度成正比。根据达朗贝尔原理建立割台水平方向振动微分方程为

(12)

其中，x为系统离开静平衡位置的位移(m)；m为割台系统的总质量(kg)；c为割台与收获机主体连接的刚度系数(N/m)；η为系统运动过程中的阻尼系数(kg/s)。将激振力式(11)改写为

方程(12)是二阶常系数非齐次线性微分方程，其齐次方程的通解为振幅按指数规律衰减的瞬态响应，在阻尼作用下，经过充分长的时间后瞬态振动趋于零[21-22]。式(13)表明，割台水平振动的激励频率有两个：ω和2ω，这两个不同频率的激振力会使系统产生两个相应频率为ω和2ω的稳态等幅振动。频率为ω的激振力由割刀运动惯性力引起；频率为2ω的激振力由两部分组成，一是由于割刀惯性引起的，另外一部分是由于切割阻力引起的。计算表明，割刀惯性力引起的激振力幅值较切割阻力引起的幅值小很多，因此为简化分析这部分激振力可以略去不计。此时式(13)可简化为

(14)

(15)

其中，ψ1、ψ2为振动初相位。两个不同激振频率下的放大率β1、β2分别为

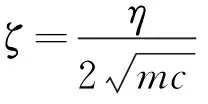
3 结构及工作参数对振动影响分析

根据式(14)绘出频率为ω的激振力在一个周期内变化曲线，如图4所示。可见，激振力的幅值也与偏心距e有关，偏心距越大，激振力的幅值越大。图4绘出了转速n=300r/min条件下，3个不同偏心距时激振力在一个周期内的变化情形。偏心距e=0.3时，激振力的幅值为130N；偏心距e=0.4时，该值增大到138N；当e=0.5时，该值增大到150N。因此，为使激振力的幅值不至过大，设计时偏心距不宜过大。

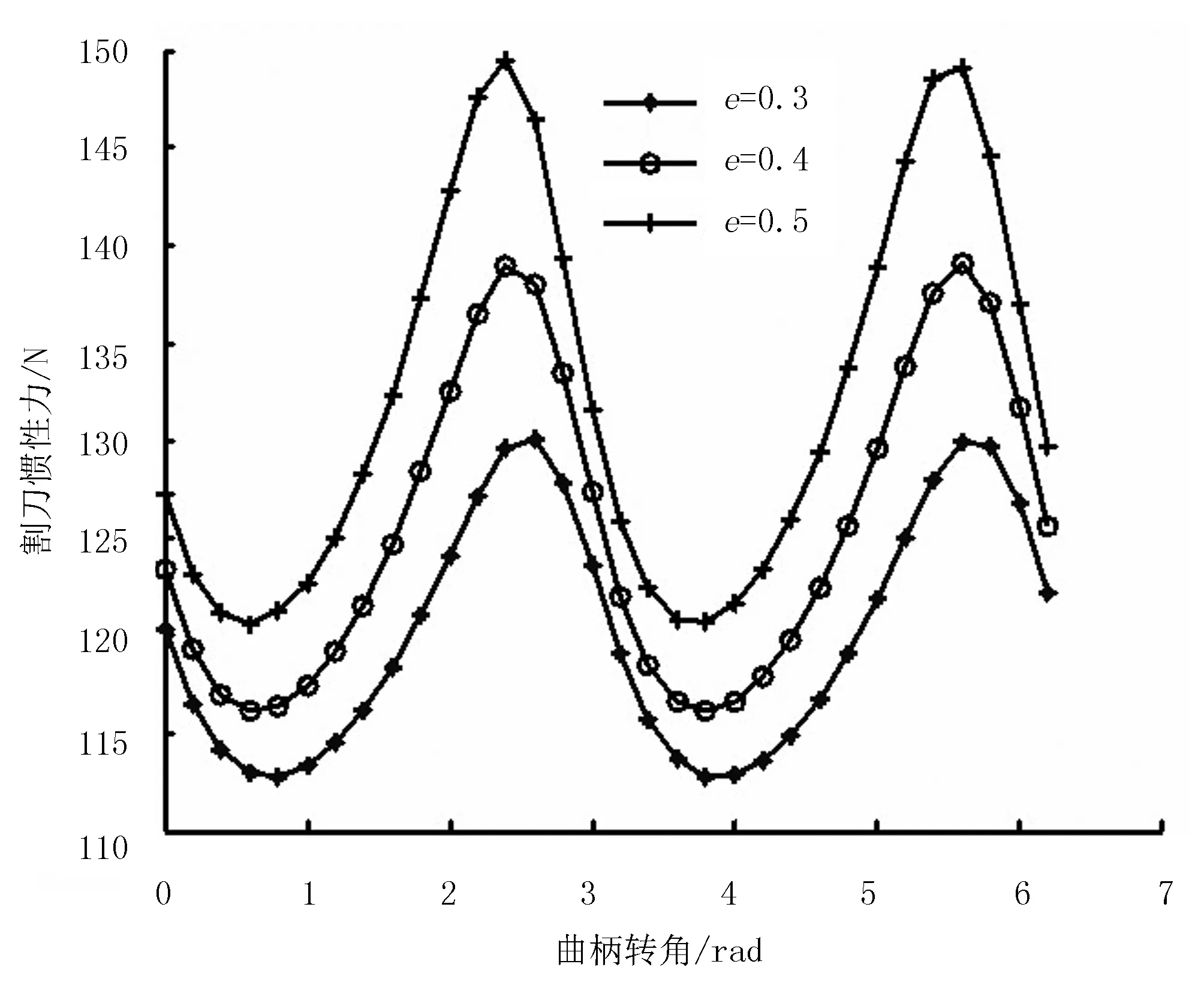
图4 不同e值下割刀惯性力随曲柄位置变化曲线Fig.4 The curves of the cutter inertia force vs the crank position

以激振频率与固有频率的比值γ为横坐标，振幅放大率β为纵坐标，绘出不同阻尼比时的幅频特性曲线，如图5所示。由图5可知，在相同频率比下，阻尼越大，放大率越小。

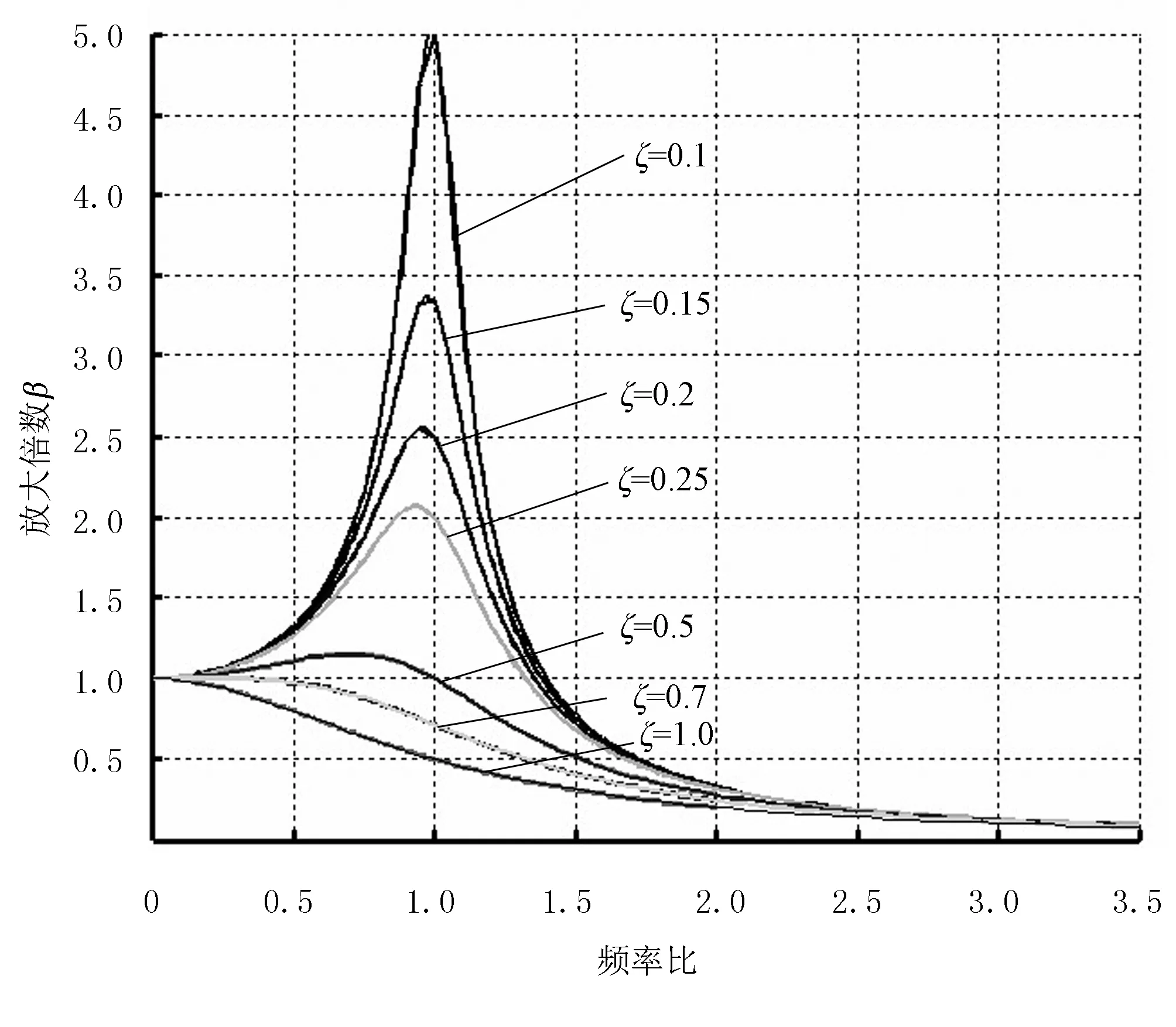
图5 不同阻尼下割台系统的幅频特性曲线Fig.5 The amplitude-frequency characteristic curve of cuttingTable under different damping

正常工作时，曲柄转速在300～500r/min之间，其固有频率范围在20.2～20.7Hz之间。频率为ω的激振频率与一阶固有频率的比值0.20≤γ≤0.40，离共振频率比γ=1较远；频率为2ω的激振频率与1阶固有频率的比值0.40≤γ≤0.80，工作过程中不会出现割台共振现象，但为了使振幅不致过大，曲柄转速以不超过500r/min为宜。由幅频特性曲线可知，在系统固有频率一定的情况下，随激振频率的提高，振幅放大率增大。频率为ω的激振频率引起振幅放大率，频率为2ω的激振频率引起振幅放大率1.3≤β≤1.4。这两个激振频率相比较，高频激励引起的振幅放大率较大，引起割台振动的高频激振频率来源于机构运动过程中的惯性力和茎秆切割过程中的冲击力。当激振频率与固有频率的比值γ>1，由幅频特性曲线可知，随频率比γ增大，振幅放大率下降，稳态响应的幅值反而减小。这种情形下，振幅主要取决于系统的惯性质量。γ>2时，阻尼对稳态响应的幅值影响很小，利用阻尼减小振幅不可取。

4 试验

根据以上理论分析的结果，将联合收获机割刀、割台及切割传动部件进行改进，改装割台，在飞轮上进行配重，并尽量使连杆质心向靠近飞轮曲柄销方向移动。2016年5月，在浏阳县北盛镇的油菜基地现场收获时进行了改进前后机器工作时振动测试试验。试验采用TV300便携式测振仪，技术性能参数为：加速度峰值范围0.1～392m/s2，速度有效值范围0.01～80cm/s，频率范围10～1kHz，位移峰值范围0.001～18.1mm，频率范围10～500Hz。试验前将磁性吸座下边的铁片和橡胶垫取下(保证有足够的吸力)，将TSV-01测振探头与割台连接牢固，接触紧密，确保测振探头主灵敏轴位于水平方向；然后再将测振探头TSV-01与仪器相连，调节飞轮转速，测量转速为300、350、400、450r/min的工况下振动参数，试验前先根据激振频率选择频带范围，测量完成后，切换显示方式为“专用型”，记录振幅、速度、加速度，结果如表2所示。

表2 改进前后不同转速条件下振动参数试验结果

Table 2 Vibration parameters contrast before and after improvement under the conditions of different speed

皮带轮转速/r·min-1振幅/mm改进前改进后速度有效值/mm·s-1改进前改进后加速度幅值/mm·s-2 改进前改进后3000.180.162.982.65178.24158.103500.210.194.173.77290.02262.404000.250.225.514.85438.57385.804500.290.267.196.45643.86577.21

5 结论

1)可以通过在飞轮上增加平衡配重消除部分惯性力，以减小机器的振动，提高作业质量。配重大小可由分析结果编程计算得到。连杆等效到割刀的惯性力无法消除，为引起系统振动的振源之一，为减小这部分激振力，设计时尽量使连杆质心远离割刀端的销轴。

2)虽然增大阻尼能起到抑制振幅的作用，但实际工作中，阻尼过大，机器消耗的功率也会增大。在许可的条件下，尽量减小割刀的质量，以减小割刀工作过程中的惯性力。通过本文计算结果改进设计后，可使振幅减少11%。

3)引起系统振动的两个激振频率ω和2ω，由于后一频率较前一接近系统固有频率，故其对系统振动起主要作用。机器设计时应考虑飞轮转速，避免工作过程中出现振幅过大的情况。

4)在2ω的激振频率中，割刀的切割阻力对振幅起主要作用，切割阻力取决于收割时茎秆的力学特性，主要与茎秆成熟度与含水率有关，因此油菜收获时机也是收获过程中需要考虑的重要因素。

5)本文忽略了传动系统的惯性力激励引起的铅垂方向的振动。割台实际振动应该是水平与铅垂两个方向振动的合成，但由于其铅垂振动较水平振动小很多，本文的简化是可行的。