电励磁同步电机系统及直流电压容错控制研究
刘 娜,肖 柱,王宁宁,陶梦江
(1.中国矿业大学,徐州 221008;2.国网淮南供电公司,合肥 230061;3.国网安徽省电力公司检修公司,合肥 230061)
0 引 言
电励磁同步电机(以下简称EESM)因其功率因数可调、过载能力较强、效率高等优点而成为研究热点,其在水电、火电、船舶驱动、矿井提升等大功率驱动设备上具有广泛的应用[1,2]。EESM控制方法主要有标量控制、矢量控制和直接转矩控制,其中矢量控制根据不同的磁链矢量作为磁场定向矢量又可以分为不同的控制方法。由于EESM正常运行时,一般希望其气隙磁链保持不变[3,4],因此本文采用气隙磁链定向控制方法。
为避免对公共电网的污染和实现能量的双向传输,大功率拖动控制系统会采用能量回馈型交-直-交控制方案,其拓扑结构如图1所示。其中,前级为PWM整流器,其主要作用是提供稳定的直流侧电压、正弦网侧电流和可调的功率因数[5,6]。直流侧电容电压的准确检测是实现前级和整个系统稳定运行的基础。一般直流侧电压都采用传感器配合相应的采样电路进行检测,但当该传感器发生故障或者因采样电路受到干扰而发生采集数据错误时,会影响系统的安全稳定运行,甚至造成设备损坏和人员伤亡等重大事故。因此,获取准确的EESM拖动系统中有源前端整流器的直流侧电压至关重要。

图1 交-直-交拖动系统拓扑图
本文在分析EESM数学模型的基础上,结合EESM的气隙磁场定向矢量控制,研究了一种前级整流器直流侧电压的估算方法。利用估算值进行系统的运行分析,提高了整个EESM控制系统的可靠性。最后通过MATLAB/Simulink进行仿真研究,仿真结果验证了该方法的可行性和正确性。
1 EESM数学模型分析
为建立EESM在两相旋转轴坐标系下的简化数学模型,作以下假设:忽略磁路饱和涡流的影响,绕组的自感和互感保持不变;忽略磁场中的空间谐波分量,沿气隙内的磁动势为正弦分布;忽略电机的铁心损耗,且绕组电阻不随温度和频率的变化而变化。
根据基尔霍夫电压定理和电磁感应定律,可得EESM的磁链方程和电压方程如下:
式中:ωr为转子电气角速度;usd,usq,isd,isq分别为定子绕组的d,q轴的电压、电流;Rs,Re分别为定子、转子绕组电阻;uf,ie为转子绕组电压、电流;urd,urq,ird,irq分别为电机阻尼绕组的d,q轴电压、电流;Rrd,Rrq为转子阻尼绕组d,q轴等效电阻;Lsd,Lsq,Lmd,Lmq分别为d,q轴定子绕组自感、定子绕组与转子绕组间的互感;Le,Lrd,Lrq分别为励磁绕组自感、以及d,q轴阻尼绕组自感。
式中:ψsd,ψsq为定子d,q轴磁链;ψe为转子绕组磁链;ψrd,ψrq为转子阻尼绕组d,q轴磁链。
电励磁同步电机电磁转矩方程:
Te=1.5p(ψsdisq-ψsqisd)
(3)
式中:Te为电磁转矩,p为电机极对数。
2 EESM矢量控制
EESM的矢量控制可以按照转子磁链或气隙磁场定向选定。当采用转子磁链定向时,负载角和定子电压会随着负载的增加而增大,使得功率因数降低。而采用气隙磁链进行定向,则不会出现该情况[6,7]。因此,本文选用气隙磁场定向方法实现EESM电机的控制。
2.1 气隙磁链定向矢量控制
图2给出了采用气隙磁场定向的EESM的矢量图。定子电流矢量is和转子电流矢量ir分别产生定子磁通势矢量Fs和转子磁通势矢量Fr。产生气隙磁链ψ的磁动势Fc是由磁化电流矢量iμ产生的,磁化电流矢量eμ等于定子电流矢量is与转子电流矢量ir之和。磁链轴φ1与气隙磁链同向[1]。

图2 电励磁同步电动机的矢量图
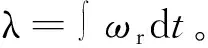
2.2 转矩、磁链和励磁电流控制
根据图2的矢量位置可知,磁链轴与转子轴间的角度为φL,则有:
将式(4)和式(5)代入式(3)中,可以得到电磁转矩表达式:
Te=1.5pψisφ2
(6)
式中:isφ2为定子电流在φ2轴上分量,称为定子电流转矩分量。


图3 交直交EESM控制框图
2.3 混合气隙磁链观测器
采用基于电压电流模型构成的混合气隙磁链观测器观测气隙磁链的幅值与位置信息。该混合气隙磁链观测器结合电流模型磁链观测器(简称IM)优势,并避免了电压模型磁链观测器(简称VM)所存在的问题(诸如积分漂移、初始值等问题)[8-11]。混合气隙磁链观测器的计算框图如图4所示。

图4 混合磁链观测器框图
为获得气隙磁链观测器的电流模型,在忽略阻尼绕组漏抗影响条件下,可以依据式(1)和式(2)得到式(8)、式(9):
将式(8)代入式(9)整理可得:
从式(10)及式(11)可得图4的IM控制框图。图4中气隙磁链幅值|ψ|以及θL可由ψ在d,q轴坐标系上的分量ψsd,ψsq计算得到。
在α,β静止坐标系下,气隙磁链的VM数学模型如下:
改革后的考核方式可以由平时考核模块(作业、英语小测试、实训考核)和综合测试模块(期末闭卷笔试)两大部分组成。平时考核中加入英语测验,主要是考虑到国际结算的专业用语多,在单据、票据和信用证等内容需要用到大量的专业英语,在跨境电商的商品推广,磋商等环节都需要使用专业英语。因此为了提高学生对专业英语的重视程度以及促进其对专业英语的掌握程度,应该增加英语测试。平时成绩满分100分,最终按照40%到50%的比例折算加入期末总成绩。
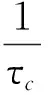
3 有源前端整流器的控制
3.1 有源前端整流器的数学模型
将图1的拓扑中虚线框内的负载等效为RL,具体如图5所示。为了方便分析三相PWM整流器的模型,作以下假设:平衡的三相电网电压,即ea+eb+ec=0;网侧电感为理想的电感,即呈线性且非饱和;功率器件为理想开关管,无开关损耗和压降;三相PWM整流器的交流侧参数对称。

图5 有源前端整流器拓扑结构
定义图5中开关函数Sk(k=a,b,c):
根据基尔霍夫定律,可得有源前端整流器在三相静止坐标系的数学模型:
式中:L,R为交流侧电感值和电阻值;ia,ib,ic为交流侧三相电流;Udc为直流侧电流;RL为直流侧等效负载。
通过Park坐标变换,可得有源前端整流器在两相旋转坐标系下的数学模型:
式中:ed,eq,id,iq分别为电网电压和三相电流在d,q坐标系的分量;Sd,Sq分别为开关函数在d,q坐标系的分量。
3.2 有源前端整流器的解耦控制
由整流器有源前端数学模型式(16)可知,d,q轴变量耦合问题给控制器设计带来一定的困难。为了解决该问题,可以采用前馈解耦控制策略[12]。当电流调节器采用PI调节器时,则控制方程:

4 直流侧电压估算
对于图1中的有源前级整流器,在每一个开关周期内,直流侧电流和交流侧电流满足下式[5]:
idc=Saia+Sbib+Scic
(18)
由式(18)和式(15)可得:
式中:C为图1中的母线电容。
假设当前时刻为第k个采样周期,则式(19)可改写:
Udc(k)和Udc(k-1)分别为当前采样周期与上一采样周期的直流侧电压值,tk和tk-1分别当前采样时刻和上一采样时刻,即tk-tk-1等于一个控制周期tcontrol。
由式(20)可知,若要计算当前时刻的直流电压Udc(k),需要知道负载电阻的大小,而在实际应用中,EESM的输出功率随着负载的改变而改变,因此等效电阻是一个变化值。为了正确估算直流电压,必须正确计算等效电阻RL。按照式(21)可以计算出有源前端整流器当前时刻的输入功率。
在忽略变换器的开关损耗和直流侧电容损耗的情况下,有源前端整流器的输出功率与输入功率相等,即:
将式(22)等号两边进行积分,经过数字化离散处理可以得到:
式中:Pin(k)和Pin(k-1)分别为有源前端整流器当前采样周期和上一采样周期的输入功率。
将式(23)代入式(21)中可以得到式(24):
[Udc(k)-Udc(k-1)]2-H[Udc(k)-
Udc(k-1)]+K=0
(24)
其中:
根据参数H和K及式(24),可以求出直流侧电压当前控制周期的直流侧电压Udc(k):
(25)
可以看出,直流侧电压可以由上一控制周期的直流侧电压值Udc(k-1)与直流侧电压波动值之和得到。
根据以上分析可知,通过当前控制周期的电网电压、三相电流及开关函数可以求得有源前端整流器的直流侧电压的波动值,进而根据上一控制周期的直流侧电压可以估算当前时刻的电压值。由于该方法在推导过程中消除了等效负载RL,故可以在任意负载情况下实现有源前端整流器的直流侧电压的估算。该方法的电压估算值在每个控制周期都会更新,响应速度较快,根据估算值与电压采样值的比较结果进行电压采样值的正确性进行判断,即可实现其容错控制。
5 仿真结果与分析
在MATLAB/Simulink仿真环境中,搭建图3的EESM控制系统,并对其有效性进行验证,具体参数设置如表1所示,其中0.12 s前为整流器起动过程。

表1 控制系统仿真参数
图6为EESM空载正转起动,正转加载,带载减速过程的仿真波形。从图6(a)可以看出,电机的转速在整个过程中都跟随其给定值,在加速或减速过程中,定子电流最大达到限幅值±40A,实现了快速跟随给转速给定的目标。

(a) EESM转速、定子电流φ2轴分量
(b) 网侧电压、电流
图6(b)为有源前端整流器在电机正转加载稳定后的网侧电压和网侧电流的仿真波形。可以看出,有源前端整流器能够实现单位功率因数,且网侧电流具有较好的谐波特性。
图7为EESM空载正转,空载反转,反转加载,反转发电过程的仿真波形。
从图7(a)和图7(b)可以看出,在电机给定从正转(n*=1 000r/min)到反转(n*=-1 000r/min)过程中,定子电流以恒定的数值-40A速度迅速下降并达到给定,体现了系统调节的快速性,而且在这个过程中网侧电压与网侧电流完全反向,实现了能量的回馈。图7(c)为电机反转加载至反转发电过程中的网侧电压和网侧电流关系。可以看出,该系统实现了能量的双向流动以及EESM的四象限运行。图7(d)和图7(e)分别为有源前端整流器直流侧电压在电机反转加载至反转发电过程中的实际值与估算值。可以看出,估算值在稳态及动态过程中的与实际值之间的误差较小。

(a) EESM转速、定子电流φ2轴分量

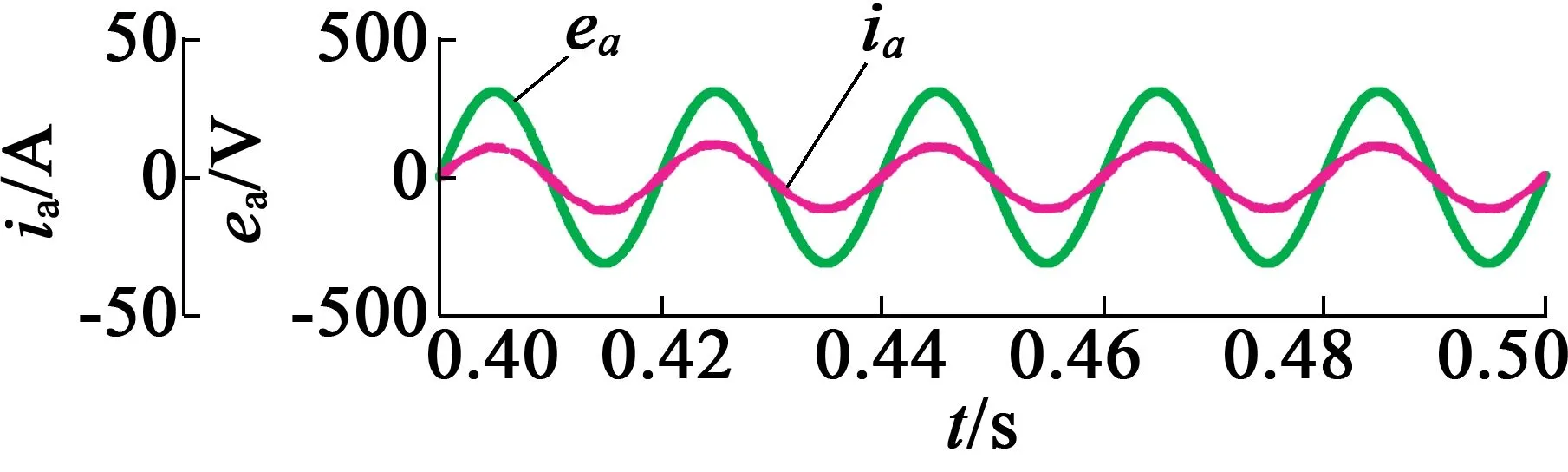
(b) 0.3~0.5 s空载时a相电压及电流仿真波形
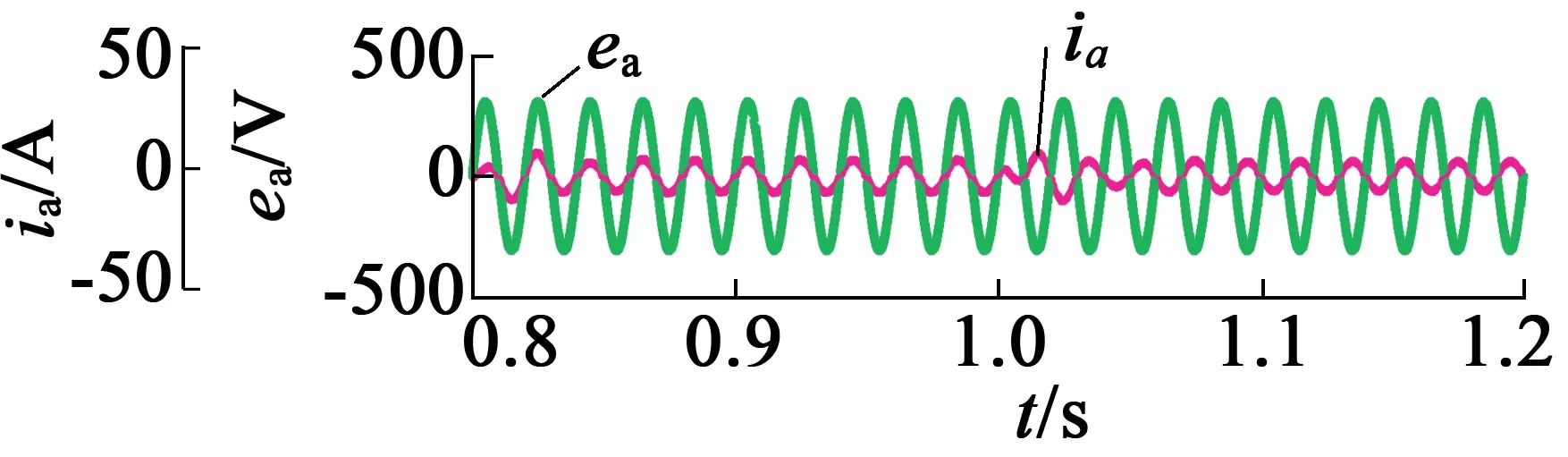
(c) 加载过程中0.8~1.2 s空载时a相电压及电流仿真波形

(d) 直流侧电压实际值

(e) 直流侧电压估算值
为验证所提出的直流电压容错控制方法的有效性,在电机正常工作时,即t=0.95s,在反馈的直流电压值Udc添加100V的偏置量来模拟直流电压反馈通道故障,故障的标志位为Flag。图8(a)和图8(b)为分别为直流侧电压反馈实际值与直流侧电压故障标志位的仿真波形。可以看出,系统可以较快检测出电压反馈数值错误。图8(c)~图8(e)分别为直流侧电压估算值、电机转速及其气隙磁链,可以看出,即使在电压传感器故障时,通过将直流侧电压估算值切入到系统反馈中,使得电机的转速及气隙磁链基本不受影响,实现了系统直流侧电压采样故障检测及其容错控制的目的。

(a) 直流侧电压反馈实际值

(b) 直流侧电压故障标志值

(c) 直流侧电压估算值

(d) 故障前后EESM转速

(e) 气隙磁链圆形轨迹仿真

