考虑乘客选择行为的城轨Y型线交路计划编制

李得伟，刘宗杰，王晓全，兰 贞，刘 宇

(北京交通大学 交通运输学院，北京 100044)

我国城市轨道交通进入网络化发展阶段，随着路网日趋复杂，逐渐出现了一种特殊的线路形式——Y型线，如上海地铁10号线、广州地铁3号线、杭州地铁1号线、大连地铁3号线等。Y型线的运输组织较单线更为复杂，编制科学、合理的列车交路计划是Y型线实现良好运营的基础。合理的列车交路计划不仅能使线路的运力与客流需求得到最佳匹配，还能平衡企业运营成本与旅客出行时间成本，使社会总成本降低。

国内外学者在Y型线列车交路计划编制方面做了许多扎实的基础研究：文献[1]分析了大小交路嵌套对线路通过能力和车底运用的影响；文献[2]以运用车底最少为目标建立了单线上的交路单目标优化模型；文献[3][4]以列车走行公里最小和乘客总候车时间最小为目标建立了多目标优化模型；文献[5]构建了以最小化乘客等待时间、车辆走行公里和列车运行时间为目标的大小交路多目标优化模型。文献[6]提出了交路备选集的概念；吕晓东[7]优化了线网各线列车交路上的发车频率；Ceder[8]通过删减法求解了最优交路。文献[9-16]从实际运输组织角度分析和研究了Y型线路交路的形式和适用条件。

既有研究普遍假设乘客会优先选择直达列车，该假设较理想，未能在实际运营中得到有效支持，所得到的交路计划的实施效果可能不及预期。基于此，本文考虑乘客对直达列车选择有一定偏好的行为，对城市轨道交通Y型线路列车交路计划编制优化模型进行改进研究。

1 问题描述

1.1 Y型线列车交路计划描述

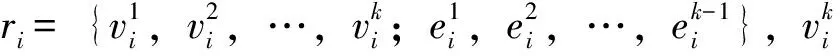
Y型线根据客流量大小或开通时间先后，可分为主线和支线。若根据“两折返站之间线路即可作为交路开行区段”的条件，Y型线路上会形成许多种交路形式组合。但考虑到运输组织复杂性、折返站换乘压力和折返能力等因素，使Y型线路在实际运营中的交路形式不宜过多，且列车不宜频繁折返。因此，Y型线典型的交路形式有3种：独立分段运营、分别直通运营和组合运营，如表1所示。

表1 Y型线典型交路形式

1.2 乘客路径描述

1.3 Y型线乘客对直达列车选择偏好设定

Y型线列车交路计划使线路上的每个OD对之间可能存在不止一条走行路径，乘客在一次OD出行中，既可以选择直达路径也可以选择在中间站换乘。例如：如图1所示为1条Y型线，共有3种交路形式，分别为交路1、交路2和交路3。以起点站为4、终点站为15的乘客，既可以选择直达路径即乘坐交路1，站1—站15上的列车，也可以选择先乘坐交路2，站4—站11上的列车到达站7，然后再换乘交路3，乘坐站7—站15上的列车到达目的地。在现实情况下，这两种选择方式均是合理的。

图1 Y型线交路上直达和非直达路径的选择

为获取乘客对Y型线路上的选择行为特征，本文通过调查问卷对某Y型线路的乘客选择行为特征进行了调研，共回收有效问卷224份。调研发现，存在两种类型的乘客：一类是有直达偏好的乘客(约占60.27%)，当存在直达路径时，这部分乘客会优先选择直达列车乘车，尽量避免换乘；另一类是无偏好乘客，占39.73%，这部分乘客因考虑到不同路径旅行时间相近、拥挤程度的不同(31.25%)，或因未注意到列车开行区间(8.48%)，乘车选择无偏好行为，会选择车到即上。如图2所示。

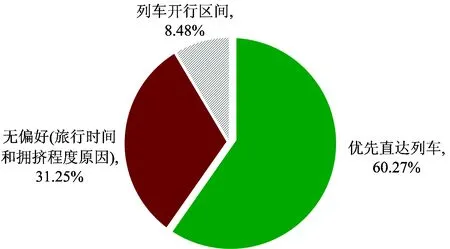
图2 乘客不同偏好选择行为比例

可见，认为所有乘客优先选择直达列车的假设与实际存在一定差距。在进行调查时，虽然乘客是在列车交路计划已知的前提下进行，当交路计划发生改变，乘客的选择很可能发生变化，但简单地认为所有乘客一定会选择直达列车的行为假定显然是不符合实际的。鉴于此，本文中所研究的问题可以定义为：在充分考虑乘客对直达列车选择偏好行为的基础上，构建Y型线交路形式和各交路上发车频率的组合优化模型，最终目标是充分利用有限的运力资源，降低企业成本，更好地匹配运力与不均衡的客流需求。

2 模型与算法

2.1 模型假设与符号定义

1)模型假设

为方便模型构建和求解，建立以下假设：

(1)Y型线具备跨线运营的设备设施条件；

(2)计算时段以h为单位，可分高峰和平峰时段分别计算；

(3)不考虑跨站和越行条件；

(4)各交路列车编组方式均相同；

(5)上下行列车成对开行；

(6)车辆段等配套设施均能满足开行小交路的需求；

(7)乘客只能在折返站进行换乘，列车只能在交路两端的折返站进行折返；

(8)总客流需求不超过输送能力。

2)符号定义

(1)参数

R=(r1,r2,r3，…，rN)：交路集合，ri表示第i条交路，N是交路总数。

Y=(y1,y2,y3,，…，yK)：路径集合，yk第k条路径，K是路径总数。

T：列车交路计划编制的时段长度，h。

α：单位列车购置成本，元/列·min。

β：单位列车走行成本，元/列·km。

lri：交路ri的长度，km。

vri：交路ri上的平均列车运行速度，km·h-1。

zi,o，zi,d：列车在交路两端折返站o和d上的折返时间，min。

g：表示乘客类型，g=1代表乘客优先选择直达列车，g=2表示乘客无直达偏好。

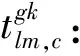
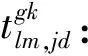
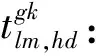
Clm,min为ODlm所有路径中的最小出行时间。

tej：区间ej的行车时间，min。

ajd：乘客进站候车时间系数。

ahd：乘客换乘时间系数。

Ek：路径k上包含的区间ej集合。

Vk：路径k上包含的车站vi集合。

λ：乘客单位时间价值，单位为元·h-1。

qlm：l站为起点，m站为终点的OD对ODlm上的客流量，人次。

P：优先选择直达列车偏好的乘客所占比例；1-P：无直达偏好的乘客所占比例。

Q：列车标准载客人数，人。

Nk:路径k中包含的交路总数。

nmin，nmax：区间可覆盖交路个数的上下限。

hmin，hmax：行车间隔的上下限，min。

fmin，fmax：任一交路形式的发车频率上下限。

Nmin，Nmax：交路总数的上下限。

w：小交路覆盖的车站个数最小值。

η：列车区间满载率。

φ：为企业目标函数的权重，1-φ为乘客目标函数的权重。

M：为一个较大的正整数。

(2)决策变量

δi：0-1变量，交路ri是否被当前解选中，若选中则其值为1，否则其值为0。

fi：第i条交路在单位小时内的发车对数。

2.2 目标函数

Y型线列车交路计划编制的目标函数包括运营企业成本和乘客成本两个方面。

1)企业成本

在能够满足客流需求的前提下，运营企业总是希望尽量节约成本。企业成本主要包括列车购置成本Z1和列车走行成本Z2。其中，购置成本可通过计算需要的列车数量确定。考虑到企业运营的列车包括运用、备用和检修车，因此，设定购置列车数量为运用车数的1.2倍。列车走行成本可通过每种交路的长度和发车频率的乘积来进行计算。两种成本均需相应的费率系数进行转换，得到最终成本，共同作为编制交路计划时企业的目标函数，分别为

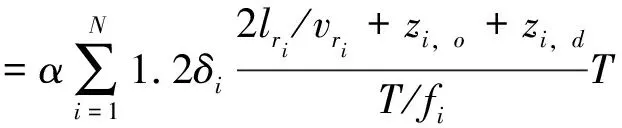
(1)

(2)

2)乘客成本

乘客成本主要指出行时间带来的成本，包括乘车成本、进站候车成本、换乘成本3部分，分别由在车时间、始发站候车时间、换乘时间决定。

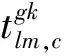
(3)

(2)始发站候车时间为

(4)

(3)换乘时间：指乘客不能在1个交路形式内完成出行时，需换乘到其他交路列车时所花费的时间，包括换乘走行时间和换乘等车时间，换乘走行时间为

(5)

引入乘客对列车选择偏好系数P，按乘客是否具有优先选择直达列车偏好对每条出行路径进行划分，并考虑乘客单位时间价值λ后，乘客出行时间成本为

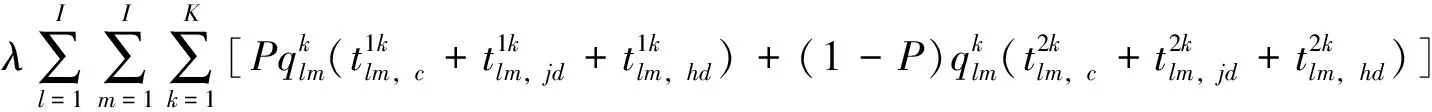
(6)

采用线性加权法将多目标函数转化为单目标函数，以平衡各目标的相对重要性和它们在量级上的差异，即

minZ4=φ(Z1+Z2)+(1-φ)Z3

(7)

2.3 约束条件

模型中的约束条件如下。

(1)线路上所有车站和区间的覆盖交路数量约束

(8)

(2)交路总数约束

(9)

(3)交路覆盖区间数量约束

(10)

(4)任意交路形式的发车频率约束

fmin≤fi≤fmax,ri∈R

(11)

(5)同时被多个交路覆盖区间的行车间隔约束

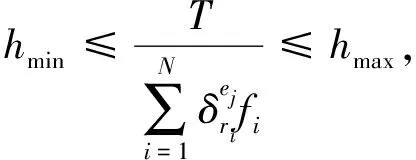
(12)

(6)区间满载率约束

(13)

(7)所有乘客一定被输送约束

(14)

2.4 求解步骤

上述模型为整数规划模型，由于可选交路数量有限，可以设计确定性枚举算法求解，具体步骤如下。

Step1: 初始化。根据折返站设置和约束(1)—(3)选定可能交路的集合，并进行交路组合分支，根据约束(4)—(5)给定每个交路形式上的发车频率组合，得到初始解组合。其中交路个数、发车间隔和发车频率、区间交路覆盖数的上下限均根据实际问题取值。

Step2:路径搜索。采用Dijkstra算法中逐渐向下搜索路径的方法，对起点到终点OD对上的出行路径进行搜索，其中若存在大交路中间站(不包括首末站)被同一小交路覆盖的路径，视为无效路径剔除。

Step3:客流分配。对各OD对上所有的客流进行路径分配，根据分配概率，将ODlm之间的客流分配到不同路径k上，表达式为

(15)

对于具有优先选择直达列车偏好的客流，判断当前OD对上的有效路径中是否含直达路径。若有唯一直达路径，则将所有客流分配到直达路径上，当存在多条直达路径时，根据路径上交路的发车频率比例进行分配，表达式为

(16)

若不含直达路径，采用改进的Logit模型确定每条出行路径客流分配比例，表达式为

(17)

对无优先选择直达列车偏好的客流，根据发车频率将客流分配到不同出行路径上，表达式同式16。

Step4:计算初始解组合中各方案目标函数值，根据δi和fi的取值分别得到每种方案下交路开行区间和各交路发车频率，并选择具有最小目标函数值的方案，作为最优交路备选计划。

Step5: 检查最优交路备选计划中交路计划的可实施性，确定最终的交路计划。

3 案例分析

3.1 案例描述与参数取值

某市城市轨道交通线路1和线路2形成Y型线。车站和区间编号见图3，线路配线见图4。列车区间运行时间和停站时间分别见表2和表3，客流OD见表4，其他参数取值见表5。

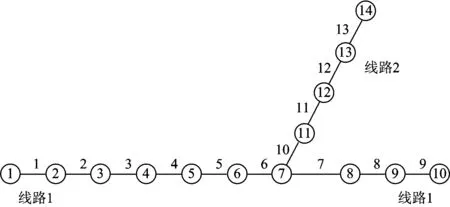
图3 Y型线路

图4 Y型线路配线

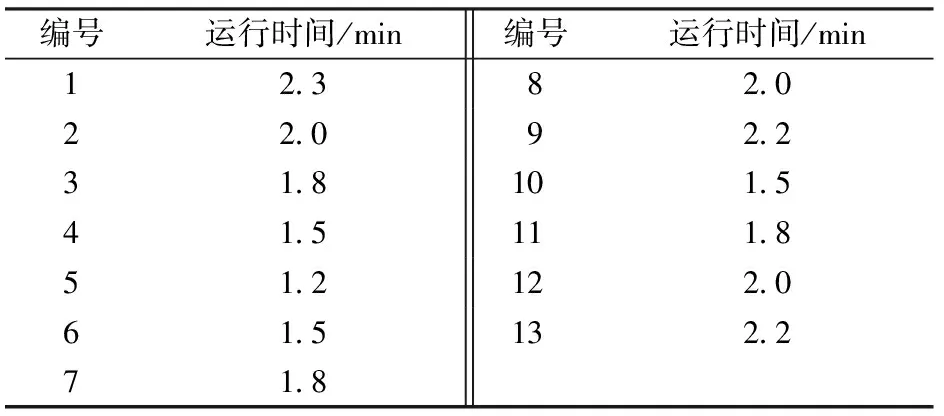
编号运行时间/min编号运行时间/min12.382.022.092.231.8101.541.5111.851.2122.061.5132.271.8

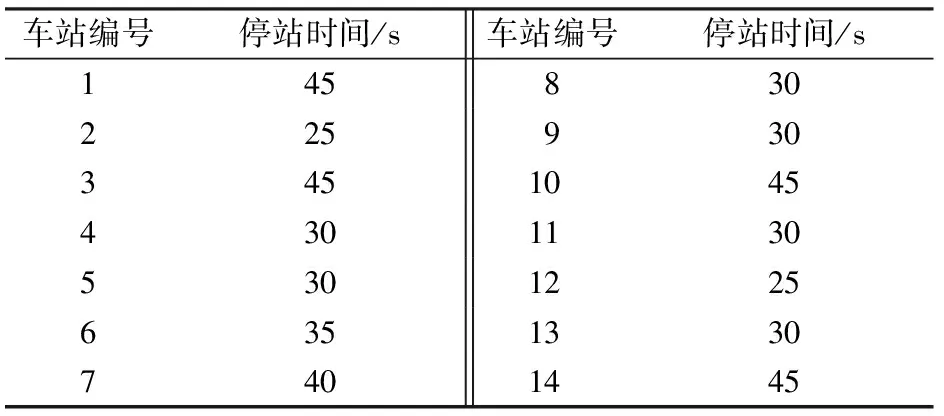
表3 停站时间

表4 OD客流

表5 参数取值

根据图3折返站设置及约束条件(1)，得到满足条件的交路形式共有5个，见表6。

表6 可能的交路形式

3.2 结果分析

利用第2.4节中的步骤求解得到2个交路和3个交路形式下的最优列车交路计划，如图5所示。

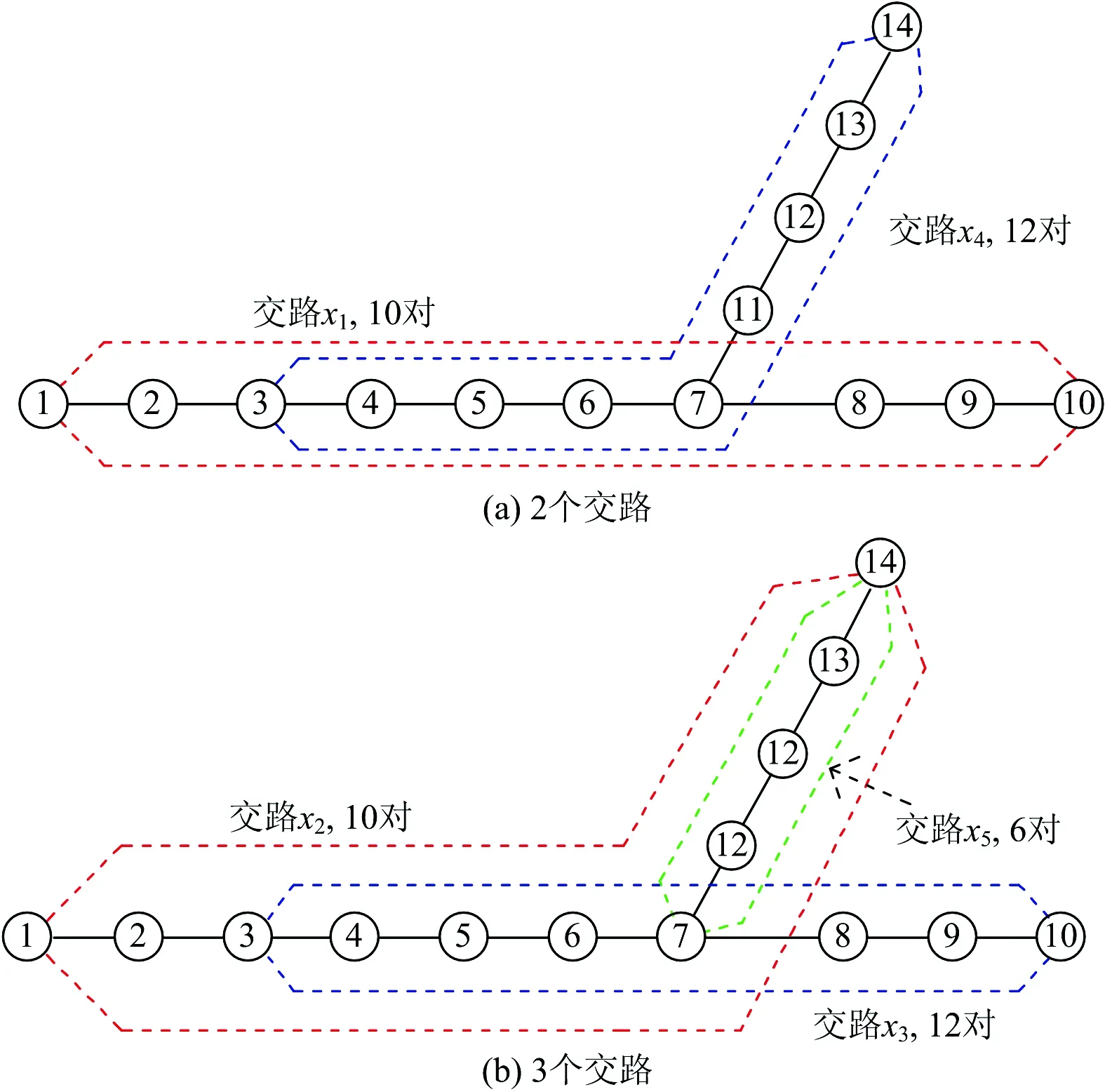
图5 最优列车交路计划

将结果与独立分段交路形式下的最优解(见图6)进行对比，目标函数及分项值见表7。

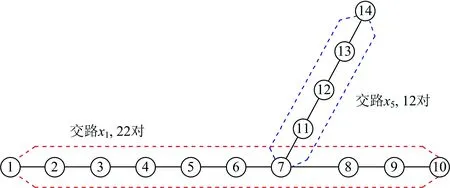
图6 独立分段交路最优列车交路计划

可以看到，与独立分段交路相比，求解得到的2个交路和3个交路最优交路计划的总成本均有所减少。

为了得到最终方案，还需结合客流分布情况做进一步分析。地铁设计规范(GB50157—2013)规定支线在干线上的接轨点不宜设在靠近客流大断面的车站，避免支线客流对干线客流产生突破性冲击。因此，对于具有支线独立交路的方案图5(b)和图6还需要分析支线独立交路对干线各区间客流断面的影响程度。图7展示了有支线独立交路的各断面和车站7的客流变化情况，可以看出，将接轨点设在7号站时，客流大断面所受影响较大，因此，独立分段交路与3个交路的最优交路计划均不符合设计规范规定，最终选择的最优求解结果为2个交路最优列车交路计划，即图5(a)所示的方案。

表7 多交路与独立分段交路比较

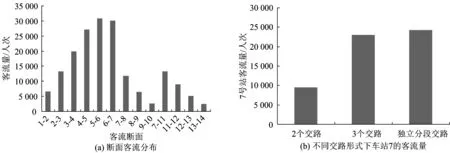
图7 包含支线独立交路的客流断面

4 灵敏度分析

4.1 乘客有无优先选择直达列车偏好参数

为探究乘客对列车选择偏好对交路计划的影响，将乘客对直达列车偏好参数P分别取值0到1，求解对应的最优解。以3个交路形式为例，不同参数取值下的乘客成本变化如图8所示。特别地，将2种极端情况——乘客均无直达偏好和乘客均具有直达列车偏好的求解结果对比如图9所示，目标函数对比如表8所示。

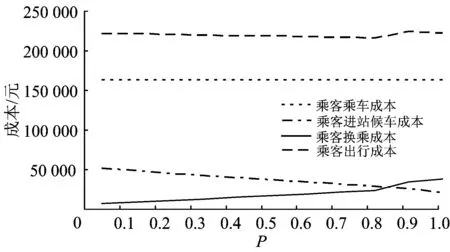
图8 乘客选择偏好对乘客成本的影响

表8 极端偏好最优交路计划比较

图9 极端偏好比例最优解

可以看出，随着P值的增加，乘客换乘成本增加，而进站候车成本和总出行成本减少。与乘客均有直达列车选择偏好相比，当乘客均无直达列车偏好时，最优交路计划明显改变，总发车频率明显降低，企业各项成本也有所减少。

观察图9发现，当所有乘客均具有优先选择直达列车偏好，得到的最优列车交路计划线路上的列车数较多，但直达性较低，此时的最优列车交路计划是用较多的列车对数减少了乘客均优先选择直达列车时的候车等待时间，反之亦然。

4.2 目标函数权重系数

将权重系数φ分别取值为0～1，观察侧重企业运营成本和乘客出行成本策略对Y型线路列车交路计划的影响，求解结果见图10和图11。

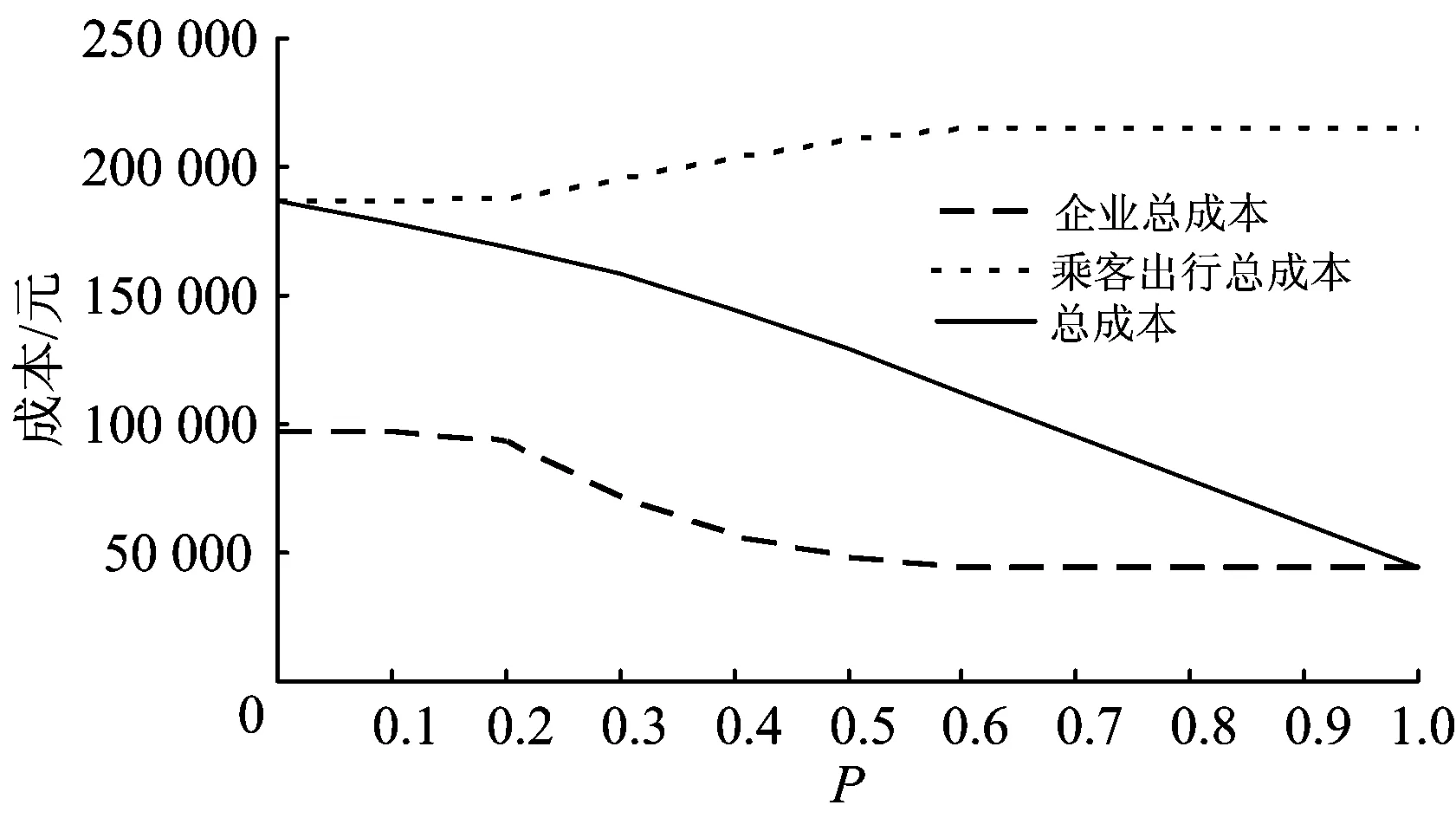
图10 不同权重系数对结果的影响

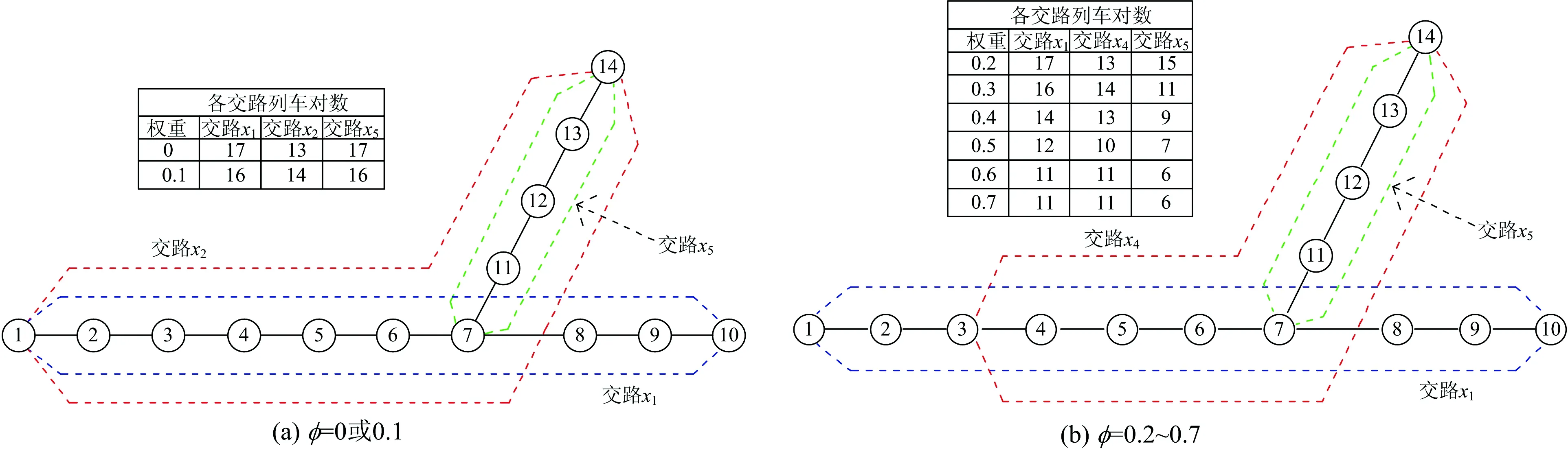
图11 不同φ的3个交路最优解

随着企业运营成本权重φ的增加，发车频率不断降低，使得企业列车购置费用、走行公里换算费用和企业运营总成本均不断降低，乘客进站候车成本、换乘候车成本和出行总成本均不断增加。

随着φ的增加，分段交路x5(站7—站14)会向着跨线交路x4(站3—站14)转变，说明当交路计划编制侧重企业一方时，开行跨线交路能有效减少发车频率，降低企业运营成本。

5 结 论

为研究乘客直达列车选择偏好对Y型线列车交路计划编制的影响，本文建立了Y型线列车交路计划编制模型，设计了求解算法，优化了交路形式和发车频率。通过案例研究和灵敏度分析发现，随着乘客直达列车偏好的下降，区间覆盖交路数增加，发车频率、企业成本降低，乘客总出行时间增加，在实际Y型线列车交路计划编制中应充分考虑这一影响。未来的研究方向主要包括几个方面：①考虑帕累托最优的合理权重取值确定方法；②展开更大规模的调研，在更大范围内验证乘客选择行为偏好理论；③适合大规模的更高效率求解算法；④多种乘客类型和停站组合条件下的交路计划编制。