毛细透排水管排水渗流模型及设置间距研究
郭一鹏, 冷伍明,杨 奇,赵春彦,昌 思
(1.中南大学 土木工程学院,湖南 长沙 410075;2.中南大学 高速铁路建造技术国家工程实验室, 湖南 长沙 410075;3.中国铁路设计集团有限公司, 天津 300251)
路基边坡的病害有多种,形成病害的因素亦很多,但水的作用是最主要的因素[1]。有 “十滑九水”、“治坡先治水”之说。2013年铁路总公司秋检报告指出[2],全国铁路灾害总计有68 999处,长14 107 km,其中水害占比为38.5%。主要原因是排水不良,传统排水结构失效[3]。无疑,提高路基边坡排水能力,或开发可替换的排水结构如PVC管,显然具有重要意义和广泛应用前景。毛细透排水管是一种新型排水管,它是由特制的PVC或PE管外裹1层毛细透排水带构成(毛细透排水带是近年我国台湾技术人员开发的一种新型排水材料[3],其排水通道横截面形如字母“Ω”,不仅能主动排水,还能有效防止土颗粒流失),如图1所示。这种新型排水管具体设置方法为:按一定仰斜角钻孔置入排水管管段,通过其特殊的结构为边坡中水分提供排水通道,从而实现全长排水。试验和工程应用证明,它比传统的PVC排水管功能强、效率高,排水时不易带走土颗粒和堵塞排水通道,且可分段置入,在既有线旁施工不中断行车。此种方法引起了铁路运营管理部门和技术人员的高度关注,并已在铁路工务部门得到示范和推广使用。

图1 毛细透排水管
目前国内对构成这种新型排水管的毛细透排水带的排水能力和抗淤堵开展了一些研究。凌贤宗等[4]研究了不同渗透系数下毛细透排水带的排水和反滤能力。陈宵等[5]通过排水带在淤泥中的排水效果研究了其抗淤堵的能力。张素磊等[6]通过公路隧道渗漏水治理项目检验了毛细透排水带的有效性。但对处治铁路路基边坡水害的设计、计算方法的研究尚处于起步阶段,其排水间距、直径等参数的选取大多依靠工程师的判断和经验,并没有一套完善的设计方法,因此开展这方面的研究具有重要意义和工程应用价值。本文通过建立毛细透排水管排水渗流模型,推导其不同排水条件下排水间距的计算方法。
1 地下水运动基本方程
文献[7-9]表明,考虑蒸发作用,排水管的排水间距可放大14.7%~39.7%。南方地下水富集,降雨量大,植被茂盛,蒸发作用对地下水位的影响相对薄弱;且考虑蒸发作用,计算相对复杂,不便工程运用。为此,研究中将蒸发的影响作为储备,仅考虑地下水运动。


图2 排水管排水模型


图3 地下水运动方程推导简图
假设水是不可压缩的,根据连续性原理,这2个水量的变化量应相等,即:
(1)
(2)
式(2)为地下水运动基本方程。对于均质各向同性,则整理式(2)得
(3)
2 排水渗流模型
2.1 稳定渗流模型
若同一时间内入渗补给水量与排水量相等,且不随时间变化,则地下水运动为稳定流,渗流模型如图4所示。图中:H0为排水管高度;hc为水位最高点高度。

图4 稳定渗流模型
(4)
求解式(4)可得排水管间的浸润线方程为
(5)
2.2 非稳定渗流模型
当入渗补给水量大于排水管排水能力时,地下水位不断上升,当降雨停止后,地下水位降低。在排水管作用下,地下水位、排水量以及浸润线均随时间变化,此时地下水运动不再是稳定状态,有必要建立不同条件下的非稳定渗流模型,用于计算排水管排水间距、时间等参数。
2.2.1 地下水位下降
降雨停止,W=0,表示排水管间地下水运动的方程式(3)化简为
(6)

(7)
降雨停止时,地下水位相对于两排水管所在平面距离为h0。设h=H-H0为排水管间任意一点、任意时刻相对于两排水管所在平面水位(m),则地下水位下降的非稳定渗流模型如图5所示。
地下水位下降的非稳定渗流基本方程为
(8)

(9)

图5 地下水位下降渗流模型
式(9)可通过Laplace变换和Fourier变换2种途径进行求解。张蔚榛[14]对Laplace变换以误差函数形式求解的方法做了较为全面、系统的研究,因此本文将采用傅里叶级数形式进行求解。
对式(9)关于t进行Fourier变换,求得排水管间的浸润线方程为
(10)


2.2.2 地下水位上升
当地下水水位与两排水管所在平面平齐时,排水管停止排水。若有降雨补给,地下水位将上升,排水量将发生变化,此时渗流模型如图6所示。

图6 地下水位上升渗流模型
地下水位上升的非稳定渗流基本方程为
(11)
(12)
式(12)同样可通过Fourier变换求解,得排水管间的浸润线方程为
(13)
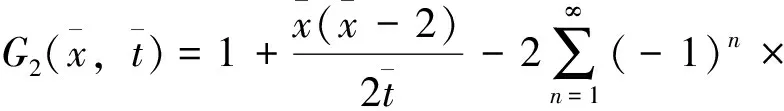

3 设置间距
本节根据上面得到的渗流模型讨论不同渗流状态下毛细透排水管的一些特点及设置间距。
3.1 稳定渗流状态
分析浸润线方程式(5)可知,当W>0时,为椭圆曲线,当W<0时,为双曲线,当W=0时,为抛物线。有入渗补给水量时,毛细透排水管间的浸润线方程为一椭圆曲线的上半支,毛细透排水管间形成分水岭,即x=L/2处水位最高。代入式(5)求出水位的最高点hc为
(14)
地下水位过高,易形成路基塌陷,边坡滑坡等病害。基于此,可设产生病害的临界水位为Hcr,此时hc=Hcr-H0,代入式(14)可求排水管间的临界间距Lcr为
(15)
即当排水管设置间距L 根据Darcy定律,流入单位长度排水管内的水量为 (16) 根据式(16)可确定排水管的排水直径。 3.2.1 地下水位下降 (17) 根据Darcy定律,流入单位长度排水管内的水量为 (18) 3.2.2 地下水位上升 (19) (20) 对比式(20)与式(5)可知,由非稳定渗流模型(地下水上升)推导的浸润线方程与稳定渗流状态下的相吻合,表明稳定渗流模型是非稳定渗流模型的一种表现形式,即,地下水位上升下毛细透排水管的间距可采用稳定渗流状态下的解析解。 排水管间距为 (21) 此时流入单位长度排水管内的水量由式(16)计算。 利用以上研究成果,进行毛细透排水管处治京广线K2058+135—+740边坡水害的设计工作。 京广线K2058+135—+740位于广东省韶关市境内,属南岭山脉,高温多雨,年平均降雨量为1 700 mm,表层土质厚2~5 m,渗透性较差。坡脚为重力式挡土墙,墙高2~8 m。在干旱季节,墙身多水渍,局部渗水严重,相应位置泄水孔无水流。该段边坡汇水面积大,加之当地常发生强降水,致使边坡局部时常发生滑坍破坏,危及行车安全。设计方案采用毛细透排水管排除边坡中的地下水,并设置水位管观测地下水位。已知条件[15]:边坡内初始水位H=4.6 m,毛细透排水管位置H0=0 m,设计要求边坡水位降低2.1 m,边坡土体渗透系数k=0.003 8 m·d-1,入渗补给量W=0.09 m·d-1(可由降雨前后水位管变化近似推算)。 降雨过程,地下水位上升,采用地下水位上升的非稳定渗流模型或地下水稳定渗流模型,将上述参数代入式(15),得排水间距为1.89 m。本研究建立的渗流模型将蒸发作为储备考虑,计算值存在一定富余,同时为便于施工定位,本工程将毛细透排水管设置间距取为2.0 m。毛细透排水管安装后,对其排水量进行监测,其计算值与实测值对比如图7所示。 图7 排水量的计算值与实测值 由图7可知,实测结果与理论计算值吻合较好,表明该方法合理有效。 基于地下水运动基本方程,建立毛细透排水管的稳定渗流模型(地下水位恒定),非稳定渗流模型(地下水位下降或上升)。针对2阶非线性的非稳定渗流模型,采用使方程线性化,Fourier变换的方法推导了不同渗流状态下的浸润线方程。通过浸润线方程,得到了不同渗流状态下的排水间距及排水量的解析解。最后经实例验证了解析解的准确性。该模型能够反映地下水运动的基本规律,计算简单,针对性强。研究成果深化了其排水机理,并可为毛细透排水管的设计提供一定的指导和借鉴。3.2 非稳定渗流状态


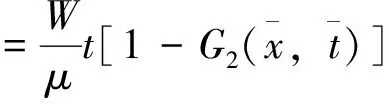

4 工程应用

5 结 语

