基于贝叶斯MCMC方法的洪水频率分析及不确定性评估

吴云标，迟艺侠

(1.河海大学水文水资源学院，江苏南京210098；2.河海大学文天学院，安徽马鞍山243031)

近几十年来，洪水事件被认为是世界上最普遍、分布最广泛的自然灾害之一，洪水灾害是影响经济社会可持续发展的障碍性因素之一[1]。因此，洪水频率分析已成为水文学中的一个研究热点。在洪水频率分析中，洪水设计值的计算和不确定性评估是水利工程规划和水资源管理的一个重要课题[2]。

极值理论(EVT)是研究极端事件最为成功的方法之一，在水文、气象、地震、保险、金融等领域得到广泛的应用[3]。在极值理论中，独立同分布随机变量的区组最大值分布的渐近分布为广义极值分布(GEV)[3-5]。传统的GEV分布参数估计有极大似然估计(MLE)法、矩法、L-矩法等，其中极大似然估计法最为常用[6-7]。Martins等[8]研究表明，小样本的极大似然估计不稳定，形状参数的估计有时会偏小，导致分位数与观测值的均方根误差偏大。Coles[4]也指出极大似然估计法虽然是从考虑不确定性出发，可以用来计算参数的置信区间，但由于极大似然估计量以渐近正态为基础，除非样本足够大，否则不足以说明这种不确定性。近年来，国内外围绕小样本参数估计和不确定性评估的研究取得了较大的进展，其中贝叶斯估计法最具有代表性[9]。与传统的参数估计法中将分布参数作为确定性未知常量不同，贝叶斯估计法将未知参数看成随机变量，在对总体分布参数进行统计推断时，除了样本提供的信息外，还需在抽样前确定总体分布参数的先验分布，即使样本序列较短，也能获得比较精确的推断结果[9-10]。近年来，贝叶斯估计法已逐步被引入到洪水频率分析中。Kuczera[11]根据贝叶斯理论，运用重要性抽样法搜索参数的后验状态空间计算洪水的置信区间。O'Connell等[12]利用贝叶斯理论将历史和古水文信息等考虑到洪水频率分析中，发现古水文信息能有效减少分位数估计偏差且能缩小设计洪水估计的不确定性。Liang等[2]基于贝叶斯理论，将模型不确定性和参数不确定性同时纳入洪水频率分析，对分位数的不确定性进行了有效估计。

本文以GEV分布为洪水频率分布线型，利用基于贝叶斯理论的MCMC模拟方法，研究洪水高分位数设计值的推求方法，得到相应的置信区间，从而对估计值的不确定性进行定量评价，并以洞庭湖流域四个水文站点洪水频率分析为实例，验证方法的有效性。

1 研究方法

1.1 贝叶斯参数估计

1)贝叶斯公式

假设样本x=(X1,…,Xn)的密度函数属于参数族F={f(x;θ):θ∈Θ}，其中参数θ是一个未知的常数。在经典的统计推断中，在得到样本x之前，对参数θ是一无所知的。在贝叶斯框架下，总体参数θ被当作随机变量，根据历史资料或经验，给出参数的概率密度函数π(θ)，称为θ的先验密度。贝叶斯公式将先验信息与样本信息进行耦合，如式(1)。

其中：π(θ)和f(θ|x)分别为参数θ的先验和后验密度函数；f(x|θ)为样本x=(X1,…,Xn)的似然函数；是θ的参数空间。

2)先验分布

先验分布π(θ)的确定是贝叶斯分析的关键，目前主要采用一些经验的方法。如：在无历史数据以及经验的情况下，按照贝叶斯理论的无信息先验分布的原则，可认为θ服从均匀分布；若参数θ倾向于取较小的实数值，则可用具有较大方差的正态分布表示[4]。

3)似然函数

Xi=(i=1,…,n)相互独立，样本x=(X1,…,Xn)的似然函数f(x|θ)可用式(2)计算。

4)后验分布

后验分布f(θ|x)由先验分布π(θ)和似然函数f(x|θ)通过式(1)确定。

5)参数估计

在贝叶斯理论中，总体分布参数θ的统计完全由后验分布推断，不需要借助极大似然估计的渐近正态性来得到参数估计量的渐近分布。取后验分布的均值作为θ的估计值。

1.2 洪水设计值计算

假设洪水观测值x已知，观测值为x时θ的后验分布用f(θ|x)表示，如果用z表示未来洪水设计值，则z的预测密度可表示为

与其他的预测方法相比，其优点在于它包含了反映模型不确定的f(θ|x)，以及反映未来观测值变异性的f(z|θ)。

由式(3)可得洪水的未来分布

其中含有参数的不确定性和未来观测值的随机性。解方程可得m年重现水平的洪水设计值（即分位数）。

方程(5)中后验分布的计算较复杂，即便是用数值积分方法计算也比较困难。近年来模拟方法的快速发展为该问题的解决提供了新途径，Markov Chain Monte Carlo（MCMC）法为其中有效方法之一[3]。本文采用MCMC法模拟产生服从后验分布的随机样本，去除前k个不稳定的样本，将剩余序列θk+1,θk+2,…,θn看作f(θ|x)的观测值。

由式(4)得

再由数值方法求解得式(5)的解。

1.3 MCMC方法

MCMC方法的思想是通过建立Markov链模拟产生服从后验分布的随机样本，从而模拟样本估计的后验分布[3]。该方法通过迭代产生模拟序列θ0,θ1,θ2,…，其中θ0为任意初始值，θi+1由条件分布q(·|θi)产生，即θi+1只依赖于当前的θi，与前面的θ0,θ1,θ2,…,θi-1无关。不同的抽样方法形成不同的Markov链，其中Metropolis--Hasting算法是目前应用最为广泛的MCMC抽样方法之一，其基本步骤如下：

1)确定参数的初始值θ0，选定建议分布q(·|θi)；

2)由q(·|θi)产生一个新的建议值θ*；

3)计算接受概率αi

4)以概率αi接受θ*为下一个θi+1，即

其中μ为[0,1]均匀分布随机数。

重复步骤2)~4)直到产生足够多的样本为止(样本数为n)，去除前k个不稳定的样本，使得剩余的序列θk+1,θk+2,…,θn达到平稳状态，则此序列可认为是后验分布的抽样，并用来估计后验分布的数字特征。

1.4 GEV分布

GEV分布是Gumbel、Fréchet和Weibull分布3种极值分布的统一形式[3-5]，其分布函数为

其中：μ,σ,ξ分别表示GEV分布的位置、尺度、形状参数，满足

2 实例分析

洞庭湖流域位于长江流域中下游，总面积约为26万km2。流域内径流年际变化大，旱涝灾害发生几率高[13]。本文选取流域内四水(湘江、资水、沅江、澧水)主要水文控制站点(湘潭站、桃江站、桃源站、石门站)年最大洪水流量作为研究对象，其中：石门、桃江站流量资料为1951—2014年，桃源站为1953—2014年，湘潭站为1951—2012年。

2.1 洪水频率分布选择

在水文频率分析中，洪水频率通常采用GEV分布、皮尔逊III型(P-III)分布来分析。为从上述分布中选择一种最佳概率分布，分别对洞庭湖流域内四个站点年最大洪水流量用上述待选分布进行拟合。为便于计算，年最大洪水流量单位统一为103m3·s-1。

采用均方根误差(RMSE)检验洪水频率曲线的拟合效果，RMSE值越小表示拟合效果越好。计算如式(10)。

分别采用两种待选分布对四个站点年最大洪水流量进行拟合，其拟合效果检验的RMSE值见表1，其中GEV分布参数估计采用极大似然法(MLE)，P-III分布参数估计采用矩法。由表1可知，除石门站P-III分布拟合的RMSE值略小于GEV外，其余3个站点GEV分布拟合的RMSE值均小于P-III分布，说明GEV分布对4个站点年最大洪水流量拟合有良好的适应性。由于石门站P-III分布和GEV分布拟合结果接近，为便于分析，石门站仍采用GEV分布。

表1 各站点年最大洪水流量概率分布拟合效果RMSE检验值Tab.1 RMSE values of probability distribution fitting effect of annual maximum flood flow distributions at each station

2.2 GEV分布参数的贝叶斯估计

分别对石门、桃源、桃江、湘潭4个水文站的年最大洪水流量建立GEV分布模型。采用Metropolis-Hastings算法产生随机样本，用去除前k个不稳定样本后的序列对GEV分布参数进行统计推断。选择先验密度函数为π(μ,σ,ξ)=πμ(μ)πσ(σ)πξ(ξ)，其中：参数μ,σ,ξ相互独立；πμ(μ),πσ(σ)和πξ(ξ)为均值为，方差分别为vμ,vσ,vξ正态分布的概率密度函数。为使密度函数平坦，选择足够大的方差，按照文献[4]的建议，选取vμ=vσ=104,vξ=102。参数μ,σ,ξ的建议分布为各自坐标轴上的随机游动，即μ*=μ+εμ,σ*=σ+εσ,ξ*=ξ+εξ,其中εμ,εσ,εξ为均值为0，方差分别为ωμ,ωσ,ωξ的正态随机数。在实验中，通过调整ωμ,ωσ,ωξ的值，使接受概率αi落在0.2~0.5之间[14]。为使MCMC快速收敛，本文选择GEV模型参数的极大似然估计值作为参数μ,σ,ξ的Metropolis-Hastings抽样初始值。

以石门站为例。图1为石门站年最大洪水流 量GEV模型参数经过10 000次迭代产生的MCMC序列图。从图中可以看出，由极大似然估计值作为初始值生成的序列收敛很快，均在初始值附近就趋于稳定，说明极大似然估计值作为抽样的初始值合理，且算法效率高。为确保序列的平稳性，去除前500个样本，将剩余序列的模拟值作为后验分布的观测值。

图1 石门站GEV分布参数MCMC模拟Fig.1 MCMC simulation for parameters of GEV model at Shimen station

表2为4个站点基于贝叶斯理论MCMC法的GEV分布参数后验分布的统计特征(置信水平为95%)和参数抽样的初始值(MLE值)。与传统参数的估计方法相比，贝叶斯法不仅给出了参数的估计值，还给出了参数估计值的置信区间，从而能量化模型参数估计的不确定性。

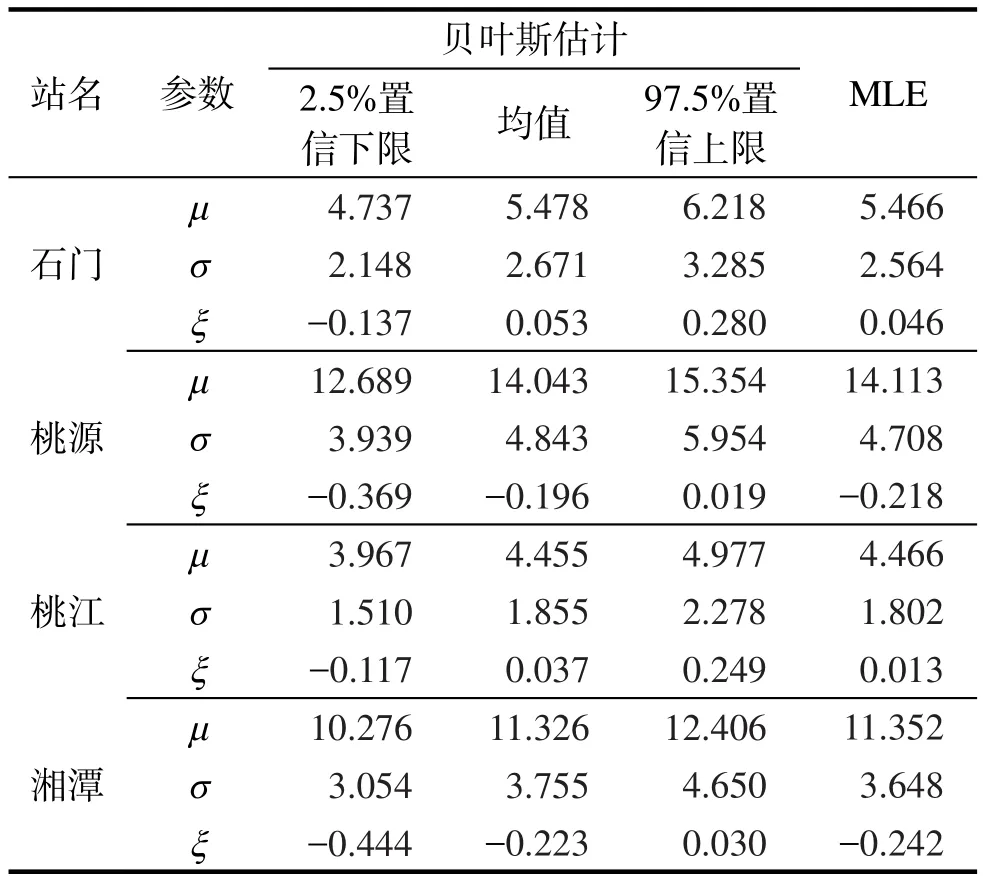
表2 各站点GEV分布参数估计Tab.2 Estimation parameters of GEV distribution at each station

2.3 拟合检验

以石门站为例。图2给出了石门站年最大洪水流量的GEV模型贝叶斯估计分位数拟合效果图。从图中可以看出，样本分位数和理论分位数均分布在45゜线附近，表明GEV模型与实测样本序列拟合效果较好。

对4个站点拟合结果分别采用均方根误差(RMSE)、Kolmogrov--Smirnov检验(K-S检验)[4]进行拟合优度检验。表3给出的是四个站点拟合优度检验结果。从表3中可以看出，贝叶斯估计法和极大似然估计法均通过K-S检验(显著水平α=0.05)。说明两种估计方法均适用于GEV模型参数估计。对比各站点采用两种参数估计方法所得的RMSE可以看出，石门、桃源、桃江站由贝叶斯估计得到的RMSE略大于极大似然估计，但是相差非常小，相差最大的石门站仅为0.065 1，说明贝叶斯估计和极大似然估计结果近似相同。而在湘潭站，贝叶斯估计得到的RMSE略小于极大似然估计，说明贝叶斯估计拟合略好于极大似然估计。总体来说，两者拟合效果基本一致。

图2 石门站GEV模型贝叶斯估计分位数图Fig.2 Quantile plots for the GEV model at Shimen station

表3 各站点拟合优度检验结果Tab.3 Results of goodness-of-fit test of each station

2.4 重现水平估计

当GEV分布模型建立后，T=1/p年重现期的重现水平x1-p可由下式计算

分别将各站点模型参数μ，σ，ξ的模拟值代入式(11)，可得到相应于T=1/p年重现期的重现水平(设计洪水)后验分布样本。

图3给出了石门站各典型重现期下的年最大洪水流量后验密度估计。根据后验密度估计，计算流域内四个站点各重现期下的设计洪水流量及95%的置信区间。其结果如表4。

表4位采用贝叶斯法对4个站点年最大洪水流量不同重现水平的估计。由表4可以看出，贝叶斯法估计的洪水设计值均小于置信区间的平均值，说明置信区间不关于设计值对称。在实际中，由于大洪水资料有限，洪水设计值上限的不确定性通常大于下限的不确定性[10]。这说明贝叶斯法估计的结果与实际相符。此外，从表4还可以看出，重现期越大，对应的设计值越大，相应的置信区间越宽，表明其不确定性越大。

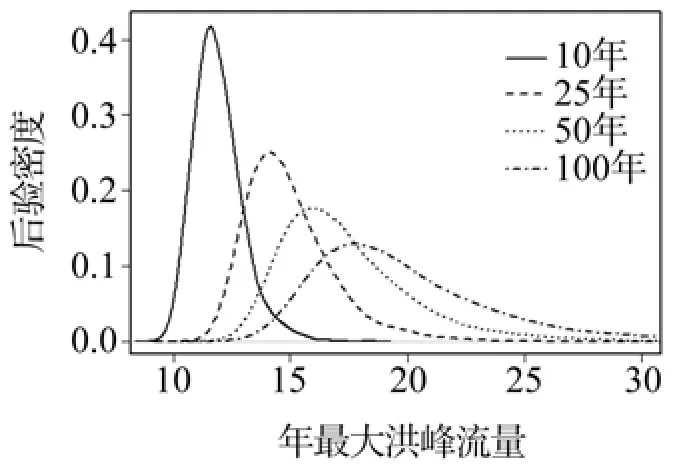
图3 石门站各重现期年最大洪水流量的后验密度估计Fig.3 Posterior density plots of annual maximum flood flow under different return periods at Shimen station

表4 各站点年最大洪水流量的不同重现水平估计Tab.4 Different return level estimates of annual maximum flood flow at each station

3 结 论

以GEV分布作为洪水分布线型，利用基于Metropolis-Hastings抽样的贝叶斯MCMC方法估计GEV分布参数，推求洪水设计值的点估计和区间估计，应用于洞庭湖流域内四个水文站点洪水频率分析，得以下结论。

1)以GEV分布参数的极大似然估计值作为Metropolis-Hastings抽样初始值可有效提高MCMC方法收敛速度。

2)通过贝叶斯MCMC方法，可获得洪水分布参数的后验分布和洪水设计值的后验分布。与传统方法相比，本文方法不仅能得到洪水设计值的估计值，也可得到设计值的置信区间，从而可对估计结果的不确定性进行定量评价。

3)基于贝叶斯法估计的洪水设计值小于置信区间的平均值，置信区间上限与估计值的距离大于置信区间下限与估计值的距离。这种不对称性比传统方法更贴近于实际，说明贝叶斯法估计进一步提高了洪水频率分析结果的可靠性。