类2α分数阶微分方程边值问题的奇摄动

朱红宝

(安徽工业大学数理科学与工程学院，安徽马鞍山243002)

奇异摄动问题多年来一直是学术界关注的热点问题，其摄动方法已成功地应用于自然科学的多个领域[1-2]。近年来，研究者尝试将奇摄动问题与分数阶微分方程理论相结合，如：Beyer等[3]将分数阶微分问题运用到具有阻尼的物理运动中，诠释了物理上有关震动问题；Thandapani等[4]研究一类分数阶偏微分问题的奇摄动，给出了解的形式及分数阶偏微分问题在实际问题中理论意义；Odibat等[5]运用变分迭代方法研究一类分数阶奇摄动问题；莫嘉琪[6]研究一类非线性奇摄动分数阶微分方程的渐近解，得出解的渐近展开式并给出了解一致有效估计；冯依虎等[7]研究分数阶奇摄动微分问题的渐近结论，利用伸展变量法构造出解的形式展开式，证明了解的一致有效性。分数阶微分问题的研究，解决了物理上的诸如具有阻尼的震动问题、复杂的热传导现象等用常规导数的微分方程所不能描述的问题，从而具有广泛的实际意义。

倪明康等[8]利用边界层函数法讨论了如下二阶半线性微分方程(ε>0，为小参数)的第一类边值问题：

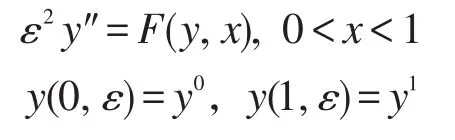
在特定假设下，构造了问题的形式渐近解，并证明了解的一致有效性。本文将该问题推广到分数阶微分问题，利用奇摄动理论构造一类分数阶微分方程的渐近解，并用微分不等式理论证明渐近解的一致有效性。

探讨2α分数阶奇异摄动边值问题：

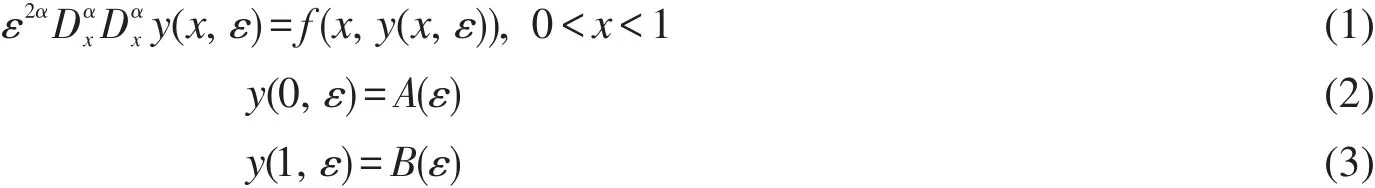
这里ε为很小的正数，函数y(x)的α分数阶导数定义为

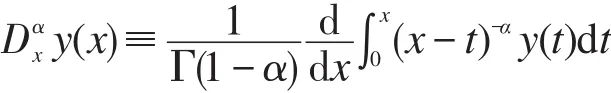
其中：Γ为Gamma函数；α为小于1的正分数。

假设：

H1函数f(x,y)及A(ε)，B(ε)是关于其变量在其定义域内为足够光滑函数；

H2退化问题f(x,y)=0仅有唯一单调解y0=φ(x);

H3函数f(x,y)在范围内满足不等式，其中c为正的常数。

由于退化问题f(x,y)=0是代数型，在以上假设下，其解一般不能满足边值条件(2)~(3)，在x=0和x=1处会产生边界层。

1 形式渐近解的构造

用边界层函数法构造2α分数阶奇摄动边值问题(1)~(3)的渐近解y(x,ε)，令

其中

为正则级数；

为x=0附近边界层级数；

为x=1附近边界层函数。

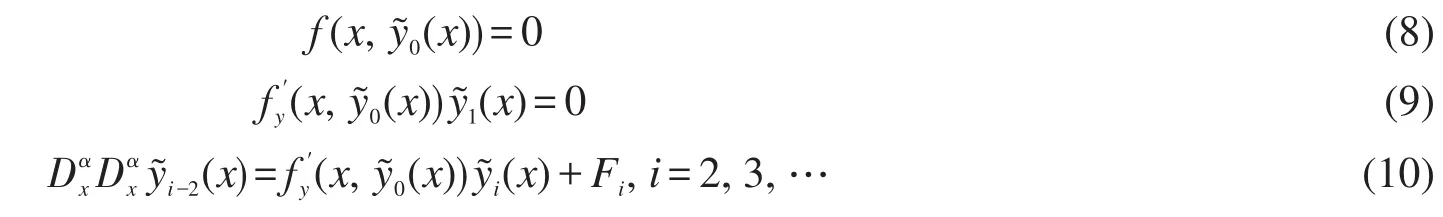
由假设 H2知：,式(10)为代数方程，可依次得，其中的Fi是依次已知的函数。将代入(5)，得原问题的正则项。

在x=0附近的边界层函数由以下方程决定：

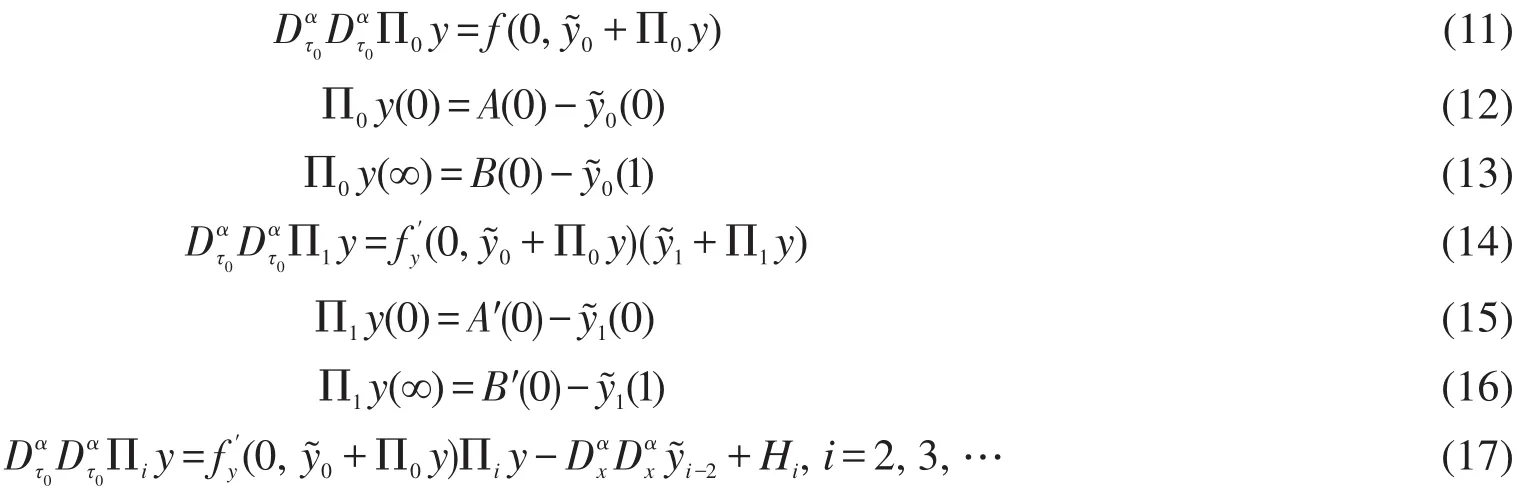
其中

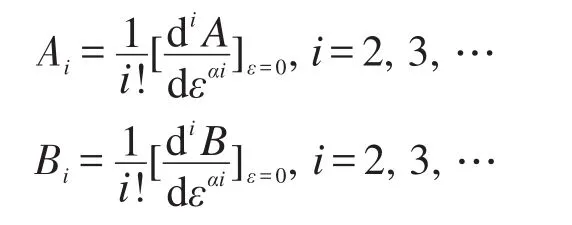
Hi为已知函数。由分数阶微分方程(11)，可得如下Volterra积分系统：

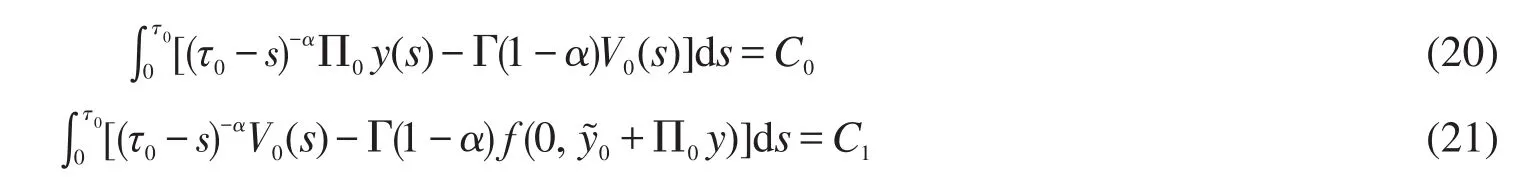
其中C0，C1为任意常数。解此Volterra积分系统并结合条件(12)~(13)得Π0y(τ0)及C0和C1。将求出的Π0y(τ0)代入式(14)，可化为广义的 Volterra积分-微分方程，结合条件(15)~(16)可求出 Π1y(τ0)，类似可得Π2y(τ0)…，且 Π0y(τ0)，Π1y(τ0)，…在x=0 附件具有激波层性态[9]：

其中ki+1≤ki，i=0,1,…为正常数。将 Πiy(τ0)代入式(6)，得原问题在x=0附近的边界层级数 Πy(τ0,ε)。

类似地，在x=1附近的边界层函数由以下方程决定：

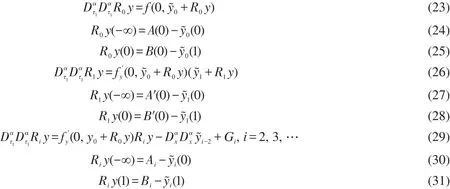
其中

Gi为已知函数。由分数阶微分方程(23)，得如下的Volterra积分系统：

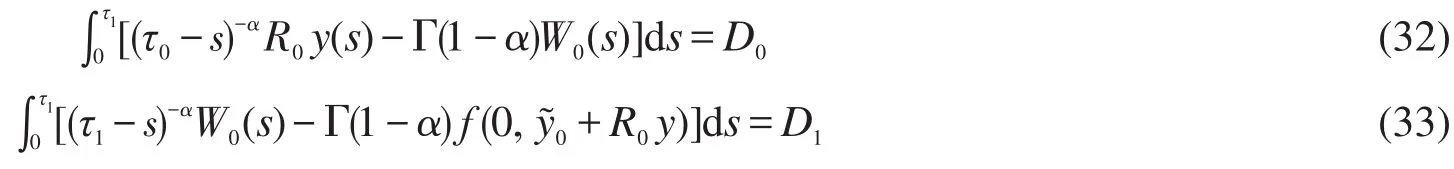
其中D0，D1为任意常数，解此Volterra积分系统(32)～(33)并结合条件(24)~(25)得R0y(τ1)及D0和D1。将R0y(τ1)代入式(26)，可化为广义的Volterra积分-微分方程，结合条件(27)～(28)可求出R1y(τ1)，类似地可依次求出R2y(τ1)…，且R0y(τ1)，R1y(τ1)，… 在x=1附件具有激波层性态[9]：

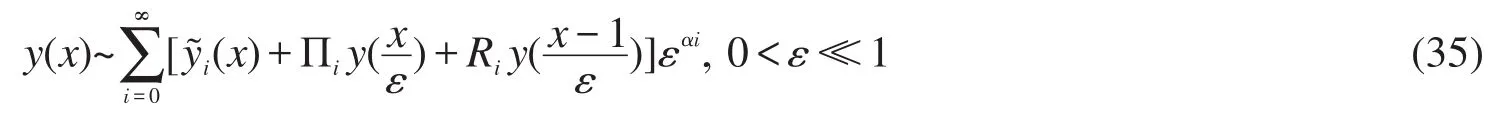
2 渐近展开式的一致有效性

定义设存在光滑函数，分别满足：

定理1在假设H1~H3的条件下，分别为2α分数阶奇摄动边值问题的上解和下解，则问题(1)~(3)存在一个解y(x,ε)，且有

证明先按以下迭代关系构造函数序列

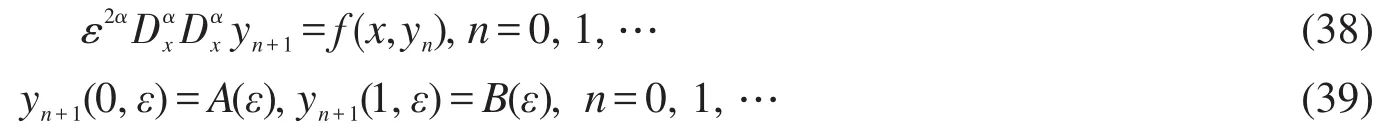
由极值原理[10]得

假设当i=n-1时，有，则

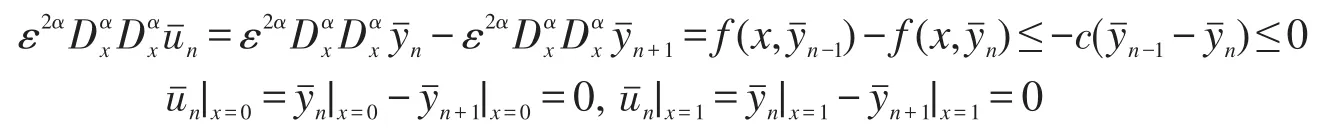
由数据归纳法知

类似可得

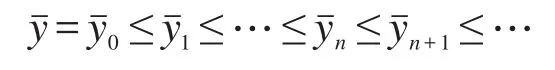
及

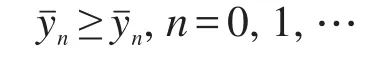
由以上讨论并结合Arzela-Ascoli定理，知2α分数阶奇摄动边值问题(1)~(3)有一个解y(x,ε)，使得

证毕。

定理2在假设HI~H3下,2α分数阶奇摄动边值问题(1)~(3)有一个解y(x,ε)，且具有如下关于ε的一致有效的渐近展开式：

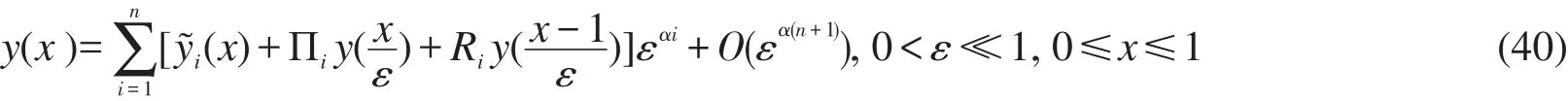
证明首先构造辅助函数a(x,ε)和b(x,ε)，

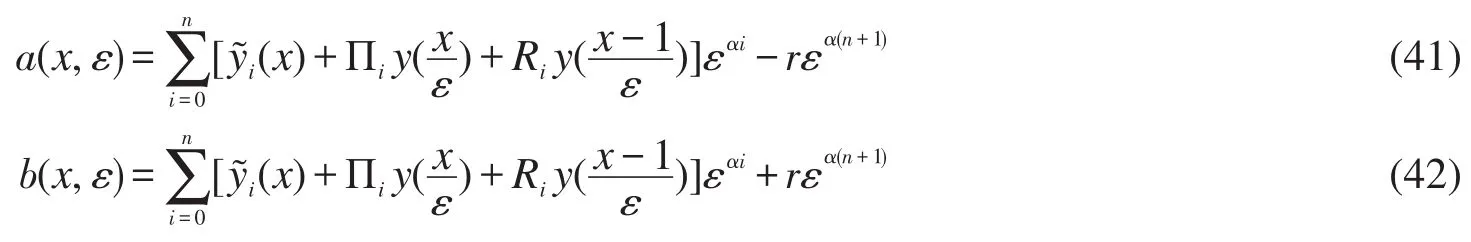
其中r为正常数，其大小在随后的证明中给出。显然，

且对于足够小的正数ε，存在一个正常数δ1，使得

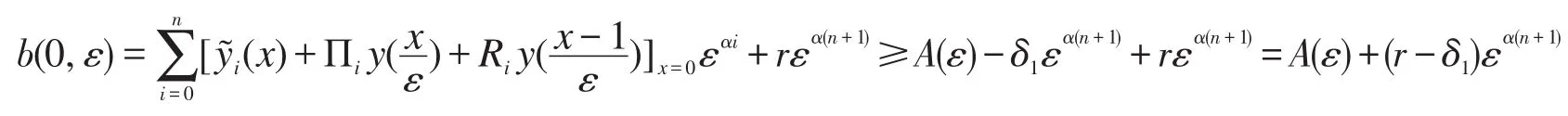
选取r≥δ1，可得

同理可得

下面证明

由假设及式(22)，(34),存在一个正常数δ2，使得

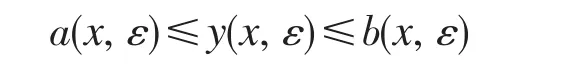
再由式(41)，(42)可知关系式(40)成立，定理2证毕。