考虑多种调节手段的配电网经济运行优化

涂辉，周建聪，石文超，高红均，李响，廖丽娟，吕林

(1．国网四川省电力公司资阳供电公司，四川省资阳市 641300；2．四川大学电气信息学院，成都市 610065)

0 引 言

在传统配电网中，由于用户不参与有功调度，只是被动地接受电能，其优化运行主要以降低总网损为目标[1-4]。然而近年来随着分布式发电(distributed generation, DG)不断发展和接入到配电网中，有关清洁能源消纳、弃风、弃光、有功-无功协调优化等决策目标是亟待考虑的问题。因此，如何协调配电网区域内的多种调节手段，实现配电网的协调优化运行，具有重要的现实意义[5-8]。

目前大量文献对配电网有功优化和无功优化分析都是将两者分别进行优化研究。实际上，不同于输电网，配电线路的电阻和电抗值较为接近，有功功率和无功功率具有强耦合关系，因此传统的有功与无功分别独立优化研究存在一定的片面性。通过配电网中的多种调节手段，采用有功-无功协调优化策略，以提高清洁能源利用率、提高配电网的运行效益、实现经济运行是配电网的一个重要命题。由于有载调压变压器(on-load tap changer，OLTC)、分组投切电容器(capacitor banks，CB)和开关等设备属于离散调节设备，而静止无功补偿器(static var compensator，SVC)等属于连续调节设备，因此优化模型必然包含离散变量和连续变量，因此该类优化问题是混合整数非线性规划(mixed integer nonlinear programming，MINLP)问题，传统的智能算法在求解该类问题时有无法获得全局最优解、求解速度慢等缺点[9-10]。因此新型的数值算法如二阶锥松弛(second order conic relaxation，SOCR)等已成为众多学者的关注热点。文献[11]建立三相Distflow潮流模型，并将其转化为混合整数二阶锥规划模型，以多时段网损最小为目标函数进行有功-无功协调优化。文献[12]构建了含有OLTC的最优潮流模型，其中将OLTC进行分段线性化建模，应用二阶锥松弛技术求解该模型。文献[13]建立了基于二阶锥规划的主动配电网动态最优潮流模型，对各主动管理元素进行线性化处理，并通过配电网络重构、综合负荷等实例验证了该模型的有效性。文献[11-13]的算例仿真表明，SOCR是一种有效求解MINLP的方法。

由于清洁能源发电的不确定性，在实际运行中，其接入必然会给配电网的运行带来一定的不确定性[14-19]。另外，部分调节手段如OLTC和CB等由于其自身调节特性，不能及时地响应系统不确定性带来的变化，并且因为其每日调节次数的限制，不能快速实时地响应负荷变化造成的电压及无功波动，因此其决策计划需根据日前负荷预测制定的调度计划确定。基于以上分析，考虑OLTC、CB、SVC、储能系统(electrical storage system，ESS)、开关[20]等多种调节手段和风机、光伏以及负荷的不确定性，提出配电网鲁棒协调优化方法，建立支路潮流模型(branch flow model，BFM)，采用SOCR技术将原非线性有功-无功协调优化模型转化为混合整数二阶锥规划(mixed integer second order conic programming，MISOCP)模型。然后，构建两阶段鲁棒优化模型，将OLTC、CB、ESS和开关等需根据日前调度计划确定的运行设备视为第一阶段变量，将SVC等能及时响应系统不确定性带来的变化的设备视为第二阶段变量，其可以在不确定参数实现后确定。最后，采用列与约束生成(column-and-constraint generation，CCG)算法求解两阶段鲁棒优化模型。

1 配电网的支路最优潮流调度优化模型

1.1 配电网基本结构

配电网稳态均以辐射状运行，其示意图如图1所示。在该辐射型配电网中，集合δ(j)表示以节点j为首端节点的所有支路的末端节点的集合，集合π(j)表示以节点j为末端节点的所有支路的首端节点的集合，箭头方向代表功率流向，ij规定了配电网潮流的正方向，即从节点i流向节点j。

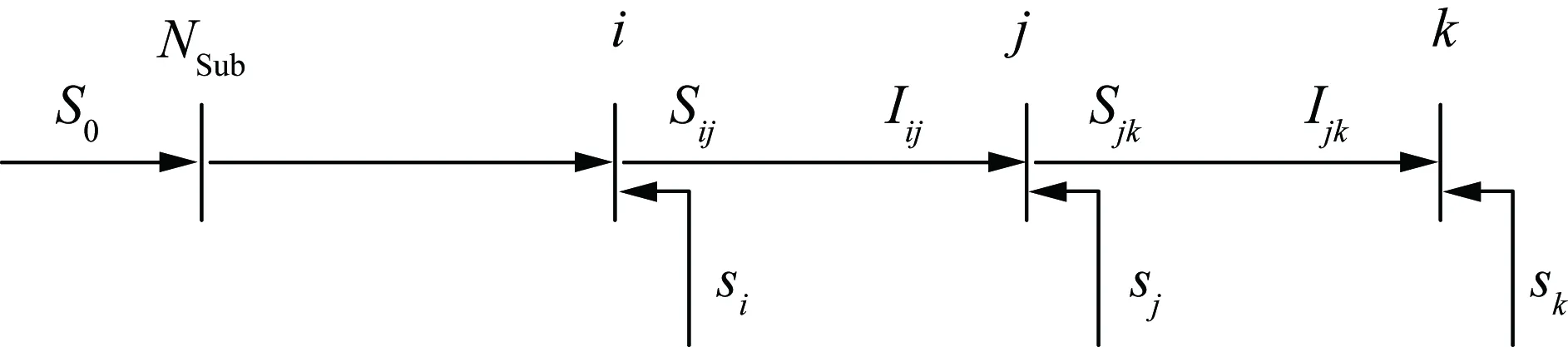
图1 辐射型配电网示意图Fig.1 Diagram of radial distribution network

图1中，节点NSub表示配电网中的变电站节点；Sij表示支路ij上从节点i流向节点j的复功率，Sij=Pij+jQij；sj表示向节点j注入的复功率，sj=pj+jqj；支路ij的复阻抗Zij=rij+jxij。假设配电网中变电站数量为Nsub个，节点数量为Nbus个，支路有Nline条。

1.2 配电网的支路潮流模型

考虑2类分布式电源，风力发电(wind turbine，WT)和光伏发电(photovoltaic，PV)，及调节手段(OLTC、CB、SVC、ESS和开关)，建立支路潮流模型如下：

(1)

Uj,t2=Ui,t2-2(Pij,trij+Qij,txij)+
Iij,t2(rij2+xij2),∀t,∀ij∈E

(2)

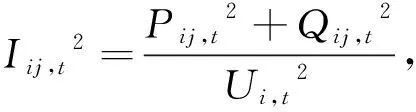
(3)

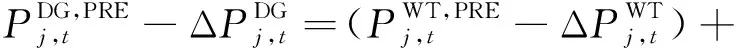
(4)

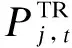
显然，该支路潮流模型式(1)—(4)为非线性规划模型，现采用SOCR方法对其进行转化，并令：

得：

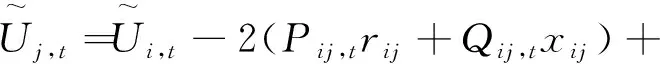
(7)

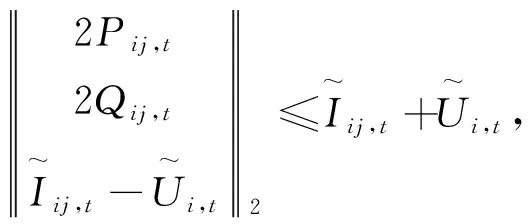
(8)

式(4)、(6)—(8)即为SOCR后的配电网支路潮流模型。这里，对SOCR的原理进行一个直观描述。如图2所示，Sorig表示原非线性规划模型的可行域，经过SOCR转化后，原问题的可行域变为一个新的可行域SSOCR，并且该新可行域SSOCR是一个凸可行域。显然SOCR技术扩大了原问题可行域，如果通过凸可行域SSOCR求得的解在原可行域Sorig中，则不等式(8)与等式(3)完全等价，提高了问题的求解速度。

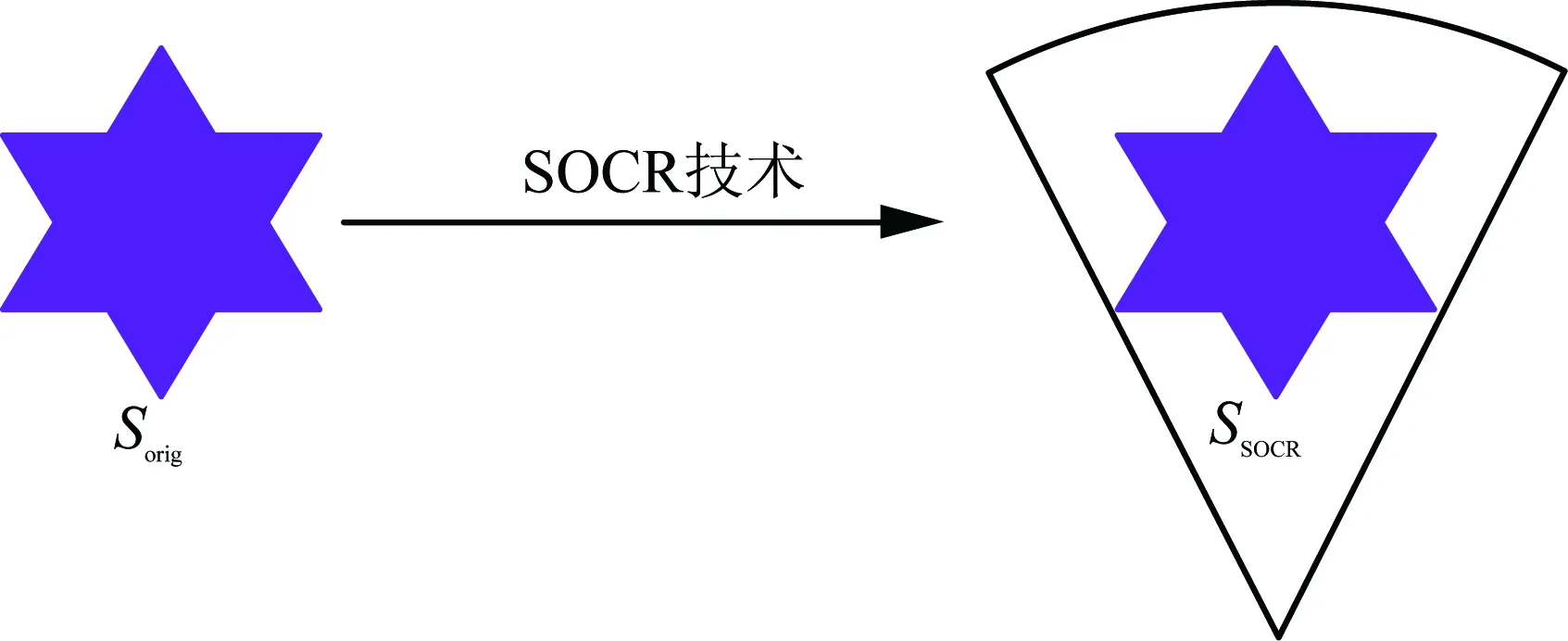
图2 SOCR可行域简要描述Fig.2 Brief description of the SOCR feasible region

1.3 配电网经济运行数学模型

在配电网环境中，主要调节方式有：(1)OLTC档位调节；(2)主要通过CB、SVC等手段进行无功补偿调节；(3)通过ESS、DG进行有功功率调节；(4)通过开关重构对网络进行有功无功潮流重新分布。因此本小节介绍的配电网经济运行数学模型以运行成本C最小为目标函数，并包括多种调节手段的相关调节约束和1.2节所描述的支路潮流模型约束。

1.3.1目标函数

本文的配电网经济运行数学模型的目标函数包括配电网总网损成本CLoss、主网购电成本CTR和弃风、弃光成本CWT、CPV。

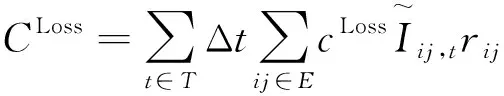
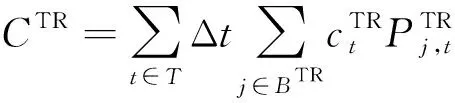
(11)

(12)

式中cLoss、cTR、cWT、cPV分别表示配电网网损、主网购电、弃风和弃光的单位成本。

目标函数可表示为

minC=CLoss+CTR+CWT+CPV=

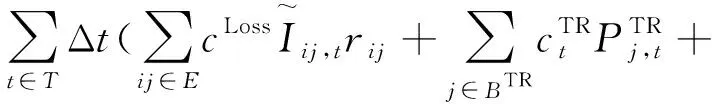
1.3.2约束条件

(1)有载调压变压器约束。

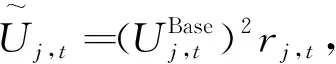
(14)

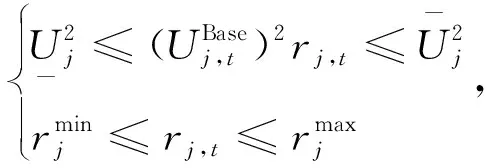
(15)

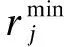
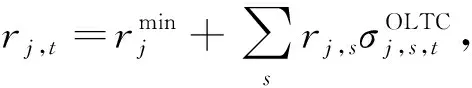
(16)

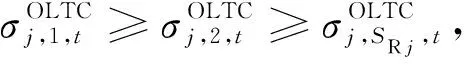
(17)

(18)

∀t,∀j∈BOLTC

(19)

∀t,∀j∈BOLTC

(20)

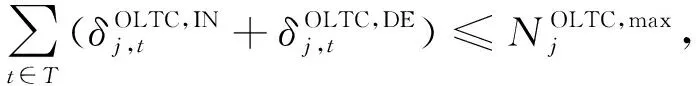
(21)

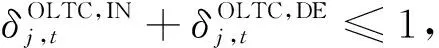
(22)

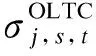
(2)分组投切电容器约束。

本文所考虑的分组投切电容器补偿容量与节点电压无关，每组补偿容量为常数，总补偿容量仅与其投入组数成正比。显然CB补偿容量为离散变量，相应的约束条件如下：

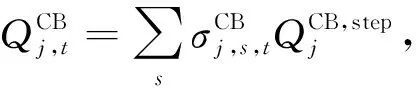
(23)

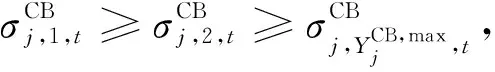
(24)

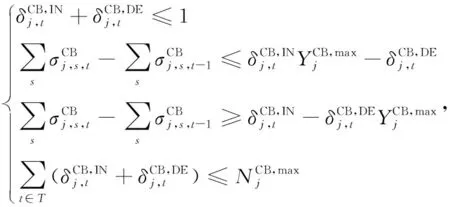
(25)

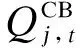
(3)静止无功补偿器约束。

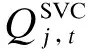
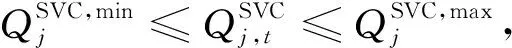
(26)

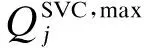
(4)储能系统约束[21]。

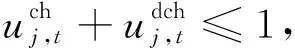
(27)

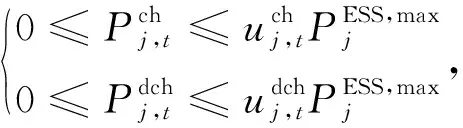
(28)

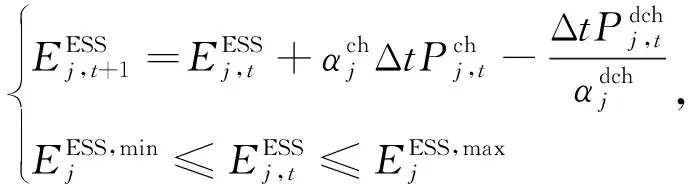
(29)

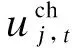
(5)开关重构约束。

配电网开关重构是配电网经济运行的重要组成部分。在支路潮流模型中，Pij实际上已经表示了潮流的正方向，Pij>0表示支路潮流从i节点流向j节点，Pij<0表示支路潮流从j节点流向i节点。建立开关重构约束如下：

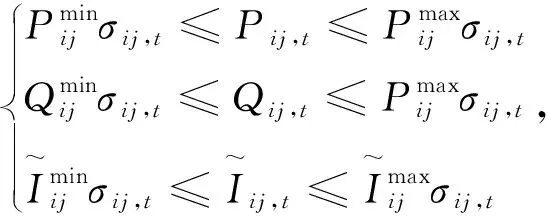
(30)

∀j∈B,∀ij∈E

(32)

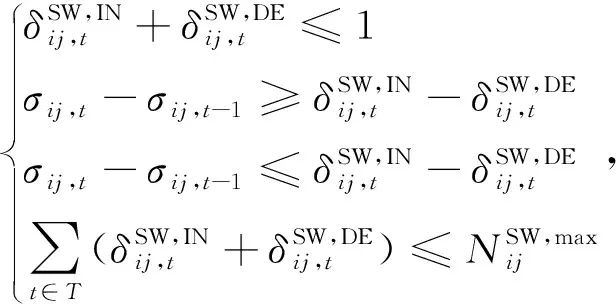
(33)

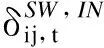
(6)主网出力约束。

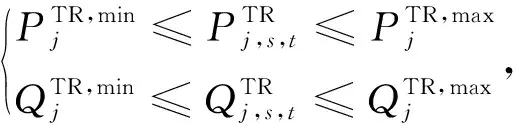
(34)

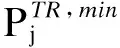
(7)风力发电与光伏发电约束。

(8)配电网安全运行约束。

(36)

综上，式(13)、(15)—(36)和SOCR后的配电网支路潮流模型式(4)、(6)—(8)构成本文的配电网经济运行数学模型。

2 两阶段鲁棒协调优化模型

2.1 确定性数学模型

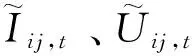
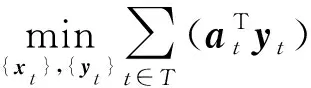
s.t.xt∈Xt,∀t

(38)

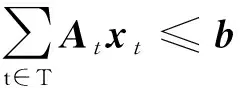
Mtyt≤ft,∀t

(40)

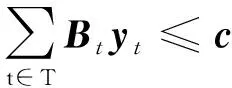
Dtxt+Ftyt=Gtdt+Htgt,∀t

(42)

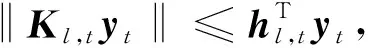
(43)

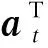
2.2 两阶段鲁棒协调优化模型

2.1节所述的矩阵形式的配电网经济运行数学模型是确定性模型。但是有清洁能源接入的情况下，系统会存在较多的不确定性，主要包括风机、光伏出力的不确定性和用户负荷的不确定性。考虑清洁能源出力的不确定性，本文采用区间鲁棒优化方法，确定使用各种不确定运行状态的鲁棒优化运行方案。其数学模型如下：

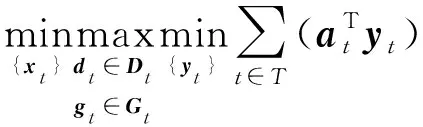
(45)

在上述模型中，内层max-min模型的意义是在各种不确定性变量变化的范围内，确定使总运行成本最大的最恶劣场景。第一阶段变量{xt}根据日前调度计划确定，然后通过网络的最优潮流解得出第二阶段变量{yt}的最优解。模型的基本原理是确定系统运行在最恶劣状态下总运行成本最小的鲁棒优化方案。根据两阶段鲁棒优化模型的特点，式(44)、(45)可表示为如下形式：

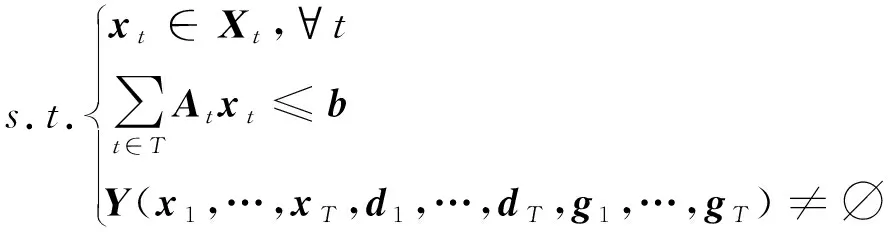
其中：

(49)

综上，式(46)—(49)即两阶段鲁棒协调优化模型。

3 求解算法

上述两阶段鲁棒优化模型实质上是min-max-min问题。对于该类多层模型常用分解算法进行求解，例如Benders分解算法、对偶割平面算法和CCG算法[22]。而采用遗传算法[23]、粒子群算法[24]等智能算法求解多层模型时，容易出现求解速度较慢、收敛性差、陷入局部最优等问题。相比智能算法和其他分解算法，CCG算法有收敛性好[25]、求解速度快、保证全局最优等优点。因此本文采用CCG算法将两阶段鲁棒优化模型分为主问题和子问题进行求解。CCG子问题的求解主要是通过对内层max-min模型的min模型进行对偶转化，得到单层的max模型进行求解。CCG算法通过子问题寻找最恶劣场景，然后加入到主问题中，并进行反复迭代求解。

3.1 两阶段鲁棒优化模型的CCG求解算法

3.1.1CCG主问题

CCG主问题是在生成的最恶劣场景下求解满足约束条件式(47)的最优解，该最优解为两阶段鲁棒优化模型提供一个下界值。

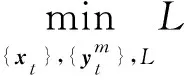
s.t.xt∈Xt,∀t

(51)

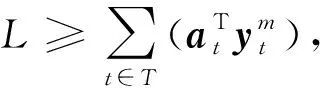
(52)

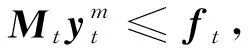
(53)

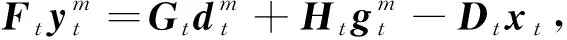
(54)

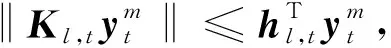
(55)

3.1.2CCG子问题

当第一阶段变量已知时，通过CCG算法寻找到最恶劣场景，加入到主问题中进行反复迭代，求解子问题的结果为两阶段鲁棒优化的数学模型式(44)、(45)提供一个上界值。

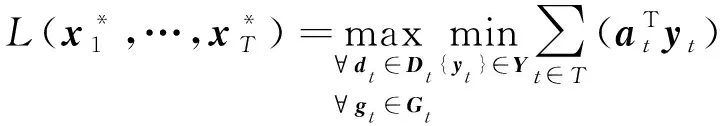
利用对偶原理，将双层max-min模型转化为单层max模型如下：

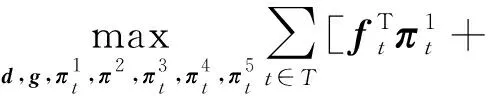
(58)

(59)

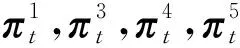
3.2 两阶段鲁棒协调优化求解流程图

两阶段鲁棒协调优化求解流程如图3所示。图中LB表示下界值，UB表示上界值，ε为给定的收敛精度。

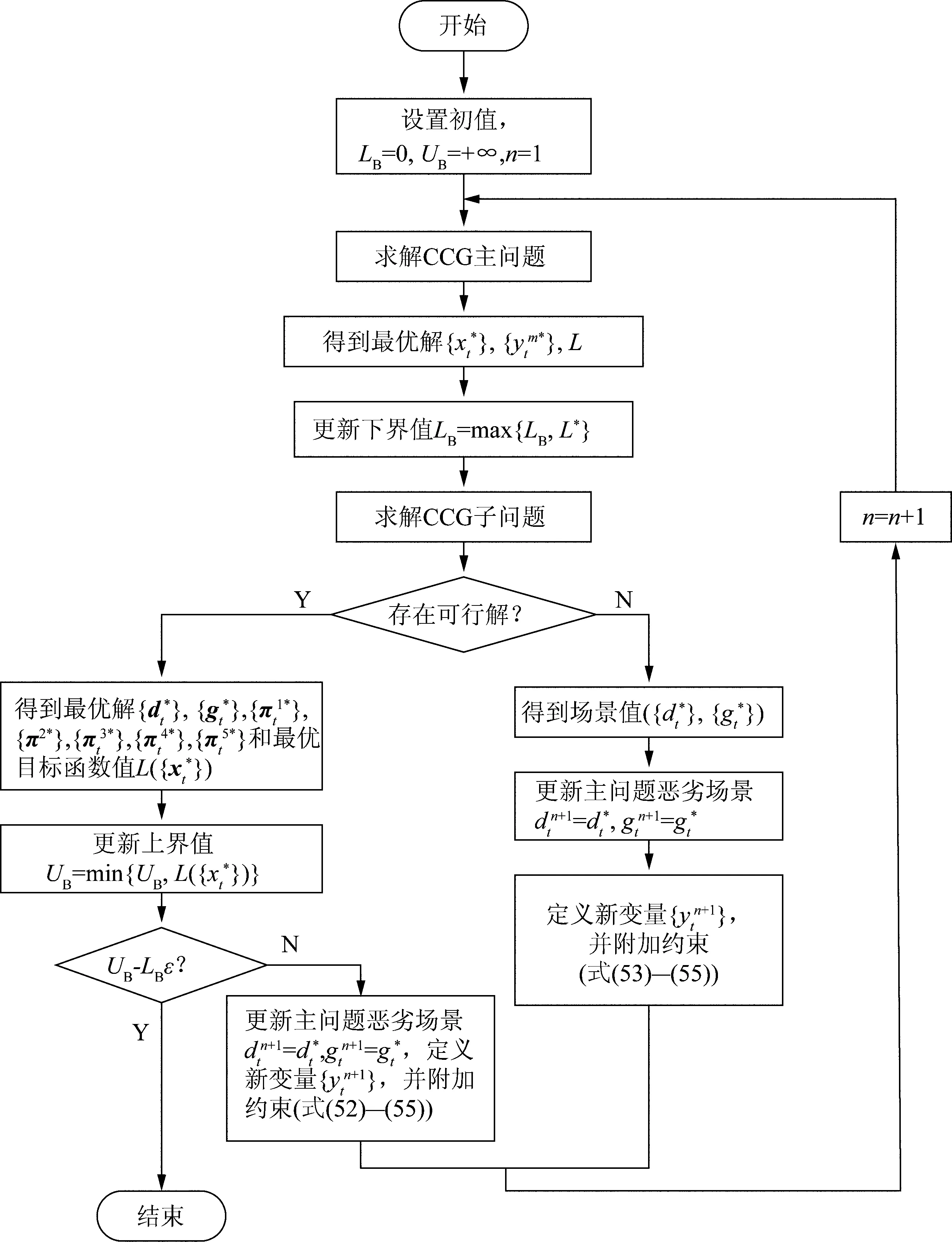
图3 两阶段鲁棒协调优化求解流程图Fig.3 Flowchart of two-stage robust coordination optimization solution

4 算例分析

4.1 算例基本数据及运行环境

本文采用IEEE 33节点算例对本文提出的模型进行计算、分析。系统基准容量SBase=1 MV·A，基准电压UBase=10 kV，选取1号节点为变电站节点。OLTC、CB、SVC、ESS和开关等调节设备参数和风机、光伏的安装位置见表1—6。主网有功无功出力上下限见表7。系统总有功负荷、风机总出力、光伏总出力曲线如图4所示，网损成本为500元/(MW·h)，参考文献[26]，弃风、弃光成本为500元/(MW·h)，而其中10：00—16：00时段光伏发电达到其最大发电功率，并被系统完全消纳。系统配置为Win10 64位，i5-7200U，2.50 GHz，8 GB内存，程序在Matlab 2015b环境中基于CPLEX算法包运行。

表1OLTC参数
Table1ParametersofOLTC

表2 CB参数Table 2 Parameters of CB

表3 SVC参数Table 3 Parameters of SVC

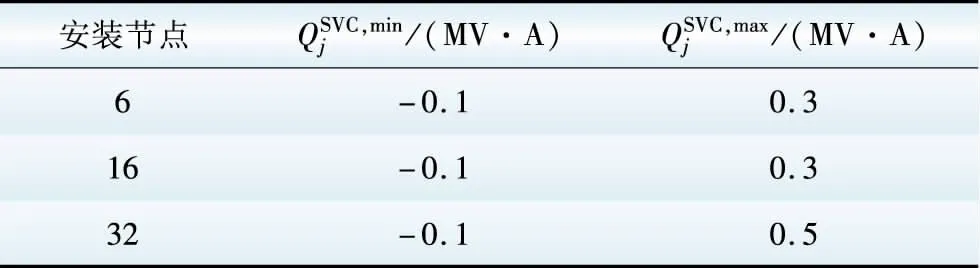
表4 开关参数Table 4 Parameters of switch

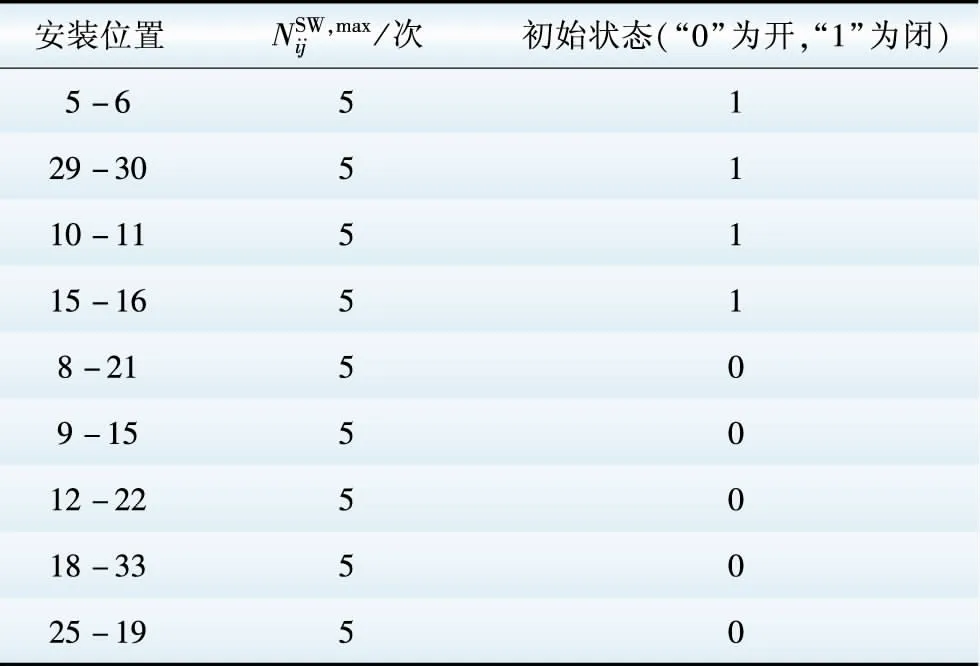
表5 风机、光伏安装节点Table 5 Nodes and capacity of WT and PV

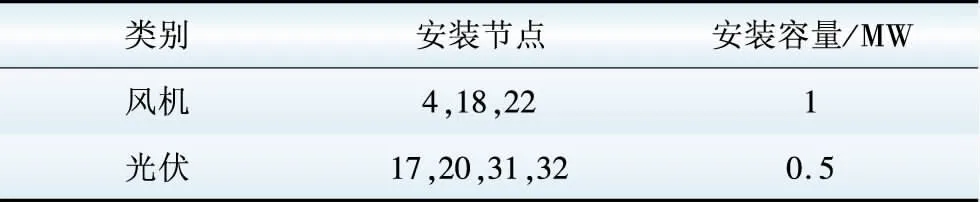
表6 ESS参数Table 6 Parameters of ESS

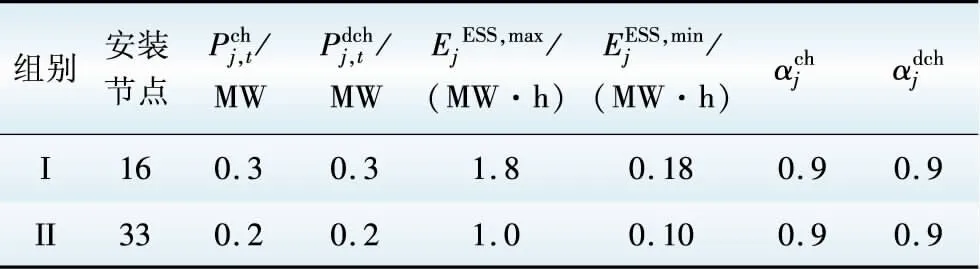
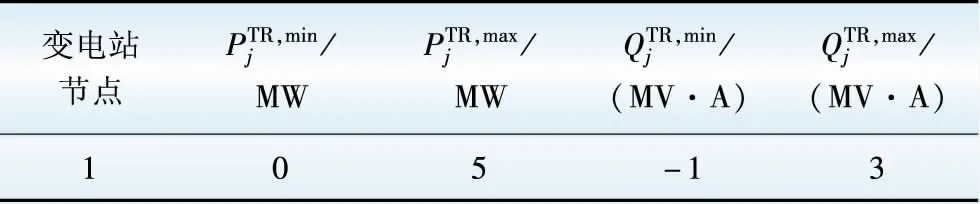
表7 主网出力参数Table 7 Parameters of transmission network output

4.2 计及开关重构的经济运行优化分析

以配电网开关重构为例，根据图4的有功负荷及DG有功出力曲线，对计及开关重构与未计及开关重构时的运行成本进行对比分析，IEEE 33节点运行结果见表8。

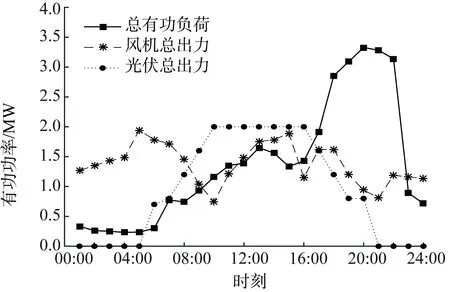
图4 总有功负荷、风机总出力、光伏总出力曲线Fig.4 Curves of total active load, total active power of WT and total active power of PV

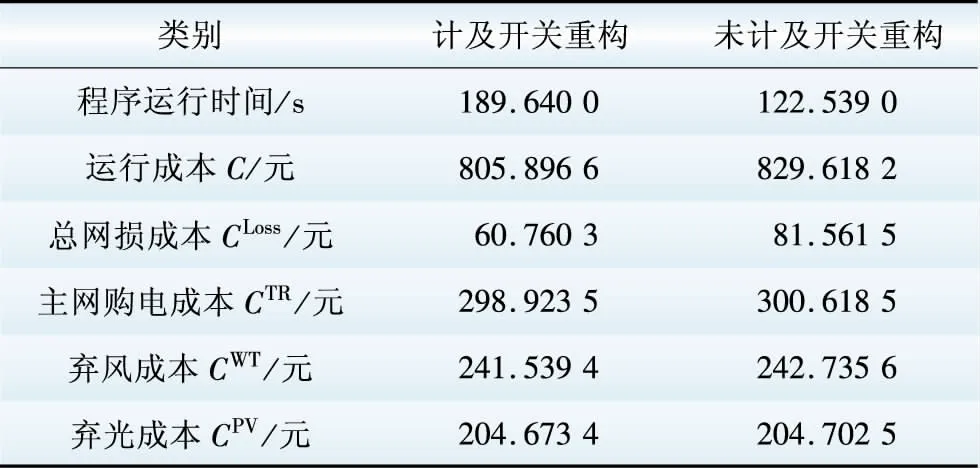
其中，未计及开关重构时的开关状态为初始状态，见表4。算例中OLTC、CB、SVC、ESS等设备同时参与调节，其中在仿真时间内计及开关重构时OLTC分接头调节次数为4，未计及开关重构时OLTC分接头调节次数为5。根据本文所构建的场景基础数据，开关重构对于清洁能源的消纳作用效果不明显，主要是对网络损耗有较大的影响，因此可以观察到表8中弃风、弃光成本变化不明显，而网损成本有较大变化。正是由于清洁能源利用变化不大，且系统内负荷一定，同时网损本身占总负荷比重较小，从而主网购电成本也不存在明显的变化，因此系统运行的总成本变化主要来自于总网损成本的变化。

计及开关重构与未计及开关重构时的储能系统充放电功率如图5、6所示。显然，在配电网经济运行中，计及开关重构时能够充分利用储能系统的充放电减少运行成本。

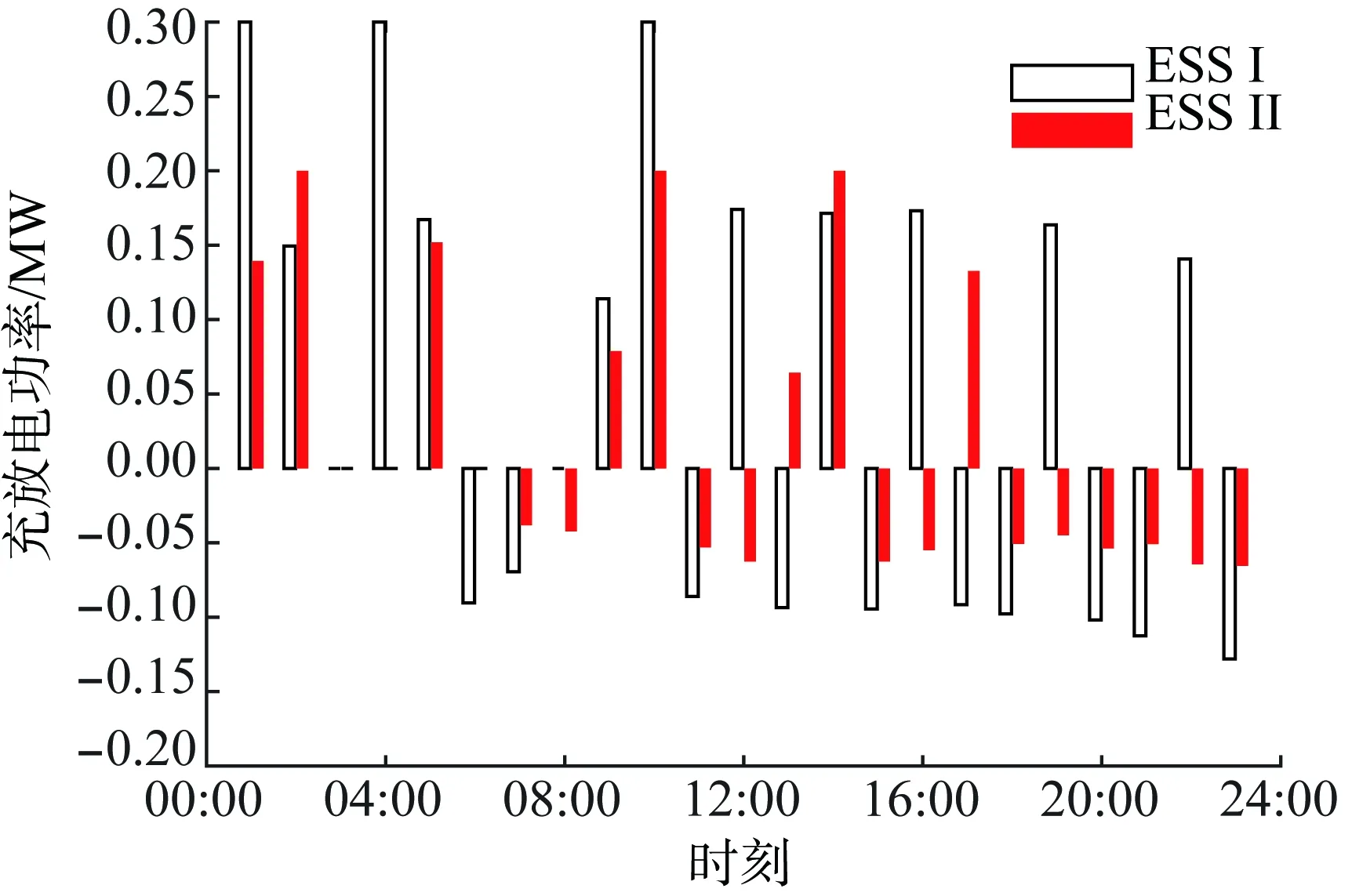
图5 计及开关重构时的储能系统充放电功率Fig.5 Charge and discharge power of ESS considering switch reconfiguration

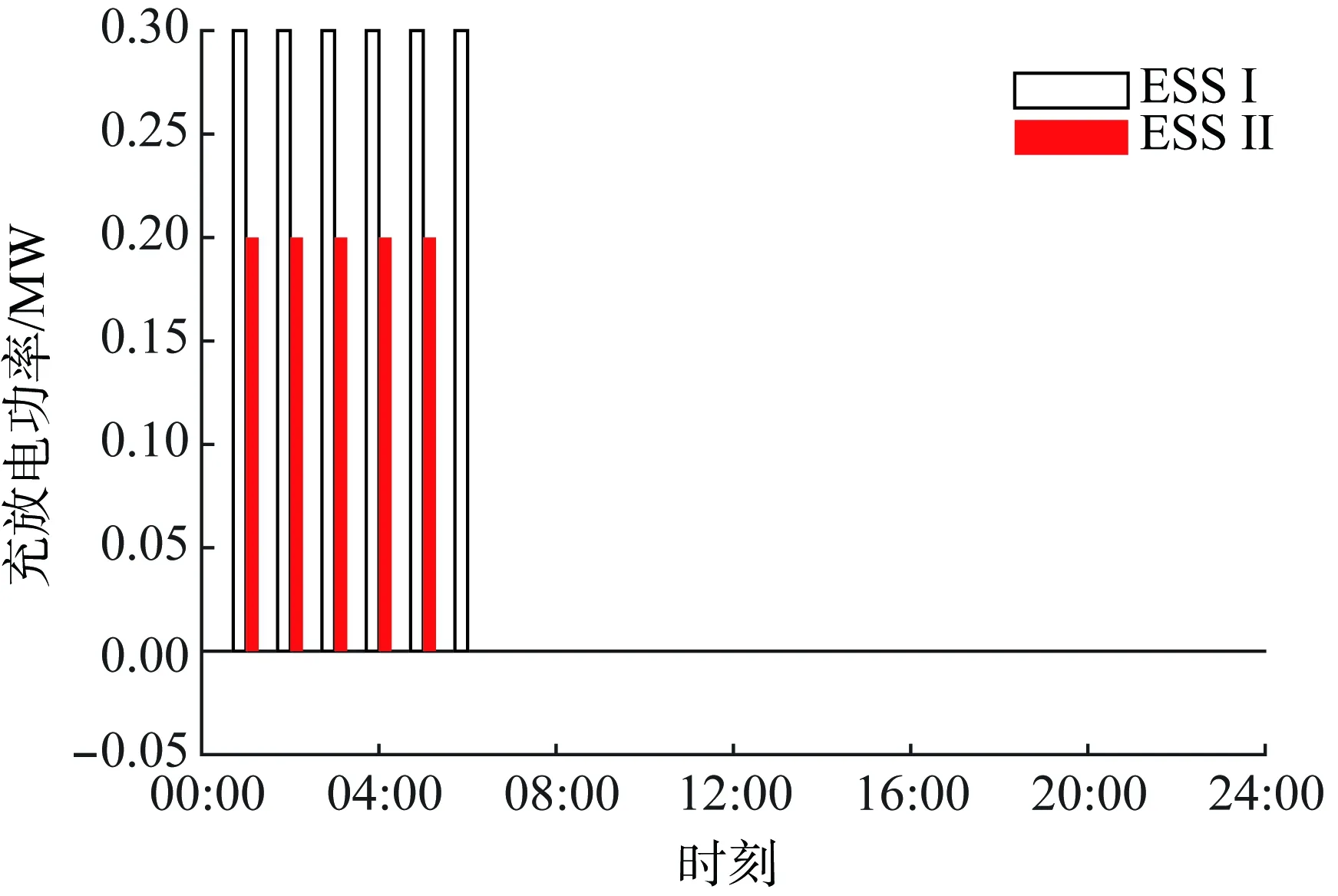
图6 未计及开关重构时的储能系统充放电功率Fig.6 Charge and discharge power of ESS without considering switch reconfiguration

因此，在配电网的鲁棒经济运行中，开关重构是一个降低网损的重要措施，并且能够充分利用储能系统减少运行成本。

4.3 确定性方法与鲁棒协调优化分析

为了分析本文所提出的鲁棒协调优化方法适应不确定性的能力，以α表征风机和光伏出力的不确定性，因此风机和光伏出力的不确定性区间为[1-α, 1+α]PWT,PRE和[1-α, 1+α]PPV,PRE，当α取值为[0.1, 0.6]时，采用蒙特卡洛方法随机生成100 000个场景进行计算，从而获得确定性方法与鲁棒协调优化方法的平均成本对比，如图7所示。显然，随着α的不断增大，应用鲁棒协调优化方法求得的成本上升趋势较确定性方法更缓慢，因此鲁棒协调优化方法比确定性方法能够更好地适应不确定性，并且该方法能够显著降低运行成本，在配电网经济运行中具有一定的实用性。

5 结 论

本文提出了一种考虑OLTC、CB、SVC、ESS和开关等多种调节手段的配电网鲁棒协调优化方法，采用SOCR技术将原非线性有功-无功协调优化模型转化为MISOCP模型，考虑风机、光伏出力和负荷的不确定性建立了两阶段鲁棒协调优化模型，并通过IEEE 33节点算例仿真，得出结论如下所述。

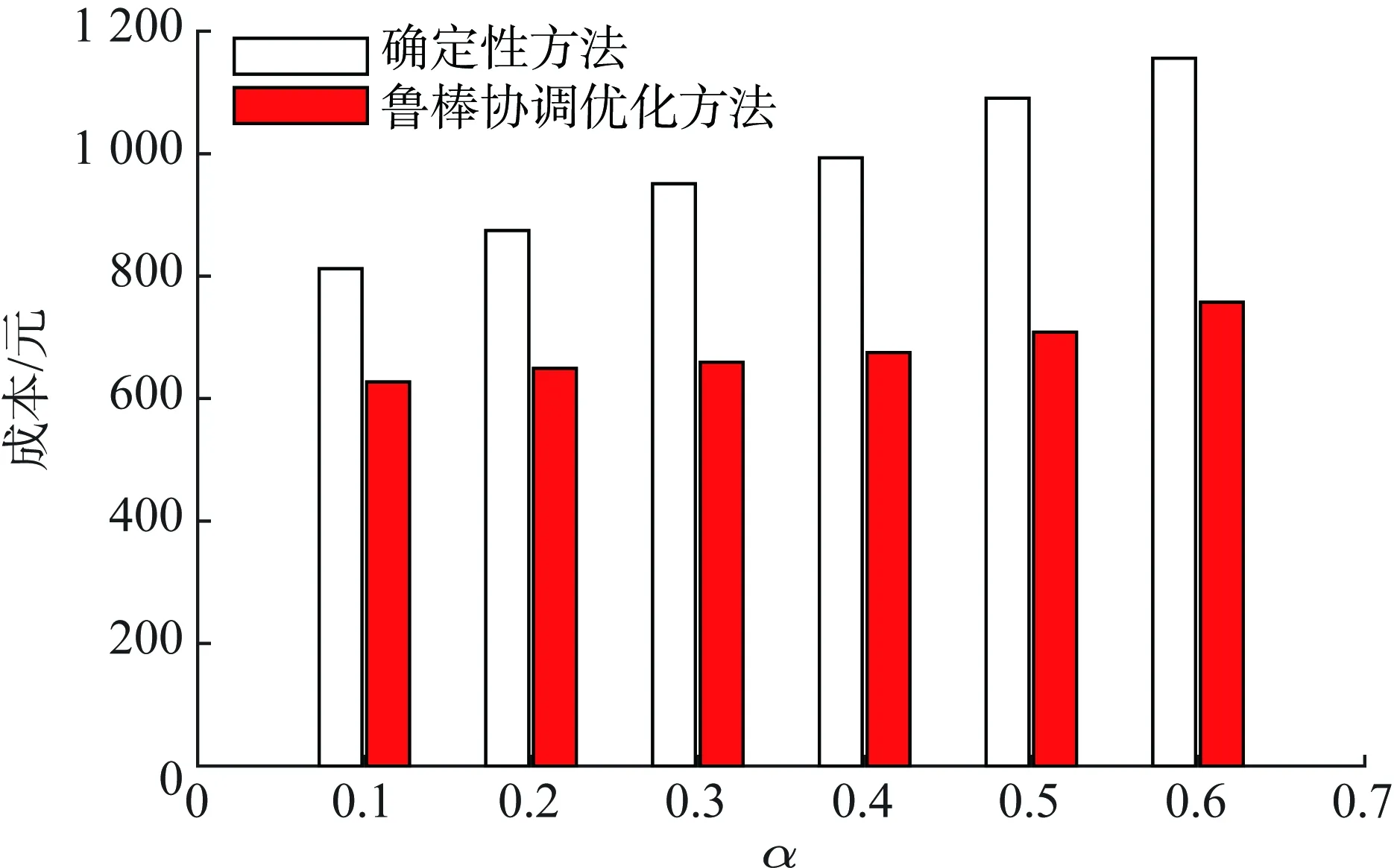
图7 确定性方法与鲁棒协调优化的成本对比Fig.7 Comparison of cost between deterministic approach and robust coordination optimization

(1)以开关重构为例，在配电网经济运行中，开关重构能够有效减少网损成本，并且能够充分利用储能系统的充放电以及OLTC、CB和SVC的调节减少总运行成本。

(2)随着α的不断增大，鲁棒协调优化方法能够更好地适应清洁能源发电的不确定性，鲁棒性更佳，可以显著降低配电网运行成本。