基于场景分析的有源配电系统有功无功协调鲁棒优化策略

黄河, 任佳依，高松，顾伟，刘海波

(1. 国网江苏省电力有限公司，南京市 210000；2. 国网江苏省电力有限公司经济技术研究院，南京市210008；3. 东南大学电气工程学院，南京市 210096)

0 引 言

随着大量分布式电源、储能、无功补偿装置等接入配电网，传统配电网正在逐步演变为具有众多可控资源的有源配电系统。不同于输电网，配电系统阻抗比较大，PQ解耦性差，传统有功无功解耦的优化方法不再适用于配电系统优化，单方面有功优化和无功优化不能充分发挥各可控资源有功无功功率在系统运行过程中的作用，无法兼顾系统在提高经济效益和保证安稳运行两方面的要求。因此，近年来，不少学者开始研究基于有功无功协调的有源配电系统优化方法。

文献[1-2]将有源配电系统的优化分为2个阶段，第1阶段为有功功率优化，第2阶段为实时无功功率优化，但该方法其实是有功优化和无功优化交替进行的过程，其在实质上仍未考虑系统中有功功率和无功功率的强耦合特性。文献[3-4]将可调资源的有功无功出力以盒式约束的形式加入到优化模型中，即以区间约束形式分别表示有功出力和无功出力的范围，但可调资源的功率特性受到多种因素的影响，采用盒式约束容易使其运行点超出功率极限，不符合工程实际。因此，最为可行的方法是将可调资源的有功无功功率极限方程作为约束加入到优化模型中[5-8]，但该类模型通常为非凸非线性优化问题，在求解上存在一定难度。文献[7-8] 提出了基于凸松弛方法的有功无功协调优化模型，实现了原始问题的高效求解和全局寻优。总体而言，有源配电系统有功无功协调优化相较单方面的有功/无功优化，其控制变量更为多样，优化模型更为复杂，求解过程更为困难。

另一方面，上述有源配电系统有功无功协调优化模型，皆是基于可再生能源出力和负荷预测信息进行确定性优化调控决策，并未考虑功率波动不确定性和预测误差对决策的影响。在有源配电系统的实际运行过程中，通常实时量测不足，对于负荷预测通常是基于伪量测数据经过状态估计得出，误差较大[9]。另一方面，系统中的部分可再生能源如风电、光伏等，受外界环境因素的影响，其出力具有随机性和间歇性，使得按确定性优化策略求得的调控计划与系统实际的运行情况存在较大偏差，导致确定性优化调控决策并不能完全保证系统实际运行安全性的情况。在预测误差较大的情况下，确定性优化调控策略下仍有可能出现电压幅值越限等实际运行安全问题，降低了调控的可靠性。因此，如何在保证系统安全经济运行的同时兼顾可再生能源出力以及负荷波动不确定性对系统运行的影响，是有源配电系统优化研究中亟待解决的课题。当前电力系统中对不确定性处理方法有概率论方法、区间分析方法和鲁棒优化等[10-11]。其中，鲁棒优化的核心在于制定恶劣场景下的决策方案，具有计算量较小等优点，故可以用于考虑功率不确定的有源配电系统有功无功协调优化研究中。

本文提出一种基于场景分析的有源配电系统有功无功协调鲁棒优化策略。首先将可再生能源以及储能的有功无功功率极限考虑到有源配电系统的优化中，结合电力有载调压器(on load tap changing，OLTC)、电容器等传统无功设备，建立较为全面的基于二阶锥优化的有源配电系统确定性有功无功协调优化模型，然后基于场景分析法寻找系统运行过程中可能出现的最恶劣情况，并求得其对应的有功无功协调鲁棒优化调控策略，所求得的策略能有效降低功率波动时系统出现安全性问题的几率。通过修改后的IEEE 14节点配电系统验证本文所提方法在保证系统安全稳定运行方面的有效性和优越性，以及鲁棒优化策略在应对功率波动不确定性方面的有效性。

1 有源配电系统确定性有功无功协调优化模型

针对含风电、光伏、储能、电力有载调压器以及电容器等有功无功可调资源的有源配电系统，可建立其日前多时段有功无功协调优化模型。模型中的控制变量包括风电安排的有功出力和无功出力，光伏安排的有功出力和无功出力，储能的有功无功出力以及电力有载调压器和电容器的档位。

1.1 优化目标

有源配电系统日前有功无功协调优化以日前系统有功网络损耗最小作为目标函数，同时，根据我国大力推行新能源发电的政策，应尽量避免出现弃风、弃光等可再生能源浪费的现象，仅在严重影响系统安全稳定运行时适当削减部分可再生能源功率，故将可再生能源有功功率的削减量作为惩罚项纳入到优化目标中：

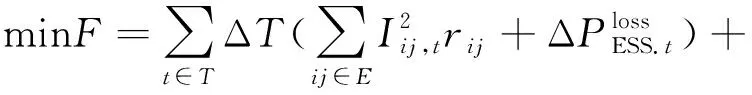
(1)

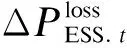
1.2 约束条件

模型约束主要包括潮流约束、运行安全约束和可控资源有功无功出力约束。

1.2.1潮流约束

对于辐射状配电网中的某一支路ij，采用支路潮流模型[12]表达电压电流与功率的关系：

(2)

式中：Pij,t和Qij,t分别为t时刻节点i流向节点j的有功功率和无功功率；Vi,t为节点i的电压幅值；xij为支路ij的电抗；k:(j,k)表示以节点j为首节点的末端节点集合；Pj,t和Qj,t分别为节点j处的有功注入功率和无功注入功率，可表征如下：

(5)

(6)

1.2.2系统运行安全约束

系统运行安全约束包括节点电压约束和支路电流约束：

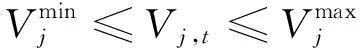
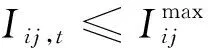
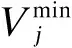
1.2.3可控资源有功无功出力约束

可控资源有功无功出力约束包括光伏有功无功出力约束、风电有功无功出力约束、储能有功无功出力约束、电力有载调压器约束以及电容器运行约束。

(1)光伏有功无功功率极限约束。光伏发电设备通常采用逆变器并网，通过逆变器的复用技术产生无功功率[13]，其有功无功出力约束受逆变器最大视在功率限制：

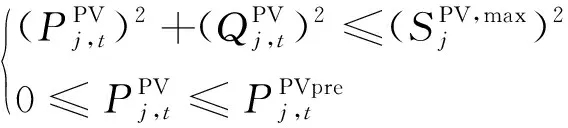
(9)

(2)风电有功无功功率极限约束。风力发电通常经双馈感应发电机(doubly fed induction generator, DFIG)并网， DFIG可通过调节励磁电流幅值、励磁频率以及相位来调节风电的有功功率和无功功率[14]，其有功无功出力受定子绕组最大电流限制和转子侧变换器最大电流限制：

(10)

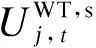
(3)储能有功无功功率极限约束。储能系统通过基于脉宽调制(pulse width modulation，PWM)技术的电压源型逆变器——能量转换系统(power conversion system，PCS)[15]接入配电网。PCS系统可以实现储能有功功率和无功功率的解耦控制，其有功无功出力极限受所接PCS系统的最大视在功率限制。此外，储能系统不能同时运行在充电和放电状态，因此通常在对其进行建模时，引入0-1变量来保证不会出现既充电又放电的物理不可行情况：

为了保证储能系统工作效率，延长其使用寿命，其在可存储电量的容量上必然有一定的限制：

(12)

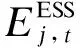
t时段储能充放电能量损耗则可表示为

(13)

(4)电力有载调压器运行约束。OLTC是配电网中重要的无功调节设备，对包含有电力有载调压器的配电网线路ij，设其在t时刻节点i处电压与节点j处电压的变比为kij,t∶1，则kij,t可建模如下:

(14)

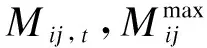
则对含OLTC的支路，其潮流约束公式(3)修改为

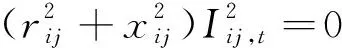
(15)

式中ΩOLTC为系统中接入OLTC的支路集合。

(5)电容器运行约束。

电容器通过改变其投切档位来调整其对于系统的无功补偿量，其运行约束为

(16)

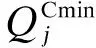
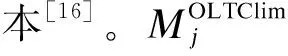
综上，有源配电系统确定性有功无功协调优化模型可表述如下：

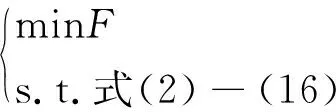
1.3 模型的非凸非线性处理

可以看到，有源配电系统确定性有功无功协调优化模型是一个多决策变量非凸非线性混合整数规划模型，直接对其求解存在一定难度，且不能保证解的全局最优性。模型中的非凸性主要体现在OLTC运行约束式(15)和潮流约束式(2)—(4)。对于OLTC运行约束，本文采用分段线性化方法对式(15)进行了线性化处理[17]。而对于潮流约束式(2)—(4),本文则采用凸松弛的方法，将原潮流方程转化为标准的二阶锥形式，步骤如下：

引入新变量vi,t和iij,t，其定义分别表示如下：

(18)

将式(18)代入模型(2)—(4)中，并对式(4)进行凸松弛处理[18]，可将模型转化为

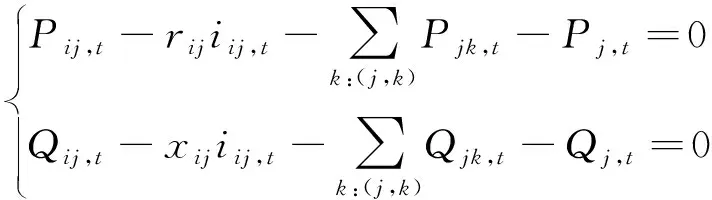
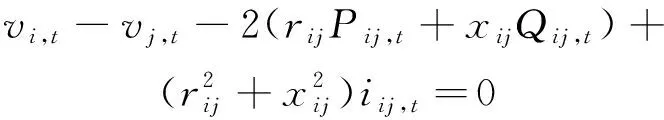
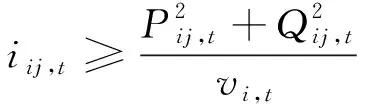
对式(21)做进一步等价变形，可转化为标准二阶锥形式：

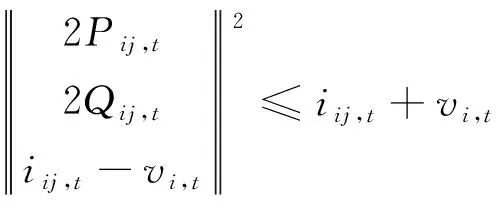
经过上述处理后，原模型转化为含混合整数变量的二阶锥优化问题，可采用凸优化方法，在求解过程中避免陷入局部最优等问题，且保证较高的精度和计算效率。

2 基于有功无功协调的鲁棒优化策略

2.1 考虑不确定性的有源配电系统有功无功协调优化模型

有源配电系统运行过程中，存在的不确定因素主要有2类：可再生能源出力(在本文中主要为风电和光伏)和负荷波动，以不确定集形式可表示为

(23)

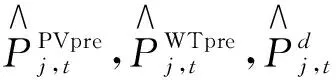
(24)

定义有源配电系统有功无功协调优化模型中的控制变量集合为x，状态变量集合为y，则经过凸松弛处理后的式(17)模型又可表示为如式(25)所示的紧凑表达形式：

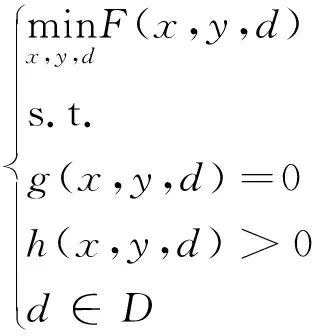
式中：g(x,y,d)=0表征模型中的等式约束；h(x,y,d)>0表征模型中不等式约束。

为应对不确定性对优化调控决策的影响，较为有效的方法是寻找最恶劣的情况，使决策方案在该最恶劣情况下依然能够保证系统运行的要求[19]，在本文中，功率不确定性以及预测误差对优化调控决策的影响主要体现在可能导致实际调控过程中出现电压越限等安全性问题的情况，故定义最恶劣情况为电压偏差最大的情况，即：

(26)

考虑不确定性因素和预测误差的有源配电系统有功无功协调优化模型可拆分为两层优化问题：外层主问题为在给定功率波动d*情况下求解使目标函数值最小的优化调控策略；内层子问题为在给定调控策略x*时求解使电压偏差最大，即情况最恶劣的功率波动情况d。两层优化问题之间的关系如图1所示。

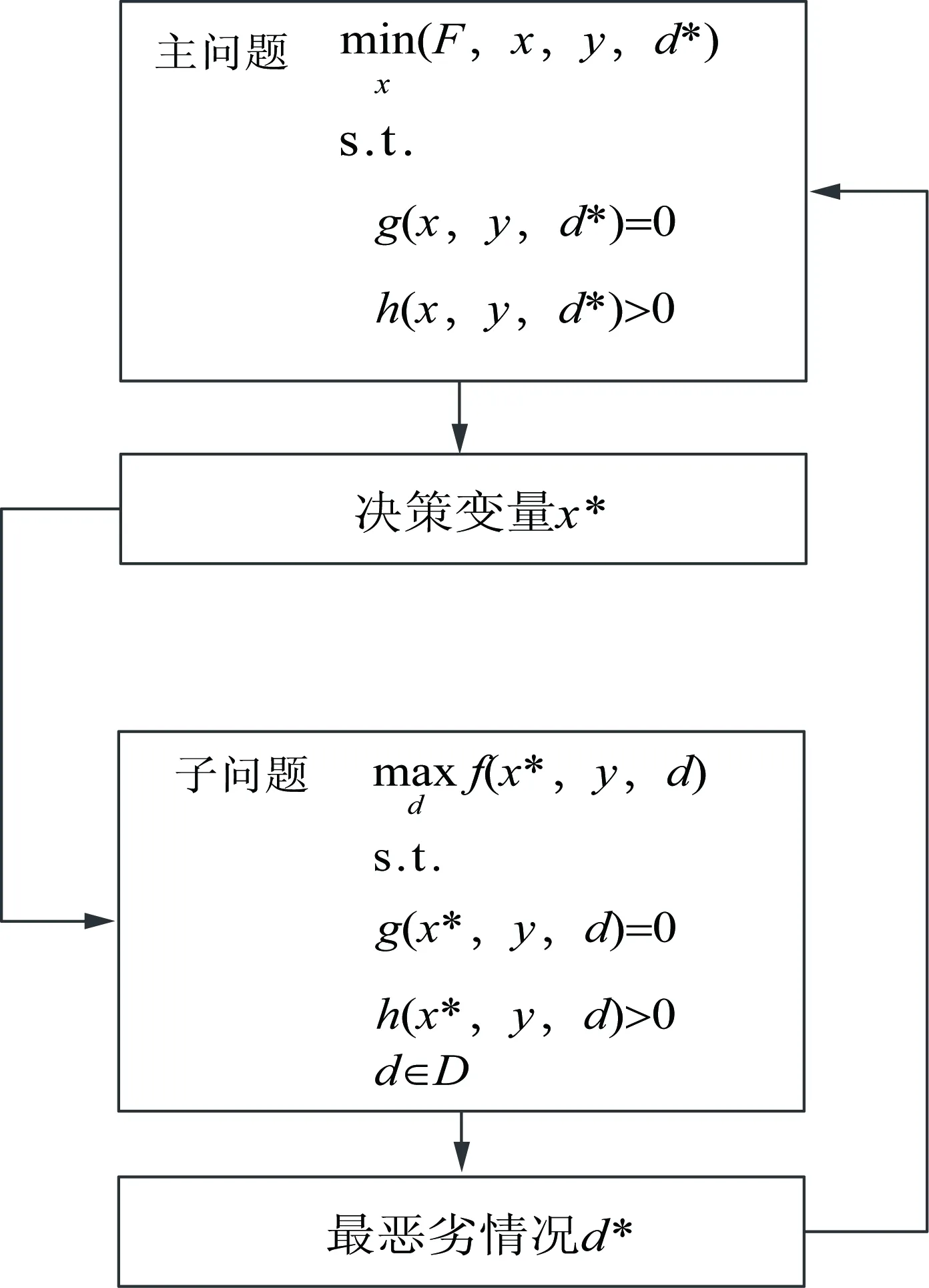
图1 考虑不确定性的有源配电系统有功无功协调优化Fig.1 Coordinated optimization of active and reactive power in active distribution system considering uncertainties

对于上述考虑功率不确定性的有源配电系统有功无功协调优化模型，本文考虑采用基于场景分析法的优化策略来进行求解。

2.2 基于场景分析法的鲁棒优化求解策略

有源配电系统中功率波动不确定性集中体现在不确定集D中，通常采用概率密度函数的形式表达，对于风电、光伏以及负荷预测不确定性概率密度函数，通常根据大量历史数据分析统计得到。但概率密度函数是连续函数，基于其来进行优化求解较为困难，将概率密度函数曲线进行离散化是一种较为合理而有效的解决办法，即生成足够多的场景来近似表示概率密度，这些场景构成了表征有源配电系统功率波动不确定性的场景集，2.1节中的求解策略即可等效为在场景集中寻找恶劣场景。

以离散场景叠加构成较为庞大的场景空间，可较为准确地表征不确定集D，但若直接对其中的所有场景进行有功无功协调优化求解，则受计算复杂度和计算量的限制，无法快速寻找到最恶劣场景下的优化解。因此，还需要对原始场景集中的场景进行削减，以生成能很好近似概率密度函数的典型场景集合，减少优化求解计算量。

2.2.1场景生成

对于表征不确定集D的原始场景集的生成，需要保证所生成的场景集能够覆盖不确定集的整个样本空间，才能够准确反映功率波动的概率分布特性。因此，本文采用拉丁超立方抽样的方法来生成表征有源配电系统中功率不确定性的原始场景集。

拉丁超立方抽样是一种分层抽样技术[20]，其核心在于对随机变量的概率分布函数进行分层处理。

设不确定集D中的变量个数为M，且对其中的任意一个变量dm，其概率分布函数为

Ydm=F(dm)

(27)

设生成的初始场景个数为N，则拉丁超立方抽样的具体步骤如下：

(1)将概率分布函数的y轴进行N等分，并对每个区间的中点进行抽样，记为ydm(n)=(n-0.5)/N，针对每个概率ydm(n)即可求得其对应的变量样本值dm(n):

dm(n)=F-1(ydm(n))

(28)

通过以上步骤，可以依次得到变量dm在N个场景中的值，再依次对不确定集D中的M个变量进行上述处理，则可以得到M×N阶的样本矩阵X。但在矩阵X中，对于其中的任意变量dm，其对应的N个值都是依次排列的，这使得各变量之间相关性很强，不符合场景生成的实际要求，因此需对矩阵重新排序以调整场景之间相关性。本文采用Cholesky分解法[21]对各场景中的值进行排序：

(2) 随机生成M×N阶矩阵S，用以表示X中每个变量的样本值排列顺序，S中的每一行都由整数 1～N组成随机数列；

(3)计算S中各行之间相关系数，形成相关系数矩阵ρS，对ρS进行Cholesky分解得到矩阵Q，并求得各行之间不相关的矩阵S1：

ρS=QQT

(29)

S1=Q-1S

(30)

(4)可用S1矩阵中各行的元素排列顺序来代替S中的行向量，即使得X中每行的元素排列顺序与S1矩阵中的元素排列顺序相同。进行排序后的样本矩阵X中的每个列向量即为一个场景，且各场景之间是相互独立的，关联性较小。

2.2.2场景削减

通过拉丁超立方抽样得到的场景集能够较好地覆盖整个样本空间，但场景数目较多，为了提高计算效率，需将场景集进行有效削减，筛选出能充分逼近原始场景集的典型场景集。本文采用同步回代消除法[22]来对原始场景集进行削减，步骤如下：

(1)设定场景集中每个场景的概率均等，即任一个场景的概率p(ci)为

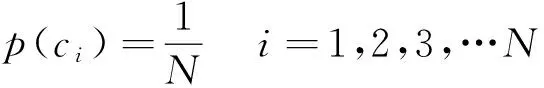
式中ci表示场景集中的第i个场景。

(2)对于每个场景ci，计算其与其他场景之间的Kantorovich距离，找到距离其最近的场景并标记，形成最小场景距离矩阵DC，即：

DC(i)=min{‖ci-cj‖2,j∈[1,2,3,…N],

j≠i},i∈[1,2,3,…N]

(32)

(3)对于每个场景ci，将其最小场景距离与其概率相乘，求得其概率距离，并找出场景集中概率距离最小的场景c*,将其从场景集中剔除，此步骤可以剔除掉场景集中概率很小而且不具有代表性的场景。

min{DC(i)p(i)|i∈[1,2,3,…N]}

(33)

(4)寻找到距离被剔除场景c*最近的场景，并将c*的概率添加到该场景的概率中。

(5)改变场景总数N=N-1，返回步骤(2)重复进行场景削减过程，直至削减后的场景数满足需要保留的典型场景数目要求。

2.2.3基于场景分析法进行有功无功协调优化求解

基于场景生成和削减后得到的典型场景集，可以在充分逼近原场景集合的情况下减少场景数目，避免由于场景数目庞大给模型求解带来的计算负担。针对典型场景集中的单个场景ci，表征功率波动情况的向量d即为已知，则2层鲁棒优化问题可以转化为只包含其主问题的优化模型：

式中di表示场景ci中的光伏、风电以及负荷的有功功率和无功功率。

对典型场景集中的场景进行有源配电系统有功无功协调优化调控，从中选取电压偏差最大的场景，即可近似为本模型中的最恶劣场景，在该场景下也能满足系统运行安全性要求的优化解，即为求解得到的鲁棒优化解。基于场景分析的有源配电系统有功无功协调鲁棒优化策略的整体步骤如图2所示。

3 算例分析

本文在修改后的IEEE 14节点配电测试系统上验证所提方法的有效性，测试系统的结构拓扑图如图3所示，系统基准容量为100 MV·A，基准电压为 23 kV，系统的线路参数和负荷数据参见文献[23]，设全网各节点的电压安全范围为[0.95,1.05] pu。

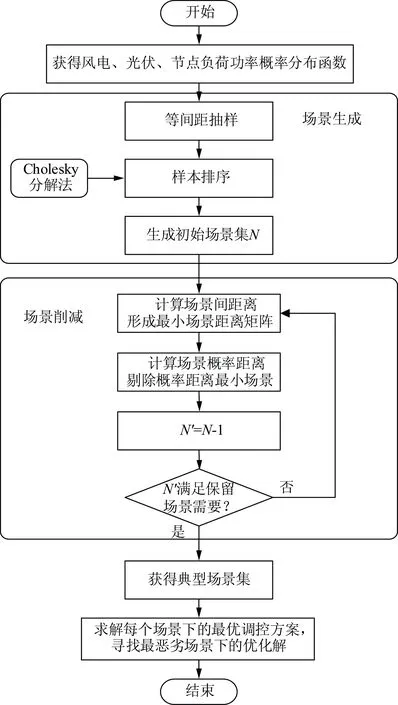
图2 基于场景分析的有源配电系统有功无功协调鲁棒优化策略求解步骤Fig.2 Robust optimization strategy of active distribution on the basis of scenario analysis

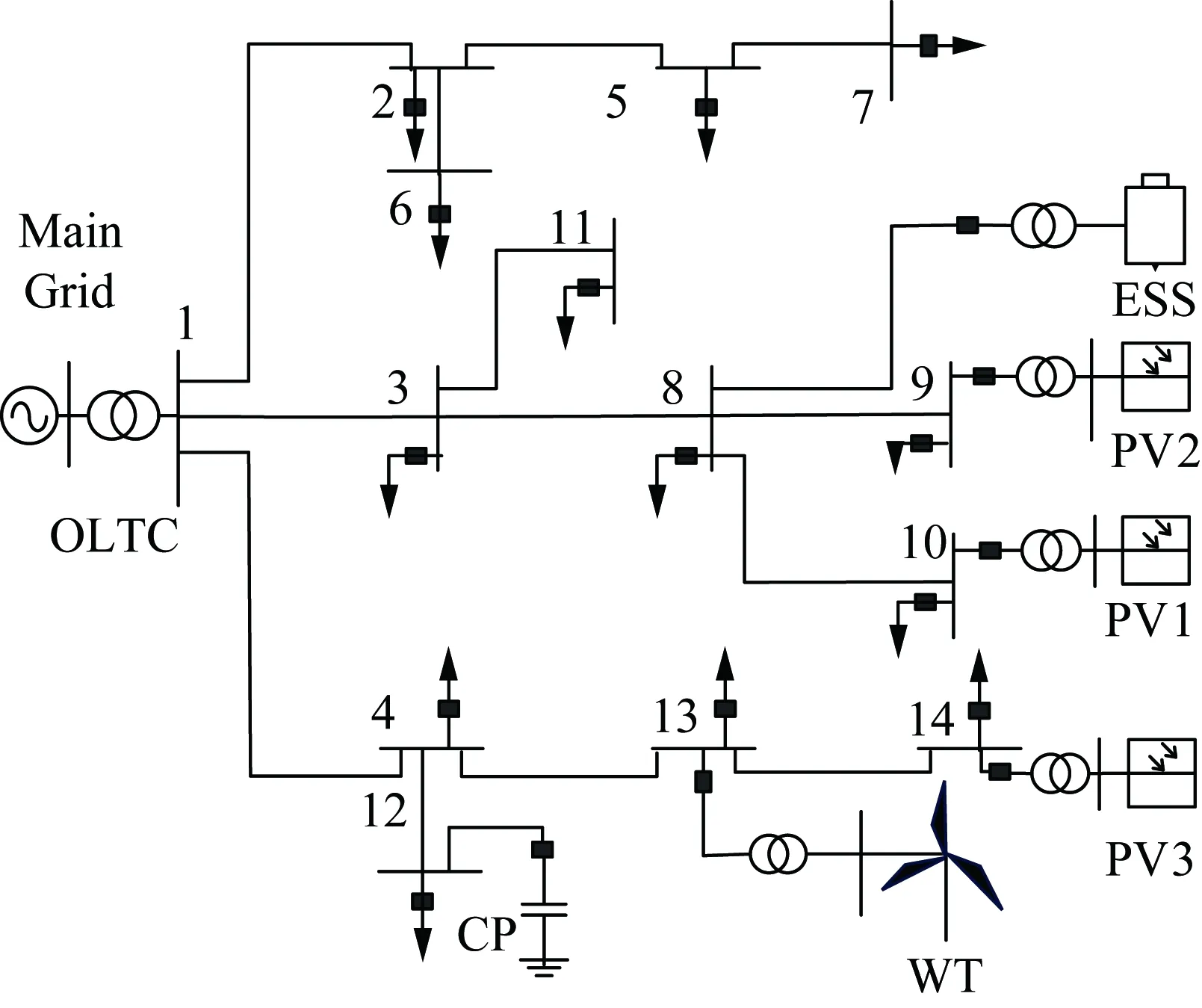
图3 修改后的IEEE 14节点配电系统Fig.3 The modified IEEE 14 distribution system

在原有IEEE 14节点配电系统网络结构基础上，添加了光伏、风电、储能以及OLTC、电容器等，具体为：

(1)系统与上层电网的连接点处接有OLTC，其可调电压范围为0.95 pu到1.05 pu，调节步长为0.005 pu，全天最大动作次数为10次；

(2)节点9、10和14处分别接有分布式光伏PV1，PV2和PV3，其装机容量为30 MW；

(3)节点13处接有双馈风电机组WT，其装机容量为5.6 MW；

(4)节点8处接有储能装置ESS，其容量为 300 MW，充放电功率上下限均为5 MW；

(5)节点12处接有补偿电容器，其调节容量为12 MV·A，调节步长为3 MV·A，全天最大动作次数为10次。

系统总负荷和可再生能源出力的全天预测功率曲线如图4所示。算例中采用相对误差来表征系统中负荷功率变化和可再生能源出力波动的不确定性，本算例考虑其服从正态分布[24]，设定为服从分布N(0,0.12)。目标函数中惩罚因子α设为1 000。

算例仿真是在MATLAB R2014a编译环境下，采用Yalmip优化工具建模[25]，调用Cplex(版本12.5)求解。编译算法的电脑配置为Intel(R) Core(TM) i7-5500 2.40 GHz，8 GB内存。

图4 系统总负荷和可再生能源出力的全天预测曲线Fig.4 Forecast curves of load and renewable energy

3.1 结果分析

对算例采用基于有功无功协调的有源配电系统鲁棒优化策略求解，得到最恶劣场景下有源配电系统的有功无功协调调控计划，即模型的鲁棒解如图5所示。

从图4中可以看到，在09:00—14:00时段，由于可再生能源出力超过了负荷需求，产生功率倒送，易引起节点电压越限等问题，因此需要综合协调有源配电系统内的有功无功资源，防止系统内出现电压越限等安全性问题。图5展示了鲁棒解中储能的有功无功出力，可再生能源的无功出力及有功削减量。

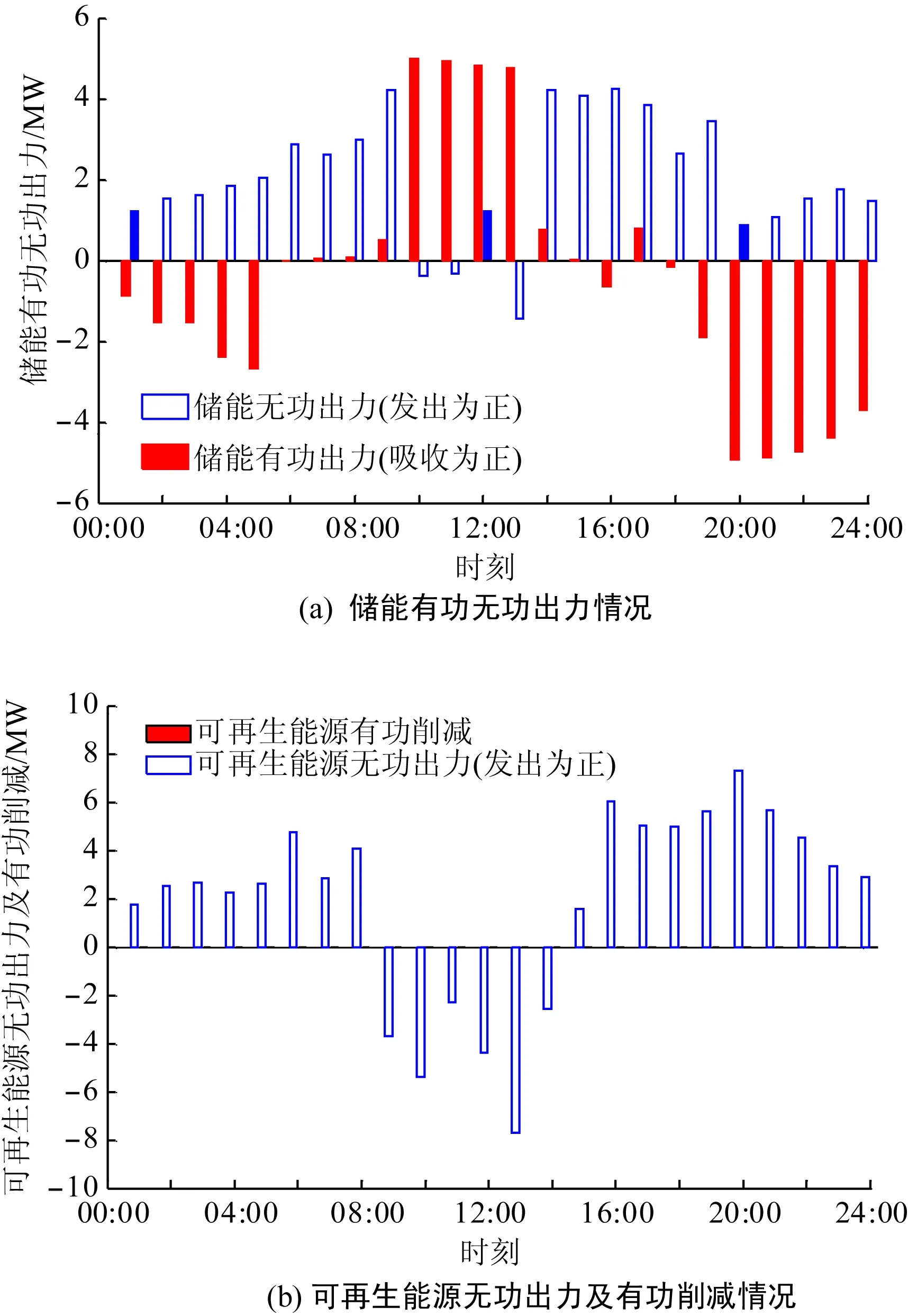
图5 储能及可再生能源有功无功出力情况Fig.5 The optimization results of energy storage and renewable energy

从仿真结果看出，储能在09:00—14:00时段吸收有功功率，以缓解系统中的潮流倒送情况，降低节点电压幅值，而可再生能源则在倒送时段吸收无功功率以使越限节点电压幅值降至安全阈内，可再生能源有功功率基本无削减，保证了可再生能源的利用率。

为进一步体现有功无功协调优化的优势，针对鲁棒调控计划对应的最恶劣场景，将有功无功协调优化结果与不考虑可再生能源以及储能的有功无功功率极限情况下的优化(仅以OLTC档位，补偿电容器投切档位，可再生能源以及储能的有功出力为控制变量)结果进行比较，图6为2种优化情况下系统的网损和可再生能源功率削减情况对比，图7为优化前，有功无功协调优化以及不考虑功率极限优化情况下各时段的最大电压幅值偏差对比。

观察图6可以看到，在不考虑可再生能源和储能的有功无功功率极限情况下，由于可再生能源功率倒送引起电压越限情况较为严重，仅依靠传统无功控制手段无法保证系统安全稳定运行，因此在功率倒送时段削减部分可再生能源出力，以使越限节点电压幅值降至安全阈内；而在有功无功协调优化情况下，由于储能、风电和光伏在功率倒送时段及时调整其无功出力，避免了可再生能源功率削减的情况，可再生能源功率削减量为0，保证了可再生能源的利用率。观察3种情况下的电压情况，可以看到2种优化方法均将越限电压降至安全范围内，且在大部分情况下，有功无功协调优化后电压幅值偏差最小，可见通过有功功率和无功功率的协调优化，可以为系统电压提供更多的调节裕度。综上所述，在系统出现安全性问题时，通过有源配电系统有功无功协调优化方法能够充分发挥有功功率和无功功率在调节系统节点电压的作用，在保证系统安全稳定运行和可再生能源利用率方面都更有效。

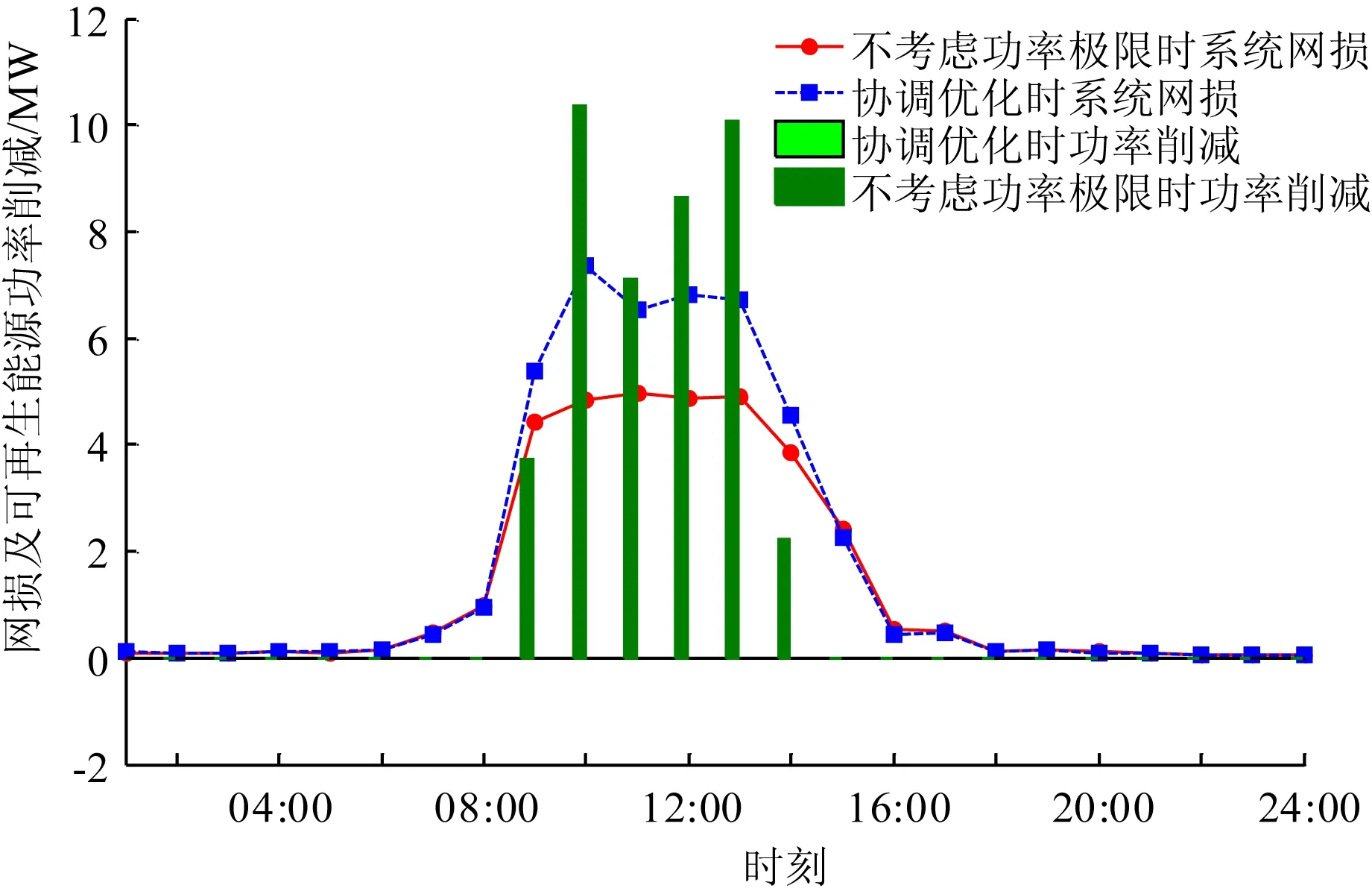
图6 协调优化和不考虑功率极限优化系统网损和可再生能源削减对比Fig.6 Comparison of network losses and renewable energy reductions

图7 最大电压幅值偏差对比Fig.7 Comparison of maximum voltage amplitude deviations

3.2 算法分析

进一步分析有源配电系统有功无功协调鲁棒优化策略在应对可再生能源出力和负荷波动不确定性方面的有效性。本文将鲁棒优化求得的策略解与确定性有功无功协调优化策略进行比较，其中确定性优化策略为在忽略可再生能源出力和负荷功率的不确定性，仅以其日前预测数据代入优化模型中所求得的策略解。根据风电、光伏以及负荷功率波动预测误差的概率分布函数，采用蒙特卡洛模拟方法对上述算例随机抽取100个场景样本，分别在鲁棒优化策略和确定性优化策略下对这100个场景进行潮流计算，得到2种优化策略下每个场景中各时刻最大电压幅值偏差如图8所示。

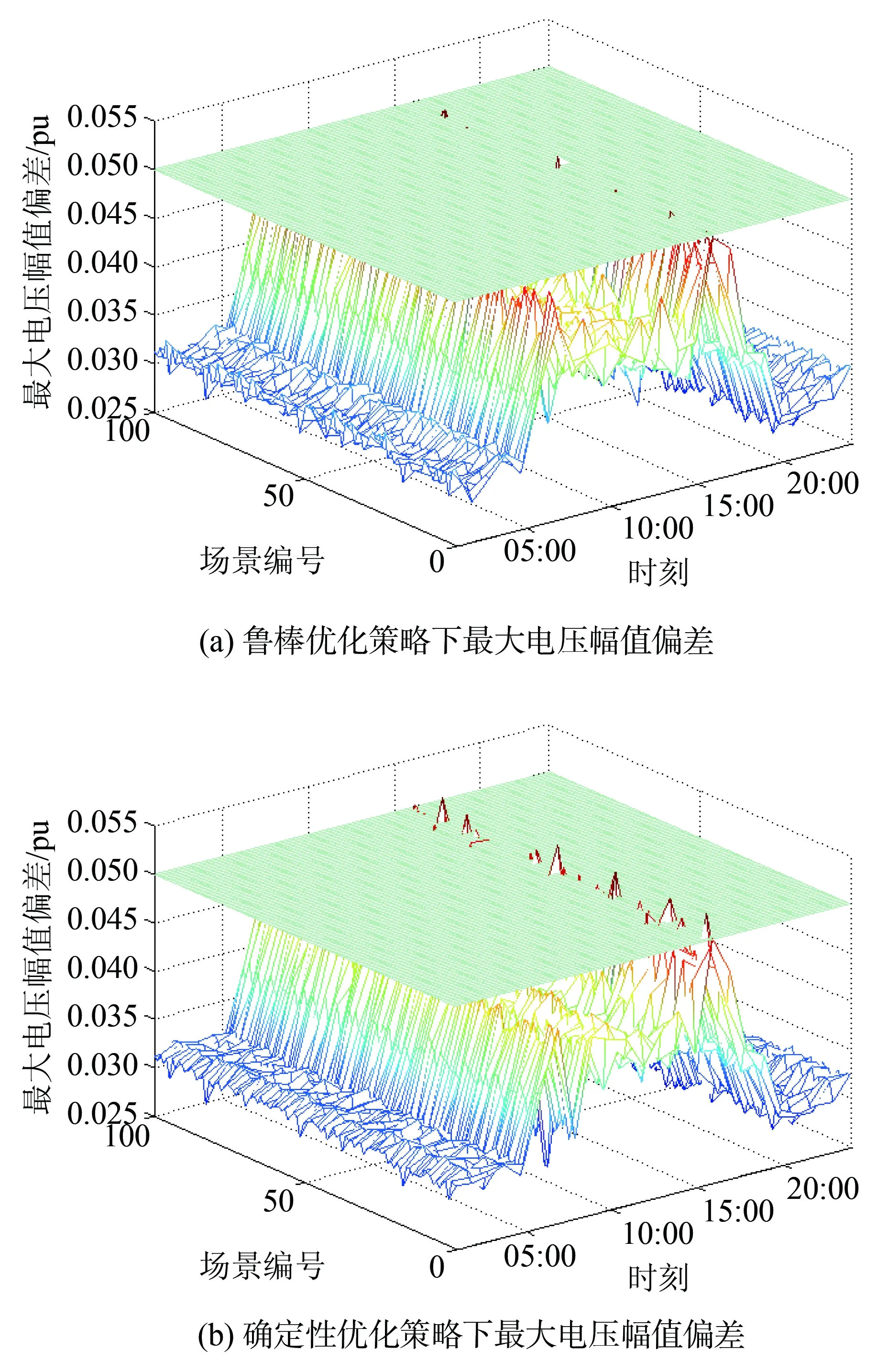
图8 2种优化策略下系统最大电压幅值偏差对比Fig.8 Comparison of maximum voltage amplitude deviations of different optimization strategies

图中平面表示节点电压幅值偏差的上限。从图8可知，确定性有功无功优化策略由于忽略了可再生能源出力和负荷功率预测误差对系统运行的影响，不能保证全天所有时刻系统所有节点电压幅值始终满足电压安全约束。而采用鲁棒优化策略则能有效地减少由于功率波动和预测误差导致节点电压越限的情况，说明本文所提出的有源配电系统有功无功协调鲁棒优化策略能够较好地适应可能出现的功率波动情况，具有一定的鲁棒性。同时，分别对鲁棒优化策略和确定性优化策略情况下电压越限情况出现的比率进行统计，确定性优化策略下电压越限场景比率为30%，鲁棒优化策略下电压越限场景比率为5%。可以看到，与确定性优化策略相比，鲁棒优化策略下电压越限情况出现几率大大降低，证明本文提出的有功无功协调鲁棒优化调控策略能有效应对不确定性对有源配电系统运行的影响，提高系统运行的安全性。

4 结 论

本文针对分布式可再生能源出力不确定性和功率预测误差对有源配电系统调控运行的影响，提出了一种基于场景分析的有源配电系统有功无功协调鲁棒优化策略，通过场景生成和削减得到能表征功率波动不确定性的典型场景集，从中寻找最恶劣场景及其对应的有功无功协调调控策略，即鲁棒优化策略，使得系统内功率在不确定集内波动时，该优化策略能有效提高系统运行安全性。通过修改后的IEEE 14节点配电系统验证了有功无功协调优化在调节系统电压，保证系统安稳运行方面的有效性和优越性，以及鲁棒优化策略在应对功率波动不确定性方面的有效性。