基于贡献度分层的主动配电网供电能力评估

任佳峰，穆启天，杨用春，高亚静

(新能源电力系统国家重点实验室(华北电力大学)，河北省保定市 071003)

0 引 言

随着电力体制改革的不断深化，作为电网安全校核约束的供电能力，已经成为电力市场交易过程中需要参考的必要信息。而随着分布式电源(distributed energy resource，DER)在配电网系统中渗透率的不断提高，主动配电系统(active distribution system，ADS)供电能力(power supply capability，PSC)的评估难度不断增加。配电网的供电能力是指配电网在满足支路功率约束和节点电压约束条件下所能供给的最大负荷[1]。

对于配电网供电能力的计算，学者们已经有了很多研究。文献[2]基于实时载流量，对电网进行实时静态安全分析，并通过线性规划法计算实时供电能力，并量化评估系统的安全状态，用于评估输电网的安全等级。文献[3]提出一种基于主变互联关系和N-1准则的供电能力计算方法，为城市电网的优化规划提供有效参考依据。文献[4]提出基于潮流计算的最大供电能力(total supply capability,TSC)模型，精确计及了电压降落和网络损耗，针对此模型，采用了基于前推回推的迭代和广义梯度法的求解方法。文献[5]建立了配电网的分层供电能力指标体系和评估方法。文献[6]定义并提出了一系列配电网最大供电能力评估指标。

在中长期供电能力评估中，蒙特卡洛算法得到了普遍的应用。文献[7]运用蒙特卡罗法进行系统状态选择，包括线路故障、负荷水平和风电场风速等多种不确定因素。然后通过分析每次抽样样本，计算得到系统输电能力。文献[8]针对直流线路的供电能力进行了分析和计算，为今后计算交直流混合的供电能力提供了参考。文献[9]分析认为蒙特卡洛法是风电可信容量计算中采用广泛的方法。蒙特卡洛算法的优势在于算法和计算简单、物理意义明确、可以考虑到众多因素。但是其缺点也很明显，蒙特卡罗方法存在计算精度与计算时间的矛盾[10]，即如果想要获得较高的抽样精度，需要大量的抽样点，如果针对每一种情况都进行一次供电能力计算，这将会是非常大的计算量。同时，在网络故障方面，采用N-1故障的比较多，但是在中长期供电能力评估中，考虑N-1不够精确，且故障抽样次数不宜太多。

为了提高配电网中长期供电能力评估的速度和效率，本文针对计算中各部分的不确定性，进行以下几方面的处理。首先针对“源”的不确定性，由于不同的“源”出力水平对配电网供电能力的影响是不同的，因此本文将分布式电源的出力大小进行排序，然后按照贡献度进行划分，最后针对每部分采用相应的处理方法，来协调抽样次数和抽样精度的矛盾；其次，针对网络故障的不确定性，基于线路元件的重要度，对故障元线路进行分层抽样，得到故障的抽样结果；再次，针对负荷的不确定性，采用年负荷的多层模型确定负荷的抽样点。在完成对“源”、网和负荷的抽样之后，利用改进的重复潮流算法，计算求得各种抽样组合情况下的供电能力并计算出相应的供电能力评估指标，从而为中长期电力市场的交易提供必要的指导和支持。

1 影响中长期供电能力的各因素建模

1.1 基于贡献度和均值聚类技术的风、光出力建模

在配电网络中，由于风电和光伏的出力具有不确定性，而且随着分布式电源接入比例的提高，风电和光伏出力会对配电网的供电能力产生很大影响[11]。而且，安装在配电网络中的分布式电源出力越高，配电网的供电能力越大，即出力越大，对配电网供电能力的贡献越大。因此本文将“源(风力发电和光伏发电)”出力的历史数据按照递减顺序排列，可以得到“源”出力的持续时间曲线。以风电出力为例，可以得到如图1所示的风电出力持续曲线。从图1中可以看出，风电的出力集中在中部，较高的出力点和较低的出力点都相对较少。由于“源”出力的高低对于配电网供电能力的影响不同，故根据对供电能力的贡献程度不同，将“源”出力持续时间曲线分成高、中、低3个贡献分区，对不同的分区，采用了不同的处理方法，保证计算速度的同时提高了计算的精度。假设高、中、低3个贡献区的出力点分别为Nh、Nm、Nl，则每个贡献区的出力点所占的比例系数为

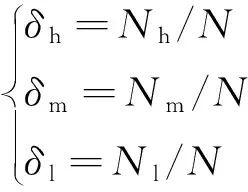
式中：δh、δm、δl分别为高贡献区、中贡献区、低贡献区的比例系数；N为全年的小时数，为8 760 h，N=Nh+Nm+Nl。

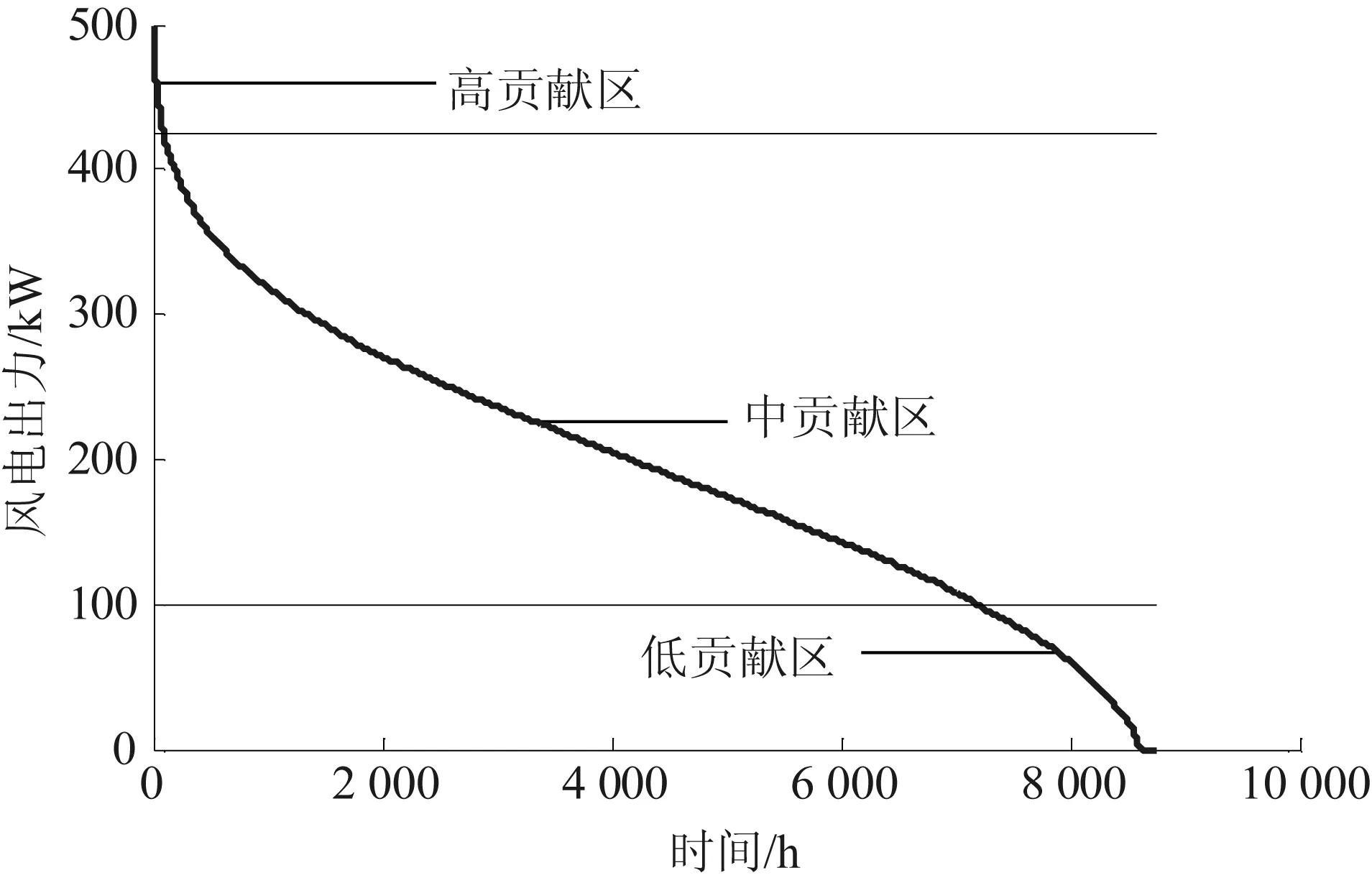
图1 风电出力曲线Fig.1 Output curve of wind power

1.1.1高贡献区抽样

高贡献区的出力点虽然相对较少，但是对于配电网络的供电能力影响较大，不应忽略，因此为了更好地反映高出力点对于供电能力的影响，本文采用拉丁超立方抽样技术选取高贡献区的出力点，以保证抽样点在高贡献区尽可能均匀分布。假设所选抽样点个数为nh，则每种抽样情况对于最终供电能力指标作用的比例系数为

(2)

式中δih为高贡献区的每个抽样点的贡献度。

1.1.2中贡献区抽样

由图1可知，中等贡献区出力点的占比很大，且中间最为集中，逐渐向高贡献区和低贡献区分散，也是分析“源”对配电网供电能力影响最重要的部分。考虑到这些特点，本文采用均值聚类技术对中等贡献区进行划分，抽样点即为聚类的中心，各抽样点比例系数的大小与划分区内出力点的个数有关。假设共划分为nm个区间，每个区间的出力点个数为nmi，i=1，2，…，nm。则每个抽样点的贡献度为

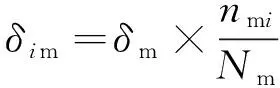
式中δim为中贡献区的每个抽样点的贡献度。

为了确定最佳的聚类次数，本文采用文献[12]的方法确定最佳聚类数。即通过定义改进效率，提出根据改进效率对计算精度和时间成本进行综合权衡，即将改进效率作为聚类数的收敛条件，从而确定各分区中合适的聚类数[12]。改进效率定义为

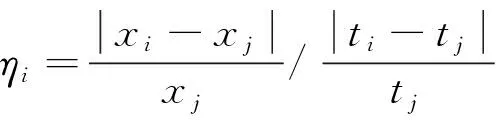
式中：xi、xj分别为聚类数增加前、后的电力系统供电能力；ti、tj分别为聚类数增加前、后的指标计算时间。其中，由于系统处于正常运行状态占据大多数时间，所以计算xi、xj时，选取系统处于正常状态，且负荷为额定值，以简化计算，提高运行速度。

1.1.3低贡献区抽样

低贡献区的出力点相对供电能力的影响是最小的，可以进行简化计算，不会对中长期的供电能力指标的求取产生明显的影响。故设定低贡献区的抽样点只有1个，且出力取0，其最终抽样点的比例系数就是δl。

1.2 基于线路重要度的网络建模

1.2.1元件重要度

研究供电能力时需要考虑系统网络故障的不确定性，可以考虑“N-K”安全校验，但是如果采用蒙特卡洛进行“N-K”安全校验，需要进行大量抽样，否则抽样的效果不好，但是大量的抽样显然不适用于快速的供电能力计算。因此本文考虑到在配电系统中，系统大都处于开环运行状态，所以当离电源较近的上级线路发生故障时，与之相连的下级线路也将停电。也就是说，在配电系统中，各条线路的故障带来的后果有着很明显的区别。因此系统中的线路对于供电能力的影响差异较大。同时，为了保证计算速度，网络总的抽样次数不可以太多。考虑到上述问题，本文从元件重要度的角度考虑，将线路进行划分，然后从不同重要分层的线路中进行抽样。

在同一系统中，各个元件对系统供电能力的影响是不同的，即系统中各元件的重要度不同，因此可以利用元件重要度分析，将对系统供电能力影响较大的元件识别出来。采用Si对事故后果进行量化表示，认为事故后果越严重，其在系统中越重要，本文对事故后果的严重程度利用在“源”和负荷处于额定状态时，故障前后供电能力的变化大小来量化处理。

定义主动配电系统中，某线路发生故障的后果期望函数为

Si=|F(xi)|×p(xi)

(5)

式中：Si为线路i的元件重要度；F(xi)为性能指标，即与xi对应的事故发生后，该事故对系统所产生影响的严重度函数；p(xi)为系统发生某一故障的可能性函数。

F(xi)的具体求解如式(6)所示。

式中：SPSC(xi)为线路i故障后的系统供电能力；SPSC(x0)为线路无故障时的系统供电能力；M为系统线路的个数。

F(xi)的值若大于0，说明故障后，系统的供电能力变小；F(xi)的值若为负，则说明故障线路为系统供电能力的重要约束支路，故障后系统供电能力的提升大于停电部分线路失去的负荷，导致故障后系统的供电能力反而更大。

1.2.2各阶故障抽样

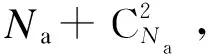
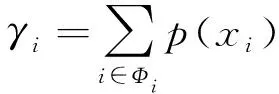
式中：γi为对应故障类型的比例系数；Φi为第i种故障类型的集合。

采用这种方式，即充分考虑到二阶故障这种小概率事件，避免了蒙特卡洛抽样时，抽样结果中对无故障状态进行了大量抽样，同时各抽样情况具有足够代表性，在保证计算精度的同时，减少了抽样次数。

1.3 基于均值聚类技术的年负荷多层模型

由于配电网中负荷点众多，且年负荷曲线也各有不同，如果对每个负荷点都进行抽样，然后再结合“源”的抽样和“网”的抽样结果进行交叉组合后，最后计算每种情况下的供电能力，这无疑将会是非常庞大的计算量。而且对于求取中长期配电网的供电能力来说，也是没有必要的。因此本文先利用多层模型[12]抽样对某一区域总的年负荷持续曲线进行抽样，然后各个负荷的负荷大小按照其额定值占总负荷的多少进行分配。具体计算公式为

(8)

式中：Sload,i为当前i点的负荷水平；Sload,k为某一总负荷抽样值；SiB为某一负荷点的额定负荷；SB为该区域总的额定负荷；l为负荷点的总个数；Nload为负荷的抽样点个数。

年负荷的多层模型如图2所示。其基本思想是先建立1个多层模型，然后将出力点划分到对应的层次内。假设划分为Nload层，每层的个数为Nli，则每层的抽样点对供电能力的贡献为

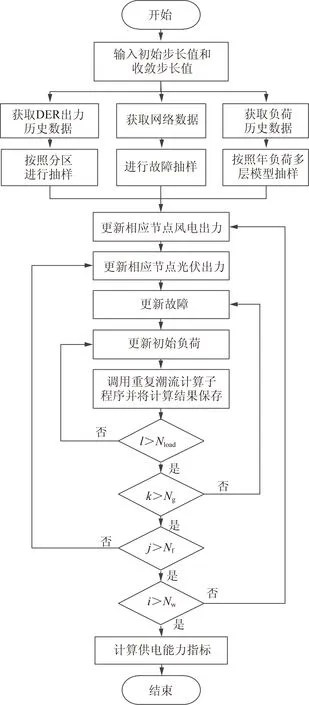
图2 模型求解流程Fig.2 Flow chart of model solution

βi=Nli/N

(9)

基于均值聚类技术的年负荷的多层模型抽样的具体步骤如下详述。

步骤1选择每层负荷的平均初始值Mi(i=1，2，…，Nload)。

步骤2计算N个负荷点Lk(k=1，2，…，N)到各负荷层的距离Dk=|Mi-Lk|。

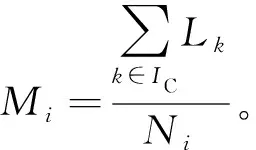
步骤4重复步骤2和步骤3，直到各负荷层的平均值在相邻两次迭代中保持不变。

最后得到的Mi和Ni即为第i层负荷的负荷值和负荷点数目。

2 中长期供电能力评估

2.1 评估指标

(1)年平均供电能力期望值EPSC：

(10)

式中：Nw、δwi分别为风电出力的抽样点数和对应的比例系数；Nf、δfj分别为光伏出力的抽样点数和对应的比例系数Ng、γk分别为故障线路的抽样点数和对应的比例系数；βl为负荷抽样点对应的比例系数；SPSC(i,j,k,l)为风、光、网络故障和负荷确定时对应的供电能力。

(2)年平均可用供电能力MPSC：

(11)

式中SL(k,l)为某一网络故障和负荷确定时对应的供电能力。

(5)供电能力方差VPSC：

(14)

(6)DER对供电能力期望EPSC的贡献量ECADTE，表征DER接入后，供电能力期望EPSC的增量，表示如下：

ECADTE=EPSC-EPSC,N

(15)

式中EPSC,N为没有分布式电源情况下的供电能力。

(7)供电能力的不足概率pDPPSC，表征供电能力小于某一允许值的概率。

pDPPSC=∑pdp(i,j,k,l)

(16)

式中pdp(i,j,k,l)为对应情况下，小于允许值A的供电能力所对应场景的发生概率。

(8)供电能力的不足量SDAPSC，表征供电能力期望小于某一允许值的量。

SDAPSC=∑[A-SPSC(i,j,k,l)]×pdp(i,j,k,l)

(17)

式中A为供电能力允许值，当SDAPSC<0时，A值为0。

2.2 单场景下供电能力的计算模型

(1)目标函数：

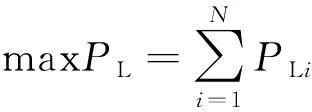
式中：PL为配电网能够供应的最大有功负荷；N为负荷点数；PLi为负荷点i处的有功负荷。

(2)约束条件：

(19)

(20)

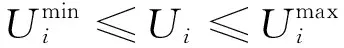
(22)

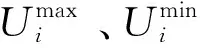
2.3 模型求解

按照定义，配电网的供电能力[13]等于模型中恰有一约束起作用时配电网所供应的总负荷，最直接的求取方法是重复潮流法。其基本思想为：从当前运行点出发，按照一定的负荷增长模式不断增大系统负荷并反复进行潮流计算，以此确定系统供电能力[14]。本文采用文献[15]中的变步长重复潮流计算进行求解，详细过程见文献[15]。

3 算例分析

3.1 系统概况

本文选用改进的IEEE 14节点系统进行供电能力评估，利用MATLAB进行仿真计算。考虑到配电网在正常情况下一般开环运行，本文移除了14、15、16这3条支路，使系统成为14节点13条支路的单电源辐射型网络，其结构如图3所示。

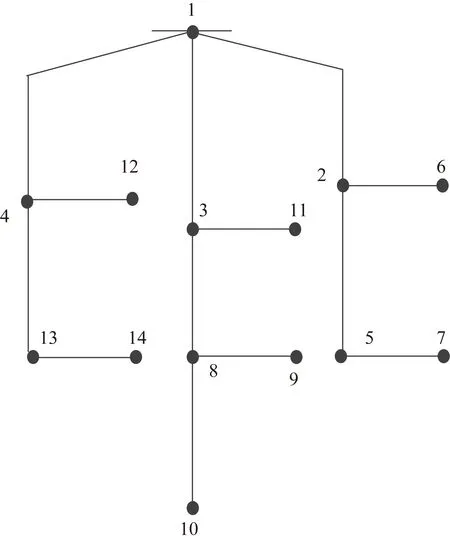
图3 改进IEEE 14节点图Fig.3 Improved IEEE 14-node diagram

图3中节点1为平衡节点，其余为负荷节点，系统基准容量为100 MV·A，基准电压为23 kV。线路功率上限取其热稳极限容量，电压允许变化范围取(1±5%)pu。

除固定负荷外，考虑接入的ADS“元”包括风电(WG)、光伏(PV)，接入情况如表1所示。

表1ADS“元”的接入情况
Table1Connectionsofthe“Units”ofADS

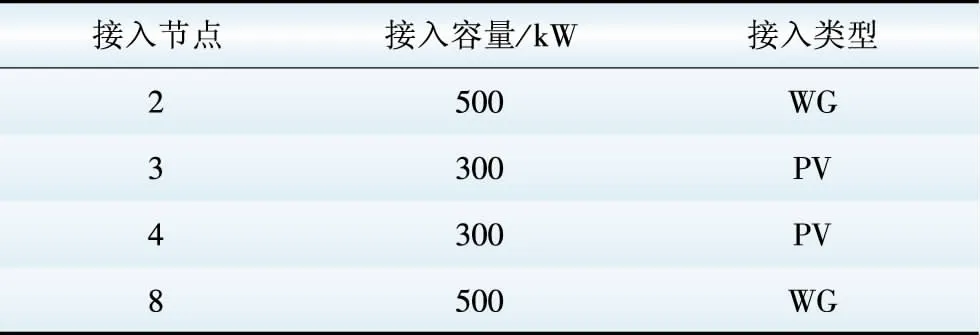
3.2 供电能力计算

取某风电场和光伏电厂2013年全年的历史数据作为本文风电场和光伏电站的出力，设定高贡献区为出力大于最大出力的0.9倍，低贡献区为小于最大出力的0.2倍，中间部分划分为中贡献区。对于风、光的抽样，其中中等贡献区的最佳聚类次数为4，所以中等抽样的次数为4。取高贡献区抽样点数与中等抽样次数同为4次，低贡献区抽样次数为1次，共9次。本文将元件的重要度设定为3层，则总故障的抽样次数为9(1+2+6)次。各线路的故障率取固定值0.001。为了证明本文方法的有效性和相比传统方法的快速性，用蒙特卡洛抽样的方法进行验证。其中对分布式电源和负荷各抽样100次，对于故障，本文将所有的零阶、一阶和二阶故障全部进行考虑，结合本算例，一共92个，故蒙特卡洛法总的计算次数为9.2×107(100×100×100×92)次。本文方法下，风电场出力抽样的分布如图4所示，光伏电厂出力抽样分布如图5所示，所有线路的重要程度如表2所示。

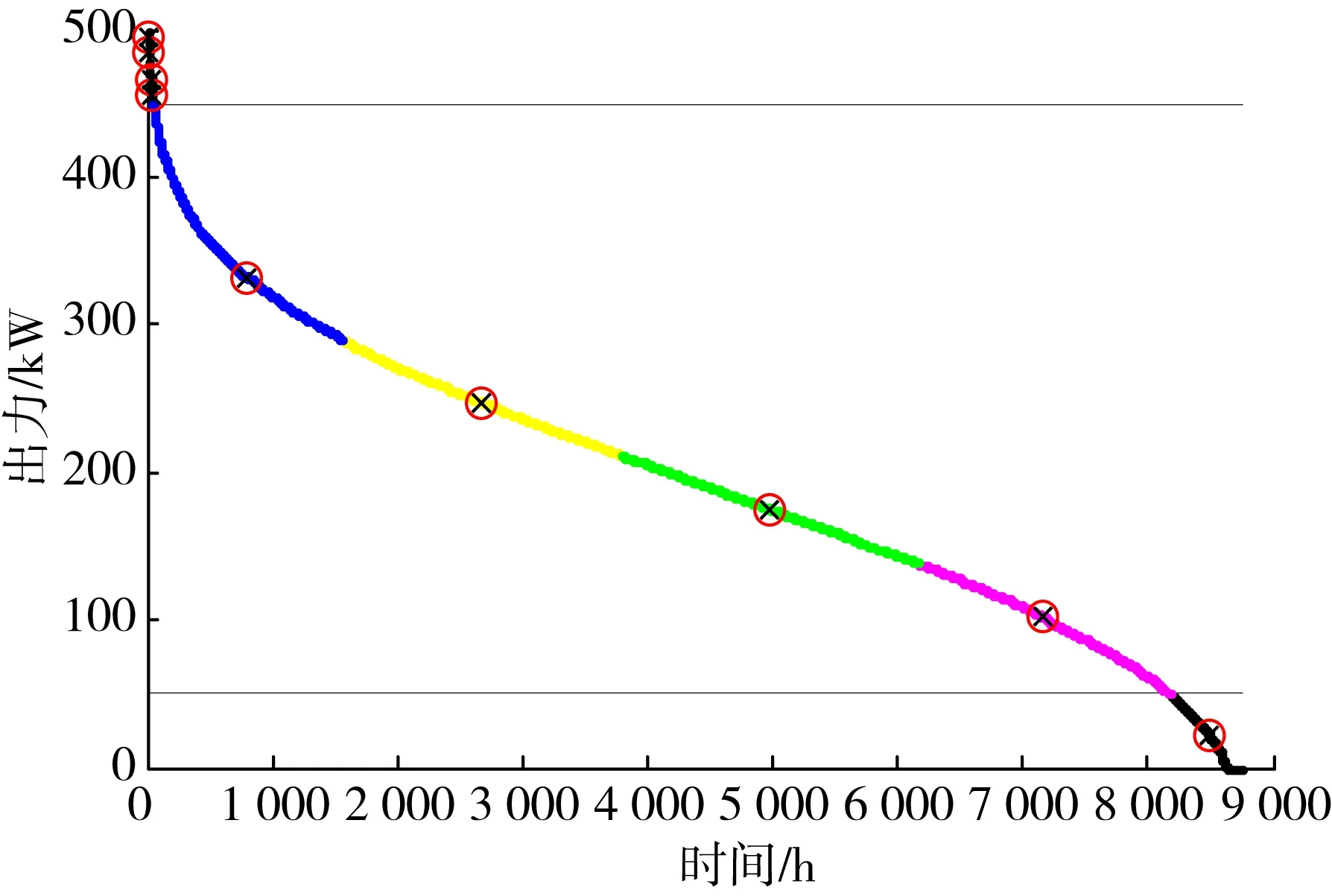
图4 风电出力抽样分布Fig.4 Output sampling map of wind power

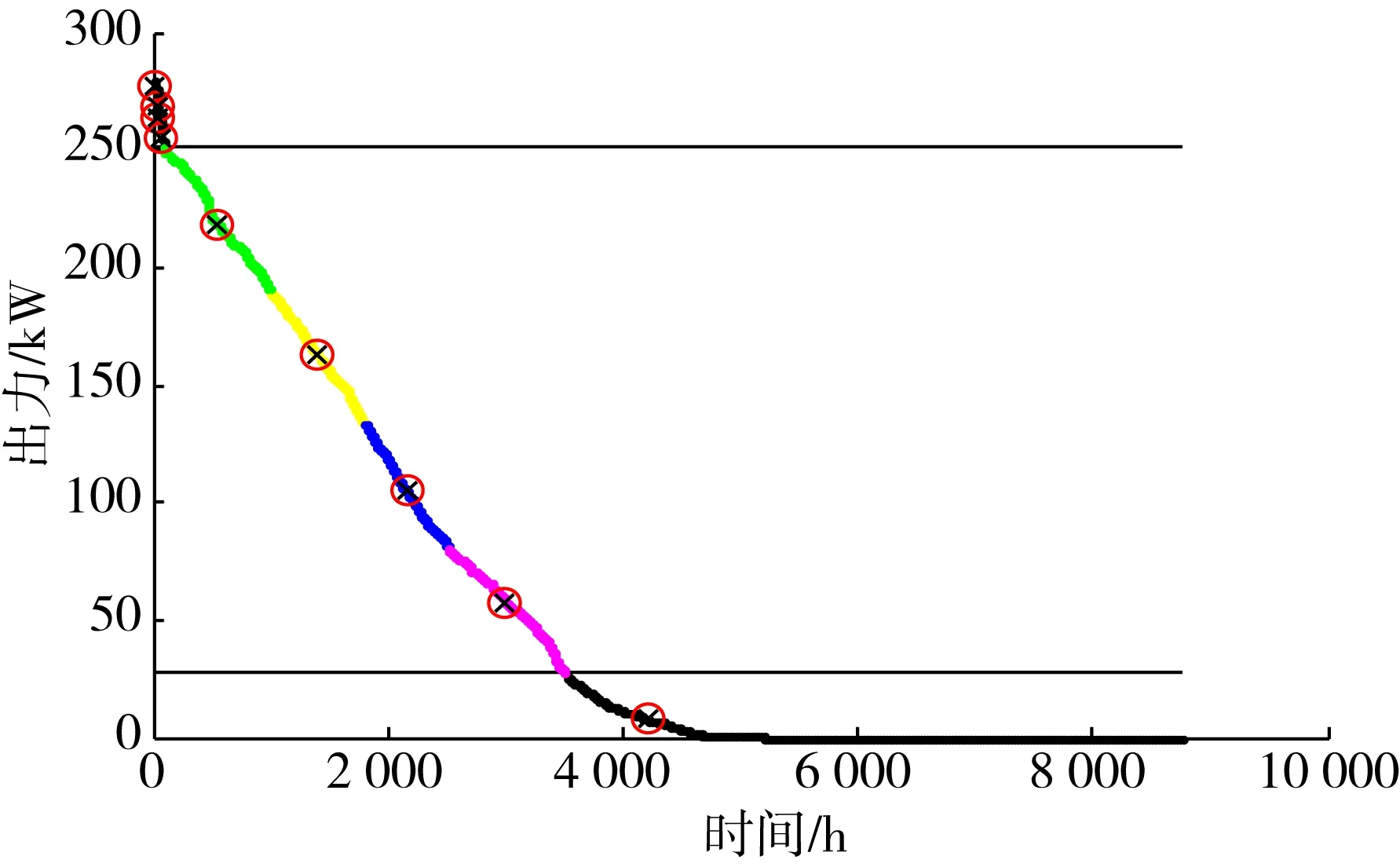
图5 光伏出力抽样分布Fig.5 Photovoltaic output sampling distribution

设定所有线路划分为3层后，通过聚类分析，各层的线路分配为：第一层包含线路1、7、8；第二层包含线路3；第三层包含线路2、4、5、6、9、10、11、12、13。

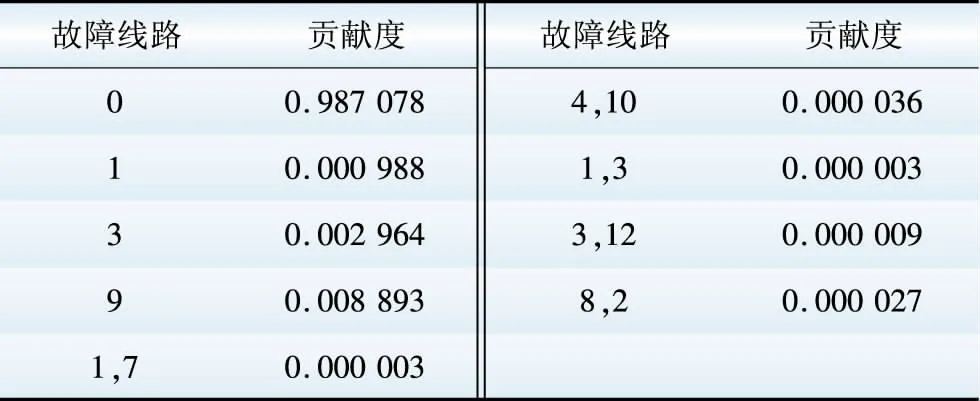
按照本文的故障抽样方法，线路故障的抽样次数为9，各抽样故障的比例系数如表3所示。

表2线路重要度
Table2Lineimportance

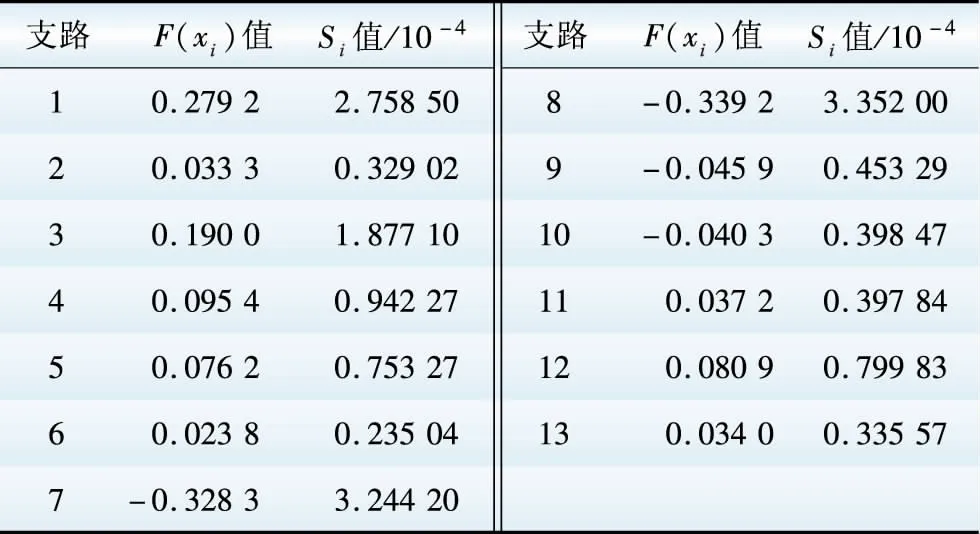
表3 故障比例系数Table 3 Ratio coefficient of faults

负荷的年度和多层模型分布如图6所示。

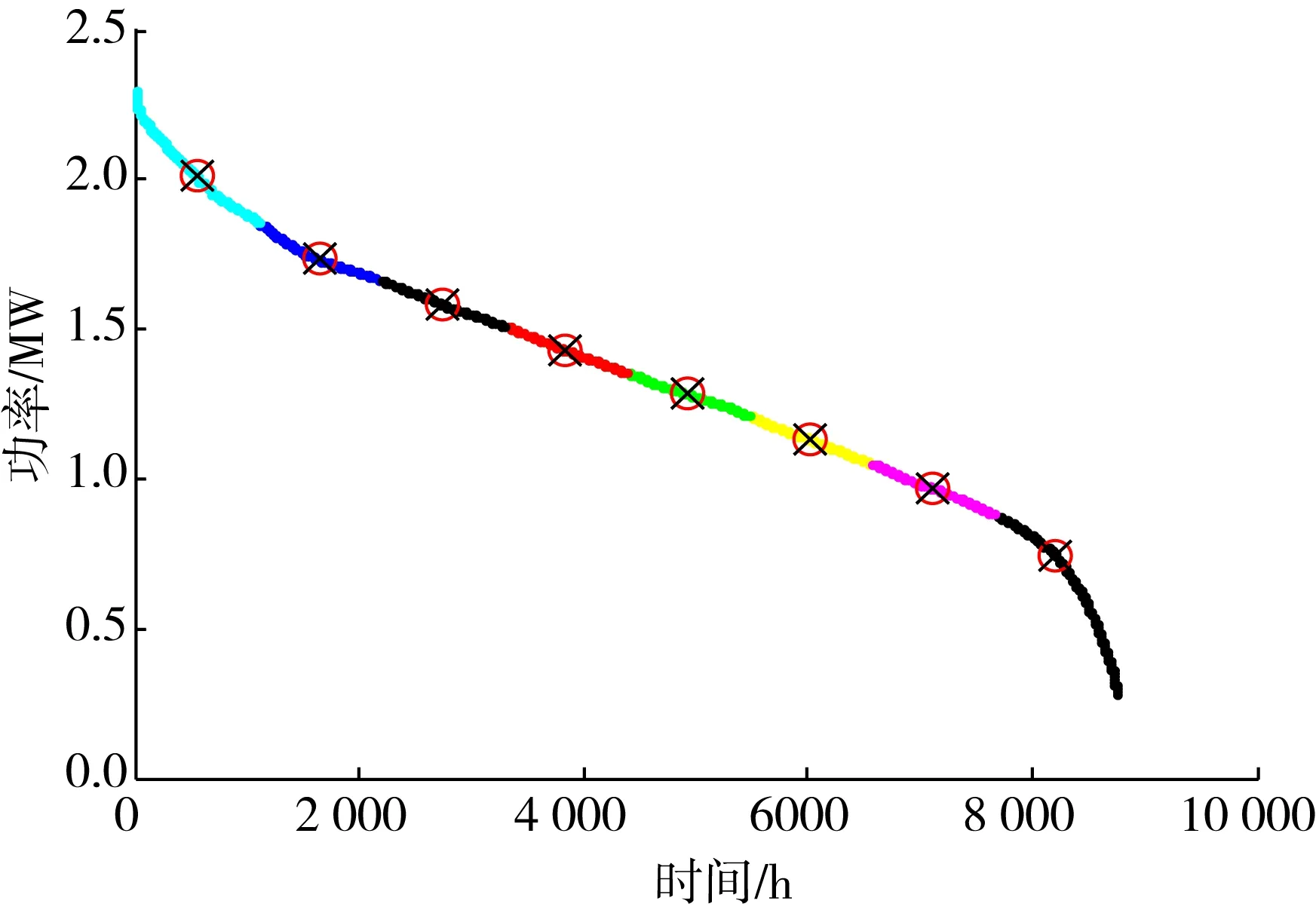
图6 负荷抽样分布Fig.6 Load sampling distribution

图7为风电和光伏抽样对供电能力的影响。其中：图7(a)为系统故障和负荷均不发生变化时，DER出力抽样对系统供电能力的影响；图7(b)为蒙特卡洛抽样方式下，系统故障和负荷均不发生变化时，DER出力抽样对系统供电能力的影响。图8为风电出力和故障抽样对供电能力的影响。其中：图8(a)为光伏出力和负荷均不发生变化时，故障抽样和风电出力抽样对系统供电能力的影响；图8(b)为蒙特卡洛抽样方式下，光伏出力和负荷均不发生变化时，故障抽样和风电出力抽样对系统供电能力的影响。

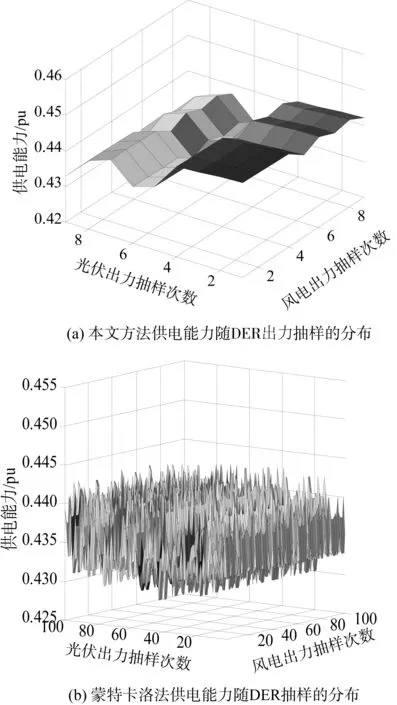
图7 风电出力和光伏抽样对供电能力的影响Fig.7 Influence of wind power and photovoltaic sampling on power supply capacity

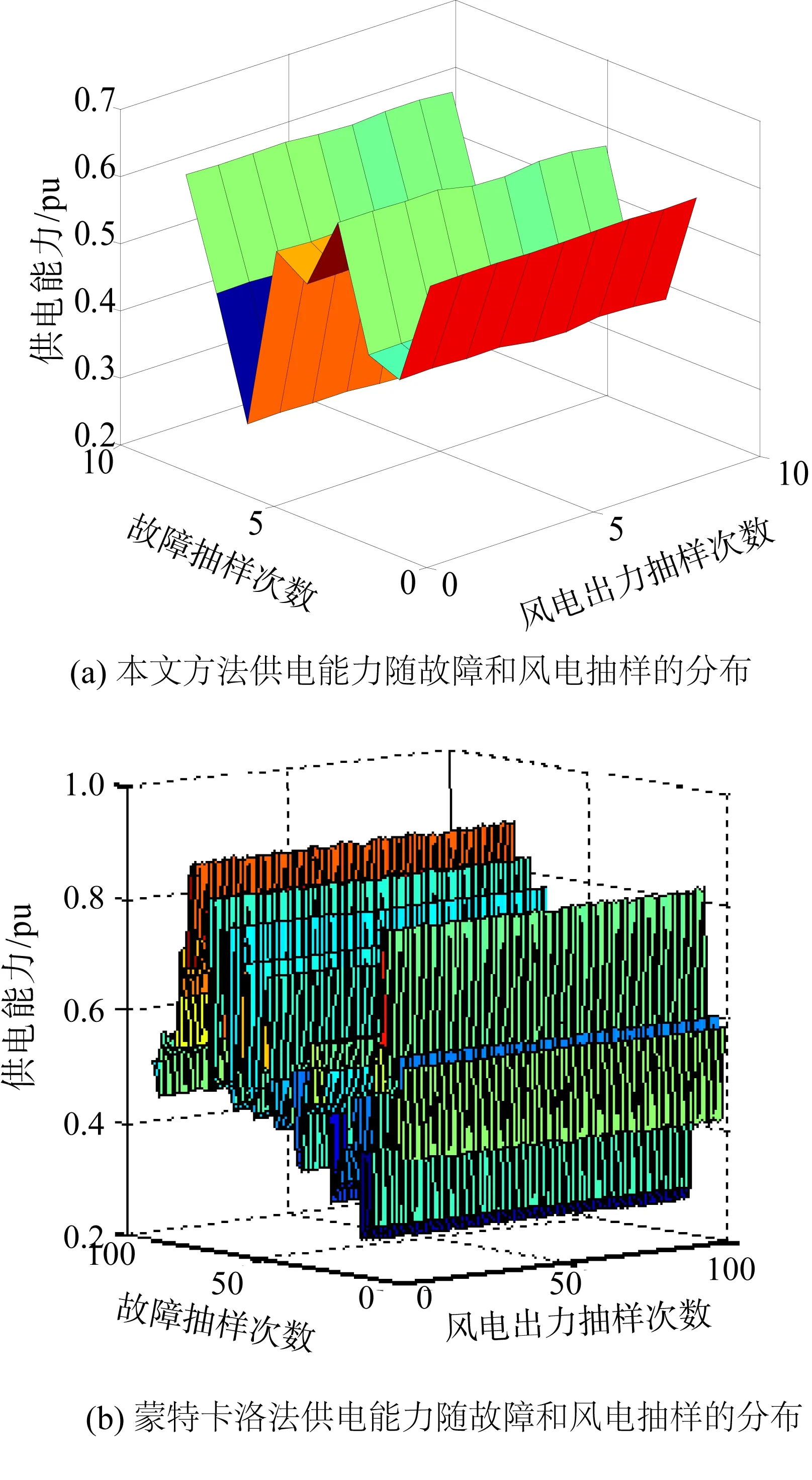
图8 风电出力和故障抽样对供电能力的影响Fig.8 Impact of wind power and fault sampling on power supply capacity

3.3 供电能力评价指标求取

表4对比了按照本文所提方法和单纯蒙特卡洛方法求取供电能力指标和计算时间的结果。

表4供电能力指标结果
Table4Resultofpowersupplycapabilityindexes

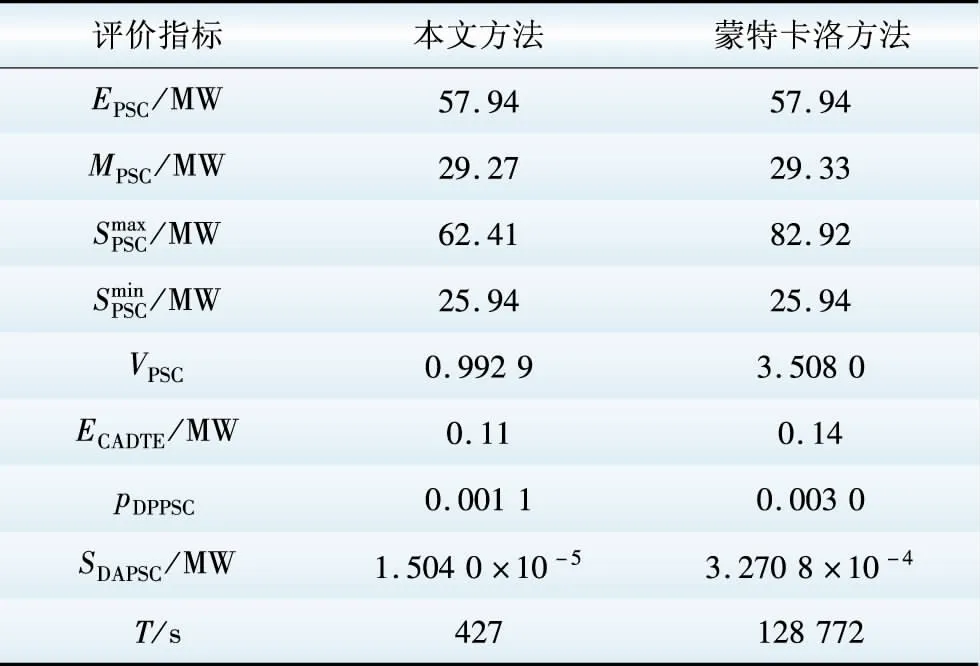
从表4的结果可以看出，利用本文所提方法，在求取供电能力期望和裕度方面，与蒙特卡洛方法的结果很接近，说明利用该方法进行配电网中长期供电能力评估时，在求取关键性指标(年平均供电能力期望值和年平均可用供电能力)时具有可行性。但是在求取最大供电能力值时，这2种方法求取结果又存在明显差别，这是因为蒙特卡洛方法的抽样次数很多，所以可以考虑到极为特殊的运行状态，而本文的方法为了快速求取配电网的年平均供电能力期望值和年平均可用供电能力，对出现概率较小的极端情况考虑不全，因此在最大供电能力方面，二者有明显差距。指标供电能力方差是对这2种方法的一个评价指标，反映出蒙特卡洛法由于其随机性，导致各次结果差距较大，因此整体方差较大。同时，由于蒙特卡洛庞大的抽样次数，导致运行时间比本文方法长出许多，这也是本文所提方法的一大优势。

3.4 收敛性检验

为了检验2种方法的计算结果是否收敛，本文对2种方法计算出的年平均供电能力期望值进行收敛性检验。

(23)

由于指标中已经计算了VPSC，所以式(23)可以简化为

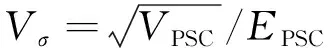
本文方法和蒙特卡洛方法的Vσ分别为0.017和0.032。由此可以看出，本文方法的收敛性相较于蒙特卡洛法要好，而且大大简化了计算时间。

4 结 论

由于传统的中长期供电能力评估时间较长，因此本文提出了一种快速计算和评估中长期配电网供电能力的方法，在提高中长期供电能力评估速度的同时，兼顾到评估的精度。为此，本文通过分别对分布式电源、网络和负荷进行抽样，并定义了一系列供电能力评估指标，从数值大小、波动情况、充裕情况、接入DER的贡献程度等多个角度对供电能力进行评价，为电网调度及运行提供了量化的参考依据。

算例结果表明，本文计算方法所得结果相比于蒙特卡洛法进行抽样计算的结果，能够较好地模拟实际配电网运行状况，而且极大地提高中长期供电能力评估的速度；评估指标的提出能够对中长期供电能力评估提供重要的参照价值；评估结果对指导ADS的优化运行，发掘配电网的供电能力，提高配电网对DER的消纳能力有着重要的指导作用。