水-热-力耦合的单管冻结理论及其数值模拟

刘纪峰, 张会芝,余 照, 付佳宁

(1.三明学院 建筑工程学院， 福建 三明365004;2.工程材料与结构加固福建省高等学校重点实验室(三明学院)， 福建 三明365004)

0 引言

城市地铁旁通道施工常处于复杂的工程地质和水文地质环境，控制不好，很容易造成工程事故[1-3].人工冻结法加固地层具有抗渗性好、强度高、不受深度限制、环境友好等优点，在地下工程施工中得到广泛应用，但其冻胀融沉需加以预控[4].目前，人工冻结法的主要研究方法包括试验研究[5,6]、理论分析[7,8]、工程实测[9,10]和数值模拟[12-14]等.以上研究方法各有其优点和不足.考虑到问题的复杂性，对人工冻结的相关研究要综合选择各方法的优点，避免单一手段的不足.在以往研究的基础上，推导考虑水-热-力耦合的土体冻结理论公式并基于ANASYS二次开发进行其单管冻结的数值模拟，通过对比分析验证该理论的有效性.

1 水-热-力耦合的软土冻结理论

1.1 模型假设

模型假设如下[15-17]：(1)水分迁移只以液态水形式进行，忽略气相和液相之间转变时水分的蒸发转移；(2)土的冻结主要是由热传导控制；(3)忽略荷载作用下土中冰点的降低；(4)土体固结已完成，忽略冻结过程中未冻区的固结；(5)冻结过程中土颗粒体积不变；(6)土体为各相同性体.

1.2 经验公式选取和公式推导

忽略单元体冻结过程中热对流的作用，传导产生的净热流量，等于水冷却(热容量C)时的热量与水转化为冰时的相变潜热之和(潜热L).

热传导温度场方程选用考虑潜热的Harlan[19]方程：

(1)

热量与温度关系用Fourier定律描述, 其含义为单位时间通过单位面积的热流量和温度梯度成正比，即：

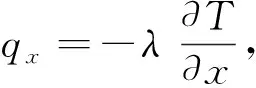
(2)

其中：q为热流密度，J/(m2·s)；λ为导热系数，W/(m·℃)；T为温度，℃；C为体积热容量，J/(m3·℃);t为时间，s；L为潜热，J/kg；ρi为冰的密度，kg/m3；θi为冰体积分数.负号表示温度梯度的方向和热流方向相反.

将式(2)代入(1)并扩展到三维场得到 ：

(3)

在土的冻结过程中，单元体中由于压力梯度的建立和冰的形成使得从孔隙中流出的液态水被保存下来，考虑物质迁移平衡过程，可以得到：

(4)

其中：ρl为未冻水(液态)密度，kg/m3；θl为未冻水体积分数；Qx为流量，m3/s.

方程左边代表通过单元体某方向两个面的净物质流量，右边所指的是未冻水及冰形成产生的物质流量.

引入描述物质扩散过程的Fick定律[15]:

(5)

其中：Pl为未冻水压力，Pa；k为对流传质系数，m2/(s·Pa).

将式(5)代入式(4)并扩展成三维形式，可得稳态和非稳态下的物质迁移方程为：

(6)

压力、密度与温度关系引用Clapeyron方程描述：

(7)

其中：Pi为冰压力，Pa；Pl为液体压力，Pa；Tk为开尔文温度(K=℃+273.16)；T0为参考温度，273.16 K.

假设在0 ℃冰未产生，所有的孔隙都被未冻水占据，未冻水量与温度关系的半经验公式选用线性关系[16]：

(8)

式中n0为冻土的初始孔隙率.

基于Shen[19]关于冰压力分布的建议，假定冰压力在冻结前缘是线性分布的，对于二维有：

(9)

式中k为对流传质系数，m2/(s·Pa).

式(3)和式(6)～(9)有T，θl，θi，Pl，Pi五个未知量，一旦这些量求出，则其中的冰压力Pi及液体压力Pl可被作为应力分析有限元中的初始应力，得出冻胀应力为：

σ0=(Pi+Pl)δ,

(10)

式中δ为克罗克内尔符号.

冻胀力可表示为：

(11)

式中BT为体积函数.

经推导，可得式(12)所示的总体控制微分方程

(12)

假设一个单元中的温度变化极小，忽略高阶无穷小项，并将式(9)代入式(12)，方程可最终简化为：

(13)

2 有限元离散化

2.1 整体离散

应用Galerkin法对方程(13)进行有限元离散化计算.经推导，可得：

(14)

将其写成矩阵形式：

(15)

式中

对于每一个单元，有

(16)

上述方程为非线性方程，可以采用牛顿迭代法求解.

2.2 流体压力场

一旦温度场T(x,y,t)在一个给定的时间t处建立后，可以计算出流体压力场Pl和冰压力场Pi，将式(3)写成二维形式得到：

(17)

将式(17)代入式(6)并进行整理可得：

(18)

对式(18)应用Galerkin’s方法得到有限元方程：

(19)

式(19)可写成式(20)所示的离散形式

ΔtQ/Pl=-(ΔtU/T+R/ΔT) ,

(20)

其中

(21)

可以采用牛顿迭代法求解，流体压力Pl可以由式(20)计算出来.

2.3 冰压力场

研究表明，Claperon方程偏高估计了冰压力值，例如，当温度为-5 ℃时计算得出冰压力Pi=5.5 MPa，为了得到更合理的值，采用文献[20]的修正Claperon方程，即Pl=1.091Pi或者Pi=0.9166Pi.

由式(10)及式(11)可以得出由冰/流体压力导致的荷载，如果将此荷载施加至有限元模型，则可以得到由于热传导及水、气迁移引起的相应的位移和应力场.

3 数值实例验证

研究冻结壁温度变化特征和形成规律的数值解法的主要优点是其能用于比较复杂的情形，能求解分析解法所不能解决的大量导热问题.随着计算机技术的发展和应用，数值解法解题的范围、规模、速度和精确度有了很大的提高.为验证本文模型的实际效果，在ANSYS中建立单管冻结的数值模型.

3.1 参数选取与建模

模型为一圆形冻结单管，直径89 mm，管外部土体半径为2000 mm，冻结管在土体圆心位置，土体初始地温为18 ℃，开始冻结后，从冻结管中产生源源不断的冷量，冻结管的放热系数即热流为-267 W/m2，冻结管壁温度经盐水冷冻至-28 ℃，持续时间为3 630 000 s(约42 d).材料参数还包括以下内容：

(1) 对于冻土及未冻土可以赋予不同的材料属性值，如密度、比热、导热系数.

(2) 对于土体结冰释放的潜热可以在软件中通过赋予材料的焓值来实现.

参数具体取值如表1.其中土体热交换系数50 W/(m2·℃)，空气热交换系数10 W/(m2·℃).

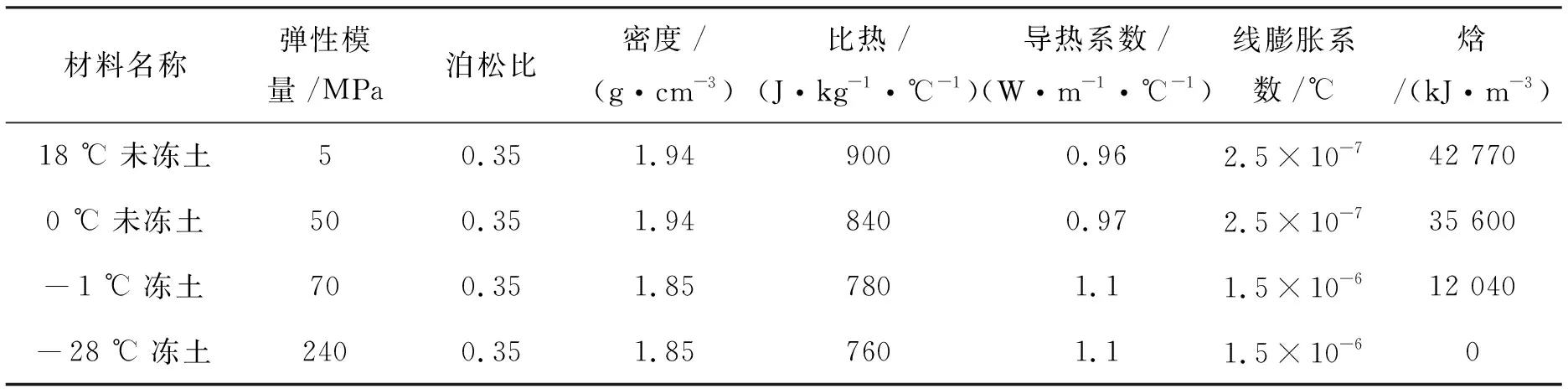
表1 各参数取值表Tab. 1 The parameter values

3.2 ANSYS建模与计算结果

ANSYS程序中土体采用PLANE13热力耦合直接法分析单元.用自带的APDL语言将所推导的三场耦合理论通过用户自定义模块输入进去进行计算.整个冻结过程中，一些参数随温度、压力、时间改变，因此要在ANSYS中建立表Table输入.

3.3 数值模拟结果分析

将ANSYS结果(如图1-图6)与实际工程对比可知：

(1)冻结温度场较为吻合，最终冻结壁厚度约1.5 m，与同条件实际工程效果较为一致，ANSYS计算结果不均匀，温度梯度跨度较大，计算精度有待于进一步提高.

(2)冻结壁径向应力受拉最大为0.39 MPa，发生在冻结管周边，受压最大为0.2 MPa，发生在冻结壁周边.而同条件下实际工程冻结土体监测结果为受压最大为0.4 MPa，基本吻合.

(3)冻结壁剪应力最大为0.36 MPa，最小为-0.27 MPa，分布不规律，实际工程中难以监测剪应力数值，故无法对比，但其值均在冻土抗剪强度指标(1.0 MPa左右)之内，未发生破坏.

(4)胀位移最大为4.15 cm，比实际工程同条件下联络通道冻结土体监测结果大，这是因为实际工程是多管冻结，且有外在约束，荷载较多，冻胀量应比简化条件下的单管理论计算小，本模型边界条件有待进一步优化.

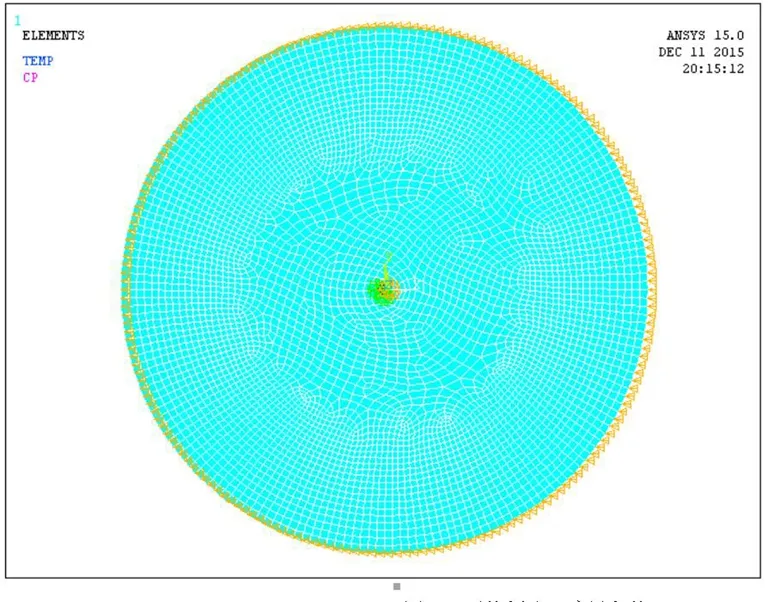
图1 网格划分及边界条件Fig. 1 Mesh generation and boundary conditions

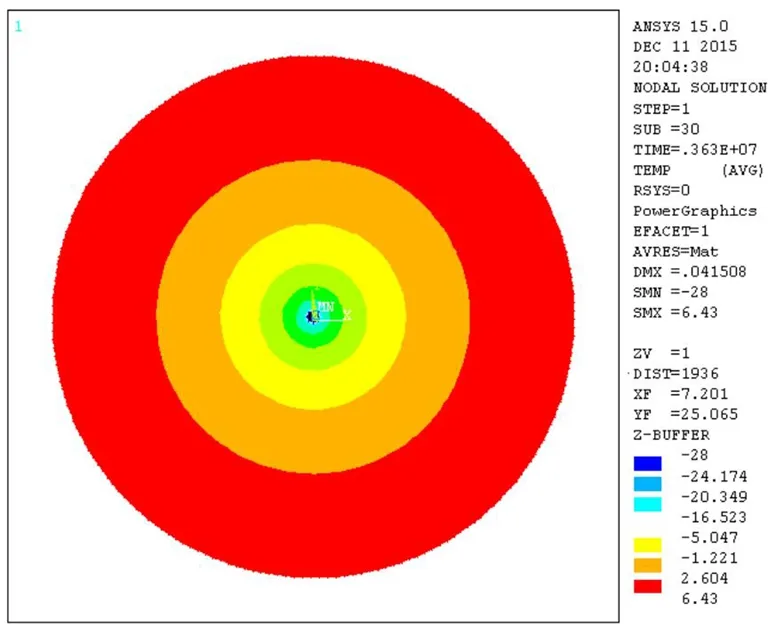
图2 温度场Fig. 2 Temperature field

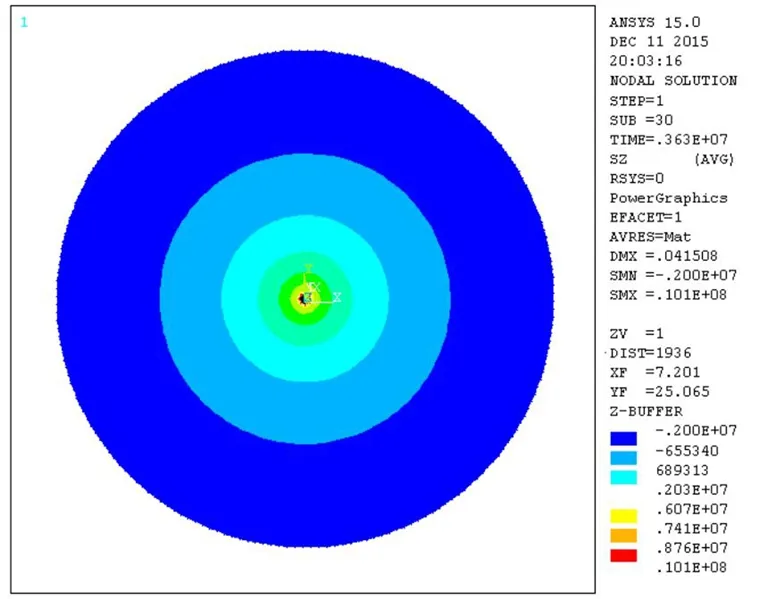
图3 Z向(径向)应力Fig. 3 Z-stress

图4 第三主应力Fig. 4 The third principal stress

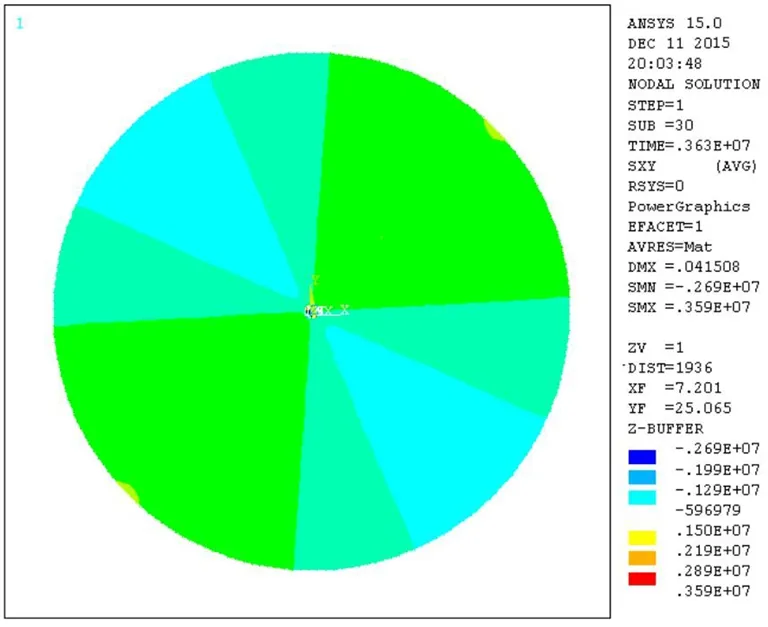
图5 剪应力Fig. 5 Shear stress

图6 冻胀位移Fig. 6 Frost heave displacement

4 结论与展望

推导了考虑水-热-力耦合的单管冻结理论计算公式，用ANSYS数值软件对某算例进行计算并与实际工程进行对比分析.结果表明：计算结果与实际工程监测结果基本吻合，偏差都在解析解及实际工程变化范围内，考虑到土体冻结工程本身也是一种不确定问题，难以取得准确解，因此，推导的理论公式计算结果是可行的，但也有以下问题需要改进，比如Clapeyron方程作为非饱和正冻土在非稳定场作用下的水分迁移的理论依据造成的计算误差问题、土体各种参数随环境条件变化问题、理论公式数值模拟过程中的优化算法问题等，这也是下一步研究努力的方向.