基于多孔介质理论的径向非均质饱和土中管桩的扭转振动

闫启方，刘林超，牛洁楠

(信阳师范学院 建筑与土木工程学院，河南 信阳 464000)

0 引言

桩基在施工和使用过程中，除了要承受水平和竖向动态荷载的作用外，在地震、动力机器等作用下通常也承受扭转动态激励的作用，所以近几十年来不少学者围绕桩基的扭转振动问题进行了相关的研究，如NOVAK等[1]基于平面应变模型研究了简谐扭转动态荷载作用下成层土中单桩的瞬态扭转振动;RAJAPAKSE等[2]借助虚拟桩模型研究了半空间中桩基的扭转振动问题；张智卿等[3]基于Biot饱和土理论研究了三维轴对称条件下端承桩在饱和土中的扭转振动特性；WU等[4，5]基于桩土黏结模型研究了成层土中桩基的扭转振动，并在考虑施工影响的情况下研究了锤形桩的扭转振动问题；姚庆钊等[6]分别采用Kelvin黏弹性模型、三参数固体黏弹性模型和分数阶黏弹性(FDV)模型描述桩周土体的本构关系对单桩的扭转振动进行了研究.近几年来由于管桩技术的快速发展，管桩作为一种新型桩在众多工程领域得到了广泛应用，对其动态力学行为的研究也越来越引起关注，特别是丁选明等[7]、郑长杰等[8，9]、靳建明等[10]、刘林超等[11]对单相土和饱和土中管桩的纵向、水平和扭转振动进行了研究.需要指出，这些研究都是将桩周土视为均匀介质，是一种理想化的模型，没有考虑桩周土的非线性或者非均质特性，而实际工程中由于施工等原因会造成桩周附近土体刚度的变化，而导致桩周土和较远土体的性质存在差异.考虑桩周土体的非均匀性，杨冬英等[12]基于虚土桩模型研究了非均质土中桩-土纵向耦合振动；刘林超等[13-15]基于内外域模型考虑土体沿径向的非均质特性研究了群桩的纵向振动.本文将在多孔介质饱和土理论的基础上，基于Novka薄层法和多圈层法，考虑桩周饱和土沿径向的非均质特性，研究径向非均质饱和土中管桩的扭转振动.

1 数学模型与基本方程

图1为饱和土中一单根管桩，桩的顶端作用一扭转集中简谐动态荷载T(t)=T0eiωt,其中T0为动态荷载幅值，w为频率，i为虚数单位.为了研究方便，这里假设管桩的桩芯被土充满，且将桩周土和桩芯土均视为饱和土，管桩、桩周饱和土和桩芯饱和土的变形均为小变形，同时桩周饱和土和管桩、桩芯饱和土和管桩之间均完全接触不产生滑移，同时假定在动态荷载作用下桩周饱和土和桩芯饱和土均未发生液化现象，管桩的桩底为基岩且视为刚性基础.对于桩周饱和土和桩芯饱和土利用多孔介质理论进行模拟，则多孔介质理论描述的饱和土的控制方程为[16]:

(1)

其中：λS、μS为饱和土固相Lamé常数，当不考虑饱和土黏滞阻尼特性时，μS等于饱和土的剪切模量；uS和uF分别代表固相和液相的位移矢量；p代表孔隙液体的压力；sv为液固耦合系数；nS、nF代表固相和液相的体积分数，同时nS+nF=1；ρS、ρF分别为固相和液相密度.

在桩基施工时，通常会对靠近桩附近的土体有较大的扰动，而在离桩较远处的扰动很小，甚至没有，为此将桩周饱和土划分为未扰动饱和土和扰动饱和土两个区域.同时为了考虑桩周饱和土沿径向力学特性的差异，设桩周饱和土固相的剪切模量为μS(r)，且μS(r)满足如下规律：

(2)

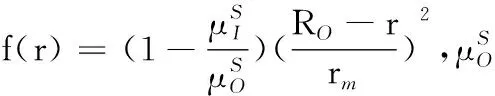
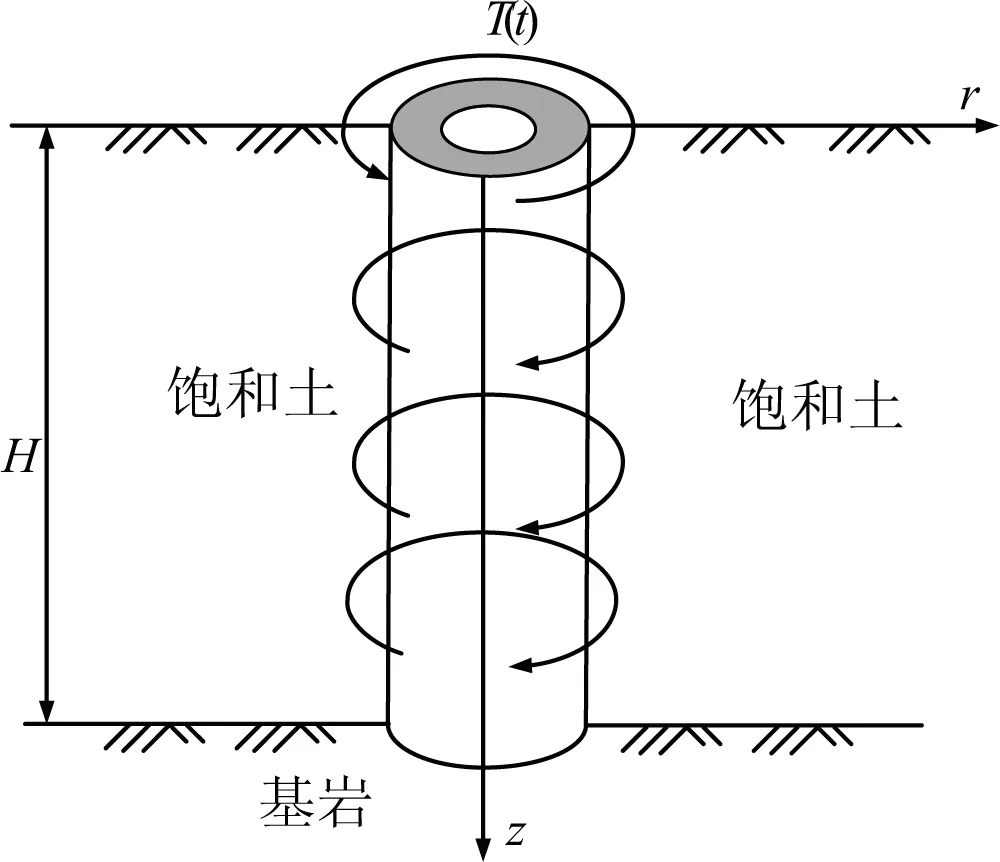
图1 饱和土-管桩扭转模型Fig. 1 Torsional interaction model of saturatedsoil-pipe pile

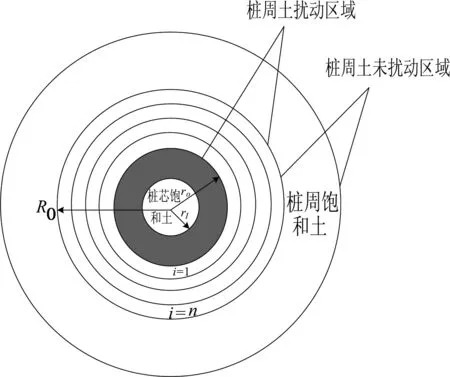
图2 多圈层模型Fig. 2 Multi-zone model

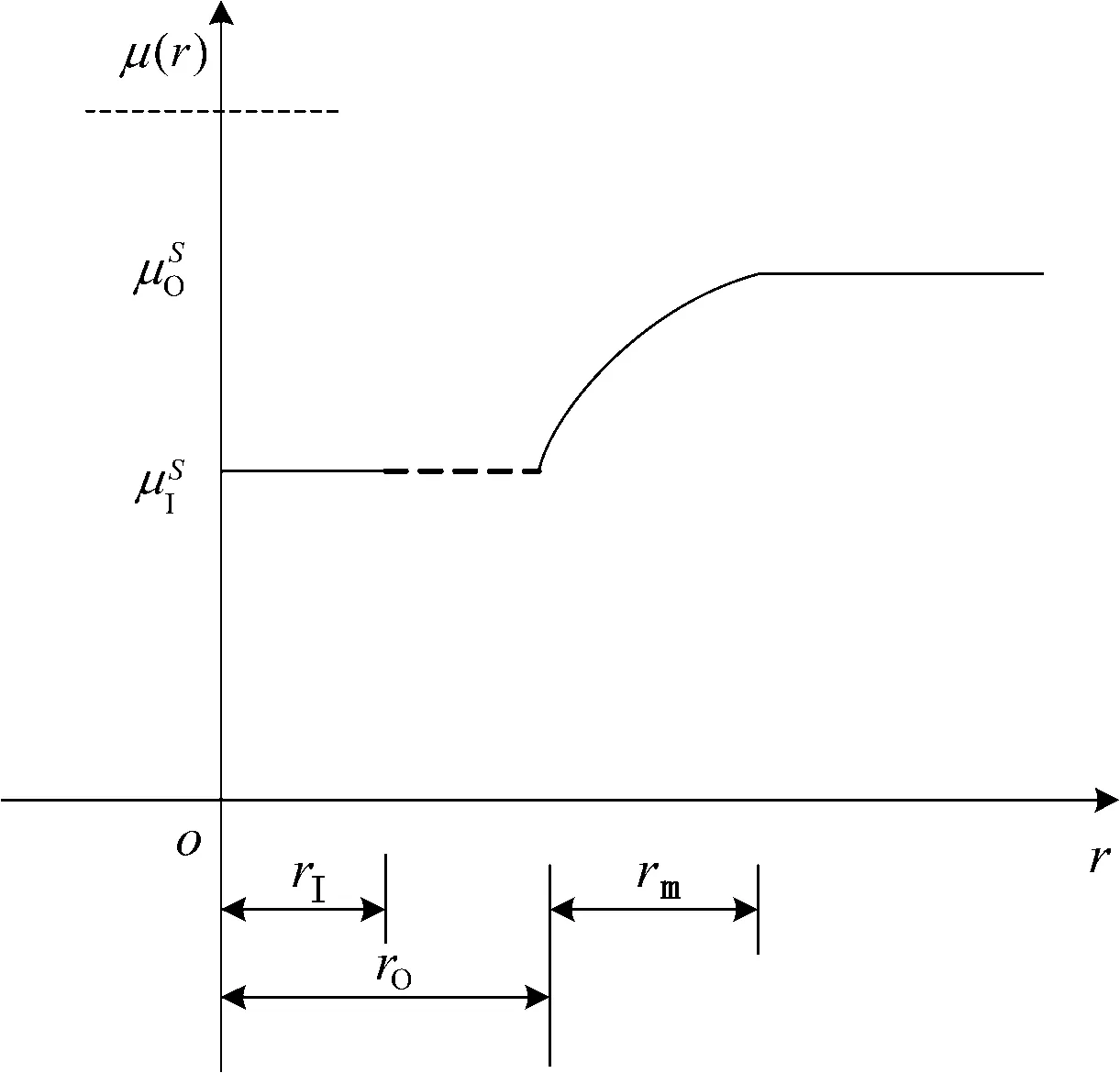
图3 剪切模量沿径向变化曲线Fig. 3 Varying curve of shear modulus along the radial

2 饱和土层的扭转动力阻抗

假设桩周饱和土和桩芯饱和土满足Novak平面假定，据此将桩芯饱和土视为由无穷多层半径为rI的薄土层组成，而桩周饱和土在竖直方向视为由无穷多带一半径为rO圆孔的薄土层组成，无论是桩芯饱和土还是桩周饱和土，在竖直方向上土层间相互独立.为了研究方便，仅考虑饱和土层的环向位移，且环向位移仅是坐标r的函数，由方程(1)，考虑轴对称条件，可以得到桩芯饱和土层的控制方程为：

(3)

(4)

桩周扰动区域第i圈层饱和土层控制方程为：

(5)

(6)

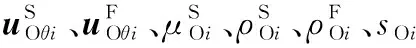
桩周未扰动区域饱和土层控制方程为:

(7)

(8)

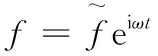
(9)

(10)

(11)

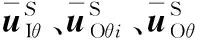
考虑桩芯饱和土、桩周饱和土未扰动区等环向位移的边界条件，则由式(9)～式(11)可得各部分饱和土层的环向位移分别为

(12)

(13)

(14)

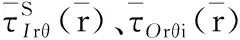
(15)

(16)

桩周饱和土外部未扰动区域对内部扰动区域的扭转剪切刚度为

(17)

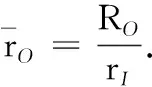
(18)

(19)

由式(18)和式(19)消去待定系数AOi、BOi可得KOi和KO(i-1)的递推关系为

(20)

这里，

考虑桩周饱和土内扰动区域各圈层之间和外部未扰动区域的连续性边界条件，则可以得到第n圈层外边界处扭转剪切刚度KOn和外部未扰动区域对内部扰动区域的扭转剪切刚度KOO，考虑扭转剪切刚度KOi和KO(i-1)递推关系式(20)，最终可以得到桩周饱和土对管桩的扭转剪切刚度KO0，再考虑桩芯饱和土对管桩的作用，可以建立径向非均质饱和土-管桩的扭转振动方程.

3 径向非均质饱和土-管桩扭转振动求解

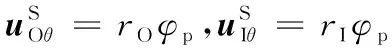
(21)

式中:

考虑由于桩底与基岩完全接触，可以建立无量纲化后的边界条件为:

(22)

(23)

4 算例对比与讨论

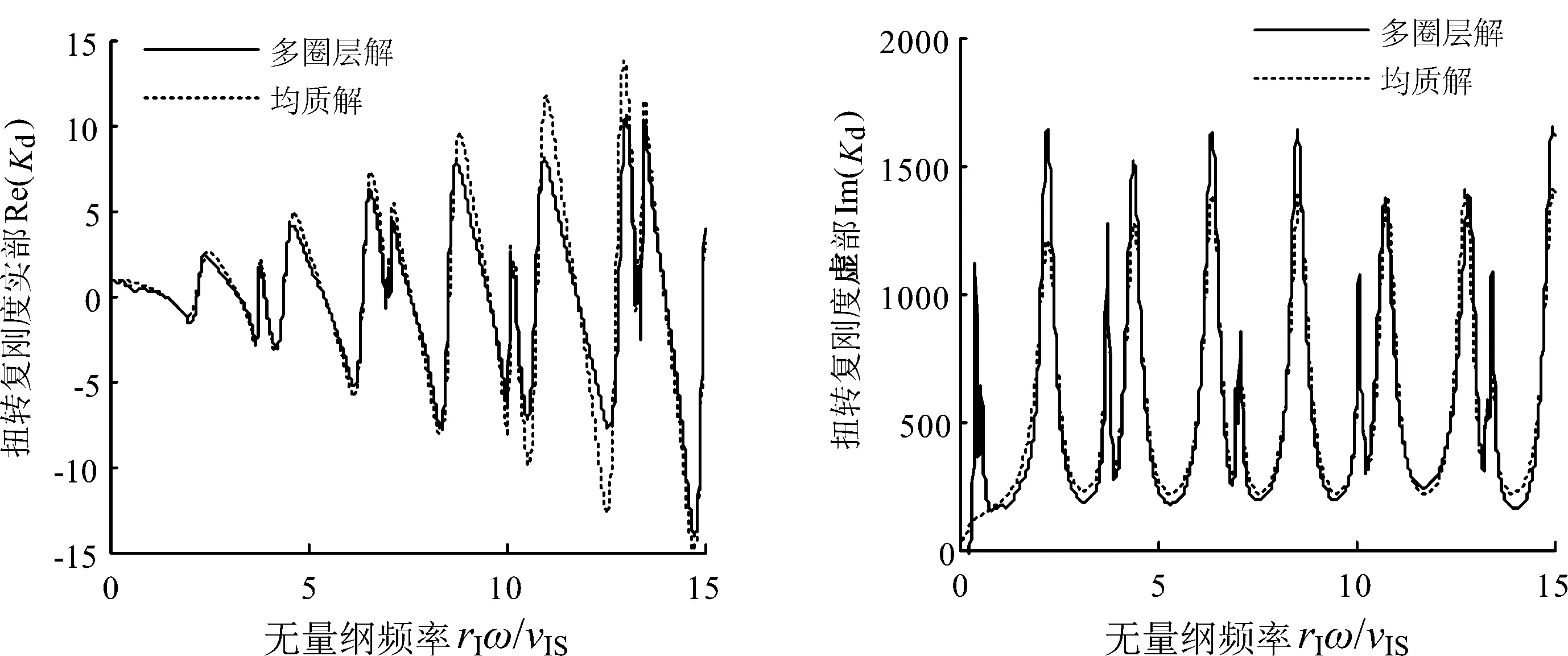
图4 扭转复刚度多圈层解和均质解对比Fig. 4 Comparison of pile torsional complex stiffness between multi-zone solution and homogeneous solution

假设桩周饱和土各圈层的液固系数相同，其与桩芯土的比值SOi对扭转复刚度的影响也主要在曲线峰值位置(如图5)，特别是高频率的峰值处，可见在频率较高时对于径向非均质饱和土中管桩的扭转振动不应忽略液相的影响，这可能是因为高频时饱和土存在有液化的可能的缘故.图6给出了桩周饱和土未扰动区域与桩芯饱和土剪切模量比μO对径向非均质饱和土中管桩扭转振动的影响，其对扭转复刚度的实部影响较大，随着剪切模量比μO的增大，扭转复刚度的实部越小.管桩外半径与内半径比rO/rI对径向非均质饱和土中管桩扭转振动的影响最大(如图7)，很明显，随着管桩外半径的增大，无论是复刚度的实部还是虚部都将增大，这可能是因为当管桩内半径一定时，外半径增大将会增大管桩与桩周土的接触面，增大土体对管桩的约束.

图5 液固耦合系数SOi不同时扭转复刚度随频率变化曲线Fig. 5 Varying curves of torsional complex stiffness with frequency for different coupling coefficient SOi

图6 剪切模量比μO不同时扭转复刚度随频率变化曲线Fig. 6 Varying curves of torsional complex stiffness with frequency for different shear modulus ratio μO

图7 管桩外内半径比rO/rI不同时扭转复刚度随频率变化曲线Fig. 7 Varying curves of torsional complex stiffness with frequency for ratio of external radius to internal radius

5 结论

本文将桩周土和桩芯土视为饱和土，并考虑了桩周饱和土沿径向的非均质特性，研究了径向非均质饱和土-管桩的扭转振动问题，通过数值分析与讨论主要得到以下结果：(1)采用多圈层方法得到的径向非均质饱和土中管桩扭转振动的结果与将桩周土视为均质饱和土得到的结果一致，但两者在峰值处存在有差异，不应忽略桩周饱和土的非均质特性；(2)在高频时需要关注液固耦合系数对非均质饱和土中管桩的扭转振动；(3)桩周饱和土和桩芯饱和土剪切模量比对管桩扭转振动的影响主要在扭转复刚度的实部，且相对较大；(4)管桩外与内半径之比对径向非均质饱和土中管桩扭转振动的影响最大，在设计时需要重点优化管桩的尺寸.