一维准无序系统中的临界相研究*

刘天帅, 魏兴波, 高先龙

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

0 引 言

自1958年安德森局域[1]提出以来,扩展相到局域相的相变已经被广泛研究.目前,较为集中的2个研究方向是迁移率边[2-4]及多体安德森局域[3-5].单体系统相对简单,但能够反映出多体系统的部分性质,所以对于单体系统的研究仍具有重要意义.

在多体系统的无序外势里加入随机相位,计算能级差比率(定义为相邻2个能级差的最小值和最大值之比)及其平均值[6-7]是研究不同相统计规律的一种常见手段.这种方法能够在有限系统中明确区分扩展相和局域相.现有的研究结果表明,多体系统中能级差比率的统计平均值在扩展相中会呈现出高斯正交分布(Gauss orthogonal ensemble,GOE)[8],其对应的平均值〈r〉=0.530 7;而在局域相中,能级差比率则表现出泊松统计[9]的特性,对应的平均值〈r〉=0.386 0.但是在一维单体系统中,能级差比率的方法是否依然适用? 是否仍然体现出多体的统计性质? 这还是一个值得研究的问题.

在单体系统中,一维具有准无序外势的Aubry-André (A-A)模型已被证实了这样一个结论:随着无序外势强度W/t的增加,系统会经历不同的相:当W/t<2时,系统处于扩展相;当W/t=2时，系统处于临界相;当W/t>2时,系统处于局域相[10-13].W/t<2和W/t>2的情况已经被大量研究,但是对于W/t=2的情况,尤其是临界相的能级差比率,至今仍没有确切的研究结果.临界相的能级差比率是否也体现出某种统计性质?它的值是否也是确定的?这仍然有待研究.

1 模型及方法

标准的A-A模型其临界相只是一个点.为了更好地研究临界相,笔者选取如下的模型进行研究[14],其形式为

-(t+λi-1+Vi-1)ui-1-(t+λi+1+Vi+1)ui+1+Wiui=εiui.

(2)

若令t+λi+Vi=Ti,则方程对应的矩阵为

本文主要采用能级差比率的方法研究临界相性质.在准无序势Wi中加入随机相位计算能级差比率是一种研究系统局域性质常见的方法,能级差比率的定义为

式(4)中:δi= |εi-εi+1|表示相邻2个能级的能级差.在不同的相中,ri会表现出不同的统计性质,当相位为φW时,能级差比率的平均值

计算能级差比率需要计算整个系统的能级,所以本文采用对角化矩阵的方法进行数值模拟,当λi=Vi=0时,此模型为标准的A-A模型.当Wi=0时,矩阵只存在非对角线上的跃迁,此时模型变为非对角(off-diagonal)A-A模型.

2 结果分析与讨论

2.1 Aubry-André 模型

图1展示了不同系统尺寸下能级差比率的统计平均值与准无序势强度的关系.由图1可以看出, 在φW=0时,能级差比率的统计平均值在临界相、局域相和扩展相3个不同的区域差异明显.这就说明,可以在φW= 0时由计算系统的能级差比率来确定3个相的范围.同时,也可以看到临界相出现在W/t= 2 时(见图1(a)),不同系统尺寸下,临界相的能级差比率的统计平均值都具有相近的值〈r〉≈0.236.当考虑了随机相位φW的影响时(见图1(b)),在临界相区域,能级差比率〈r〉≈0.320,比0.236 稍大.随着系统尺寸的增加,系统在扩展相的能级差比率的统计平均值逐渐接近于1,与多体系统中的高斯正交分布不同,原因是单体系统中没有真正的各态历经.同时,在局域相中,能级差比率的统计平均值〈r〉≈0.380.这与多体系统的结果一致,此时能级差比率表现出泊松统计性质.而在临界相,能级差比率的统计平均值〈r〉≈0.310,有别于局域相和扩展相,是我们发现的新的统计规律.

(a)φW=0 (b)φW∈ [0,2π] 的任意随机数,随机次数n= 10 000

图1 能级差比率的统计平均值与准无序势强度的关系

2.2 Off-diagonal Aubry-André模型

平均逆参与率(用“MIPR”表示)[14]是研究局域化性质的一种手段,它能够界定局域相、临界相、扩展相的范围,其定义为

图2展示了不同公度调制和非公度调制下的MIPR.由MIPR的分布可以看出,在非对角A-A模型中,临界相的范围由公度调制和非公度调制共同决定,其范围为λ/t=1-V/t和λ/t=1+V/t.而在临界相的两侧区域,MIPR值明显低于临界相的值,可以判断出此时系统处于扩展相.图3展示的是当φV=0时,不同非公度调制强度V下,能级差比率的统计平均值和公度调制强度的关系.比较图2和图3可以发现,二者在相变点附近都具有明显的变化(图2、图3中，系统参数为：Wi=0;L=987;α=610/987;φV=0).这就说明,φV=0时,能级差比率的统计平均值的确能够用于确定临界相的范围.除此之外,还可以看到,在临界相的范围内,能级差比率的统计平均值〈r〉≈0.190,这与A-A模型临界相的〈r〉不同.说明不同模型下,同为临界相,其能级差比率的统计平均值并非一个恒定的常数.

图2 不同公度调制和非公度调制下的MIPR图3 不同非公度调制强度V下,能级差比率的统计平均值和公度调制强度λ的关系

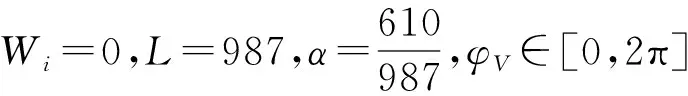
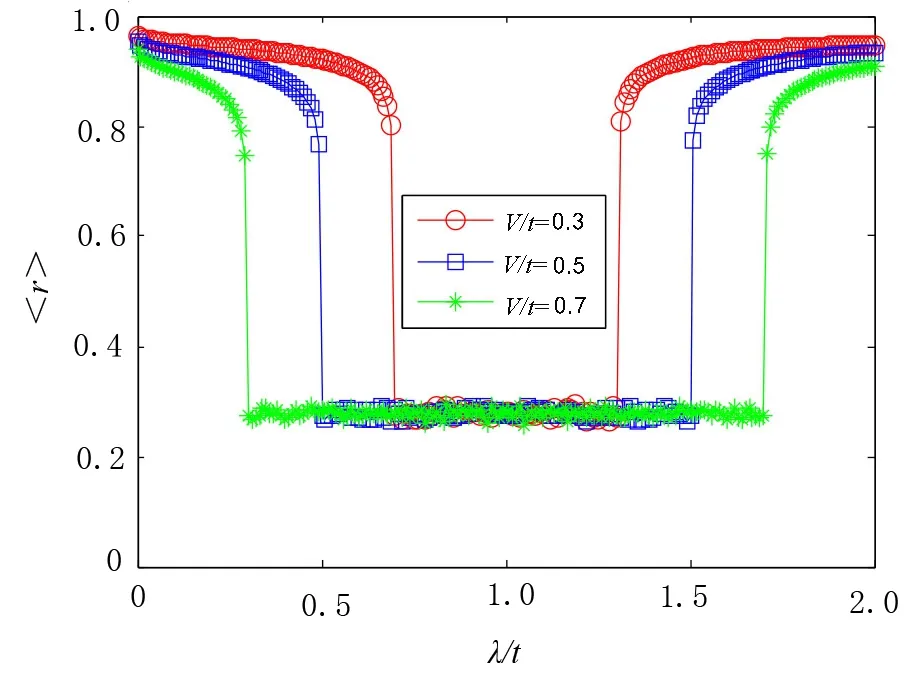
图4 考虑φV 为随机相位时能级差比率的统计平均值与公度调制的关系

波函数几率密度也可以体现扩展、临界、局域性质的不同特征.图5展示了不同公度调制和非公度调制下基态对应的波函数几率密度,系统参数为:L=987,α=610/987.图5(a)对应的能量本征值为E=-2.023 1，当选取V/t=0.5，λ/t=0.3时，相当于图2中的扩展相区域(此时λ/t<0.5及λ/t>1.5),可以看到波函数几率密度弥散到整个系统空间,故此时系统处于扩展态;图5(b)对应的能量本征值为E=-2.634 5,当选取V/t=0.5,λ/t=1.0时，相当于图2中的临界相区域(此时0.5<λ/t<1.5),可以看到波函数几率密度呈现出既非局域相的δ函数性质,也非扩展相的性质[15],故系统处于临界状态.

3 总 结

本文通过能级差比率方法研究了一维A-A模型和非对角A-A模型中的临界相,发现用能级差比率的方法可以直接确定扩展相、临界相和局域相的范围,与加入随机相位后得到的结论一致.另外,不同模型中,临界相能级差比率的统计平均值是一个不同的常数,但在同一个模型下临界相具有相同的能级差比率的统计平均值.

下一步,笔者将进一步运用能级差比率方法研究多体系统的临界相统计性质和多体局域性质.

Wi=0,L=987,α=610/987