广义混合均衡解与弱不动点的混杂迭代算法*

王元恒, 谭锦华

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

0 引 言

设X是实Banach空间,X*是X的对偶空间,C是X的非空闭凸子集,映射T:C→X的不动点集记为F(T).令f是C×C→R的双元泛函,R是实数集,h是R上的实值泛函,A:C→X*是非线性映射.广义混合均衡问题就是:找u∈C,使得

f(u,y)+〈Au,y-u〉+h(y)-h(u)≥0, ∀y∈C.

(1)

问题(1)的解集记为Ω=Ω(f,h,A).

如果式(1)中的A=0,h=0,那么此问题就等价于:找u∈C,使得

f(u,y)≥0, ∀y∈C.

(2)

问题(2)就是经典的均衡问题,其解集记为EP(f).

如果在问题(1)中令f=0,h=0,那么它等价于:找u∈C,使得

〈Au,y-u〉≥0, ∀y∈C.

(3)

问题(3)就是著名的经典变分不等式问题,其解集记为VIP(A).因此,广义混合均衡问题是一类很广泛的问题,包括了均衡问题和变分不等式等经典问题,许多学者进行了这方面的研究[1-12].文献[1]证明了临近点迭代逼近极大单调算子预解式不动点和变分不等式问题解的强收敛定理;文献[11]在一致凸一致光滑Banach空间中进一步研究了非扩张算子不动点和均衡问题解的公共元素逼近问题,建立了如下的迭代算法:

式(4)中,Π:X→C是广义投影;S是非扩张映像;φ是Lyapunov函数.则当迭代系数{αn}⊆[0,1],{rn}(n=0,1,…)满足一定条件时,由式(4)定义的混杂序列{xn}强收敛于ΠEP(f)∩F(S)x0.文献[12]又把均衡问题推广到广义均衡问题,并建立了相应迭代算法的强收敛定理.

受以上文献的启发,本文在更广泛的一致光滑的、严格凸的、具有Kadec-Klee性质的Banach空间中,研究更广义的混合均衡问题解与弱相对非扩张映射不动点集的公共元,放宽了Banach空间几何结构的限制,将非扩张映像推广到弱相对非扩张映像;并给出了一种新的变分混杂迭代算法,改进了原来广义均衡问题解与不动点的逼近格式,在较弱的条件下证明了这种新的混杂迭代序列的强收敛性.

1 预备知识

设映射J:X→2X*是由下列定义的正规对偶映像:

J(x)={f∈X*:〈x,f〉=‖x‖2=‖f‖2},x∈X.

其中,〈,〉表示对偶配对.如果X是一致光滑的,那么J:X→X*是单值映射,并且,J-1:X*→X也是一个对偶映射.J和J-1分别在X和X*的每个有界子集上是一致连续的.

定义1设X是自反光滑的Banach空间,C是X的非空闭凸子集,定义函数φ:X×X→R为

φ(y,x)=‖y‖2-2〈y,Jx〉+‖x‖2, ∀x,y∈X,

称φ为Lyapunov函数.

对于函数φ,显然有以下结果:对∀x,y,z∈X,

1)(‖x‖-‖y‖)2≤φ(y,x)≤(‖y‖2+‖x‖2);

2)φ(z,un)≤φ(z,xn)⟸⟹‖un‖2-‖xn‖2≤2〈z,Jun-Jxn〉.

为了证明本文的主要结果,还需要下列重要引理.

引理1[1]令X是一致凸和光滑的Banach空间,且令序列{yn},{zn}是X中的2个序列,如果φ(yn,zn)→0且{yn}或{zn}是有界的,那么yn-zn→0.

引理2如果X是严格凸自反光滑的Banach空间,那么对∀x,y∈X,φ(x,y)=0当且仅当x=y.

证明 充分性显然成立，故只证明必要性.如果φ(x,y)=0,那么

0≤‖x‖2+‖y‖2=2〈y,Jx〉≤2‖y‖‖Jx‖=2‖y‖‖x‖,

从而,0≤(‖x‖-‖y‖)2=‖x‖2+‖y‖2-2‖y‖‖x‖≤0,故‖x‖=‖y‖.这意味着〈y,Jx〉=‖y‖2=‖Jx‖2.由J的定义知Jx=Jy.因为J是一一映射,所以x=y.引理2证毕.

引理3[13-14]令C是光滑的Banach空间X的闭凸子集且x∈X,那么x0=ΠCx当且仅当

〈x0-y,Jx-Jx0〉≥0, ∀y∈C.

引理4[15]令X是自反严格凸光滑的Banach空间,C是X的闭凸子集,且x∈X,那么对∀y∈C,有φ(y,ΠCx)+φ(ΠCx,x)≤φ(y,x).

引理5[16-17]设T是C到C的弱相对非扩张映射,那么F(T)是闭凸的.

引理6[18]令r>0,Br={z∈X:‖z‖≤r},那么∀t∈[0,1],存在一个严格增连续凸函数g:[0,2r]→R,使得g(0)=0且

‖tx+(1-t)y‖2≤t‖x‖2+(1-t)‖y‖2-t(1-t)g(‖x-y‖), ∀x,y∈Br.

为解决广泛混合均衡问题,总假设函数f:C×C→R满足下列条件[2-3]:

(A1)对所有的x∈C,f(x,x)=0;

(A2)f是单调的,即对∀x,y∈C,f(x,y)+f(y,x)≤0;

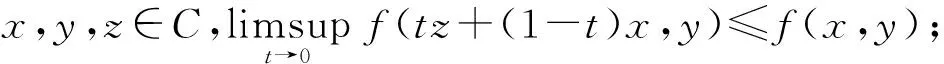
(A4)对每个x∈C,y→f(x,y)凸下半连续的.

引理7[2-3]如果函数f满足条件(A1)～(A4),且r>0,x∈X,那么

1)存在z∈C,使得对∀y∈C,f(z,y)+r-1〈y-z,Jz-Jx〉≥0.

2)定义一个映射Tr:Trx={z∈C:f(z,y)+〈y-z,Jz-Jx〉/r≥0},则下列结论成立:

①Tr是定非扩张的,即〈Trx-Try,JTrx-JTry〉≤〈Trx-Try,Jx-Jy〉,∀x,y∈X;

②Tr是单值的;

③F(Tr)=EP(f)是闭凸的;

④φ(q,Trx)+φ(Trx,x)≤φ(q,x),∀q∈F(Tr).

引理8[2]令X是一致光滑的、严格凸的、自反的Banach空间,C是X的非空闭凸子集,令h是C到R的凸下半连续的函数,假设A是C到X*的连续单调算子,令函数f满足(A1)～(A4),r>0,那么

1)对∀x∈X,存在u∈C,使得f(u,y)+〈Au,y-u〉+h(y)-h(u)+r-1〈y-u,Ju-Jx〉≥0,∀y∈C.

2)定义一个映射Kr:C→C如下:∀x∈C,

Krx={u∈C:f(u,y)+〈Au,y-u〉+h(y)-h(u)+r-1〈y-u,Ju-Jx〉≥0}, ∀y∈C.

则

①Kr是单值的;

②Kr是定非扩张的,即对∀z,y∈C,有〈Krz-Kry,JKrz-JKry〉≤〈Krz-Kry,Jz-Jy〉;

③F(Kr)=Ω是C的闭凸子集;

④φ(p,Krz)+φ(Krz,z)≤φ(p,z),∀p∈F(Kr),z∈X.

注1由引理7、引理8和Tr,Kr的定义知,Tr,Kr是弱相对非扩张映射,且Kr的不动点集F(Kr)就是广义混合均衡问题(1)的解集Ω=Ω(f,h,A).

2 主要结果

定理1设X是一致光滑的、严格凸的、具有Kadec-Klee性质的Banach空间,C是X的非空闭凸子集.假定h:C→R是凸下半连续的映射,f:C×C→R是满足条件(A1)～(A4)的函数,A:C→X*是连续单调映像,Kr同引理8,F(Kr)=Ω,T:C→C是弱相对非扩张映射且Ω∩F(T)≠Ø.令{xn}是下列迭代方法生成的序列:

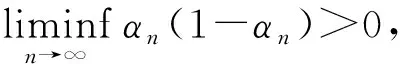
证明 分6步来证明.第1步,证明对∀n≥0,Cn是X闭凸子集.

很显然，C0=C是X的闭凸子集.由定义1的2)知

φ(z,un)≤φ(z,xn)⟸⟹‖un‖2-‖xn‖2≤2〈z,Jun-Jxn〉.

假设Cn是闭凸的,w1,w2∈Cn+1,w=tw1+(1-t)w2,t∈[0,1],有

‖un‖2-‖xn‖2≤2〈w1,Jun-Jxn〉, ‖un‖2-‖xn‖2≤2〈w2,Jun-Jxn〉,

所以用t,1-t分别乘以上述两式并相加得 ‖un‖2-‖xn‖2≤2〈w,Jun-Jxn〉,即w∈Cn+1,也即Cn+1在X中是闭凸的.所以由数学归纳法知,∀n≥0,Cn在X中是闭凸的.

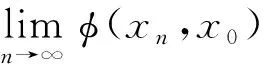
φ(xn,x0)=φ(ΠCnx0,x0)≤φ(u,x0)-φ(u,ΠCnx0)≤φ(u,x0),

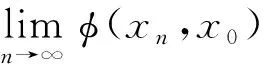
第3步,证明对∀n≥0,Ω∩F(T)⊆Cn.

显然,Ω∩F(T)⊆C0=C.假设Ω∩F(T)⊆Cn,un=Krnyn,由引理7和引理8知Krn是相对非扩张的,那么对∀n≥0,u∈Ω∩F(T)⊆Cn,可以得到

φ(u,un)=φ(u,Krnyn)≤φ(u,yn)=φ(u,J-1(αnJxn+(1-αn)JTxn))=

‖p‖2-2αn〈u,Jxn〉-2(1-αn)〈u,JTxn〉+αn‖xn‖2+

(1-αn)‖Txn‖2-αn(1-αn)g(‖Jxn-JTxn‖)≤

‖u‖2-2αn〈u,Jxn〉-2(1-αn)〈u,JTxn〉+αn‖xn‖2+(1-αn)‖Txn‖2=

αnφ(u,xn)+(1-αn)φ(u,Txn)≤φ(u,xn).

(6)

所以u∈Cn+1,从而由数学归纳法得到:对∀n>0,Ω∩F(T)⊆Cn.

第4步,证明{xn}强收敛于一点q∈Cn.

因为{xn}有界的,且X是自反的Banach空间(一致光滑空间必是自反空间),所以{xn}存在一个子序列{xni},使得xni⇀q.因为Cn是闭凸的,Cn+1⊆Cn,所以Cn是弱闭的,且对∀n>0,q∈Cn,对∀ni>0,xni=ΠCnix0,φ(xni,x0)≤φ(q,x0).

又因为‖·‖弱下半连续的,所以

因为

所以

⇀q.

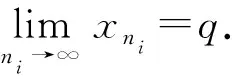
假设{xn}存在另一个子序列{xnj},使得xnj→q*.因为

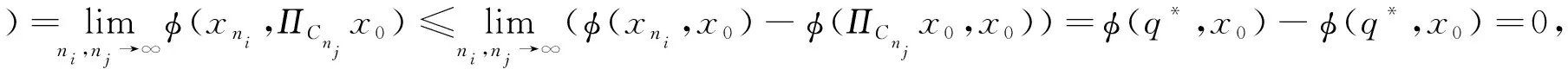
第5步,证明q∈F(T)∩Ω.首先证明q∈F(T).

因为xn+1=ΠCn+1x0∈Cn+1⊆Cn,所以当n→∞时,0≤φ(xn+1,un)≤φ(xn+1,xn)→0,φ(xn+1,un)→0.从而由引理1知,当n→∞时,xn-un→0,un→q,Jxn-Jun→0.结合式(6),对∀w∈Ω∩F(T),由引理6知,存在严格增加的连续函数g:g(0)=0,使得

φ(w,un)≤‖w‖2-2αn〈w,Jxn〉-2(1-αn)〈w,JTxn〉+αn‖xn‖2+

(1-αn)‖Txn‖2-αn(1-αn)g(‖Jxn-JTxn‖)=

αnφ(w,xn)+(1-αn)φ(w,Txn)-αn(1-αn)g(‖Jxn-JTxn‖)=

φ(w,xn)+(1-αn)(φ(w,Txn)-φ(w,xn))-αn(1-αn)g(‖Jxn-JTxn‖)≤

φ(w,xn)-αn(1-αn)g(‖Jxn-JTxn‖).

进而

αn(1-αn)g(‖Jxn-JTxn‖)≤φ(w,xn)-φ(w,un)=2〈w,Jun-Jxn〉+‖xn‖2-‖un‖2≤

2‖w‖·‖Jun-Jxn‖+‖xn-un‖(‖xn‖+‖un‖)→0.

‖Jxn-JTxn‖→0,xn→q, ‖Jxn‖→‖JTxn‖,JTxn→Jq.

又因为X是严格凸且自反的Banach空间,J-1是范数收敛的,所以Txn→q.再因为X具有Kadec-Klee性质,所以

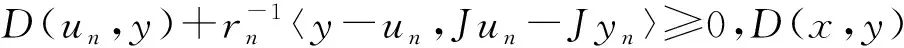
φ(q,x0)=limn→∞φ(xn,x0)≤φ(p,x0).

由ΠF(T)∩Ωx0的定义和引理2,可以推出p=q.因此,xn→q=p=ΠΩ∩F(T)x0.

定理1证毕.

3 结 语

定理1可以分别把一致凸的、一致光滑的Banach空间减弱为严格凸的、一致光滑的、具有Kadec-Klee性质的Banach空间(或者Hilbert空间),把非扩张映像T:C→C减弱为弱相对非扩张映射,把广义混合均衡问题(1)减弱为均衡问题式(2),其余条件不变,则可以得到6种不同的结果,它们分别推广或部分推广了文献[1-3,5-6,8-12]等的相关结果.