借助错例分析,改变教学策略
◇黄春丽
在一次期中考试中,我发现学生出错比较多的是几道填空题(如图1),这些都是比较具有代表性的错例。

图1
对于图1中的第5题,学生出错的原因主要是没有认真审题,对问题中的单位“1”没有分析清楚。要求女生人数占全年级人数的几分之几,这里很明显是把全年级人数看作单位“1”。很多学生没弄明白“根据男生人数占女生人数的,可以得出男生是4份,女生是5份”,不知道从何处得出全年级的份数,从而不懂这里的单位“1”如何表达。
针对这种现象,在平时的教学中,一定要加强画图策略的指导,指导学生利用画图表达题目中的数量关系,使学生养成通过画图反思自己解题过程的习惯。如果学生会画图,就可以很清楚地表达出男生和女生人数之间的关系,然后从图中找到全年级人数的份数,即男生与女生的份数之和。画图对学生理解单位“1”有很大的帮助。
图1中的第6题是找规律题。这类题经常出现在奥数中,但是在奥数中没有前面的提示。这里的提示非常清楚,算式之间的转化也很具体,目的是让学生通过观察找到规律,并利用找到的规律解决后面的题。学生存在懒惰思想,看到这么复杂的一串算式就很烦躁,不能静下心来思考如何解决这类题。
现在很多学生平时写作业依靠家长指导,在课堂上依靠老师讲解,或模仿其他同学。还有一种普遍的现象就是凑数,特别是在班里写作业时,写得慢的学生总是问写得快的,问他们最后得数是几,知道最后得数之后,就开始胡乱填写了。比如,有一道求圆面积的题,已知圆的半径是2,有些不爱思考的学生从别人那里听到答案是12.56之后,就直接用 3.14×4=12.56,也不管意义对不对,凑出这个得数就行。从这道题中,我发现,改变学生的学习态度,让学生真正学会观察,学会动脑思考,才是学生最重要的学习生长点。
还有的学生思考问题不够全面。比如,学习圆的周长之后,知道一个半圆的半径是6厘米,(如图2)让学生求它的周长是多少,有很多学生都选择了用3.14×6计算,根本就没有从问题的本质出发重新考虑解决问题的方法。所谓周长,指图形一周的长度,因此在解这道题时,我先让学生动笔把半圆的周长指出来,再用铅笔描一描这一周的长度,说一说这个图形的周长是由哪几条线组成的。可能很多学生在三年级初步认识周长时,对周长概念的认识是模糊不清的,所以到了六年级求半圆的周长时就忽略了只有封闭的图形才有周长,如果只算半圆弧的长度,怎么能够把半圆进行封闭呢?所以还必须加上下面那条直径的长度。因此,只有指导学生根据实际情况,灵活运用公式,才不会犯上面的错误,才能使学生的思维更加灵活。
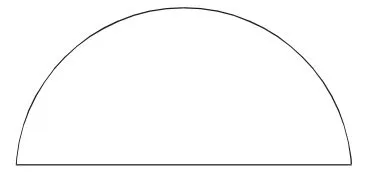
图2
图1中的第7题不仅考查学生的观察能力,还考查学生根据圆的面积公式进行逆向思考的能力。可以看出,求下面小正方形的面积,就是求半径的平方。善于观察的学生会发现:用圆的面积除以π,就可以得出这个小正方形的面积了。有很多学生纠结于怎样才能求出正方形的边长,也通过观察看出了这个正方形的边长就是圆的半径,但是并没有进一步深入思考圆的半径的平方与正方形的面积的关系。
读懂学生的错误,让我的反思越来越深刻。我深刻地感受到,分析学生的错误对改进教学具有非常重要的价值,只有读懂学生的错误,才能从根本上找到解决问题的办法和途径。

