图文信息题常见类型与指导策略
◇宋煜阳 卓芬波

图文信息题主要指采用图文结合的方式提供问题情境的题目。
常见的图文信息题,主要包括图景信息题、图表信息题、图像信息题三大类。由于构成每类题的图和文都有其自身一定的特点,所以相应的指导策略自然各有侧重。
一、图景信息题:从图文转译、信息摘录入手
所谓图景信息题,是指通过图画提供一定的数学背景,让学生结合图文中的信息解决实际问题。图景信息题素材一般来自于常见生活问题,数学生活化程度较高,关键取决于学生解决问题的第一个转化能力,即从纷乱的实际问题中收集、筛选、整理出有用的信息,从而抽象出数学问题。
在解决以图为主的图景信息题时,要引导学生学会整体观察,了解图意,将图的信息转译为文字信息,并整理所有信息,使得图文问题转化为学生相对熟悉的纯文字问题。
例1.甲、乙、丙三个修路队共同修完了一条公路。(如图 1)

图1
请你根据以上信息,算一算这条公路长多少米。
通过图文转译、信息整理,可以将例1转化为“甲、乙、丙三个修路队共同修完了一条公路。甲队完成了全部任务的一半,乙队修了240米,丙队修了全长的30%。求全长多少千米”这样的常规题。
在多幅连环图中,要善于联系图意,学会把各图之间的留白进行文字信息化处理,同时要注意观察各图之间单位、标注的变化,防止遗漏信息与看错信息。
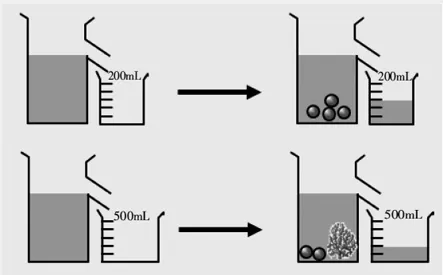
图2
例2中提供了四幅图,每行两幅图,每行两幅图之间都有箭头标示变化,在读图时,要注意每行两幅图之间的容器是相同的,但上下两行的容器大小、量杯刻度是不一致的,而将这四幅图建立联系的是“每个球的体积相同”。
以文为主的图景信息题,一般文字和数据多、题目长,阅读量大,学生容易在错综复杂的情境中不知所措。对于这类题,要指导学生耐心读题,至少分两轮读题。第一轮读题了解情境内容概要;第二轮读题要围绕问题展开分析,筛选信息并加以摘录,从而将复杂的图景信息题进行简化。
例3.绝大多数的世界贸易由海上运输完成。为了帮助减少运输船只柴油的消耗和燃料对环境的影响,工程师发明了一种风筝安装在船上,用风力来发电。
(1)船只利用风筝来行驶的一个优势是风筝在150m的高处时,风速大约比在甲板上高25%。当甲板上的风速是24km/h时,150m高度处的风速大约是多少?
(2)每升柴油的价格是5.4元,New Wave船舶公司打算配置这种风筝。据统计,配置一个这样的风筝可以减少20%的柴油消耗量。图3是New Wave船舶公司大型货船的部分信息。

图3
New Wave船舶公司配置的风筝的价格是30240000元,大约多少年后,配置这种风筝省下的油钱正好等于风筝的价钱?
例3中的大信息量、大数据对学生来说冲击很大,尤其是第二个问题,可以从不同角度理解并摘录信息、整理条件,形成解题思路。
思路1:把问题理解为“使用风筝后轮船x年的费用+风筝的价格=没有使用风筝的轮船x年的费用”这个等量关系式。相应的信息有“每升柴油的价格是5.4元”“配置一个这样的风筝可以减少20%的柴油消耗量”“不使用风筝时每年柴油消耗量:约 3500000升”“风筝的价格是30240000元”,对这些信息中的大数据进行改写、整理,明确解决问题的步骤:
第一步,没有使用风筝的轮船1年的柴油费用:5.4×350=1890(万元)。
第二步,使用风筝后轮船1年的柴油费用:1890×(1-20%)=1512(万元)。
第三步,根据等量关系式列方程解答:
设x年后,配置这种风筝后的总费用等于不使用风筝时的费用。
1512x+3024=1890x。
解得x=8。
思路2:把问题理解为“使用风筝n年后节省的费用其实就是风筝的价格”。相应的信息有“每升柴油的价格是5.4元”“不使用风筝时每年柴油消耗量:约3500000升”“配置一个这样的风筝可以减少20%的柴油消耗量”“风筝的价格是30240000元”,对这些信息中的大数据进行改写、整理,明确解决问题的步骤:
第一步,使用风筝后1年节省的费用:350×20%×5.4=378(万元)。
第二步,所求年数:3024÷378=8。
二、图表信息题:利用图表已知信息,以点带面进行突破
图表信息题一般以统计表、统计图为信息材料主体,配上相关文字构成,主要考查学生对图表中的数据进行搜集、分析和处理的能力。
图表信息题呈现形式主要有“统计图(表)+文字”“统计图+统计表”“统计图+统计图”三种组合,需要在图文之间、图表之间、多图之间进行信息切换。统计图表中的直条、图例、圆心角等都蕴含信息,解决问题时要引导学生将内隐信息外显化,并将已知信息穿插于所有图表,寻求信息关联,从而实现各个击破。
例4.向阳学校对低、中、高三个年级段近视学生人数进行了统计,绘制成如图4和图5所示的统计图。根据图中信息列式计算出中年级段和高年级段各有多少名学生近视,并将中年级段和高年级段的近视人数在图4中画出来。
例4中解决中、高年级段近视人数的突破口有两处。一是根据条形统计图中“低年级段近视人数为20”和扇形统计图中“低年级段10%”这两条关联信息,求得总人数,进而求得中、高年级段近视人数。二是根据扇形统计图中“低年级段10%,中年级段30%”信息推算出“高年级段60%”,联想到“中年级段是低年级段的3倍,高年级段是低年级段的6倍”,再根据“低年级段近视人数为20”分别求出中、高年级段近视人数。
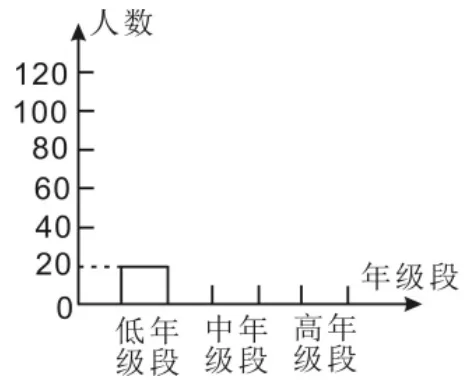
图4

图5
例4的扇形统计图里“中年级段30%”“低年级段10%”等信息都是直接明示的,但有时在扇形统计图中用直角标记来反映 “占整个扇形的25%”,隐含了“圆心角为 90°”这一信息。当然,扇形统计图还可以像例5中一样不提供任何数据,仅仅依靠圆心角在扇形统计图中所占比例的估计或估测结果作为已知信息,这对学生获取信息提出了更高的要求。
例5.下面的扇形统计图(如图6)表示给鸟喂食的混合食物配料比例。如果在混合食物中用了50克小麦,估算一下应当用多少克干面包屑。
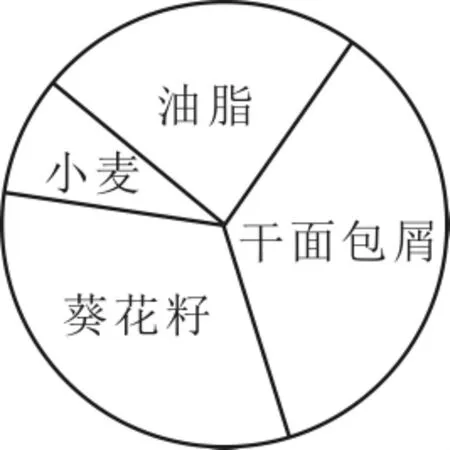
图6
三、图像信息题:利用图文对应、画图直观帮助理解
对于已知条件,图像信息题有的全部用图像呈现,有的部分用图像呈现。在图像信息解读中,既要关注变化规律的整体情况,又要关注每个时间段或部分特殊点的信息。这类题对学生的综合分析能力要求比图景信息题和图表信息题更高。
在解决图像信息题时,要引导学生借助标注,将题中的每个时间段(阶段)或部分在图像上进行划分,通过图文对照的方式分析出相应的信息。同时,要鼓励学生采用列表、画图等手段将图像中的变化情形进行直观化,帮助理解题意和分析数量关系。
例6.王叔叔从家骑车去单位上班,先走上坡路到达点A,再走下坡路到达点B,最后走平路到达单位,所用的时间与路程的关系如图7所示。下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和上班时一致,那么他从单位到家需要的时间是( )。
A.16分钟 B.21分钟 C.20.5分钟
例6是一段行程用运行图进行描述,在图中给出了上坡路、下坡路和平路的数据信息。解题时,可以结合文字信息“从家骑自行车去单位,先走上坡路到达点A,再走下坡路到达点B,最后走平路到达单位”分别给三个路段进行标注(如图8),根据横轴、纵轴含义将信息整理为表1并求出每一段的速度。
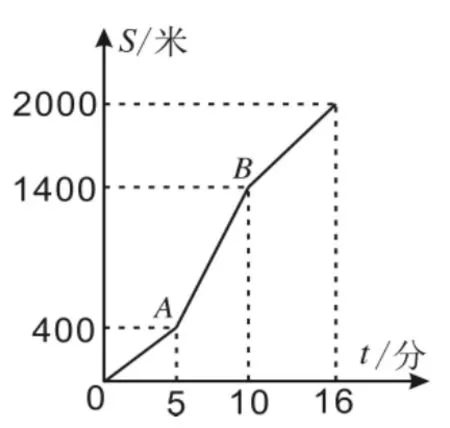
图7
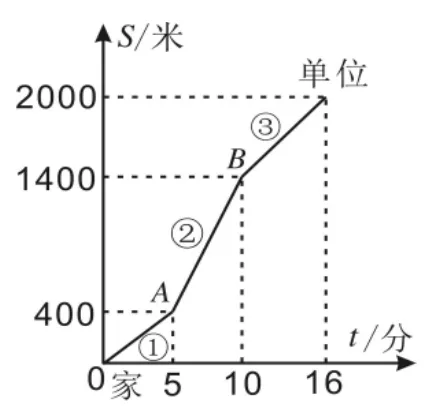
图8
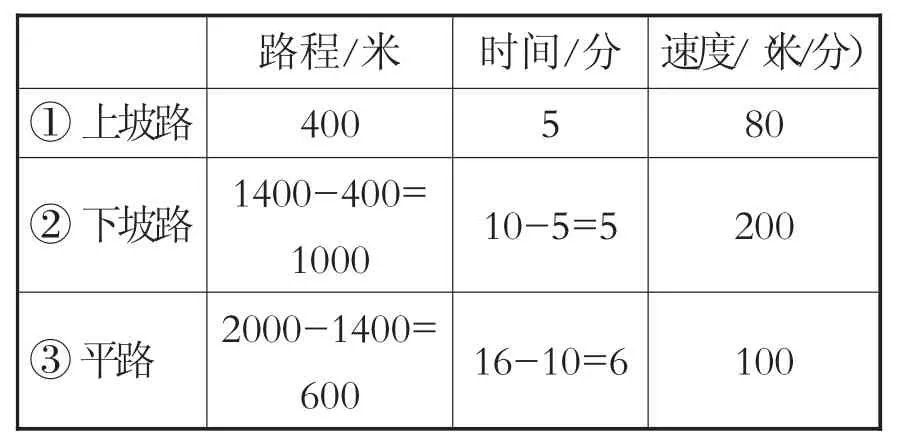
表1 上班(从家到单位)信息表
然后可以制作一张下班返回的表格,需要注意的是,上坡路变成了下坡路,下坡路变成了上坡路,进而求出返程总时间。
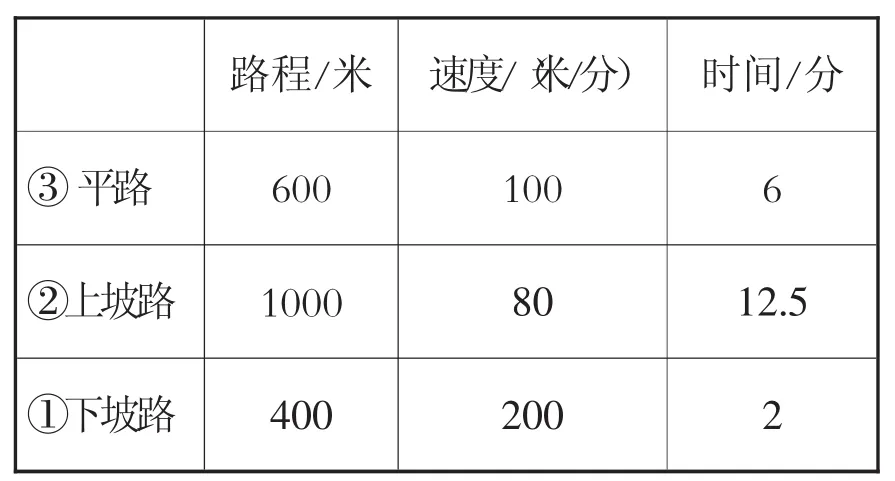
表2 下班(从单位到家)信息表
返程共需要 6+12.5+2=20.5(分),选 C。这样采用列表的形式梳理图像中相关信息,对学生来说直观、清晰,更容易理解。
例7.一个无水的长方体玻璃缸(如图9),长48厘米,宽25厘米,高30厘米。有一个水龙头从8:00开始向玻璃缸内注水,水的流量为8立方分米/分。8:03关闭水管停止注水。接着在玻璃缸内放入一个高为16厘米的长方体铁块,全部浸没于水中。玻璃缸的水面高度从注水到放入铁块的变化情况如图10所示。
(1)图10中点( )的位置表示停止注水。(从A、B、C中选择)
(2)8:03时玻璃缸水面高度为( )厘米。
(3)请列式计算,求出长方体铁块的底面积。

图9
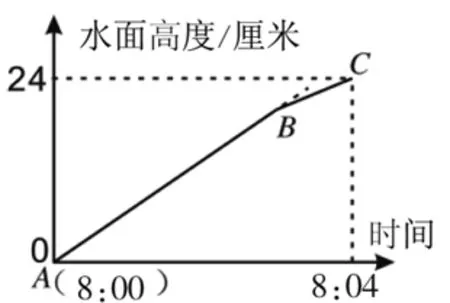
图10
例7把等积变形与正比例函数的图像有机结合,信息多、综合性强,较好地体现了函数思想和数形结合思想。解决该题时,需要加强图文信息对应、画图策略的运用。
第(1)题通过文字信息“从8:00开始向玻璃缸内注水,水的流量为8立方分米/分。8:03关闭水管停止注水”可知,共注水“3×8=24(立方分米)”,这就是水的体积。根据每分钟注水量一定、长方体容器的底面积一定,得知水面上升的高度和注水时间成正比例,通过正比例函数的图像判断出线段AB反映的就是整个注水过程,从而推断出图10中点B的位置表示停止注水。
第(2)、(3)题都涉及等积变形动态过程,在图像中仅仅给出了点C的水面高度数据,较为抽象。分析时,建议引导学生把两次等积变形的想象过程用草图画出来,使得图像信息直观化,便于分析数量关系。在自画的草图中,图11反映了第(2)题等积变形的动态图像,根据“长方体容器的长×宽×水面上升高度=水的体积”,求得8:03时玻璃缸水面高度为20厘米。
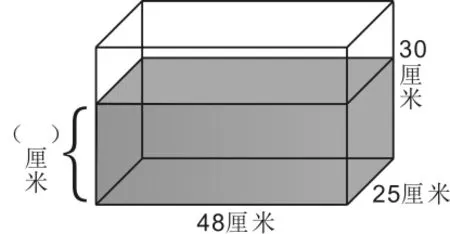
图11
再通过图11、图12两幅图的直观对比,可以看出图10中点B到点C水面再次上升的信息,并再次根据等积变形建立“第二次水面上升的体积=放入的长方体铁块的体积”的数量关系,最终求得长方体铁块的底面积。
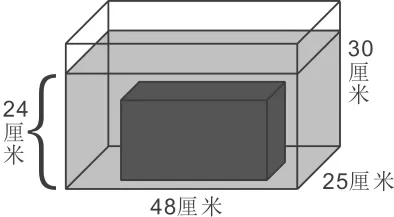
图12

