基于“预学思辨·比较建构”的深度学习

刘正妹

【教学内容】

苏教版三年级数学下册“分数的初步认识（二）”——认识一个整体的几分之一。

【学前思考】

随着新课程改革的不断深化，深度学习、意义学习已成为教育改革的共识和共同追求。向着儿童那方，怎样让我们的课前预学和孩子的课中互学、展学、评学有效衔接？怎样让孩子们课前的预学有效地导学，在孩子“学”的提升处发力，让他们带着自学中的“疑”走进课堂？怎样整合孩子的“疑”，使他们在小组互学、同座互学中感受经历不断“释疑”所带来的趣？怎样巧妙退居后台，让孩子在展学中体验汇报分享带来的乐？又怎样适时地引导追问，在引发孩子深邃的数学思考中引领他们遨游更广阔的数学空间？基于以上问题我仅以“分数的初步认识（二）”的教学为例谈谈本人的实践与思考。

【目标预设】

1.使学生在具体情境中进一步认识分数，知道把一些物体看作一个整体，然后平均分成若干份，其中的一份表示这个整体的几分之一。

2.使学生在学习用分数描述简单生活现象以及相关数量关系的过程中，进一步培养抽象、概括能力，增强用数表达和交流信息的能力。

3.使学生进一步体会分数与现实生活的联系，了解分数在实际生活中的应用，感受分数的意义和价值。

【教学过程】

一、情境交流 激趣引疑

1. 出示学生熟悉的图片（两个小朋友分蛋糕）

（1）这个情境熟悉吗？（这是上学期我们认识分数时研究的）这两个小朋友会把这个蛋糕怎么分，分的结果又是怎样的？

（2）这个二分之一是怎么来的？谁来再完整地说说？自己再轻声地说一说，这里的分母、分子各表示什么？就是两份中的一份。

2. 出示预学单中学生的疑惑（我们已经认识了分数，大家还掌握得这么好，为什么还学呢？），学完今天的内容，就能感受到了

【设计意图：在简单的熟悉的情境回顾中复习已有知识，调动学生已有的知识经验——两份中的一份就可以用表示，同时产生疑问，学得如此好为何还要学，“问题驱动”是数学教学的一条根本的教学原理。】

二、新知探究 辨析释疑

1.认识整体的二分之一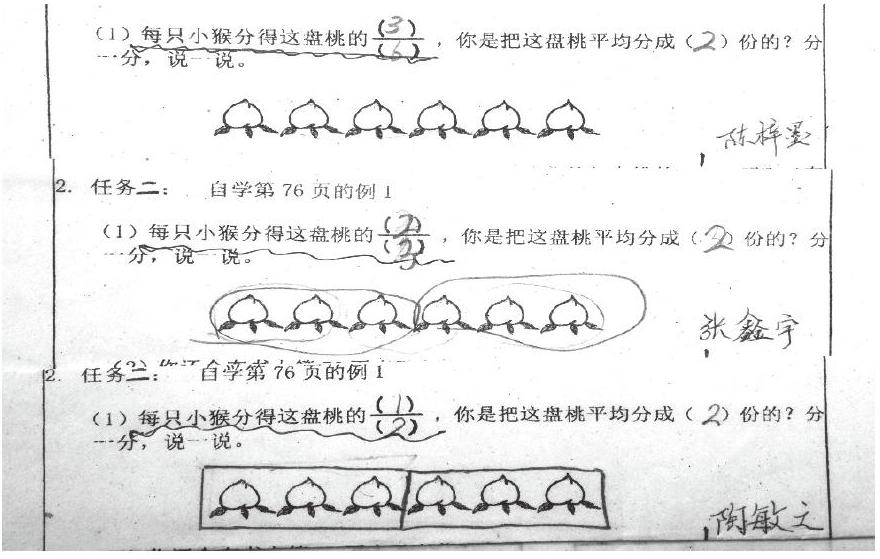

（1）今天的学习就从猴妈妈带的这一盘桃开始，把一盘桃平均分给2只小猴，问题是每只小猴分得这盘桃的几分之几？出示预学时出现的三种答案。

①你们觉得会是几分之几？结合你的预学和你的同座或小组里商量一下，并说出理由。

②想明白了吗？上来分享一下？这里的虚线表示什么，哦，每只小猴分得两份中的一份（学生上台边演示边分析）。

③为了让大家更好地分一分，分之前我们一般用一圈圈起来，把这6个桃看作一个整体，平均分成2份，就用一条虚线隔开表示什么？其中的一份就是？所以我们就说（把一盘桃平均分成2份，每份是这盘桃的）。

④竖空把刚才分桃的过程和结果完整地说一说，你来说说（教师板书）这里的每份是什么意思？哦，两份中的这一份就是，分母2表示？分子1呢？

【设计意图：结合学生预学中的错误资源，课上组织学生结合自己的操作理解进行有效的辨析，这种探索性活动经验的积累，以及学生在解决问题过程中表现出来的思维的开放性、创造性，无疑是数学教学更重要的目标。这样他们才能将问题辨得清晰、明朗。】

（2）下面的这两盘桃，我们也圈起来表示一个整体，你会表示出每盘桃的吗？

①带上嘴巴说一说、查一查，结合P76这两道题看看你预学的是否正确，有错误及时修改。

②（教师下去找两位学生，上台汇报）对于他涂的有什么想说的？（师生明确还是两份中的一份）

（3）回顧一下三次分桃的情况，拿出你的小手，圈一圈在心里说一说，有什么发现吗？

①（很会找共同点，有什么不同吗？）

为什么总个数不同，每份的个数也不同，却都可以用来表示？（这是预学单中很多同学的疑惑，哦！明白了，原来都是两份中的一份）

②如果是分10个桃、48个桃、100个，甚至更多的桃、还是这样分，你有什么想说的？

③是这个意思吗？ （不管……只要把……每份……）都把它们看作一个整体，平均分成两份，每份都是？（多了不起的发现）那这个整体可以是一盘桃，也可以是很多桃？你觉得还可以是什么？（简单的分桃中竟有这样的发现，了不起！）

【设计意图：在三次的比较辨析中找到相同和不同，使学生深刻感受同中有异、异中有同，再在拓展的延伸中使学生自然感受到本质的东西，都是把一个整体平均分成两份，每份都是这个整体的。这个整体可以是一盘桃，也可以是生活中的其他物体组成的整体，真正实现由数学向生活延伸。】

2.认识整体的几分之一

（1）还是这盘桃，小猴们想和妈妈共同分享，该怎么分？平均分成3份，每份是这盘桃的几分之几？（板书 3份 三分之一）

查一查，说一说，你是怎么分的？拿着你的预学单上来说说，并帮这个同学解决一下她的疑惑。

（2）比较例1、例2的这两次分桃，轻声地说一说，你又有什么发现？（和你的同座说一说）

（3）汇报交流，都是同样的6个桃，为什么每份的分数不同？（相同中找到了不同，不同中你还发现有什么相同？）那为什么分子又都是1呢？如果平均分成6份，每份是？（教师板书 6份 六分之一）

由此你想到了什么？（教师板书 几份 几分之一）

这里的几分之一的分母表示？分子1表示？

试一试：12个桃可以平均分成几份？每份各是它的几分之一？

师：现在请大家验证一下我们的发现。

①轻声读试一试，你读出了几个要求？（一分二填三交流）

②汇报交流，同样都是12个桃，表示每份的分数为什么不同？

③结合课件小结：把12个桃看作一个整体，平均分的份数不同，每份的分数就不同 ，每一份的个数也就不同，这一份可能是？还可能是？不管这一份有几个，但它都表示了这个整体的几分之一。

【设计意图：在学生充分认识“一个整体的”的基础上，通过自然、可信的问题情境，引导他们进一步认识一个整体的、，乃至、等，这有利于学生由特殊推及一般，水到渠成地完成对“一个整体的几分之一”的认识，同时更好地发展了学生分析推理、数学建模等核心素养。】

三、回顾整理 练习明理

1. 学到现在，之前大家的疑惑你能解释了吗？

（1）有什么不同？（以前是平均分1个物体，今天是平均分一些物体，而且在分时还把这一些物体看作了一个整体）

（2）虽有不同但也有相同之处，你发现了吗？根据学生的总结凸显出“平均分、平均分成几份，每份就是它的几分之一”，（真不错，学习就是这样，会观察更要会思考）

2.生活中这样的一个整体，有好多，就像之前说的把全班看作一个整体，平均分成两组，每组是这个整体的？平均分成4组，每组呢？那你是这个整体的？

3.好了，让我们用今天学的知识来完成课堂作业。

（1）出示第1题，学生口答。

（2）学生独立完成第2、3题后集体交流。

第2题，比较上下两幅图，总个数不同，每份数也不同，为什么都可以用来表示？横着的两个图，总个数相同，为什么所用的分数不同？

（3）出示辨析的一道题，不是平均分的，问涂色的该用哪个分数表示？

（4）看来用分数表示，首先得平均分。出示上图拆散后的图，追问现在你能表示出这些图形的几分之一？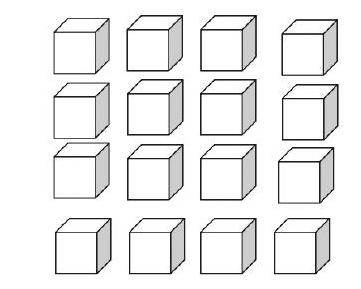

4.通过今天的认识，你又有了哪些收获，还有什么疑惑吗？

那预学中这几个同学还有这样的疑惑，你能解决吗？其实在以后的学习中这些问题都能一一化解，课后可以和爸爸妈妈还有你的好伙伴共同讨论，以后可以将你的研究成果和大家分享。

【設计意图：练习的安排既强调针对性，又注意层次性；既强调对基本的一个整体的几分之一的理解和巩固，又注意相机呈现富有一定挑战性的问题，同时穿插易错题的辨析，在学生的出错中再次突出学习内容的本质，不断提升思维水平。最后结合学生课前预学的疑惑再次将学生的学习引向深入的探究。】

四、总结

我想孩子们只有经历了课前的预学概括，课中的举例验证、释疑沟通，课尾的拓展延伸，他们才能主动从整体的视角构建知识、发展思维、提升数学素养，当然这些少不了课前教师针对学生的收获与疑惑进行的有效整合与重组.如果课上没有组织有序、存在内在关联的素材与问题串联，那学生对问题的理解就是片面的、琐碎的、肤浅的，倘若没有学生预学中的认识分歧，我们的教学任务设定无疑就缺乏合理的教学价值，也缺失学习过程中必要的对话、争论直至达成共识的丰富过程。同时我们只有了解教材的横向、纵向的体系后，对于学生的这些疑问，课上才能轻松过渡，引领他们遨游更广阔的数学空间，让孩子带着一份期待，一份向往，去憧憬着今后的数学学习。

板书设计：