蒸汽发生器非线性机理模型与动态特性分析
魏志伟, 王明春, 张雨飞, 王馥郁, 耿 健
(东南大学 能源与环境学院, 南京 210096)
回顾整个工业发展进程,传统化石燃料的使用导致了一系列的环境问题,其中雾霾、酸雨、温室效应、海平面上升等问题尤为突出,而核电作为一种可持续的清洁能源,是解决这一系列环境问题的重要途径之一。
蒸汽发生器(简称SG)作为核动力系统中连接核岛与常规岛的枢纽,其能否正常稳定地运行将影响整个核电机组能否经济安全运行[1]。笔者采用分块与集总参数结合的方法对SG进行机理建模,并对SG水位进行仿真与动态特性分析。其中,分块是对整个SG里的工质在不同阶段的不同状态分别考虑分析,主要分为一回路冷却剂单相段和二回路(包括下降段、热水段、沸腾段、汽水分离器段、蒸汽腔室段)[2]。集总参数是指针对以上划分的每一段采用集总参数的方法建立模型。
笔者采用机理建模的目的是从本质上将模型的物理结构更为清晰地展现出来,为SG水位控制提供可参考模型;同时提供一种完整的建模方式以及针对模型的处理办法。该模型能够更为直观地反映出设备运行的动态过程,有利于从根本上理解与分析SG工作原理,对SG水位控制的研究具有重要的参考价值。
1 机理模型
立式自然循环U形管SG内部具体结构图见图1。图2为分区后的SG模块示意图[3],二回路工质依次从下降段出口至热水段、沸腾段以及汽水分离器,汽水分离后饱和水回流至下降段,饱和蒸汽进入蒸汽腔室。一回路冷却剂则经过一个倒U形管与二回路工质进行传热。
1—蒸汽出口管嘴;2—蒸汽干燥器;3—旋叶式汽水分离器;4—给水管嘴;5—水流;6—防振条;7—管束支撑板;8—管束围板;9—管束;10—管板;11—隔板;12—冷却剂出口;13—冷却剂入口。
图1 SG内部原理结构图

图2 SG分区后模块示意图
1.1 一回路冷却剂单相段
SG建模时,首先作以下假设:
(1) 忽略工质与管壁之间的轴向传热。
(2) 传热管横截面上的流体特性均匀。
(3) 一回路工质在流动过程中属于单相流动,故可以看作不可压缩流体。另外,由于冷却剂温度会直接影响到二回路蒸汽湿度,温度波动幅度需要严格控制,不能变化太大,因此一回路平均密度ρp也将不会有太大波动,并且其对模型传热段的影响甚微,这里假设ρp不变以简化模型计算[4]。
图3为一回路物理模型图。

图3 一回路物理模型图
根据图3得质量平衡方程:
(1)
式中:Dp1、Dp2分别为一回路工质入口、出口质量流量,kg/s;V为一回路流通体积,m3;ρp为一回路密度,kg/m3。
由于不考虑单相流体密度ρp的变化,因此有:
Dp1=Dp2
(2)
能量平衡方程:
(3)
式中:hp1、hp2分别为一回路工质入口、出口比焓,kJ/kg;Q1为一回路工质单位时间内传给金属的热量,kJ/s。
金属蓄热方程:
(4)
式中:Tm为金属温度,℃;Q2为单位时间内金属传给二回路的热量,kJ/s;cm为金属比热容,SG合金在300 ℃时的cm取0.4~0.6 kJ/(kg·K);Mm为金属质量,kg。
Q2=K2A2(Tm-Tpj)
式中:Tp1、Tp2分别为一回路工质入口、出口温度,℃;Tpj为二回路平均温度,℃;K1、K2分别为一、二回路与金属壁之间的传热系数,取4 500~5 500 W/(m2·K);A1、A2为分别为金属与一回路、二回路传热面积,m2。
1.2 二回路下降段
假设:(1)传热管横截面上的流体特性均匀;(2)下降段中无热交换;(3)流体单相不可压缩且无热交换,假设密度不变;(4)无轴向传热。
图4为二回路下降段物理模型图。
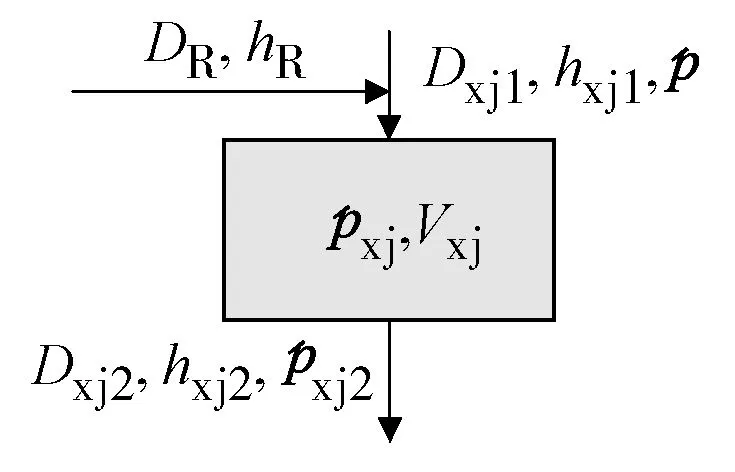
图4 二回路下降段物理模型图
根据图4得质量平衡方程:
(5)
式中:Dxj1、Dxj2分别表示二回路下降段入口、出口质量流量,kg/s;DR表示汽水分离器分离出的液态工质再循环质量流量,kg/s;ρxj表示下降段整体密度,kg/m3;Vxj表示二回路下降段流通体积,m3,Vxj=FxjL,Fxj表示下降段流通横截面积,取0.65~0.7 m2,L表示SG水位,m。
同样下降段不考虑密度变化,有:
Dxj2=Dxj1+DR
(6)
能量守恒方程:
(7)
式中:hxj1、hxj2分别表示二回路下降段工质入口、出口比焓,kJ/kg;hR为汽水分离器分离出的液态工质再循环工质比焓,kJ/kg。
压力平衡方程:
(8)
式中:p表示SG蒸汽腔室压力,也是下降段的入口压力,MPa;pxj2表示下降段的出口压力,MPa;g为重力加速度,取9.8 N/kg;ξxj为阻力修正系数,取0.9~1.1。
1.3 二回路上升热水段
假设:(1)传热管横截面上的流体特性均匀;(2)无轴向传热;(3)热水上升过程中温度变化均匀,以平均温度代替整体温度;(4)ρrs作为集总密度参数。
图5为二回路上升热水段物理模型图。
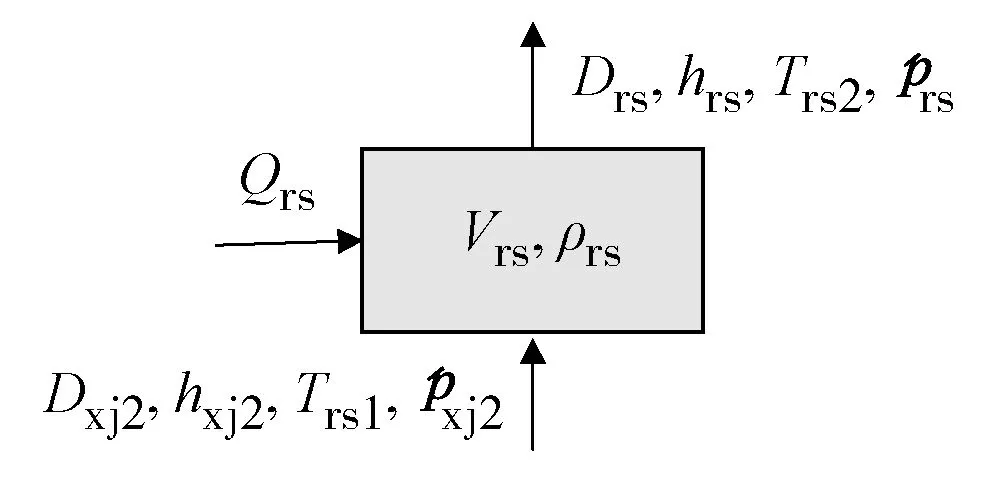
图5 二回路上升热水段物理模型图
根据图5得质量平衡方程:
(9)

能量平衡方程:
(10)
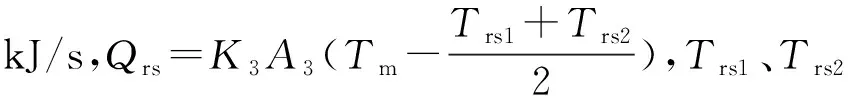
压力平衡方程:
(11)
式中:ξrs为热水段阻力修正系数,取0.9~1.1;prs表示热水段出口压力,MPa。
1.4 二回路沸腾段
假设:(1)沸腾段出口后与整个蒸汽腔室压力一致为p;(2)传热管横截面上流体特性均匀;(3)无轴向传热;(4)ρft作为集总密度参数。
图6为二回路沸腾段物理模型图。

图6 二回路沸腾段物理模型图
由于二次侧沸腾段出口压力与蒸汽腔室压力p相差甚微,因此沸腾段出口后与整个蒸汽腔室压力都可以看作为p。
由图6得质量平衡方程:
(12)
式中:Dft表示二回路沸腾段出口流量,kg/s;ρft表示沸腾段整体平均密度,kg/m3;Vft表示二回路沸腾段体积,m3。
能量平衡方程:
(13)
式中:Qft表示单位时间内金属壁向二回路沸腾传热量,kJ/s,Qft=Q2-Qrs;hft表示二回路沸腾段出口比焓,kJ/kg。
压力平衡方程:
(14)
式中:prs表示热水段出口沸腾段入口压力,MPa;ξft为沸腾段阻力修正系数,取0.9~1.1。
1.5 汽水分离器段模型
假设:(1)忽略汽水分离器前后压力变化;(2)汽水分离器效果受工况影响很小;(3)无热交换。
图7为汽水分离器物理模型图。
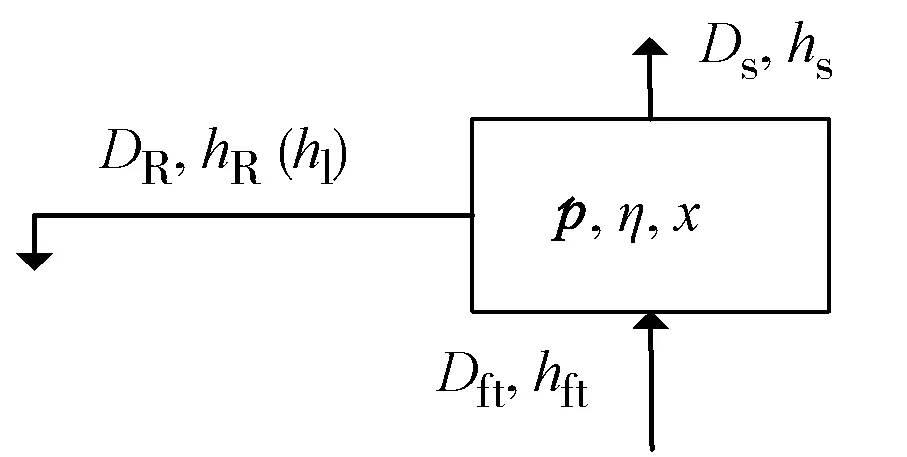
图7 汽水分离器物理模型图
由图7得质量平衡方程:
Ds=ηxDft
(15)
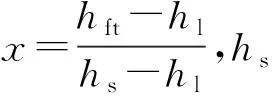
DRh1=(1-x)Dshl+(1-η)xDshs
(16)
式中:DR为汽水分离器分离出的循环饱和水质量流量,kg/s,DR=Dft-Ds;hl为对应压力下饱和水比焓,kJ/kg。
1.6 蒸汽腔室段
假设:(1)无热交换;(2)ρqs为集总密度参数。
图8为蒸汽腔室物理模型图。
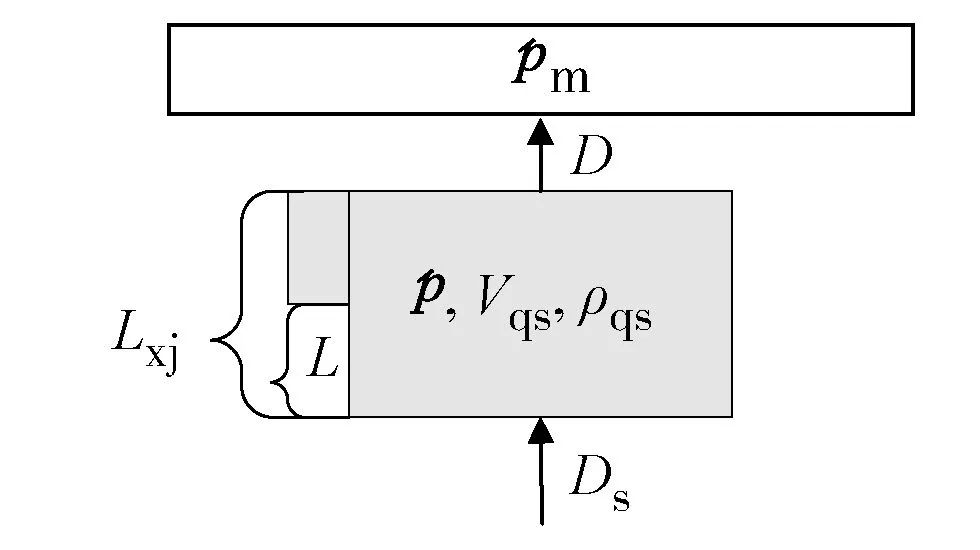
图8 蒸汽腔室物理模型图
蒸汽总体积Vzq为蒸汽腔室体积Vqs与下降通道体积之和:
Vzq=Vqs+Fxj·(Lxj-L)
(17)
式中:Lxj为下降通道总长,m。
质量平衡方程:
(18)
式中:ρqs为蒸汽腔室密度,kg/m3;D为进入母管蒸汽流量,kg/s。
压力平衡方程:
(19)
式中:pm为蒸汽母管压力,MPa;ξqs为蒸汽腔室段阻力修正系数,取0.9~1.1。
1.7 分段综合结构图
上述模型中,各段动态参数相互影响相互关联[5],这里将6段分段模型综合处理,得以下综合结构图(见图9)。
图9有6个子系统:S1表示二回路下降段,S2表示热水段,S3表示沸腾段,S4表示汽水分离器段,S5表示蒸汽腔室段,S6表示一回路冷却剂段。6个子系统之间的动态变量相互联系相互影响,共同构成完整的SG工质系统。

图9 模型各段综合结构图
2 动态模型结构处理
(20)
经过整理得隐式格式方程组,见式(21)和式(22):
(21)
(22)
3 仿真与特性分析
在上述动态模型结构中,共有6个微分方程和13个代数方程组成的隐式方程组,并有19个动态变量参数,这里采用Matlab中针对DAE微分方程组的特殊解法对其进行求解,并使输入变量做阶跃扰动。
3.1 二回路给水流量做阶跃扰动
模型在稳定运行第50 s时,二回路给水流量阶跃扰动(见图10)。此时金属壁传给二回路总热量几乎不变,导致热水段欠焓增加,工质中的气泡体积减小,水位会有一个暂时的下降,即虚假水位。与此同时,蒸汽腔室内的压力也会有所下降。但随着给水流量的增加,再循环水量增加,水位将会不断上升(见图11),腔室压力也将不断增加,而最终压力主要取决于吸热量与蒸汽带出热量,所以会达到一个新平衡(见图12),蒸汽流量虽然也会有所增加,但是难以补偿给水流量增加带来的净增量,因此水位在这种情况下无自平衡能力。所建模型与实际运行理论分析吻合,模型合理。
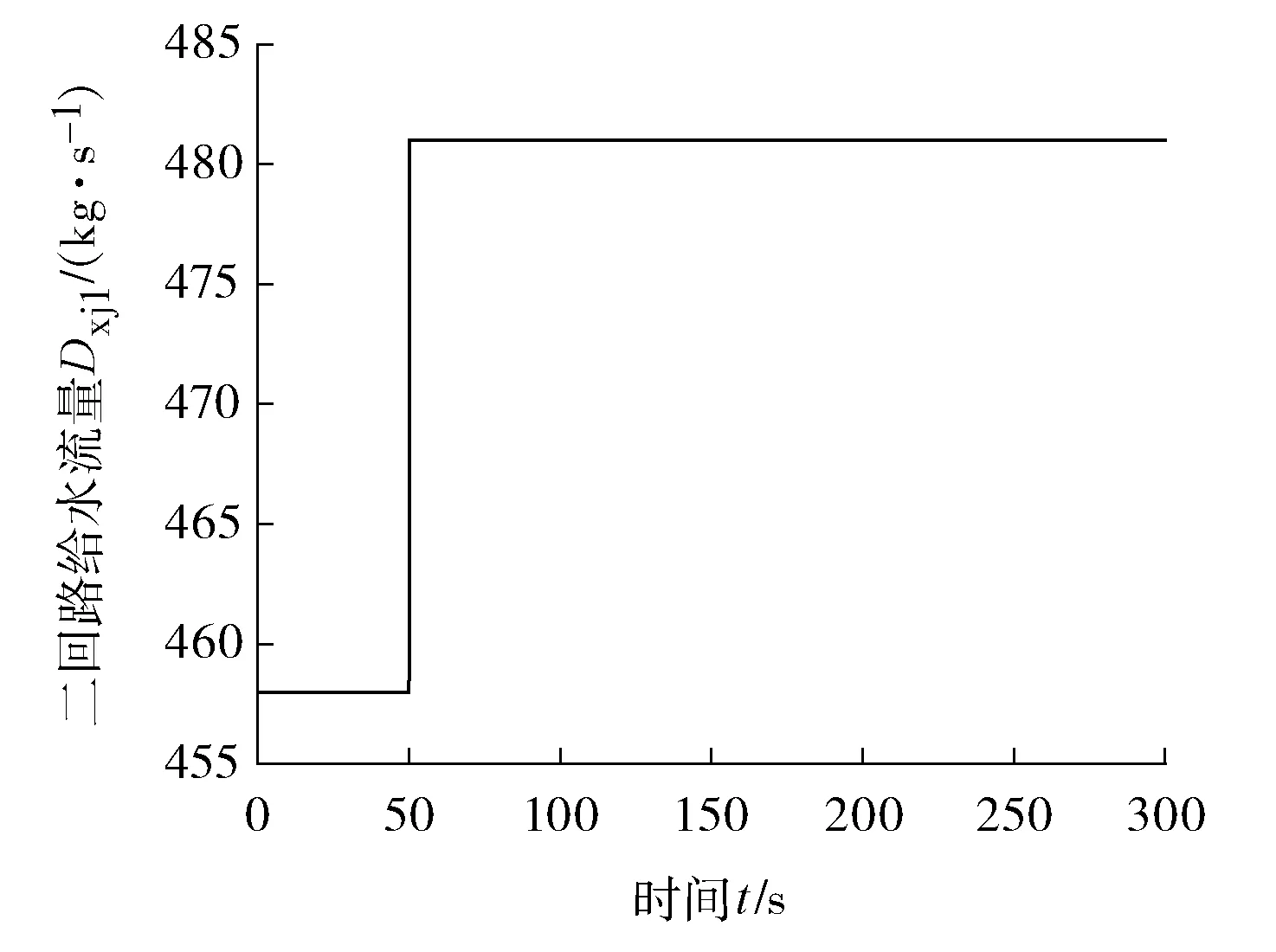
图10 二回路给水流量阶跃扰动曲线

图11 SG水位响应曲线
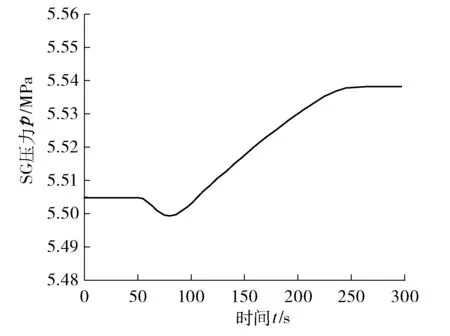
图12 SG压力响应曲线
3.2 蒸汽流量阶跃
模型在稳定运行第50 s时,使蒸汽流量阶跃扰动(见图13)。蒸汽流量在增加瞬间,SG压力理论上有一个瞬间的降低,但实际上由于流体中大量汽包以及管道中储存着大量蒸汽的缓冲作用,压力缓慢降低,并趋于新的平衡(与图14吻合);而流体中的汽包体积在压力降低时增加,导致水位有一个短暂的上升,即虚假水位,但由于给水流量与蒸汽流量的不平衡,水位会逐渐降低,并且无自平衡能力(与图15吻合)。仿真与理论分析一致,模型合理。需要指出的是:模型中并没有加控制器,因此实际上蒸汽流量是无法时刻保持阶跃变化不变的,这里只是理想状态下对模型的仿真以方便对动态特性的研究。
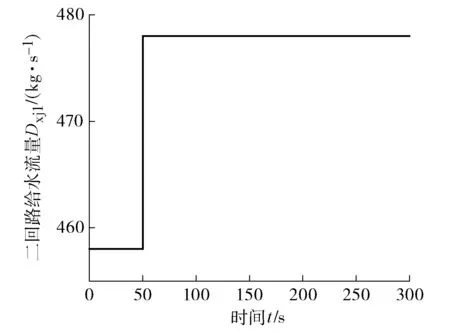
图13 蒸汽流量阶跃扰动曲线

图14 SG压力响应曲线

图15 SG水位响应曲线
3.3 一回路冷却剂温度阶跃
模型在稳定运行第50 s时,一回路冷却剂温度阶跃升高(见图16)。

图16 一回路冷却剂温度阶跃曲线
一、二回路之间的温差变大,传热量增大,二回路流体中气泡体积急剧增大,导致水位暂时的虚高,同时蒸汽产量增大,从而引起腔室内的压力增加,而工质与金属蓄热量的增加使压力趋于平衡(见图17),腔室与蒸汽母管间的压差增大,蒸汽流量增加,再循环水量随之降低,并且给水流量与蒸汽流量的差值导致水位不断下降(见图18),水位此时无自平衡能力。仿真与理论分析一致,模型合理。
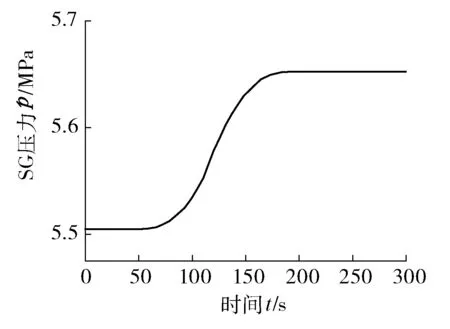
图17 SG压力响应曲线

图18 SG水位响应曲线
3.4 水位动态特性对比图
图19为二回路给水流量阶跃扰动时,所建模型与传递函数水位响应对比图,图20为蒸汽流量阶跃扰动所建模型与传递函数水位响应对比图。

图19 给水流量扰动下对比曲线

图20 蒸汽流量扰动下对比曲线
由图19、图20可见,两者趋势与数值都基本一致,再次验证所建模型合理性。
4 结语
(1) 工质在SG中经历了一系列的状态变化,尤其是二回路有受热段和不受热段,受热段又分单相与双相流动过程,因此如果直接采用集总参数进行整体考虑的话误差将会很大。笔者采用分区与集总参数结合的方式,将所有工质在SG中的流动过程精准地划分为6个阶段,每个阶段分别采用集总参数进行建模,在合理的简化假设下得到了很好的结果。
(2) 在机理模型处理的过程中,由于模型为19元高次微分代数方程组,一般的解法并不能得出准确的结果。笔者采用Matlab中针对DAE微分方程的特殊解法,对ODE解算器质量矩阵参数重新分配,并将微分代数方程变换成非线性状态空间形式,以实现微分代数方程的精确求解。
(3) 对三个输入分别进行阶跃扰动,得到的响应曲线走势都与理论分析一致,也进一步验证了模型建立的合理性与精确性。需要指出的是,二回路流量是通过调节泵转速与阀门开度等间接的方式去调控,一回路温度则受核岛中棒位、机组负荷等各种因素的影响,这里为了简化模型,采用直接扰动的方式,不影响对模型准确性的分析[6]。
(4) 建立的模型得出了较为准确的结果,提出了一个较为完整的建模方式以及模型的处理办法,并且所建模型属于“白箱”模型,能够清晰直观地展现出系统内部动态过程,有助于对SG的进一步研究,所建模型可应用于SG水位控制算法的测试与控制系统的设计中。

