平面T形钢结构的抗震性能分析
潘明明,雷庆关
(安徽建筑大学土木工程学院,安徽合肥230601)
钢结构在我国的建筑行业里发展迅猛,现钢筋用量在世界的用量排行榜里里名列前茅。目前,国家提倡建设节能省地住宅,钢结构住宅将继续增加,并且钢结构建筑在节能环保以及抗震性能上具备显著优势,因此钢结构体系的研究在我国建筑业起到了举足轻重的作用。
为了研究有、无支撑对平面T形钢结构模型的抗震影响,本文依据算例,采用SAP2000结构分析与设计软件构建以上两种模型对比分析,不难得出有、无支撑模型的自振周期、层间位移相应数据,层间位移可换算出层间位移角的数据。所得结果对比分析后,即可得出有、无支撑平面T形钢结构的抗震性能[1]。
1 模型算例
本文建立了T形钢结构框架模型,总层数为10层,总高度为35.5m,一层高度为4m,一至九层层高均为3.5m,长、短边总长度分别为38m、26m。柱距为6.0m×6.0m,2.0m×6.0m,6.0m×2.0m。屋面板选用C30强度等级,楼面板选用C30强度等级,板厚取100mm。梁、柱均采用Q235型号的工字钢,梁、柱截面尺寸分别为H400×300×10×16、500×300×12×20,结构抗震设防烈度为8度,场地类别为II类,楼板面活荷载为2.5KN/m2,楼板面静荷载为5.0KN/m2,边梁线荷载为8KN/m。模型1及模型2通过SAP2000结构分析与设计软件模拟建立,如图1、图2所示。

图1 无支撑的平面T形钢结构模型
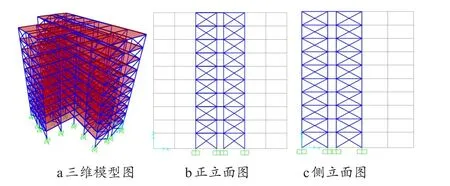
图2 有支撑的平面T形钢结构模型
2 结构模态下的动力特性分析
正文模型为T形平面不规则钢结构[2],通过模态分析了解结构每个阶次振型对应的动力特性,结构的模态分析是线性结构体系在地震中分析中的重要方法[3]。SPA2000具有两种分析结构动力性状的方法,即为特征向量法和Ritz向量法。Ritz向量法具备计算工作量小并且能生成精准结构等优点,本文模型算例采用Ritz向量法进行分析[4]。通过此方法得到有支撑和无支撑平面T形钢结构的各阶振型及周期等数据。
正文选用有、无支撑两种结构体系的有效质量系数和前12阶振型的自振周期,对比分析其抗震性能,如表1和图3所示。
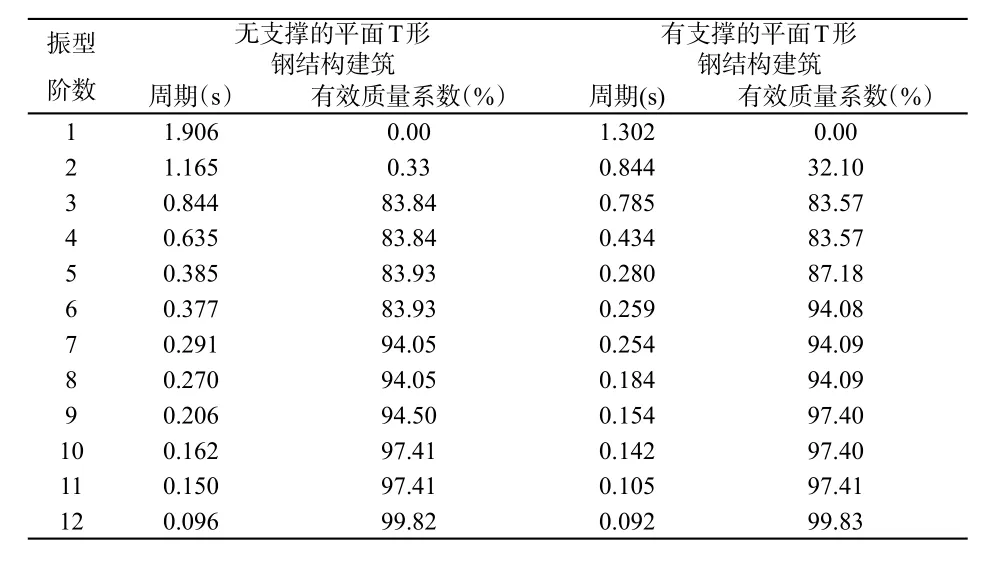
表1 两种结构模态分析下周期与有效质量系数
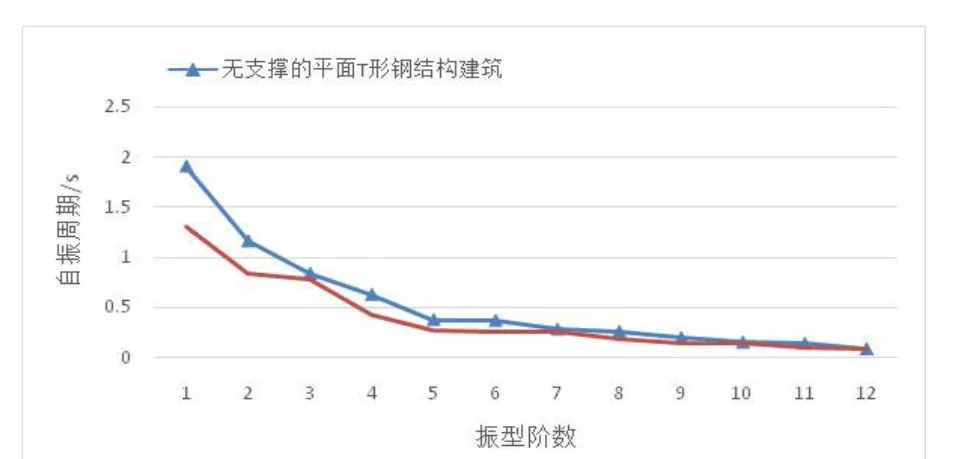
图3 两种结构的前12阶自振周期对比
由表1、图3可知:
(1)有、无支撑的平面T形钢结构模型的第一自振周期分别为1.302s、1.906s,前者的自振周期比后者的减少32%。由于无支撑的平面T形钢结构模型的刚度小于有支撑的平面T形钢结构模型的刚度,导致无支撑模型自振周期比有支撑的的大。
(2)由模态分析表明,有支撑模型很大程度上降低了模型自身的自振周期,从而有效地降低了地震对结构的影响。
3 双向振型反应谱分析
通过对有、无支撑两种结构进行X、Y方向上的双向反应谱分析,得出两种模型在X、Y方向下的层间位移和层间位移角有关数据如表2,有支撑和无支撑结构的层间位移包络图,如图4、图5所示。
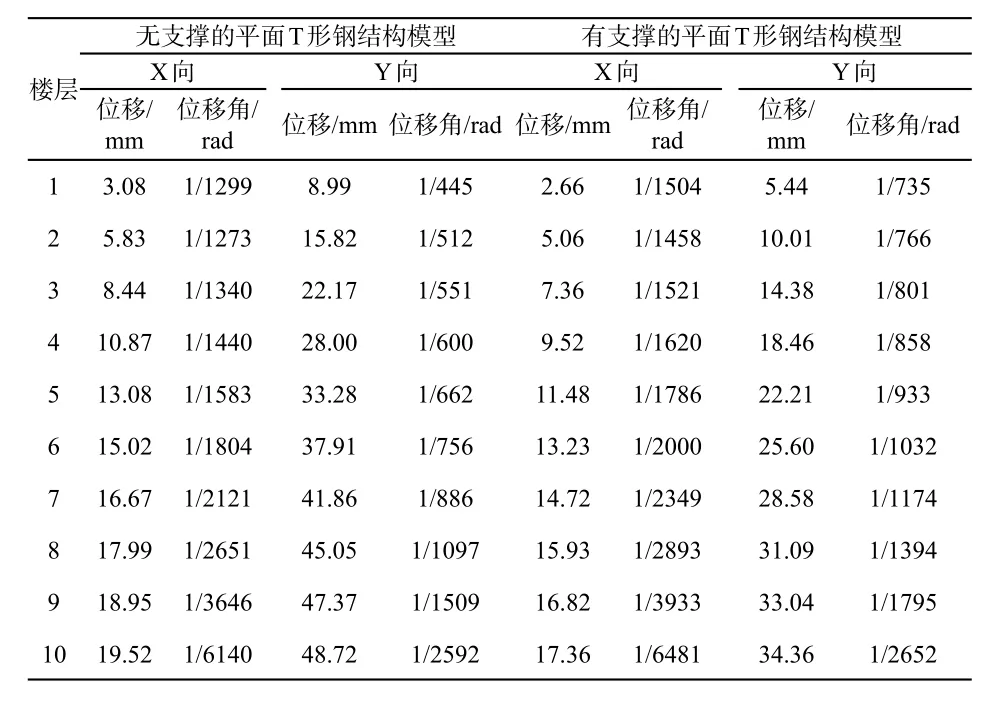
表2 双向反应谱分析下模型的层间位移和层间位移角
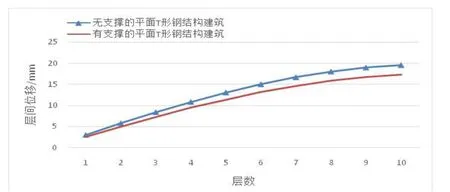
图4 反应谱分析下两种结构K向层间位移包络图
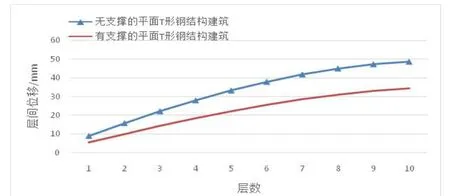
图5 反应谱分析下两种结构Y向层间位移包络图
由表2、图4、图5可知:
(1)双向反应谱分析所得数据如下所述,无支撑体系的模型在X、Y方向上产生的极值位移分别为19.52mm、48.72mm,有支撑体系的模型在X、Y方向上产生的极值位移分别为17.36mm、34.36mm。因此可得,X方向上的抗侧移刚度大于Y方向上的。
(2)无支撑体系的模型在X方向上产生的极值位移角为1/1273,Y方向上产生的极值位移角为1/445,有支撑体系的模型在X方向产生上的极值位移角分别为1/1458,Y方向上产生的极值位移角为1/735。
4 弹性时程分析
SAP2000拥有线性时程分析的功能,也具备非线性时程分析功能,结构每分每秒的响应情况和结构响应的突变情况应用恰当的积分公式换算得出[6]。本文采用三种多遇地震波,每条地震波采用的计算时长取为50S。
以上有、无支撑两种模型的楼层位移和层间位移角通过弹性时程分析所得,如表3、表4所示,绘制出的层间位移包络图,如图6-8所示。
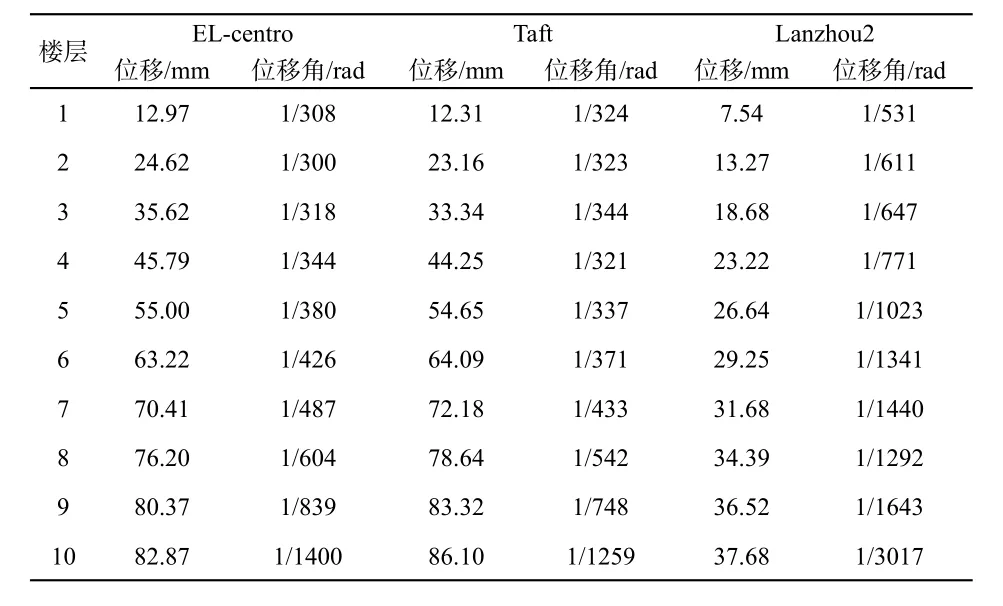
表3 线性时程分析下无支撑平面T形钢结构模型的楼层位移和层间位移角
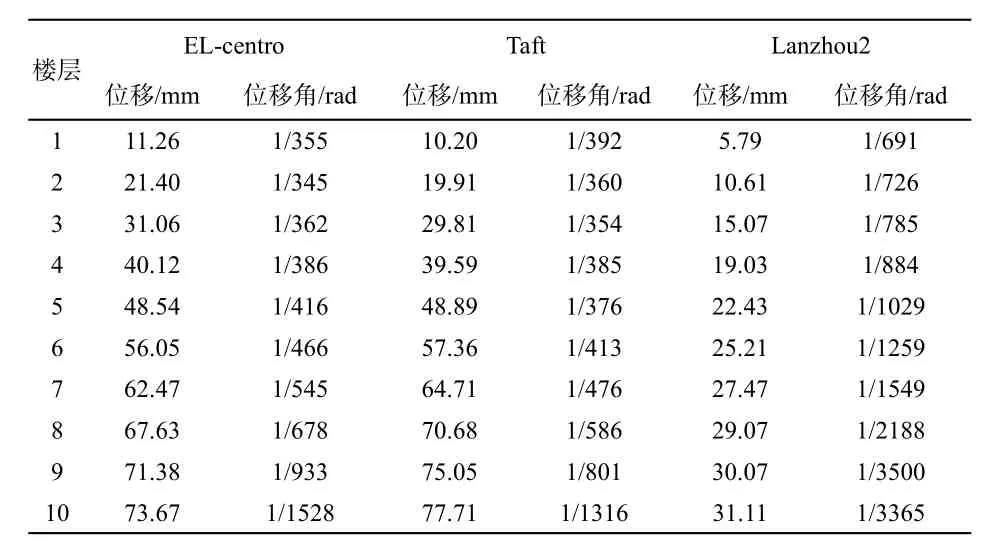
表4 线性时程分析下有支撑平面T形钢结构模型的楼层位移和层间位移角
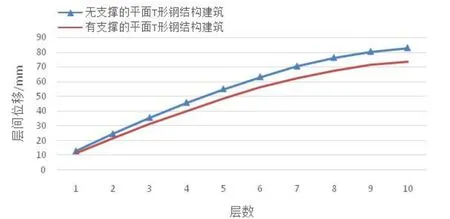
图6 EL-Centro作用下两种结构层间位移包络图
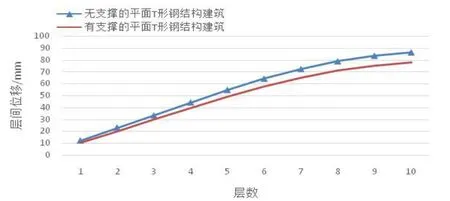
图7 Taft作用下两种结构层间位移包络图
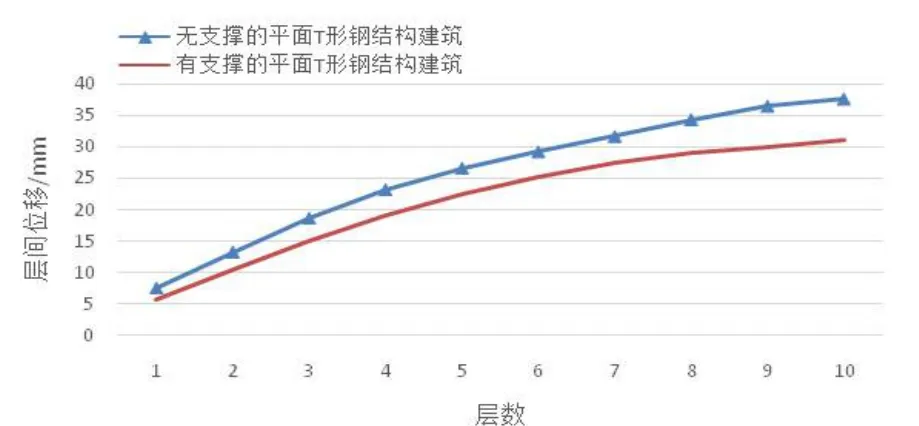
图8 Lanzhou2作用下两种结构层间位移包络图
由表3、表4、图6,7,8可知:
(1)以上两种模型的极值位移是在Taft地震波作用下所产生,即极大位移分别为77.71mm、86.10mm,Lanzhou2波作用下的顶点位移最小。
(2)在El-centro波作用下有、无支撑的两种模型顶点极值位移分别是73.67mm、82.87mm,测算后层间位移角极值分别是1/345、1/300;在Taft波作用下有、无支撑的两种模型顶点极值位移分别为77.71mm、86.10mm,层间位移角极值分别是1/354、1/321;在Lanzhou2作用下有、无支撑的两种模型顶点极值位移分别是31.11mm、37.68mm,两种钢结构模型的层间位移角极值分别是1/691、1/531,均满足规定。
3)有支撑体系的模型能有效降低结构的层间位移,从而有效起到良好的抗震效果。
5 结语
本文主要是对有、无支撑平面T形钢结构体系的抗震性能进行研究,应用SAP2000软件绘制模型,依次对结构进行自振周期分析、双向反应谱分析以及线性时程分析,对两种结构体系的抗震效果进行评估,总结得出相应结论如下所示:
(1)对两种体系模型进行结构自振周期对比分析,有支撑平面T形钢结构体系建筑很大程度上减小了结构自身的自振周期,从而有效降低地震对结构的影响。
(2)对两种模型进行双向地震作用下的反应谱分析,有支撑平面T形钢结构体系建筑抗震的层间位移比无支撑的小,计算得出的层间位移角均都小于1/250限制要求。
(3)分别对两种体系模型输入三种差异的地震波,经过线性时程分析后,两种体系模型在Taft地震波作用下产生的位移比其他两种地震波产生的位移较大;有支撑平面T形钢结构体系模型相对于无支撑平面T形钢结构体系模型而言,抗震性能更加具有优势。

