基于壳梁组合单元预应力混凝土梁非线性响应

汪 锋， 陈艾荣， 张 剑

(1. 同济大学 土木工程学院，上海 200092；2. 南京航空航天大学 航空宇航学院，江苏 南京 210016)

桥梁是公路交通的咽喉，其使用功能的优劣直接影响整条线路的畅通[1-2].以钢筋混凝土或预应力混凝土修建的各类桥梁占我国现役桥梁的绝大多数，其中T型截面梁具有构造简洁，并且适应现代化施工方法的要求，施工与使用过程中稳定性好，在预应力混凝土桥梁中被广泛采用.随着钢筋混凝土非线性有限元理论的逐渐成熟和完善[3-6]，也有越来越多关于T梁的研究成果出现：文献[7]采用具有假定弯矩-曲率关系的分层梁单元对T梁进行了非线性分析.文献[8]对当时运行约10年的沪宁高速上某锡澄运河大桥引桥(预应力混凝土简支多梁式T梁桥)进行极限状态试验研究，其桥梁极限状态(破坏性)试验研究属于现场实桥试验破坏性研究，试验对象为目前公路桥梁中应用比较广泛的桥型，具有相当的代表性；关于实桥破坏性试验研究本身，在国内尚属空白；而对预应力混凝土简支多梁式梁桥这类桥梁的现场实桥极限状态试验研究，目前在世界范围内也属首例.文献[9]结合该座预应力混凝土多T梁桥实桥破坏性试验资料，基于实体退化壳单元，研究了多T梁桥极限承载力的计算方法.文献[10]采用不同单元对T梁进行模拟，即分别采用梁单元和分层板单元模拟T梁的梁肋和翼缘板，并对T梁进行了相应分析.文献[11]进行了预应力混凝土T梁的极限承载力等力学性能的预测评估，利用混合壳单元建立了T梁有限元计算模型，并应用非线性理论对T梁进行了分析，其中T梁中预应力钢筋采用杆单元模型.文献[12]对二根跨径25 m的装配式后张法预应力混凝土简支梁静载试验，对裂缝发展模式等进行统计分析.文献[13]通过对秦沈客运专线整体多片式T梁桥的结构空间有限元分析，进行主梁横向分析系数、主梁正应力分析、桥面板的作用分析，论述了整体多片式T梁的桥面横向应力及横截面的框架效应.此外，还有学者构造不同单元分析T梁结构行为[14-17].在钢筋混凝土非线性有限元分析中，组合式模型介于分离式和整体式之间，在单元分析时，先分别求得混凝土和钢筋对组合单元刚度矩阵的贡献，再组成一个复合的单元，这种模型能在一定程度上反映钢筋和混凝土的相互作用，其有限元离散工作量和计算规模都不大，在实际钢筋混凝土结构中便于采用，如文献[18]对平面问题的组合式模型和钢筋层对体单元刚度矩阵贡献的组合式模型进行了研究；文献[19]研究了基于体单元和梁单元的组合式模型，并用此组合式单元对钢筋混凝土结构弹性阶段进行了分析.

为此，本文基于分层壳单元和梁单元计算模式，推导预应力混凝土T梁的非线性壳梁组合单元，并建立预应力混凝土T梁的非线性有限元模型.结合已有的试验成果，考证所建立的预应力混凝土T梁的非线性壳梁组合单元模型的正确性，并对其受力性能进行研究.

1 预应力混凝土T梁的壳梁组合单元

δk=[ukvkwkβ1kβ2k]T

(1)

式中：δk为实体退化壳元节点k的节点位移列阵，uk、vk、wk为节点k在整体坐标系中的线位移.

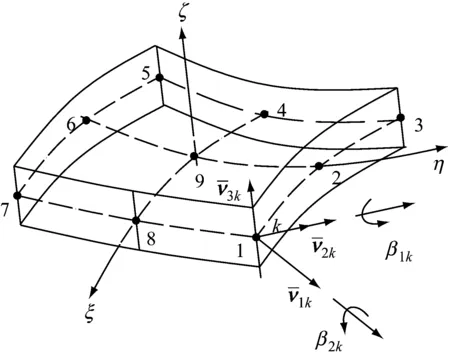
a 退化壳单元坐标系

b 节点转角位移

Fig.1DescriptionofCoordinatesystemofthedegenerateshellelementandangulardisplacementofthenode

位移场通过形函数插值可表示为[12]

(2)

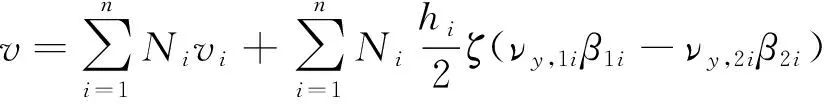
(3)

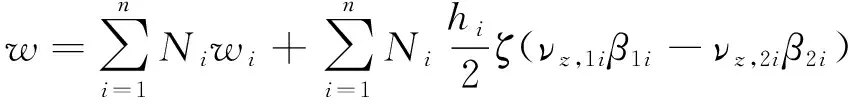
(4)

式中：u、v、w为整体坐标系下x、y、z方向的位移;n为壳元节点数;Ni为节点i的形函数;hi为节点i处壳元厚度;νx,1i为节点i的节点坐标系ν1与x轴夹角余弦值(其余类推).

基于实体退化壳得到的分层壳单元具有良好的数值稳定性[20-21].同时文献[11]中利用大变形杆单元模拟预应力筋，利用节点线位移协调推导了一种杆壳组合单元，已对相应结构进行了全过程分析，表明在预应力混凝土梁中，预应力钢筋是梁内主要受力筋，其在梁体中考虑用组合单元处理.本文利用空间梁单元模拟预应力钢筋，根据节点线位移和转角位移协调性，推导非线性壳梁组合单元.壳梁组合单元如图2所示，其中预应力钢筋用空间梁单元模拟如图3所示，预应力钢筋单元节点用A和B表示.图3中uA、vA、wA为节点A在整体坐标系下x、y、z方向的线位移，θxA、θyA、θzA为节点A在整体坐标系下绕x、y、z轴的转角位移，节点B的位移变量依此类推.

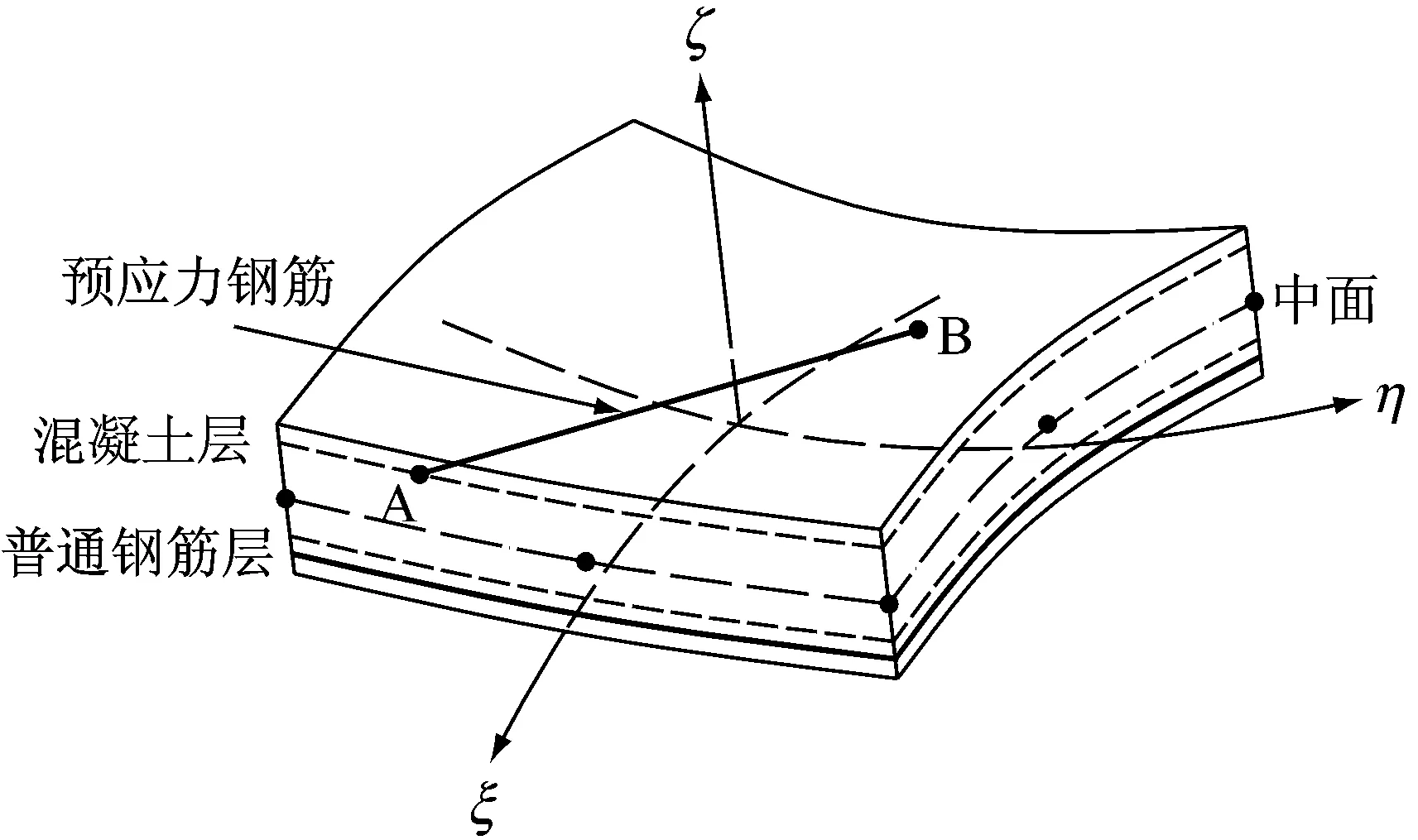
图2 预应力混凝土梁的单元模型Fig.2 Element model of the prestressed concrete beam

转角位移场通过形函数插值由式(5)～(7)表示如下：

(5)

(6)

(7)

式中：θx、θy、θz为绕整体坐标系x、y、z方向的转角位移场.

利用位移插值关系式(2)～(7)，则预应力钢筋单元的起点A和终点B线位移和转角位移可用退化单元的节点位移表示为

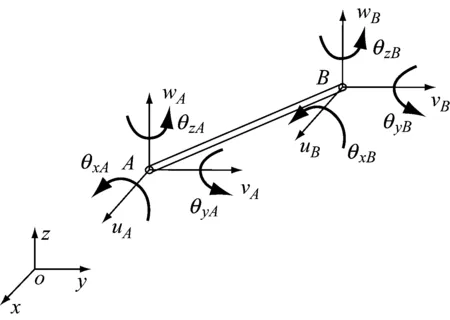
图3 预应力钢筋的空间梁单元Fig.3 Spacial beam element of the prestressed reinforcement

(8)

(9)

δS=RδC

(10)

应用虚功原理[13]，推得预应力筋单元对组合单元刚度矩阵的贡献如下:

(11)

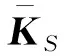
(12)

式中：Ke为组合单元刚度矩阵；m为混凝土层数，KCk为第k层混凝土的刚度矩阵；KS为普通钢筋层的刚度矩阵.

2 预应力混凝土T梁的非线性效应

2.1 混凝土的非线性描述

对于混凝土的材料非线性，考虑其屈服、强化、拉伸刚化和压碎过程.本文选用Owen混凝土双参数屈服准则和Hinton压碎准则.Owen混凝土双参数屈服准则表达式为

f(I1,J2)=(αI1+3βJ2)1/2=σ0

(13)

式中：I1为应力张量第一不变量；J2为应力偏量第二不变量；σ0为等效应力;α、β为材料参数，α取1.355，β取0.355.

Hinton压碎准则表达式为

(14)

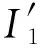
2.2 钢筋的非线性描述

本文假定普通钢筋和预应力钢筋均为力学性能是单向的理想弹塑性材料，以模拟其材料非线性特性.普通钢筋采用壳元中等效厚度的层单元考虑[13].假定每一钢筋层的力学性能是单向的，只能承受沿钢筋方向的轴向力.预应力效应的准确模拟对结构分析至关重要，本文预应力钢筋采用空间梁单元考虑[5].沿梁单元局部坐标的轴向方向，输入估算得到的有效预应力作为初始预应力，并将其处理为等效节点荷载施加于预应力混凝土梁进行结构分析.

3 非线性分析的收敛准则

收敛准则一般分为：力系收敛准则和位移收敛准则.在预应力混凝土结构非线性分析中，不平衡力常可形成一些平衡力系，使得解不能单调收敛，因此采用位移收敛准则，取

(15)

式中：δi为第i增量步的非线性方程组迭代时的收敛解，即预应力混凝土T梁第i增量步整体位移向量；δi+1为第i+1增量步的非线性方程组迭代时的收敛解；ε为收敛容差(可取为5%).

4 算例分析

4.1 试验梁资料

为研究预应力混凝土T梁的非线性受力性能，交通部第二勘查设计院进行了二根装配式后张法全预应力混凝土简支T梁的试验[12].预应力混凝土T梁尺寸如图4所示(图中,p为荷载).采用40号混凝土，预应力钢筋采用24Φ5的冷拉碳素钢丝，极限抗拉强度1 600 MPa，控制张拉应力1 200 MPa.混凝土抗压强度36 MPa，抗拉强度3.35 MPa.混凝土弹性模量36 GPa，预应力钢筋弹性模量220 GPa.6根预应力钢筋沿T梁纵向位置坐标以及普通钢筋等构造详见文献[12].

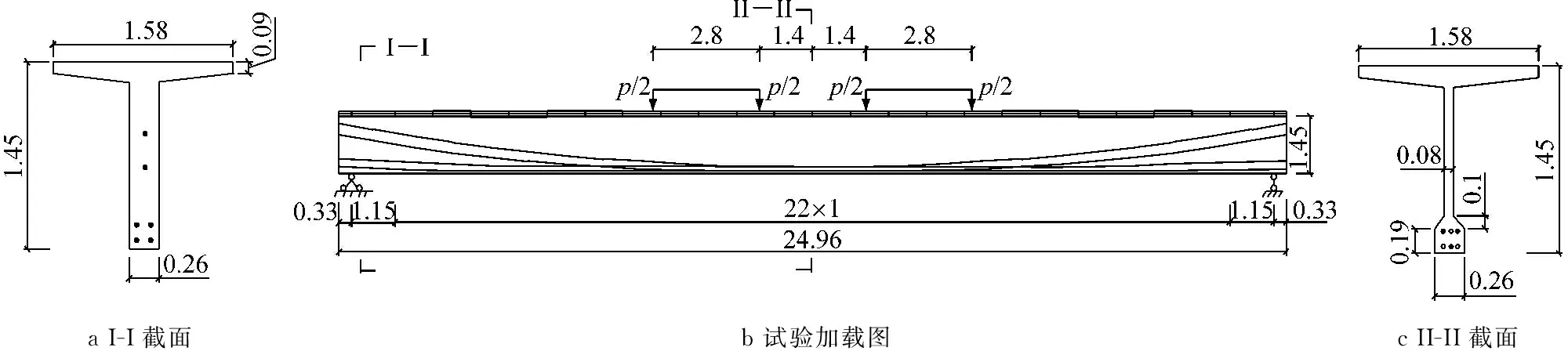
a I-I截面b 试验加载图c II-II截面

图4预应力钢筋混凝土T梁的构造及加载方式(单位：m)

Fig.4ConfigurationandloadingtypeoftheprestressedreinforcedconcreteTbeam(unit:m)

4.2 荷载挠度曲线及刚度折减规律

为进行预应力混凝土试验T梁非线性受力性能分析，建立非线性力学分析模型，共分176个单元，759个节点，其中壳梁组合单元48个，分层壳单元128个.对普通钢筋和混凝土均采用分层壳单元模拟，对预应力钢筋用壳梁组合单元模拟.由试验方法测得二根试验梁的极限承载力为1 104 kN和1 125.8 kN.利用本文的壳梁组合单元方法，计算得预应力混凝土T梁的极限承载力为1 100 kN.梁体1/4跨和跨中梁底的荷载-挠度曲线分别如图5和图6所示，典型加载步下梁的裂缝发展模式如图7所示.

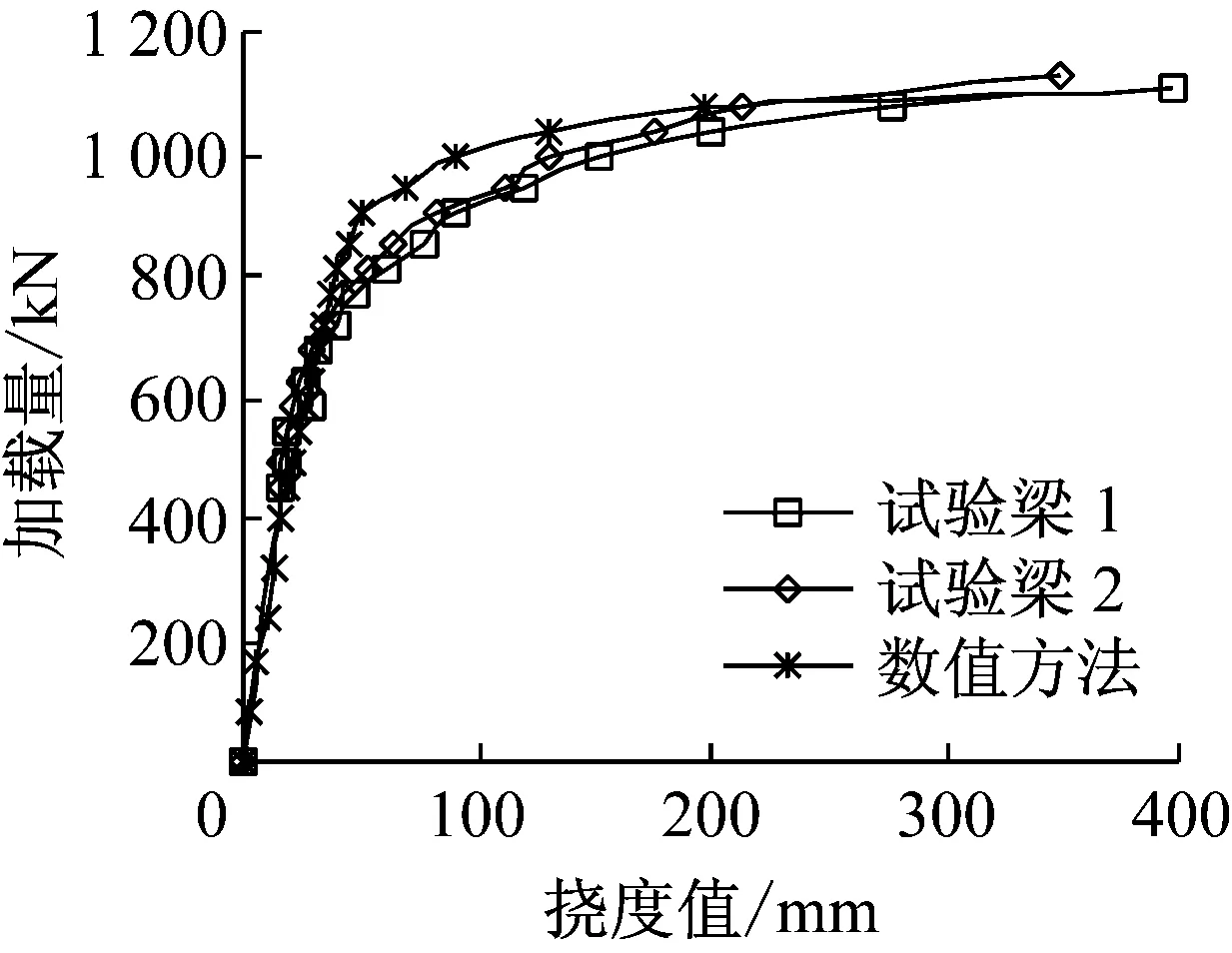
图5 1/4跨荷载挠度曲线Fig.5 loaddeflection curve of the 1/4 span

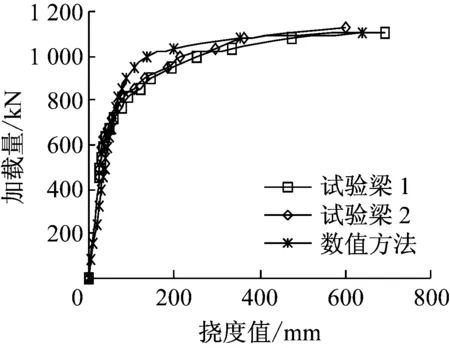
图6 跨中荷载挠度曲线Fig.6 loaddeflection curve of the half span

a 荷载步13时

b 荷载步17时

图7典型加载步下预应力混凝土T梁的裂缝发展图

Fig.7CrackdevelopmentdiagramoftheprestressedconcreteTbeamattypicalloadingstep

由图5和图6的计算结果知，本文方法与试验结果吻合程度良好，说明非线性壳梁组合单元计算方法为正确.由图7可知，本文所得混凝土简支梁梁的裂缝发展规律与已有资料相符[9、11].本文定义“刚度折减系数” ，主要描述在不同加载阶段，梁体刚度的变化情况.刚度折减系数的表达式为

(16)

式中：β为梁体刚度折减系数；pt为t时刻的加载量；st为t时刻的梁跨中挠度值；pt/st为t时刻的梁割线刚度;p0/s0为梁的初始割线刚度.由图6计算结果可知跨中刚度变化规律(刚度折减系数)见表1.

表1中，刚度折减系数18.19=(1-10.95/13.55)×100%.由表1可知，在加载初期，T梁处于弹性阶段，刚度未出现明显折减.其后随着加载量增大，T梁刚度折减系数越来越大，表明其继续承受荷载的能力越来越小.本文对预应力筋采用了梁单元处理，也可以采用层单元和杆单元模拟，这在相关成果中已得到了验证[20-21].

表1 预应力混凝土T梁跨中的刚度折减Tab.1 Stiffness reduction in the half span of the prestressed concrete T beam

4.3 预应力筋的应力重分布规律

预应力混凝土T梁典型截面的梁底预应力钢筋的应力-荷载曲线如图8所示.由图8计算结果可知，接近破坏时，跨中截面的预应力筋已达1 547.02 MPa.跨中预应力筋的应力增长速度最快，1/4跨预应力筋的应力增长速度次之，1/8跨预应力筋的应力增长缓慢，而支座处预应力筋的应力-荷载曲线基本保持水平.

本文提出“应力重分布系数”来描述不同加载阶段应力增量对相应荷载增量的变化率与弹性阶段的应力增量对相应荷载增量的变化率之比值，分析应力的变化速度.应力重分布系数表达式为

(17)

式中：η为应力重分布系数；Δpt为t-1至t时段的荷载增量;Δσt为与荷载增量Δpt为t-1至t时段的应力增量;Δp0为弹性阶段的荷载增量;Δσ0为弹性阶段的应力增量.由图8可得跨中预应力筋的应力重分布规律(应力增长率和应力重分布系数)见表2.

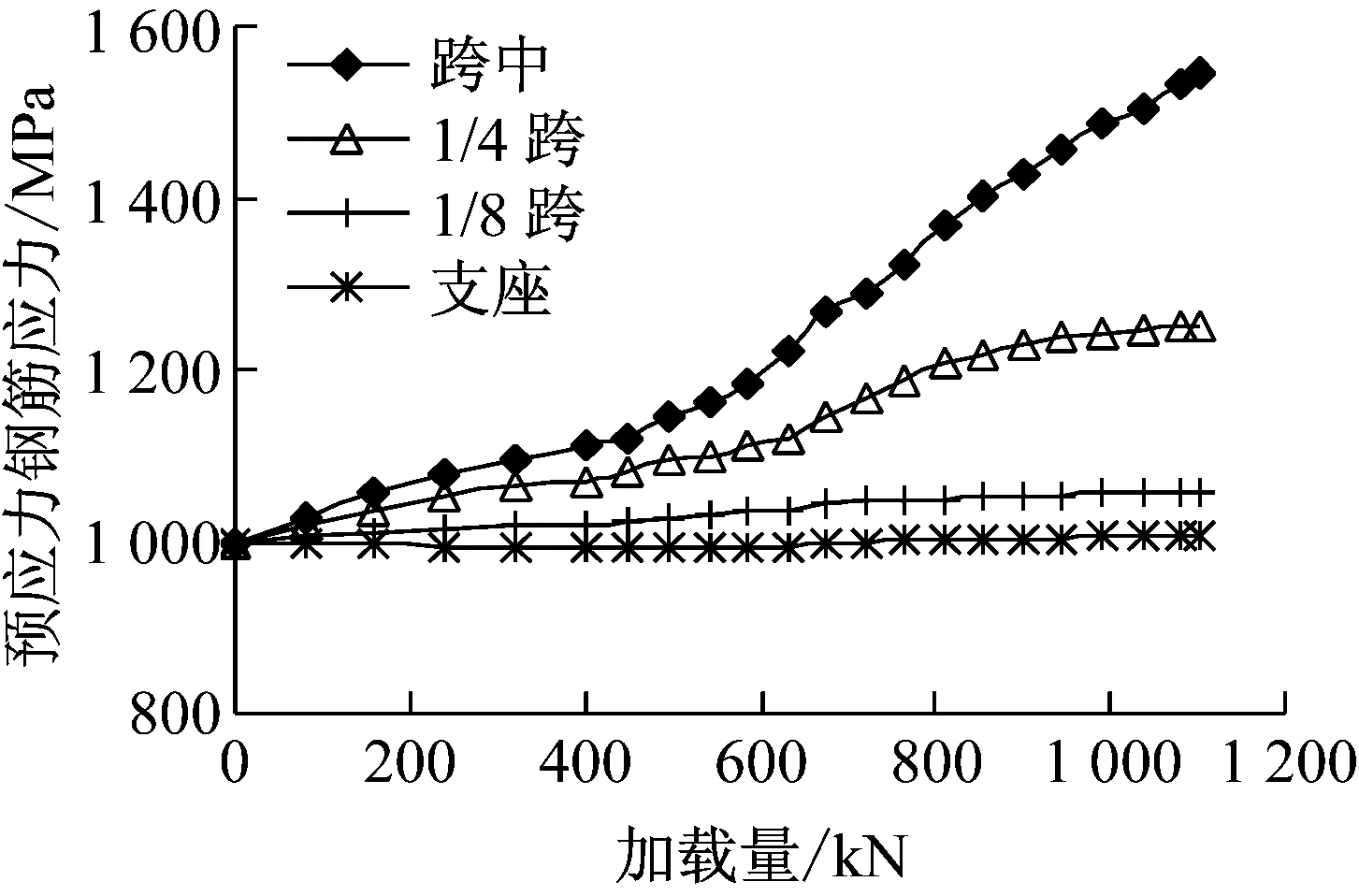
图8 梁底预应力筋的应力荷载曲线Fig.8 Stressload curve of the prestressed tendons at the bottom of the beam

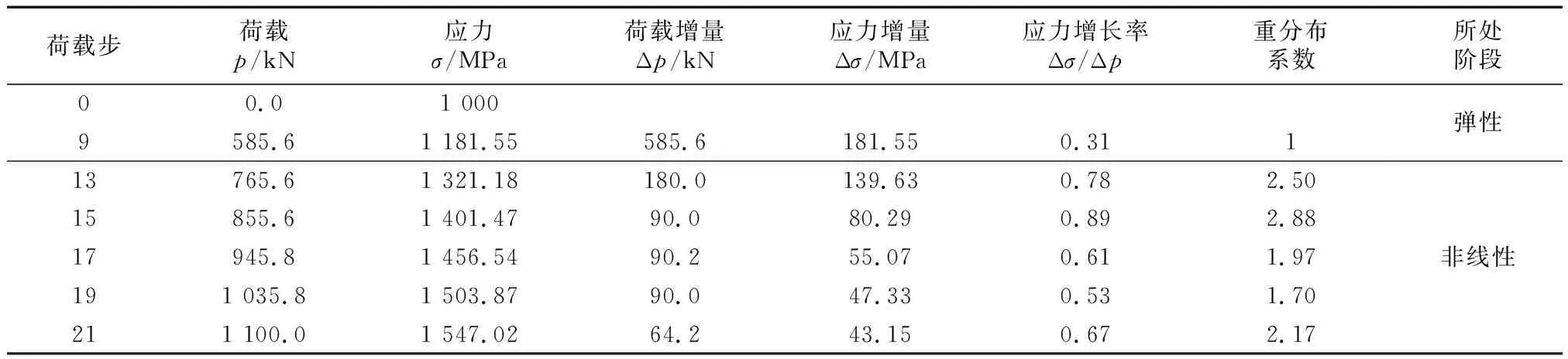
荷载步荷载p/kN应力σ/MPa荷载增量Δp/kN应力增量Δσ/MPa应力增长率Δσ/Δp重分布系数所处阶段00.01 0009585.61 181.55585.6181.550.31113765.61 321.18180.0139.630.782.5015855.61 401.4790.080.290.892.8817945.81 456.5490.255.070.611.97191 035.81 503.8790.047.330.531.70211 100.01 547.0264.243.150.672.17弹性非线性

表2中，90.20=945.8-855.6；55.07=1 456.54-1 401.47；0.61=55.07/90.2；1.97=0.61/0.31.由表2可知，随着荷载增大，预应力筋的应力增长率和重分布系数都发生一定变化，其比弹性阶段相比都有增大.在加载过程中混凝土出现裂缝及压碎后，所施加的荷载逐渐转为由预应力钢筋来承担，故与弹性阶段相比，其应力增长速度较大.

5 结语

本文基于分层壳单元和梁单元计算模式，对预应力钢筋采用壳梁组合单元模拟，对普通钢筋和混凝土采用分层壳单元模拟，推导了壳梁组合单元并对预应力混凝土T梁的受力性能进行了分析.结合试验梁数据分析表明：本文推演的非线性壳梁组合单元用于此类结构分析是合适的，且所采用的Owen准则等能较为有效地描述混凝土T梁的材料非线性；预应力筋的空间预应力效应可采用空间梁单元进行较为准确地模拟；随着加载量增大，预应力混凝土T梁刚度折减系数增大，预应力钢筋的应力增长率较弹性阶段增大，直至结构失效破坏.