基于最小模MUSIC算法的电力谐波/间谐波检测方法
卢洪瑞,郑 威,许劲峰
(江苏科技大学 电子信息学院,镇江 212003)
近些年广泛使用的电力电子设备导致电网中出现大量整数倍基波频率的谐波和非整数倍基波频率的间谐波[1].谐波[2]、间谐波的存在容易引发火灾,降低配电系统的安全等级,变压器正常工作受严重影响等一系列危害[3],准确检测谐波/间谐波是保护用电系统的关键.
目前检测谐波的方法主要有傅里叶变换、加窗插值快速傅立叶变换(fast Fourier transformation,FFT)[4-6]等一些非参数化方法,这类方法计算简单,实时性好,但易受频谱泄漏和栅栏效应影响,分析结果误差较大.虽然采用加窗插值可以减小误差,但是不能摆脱泄漏和栅栏效应影响.多信号分类法(multiple signal dassification,MUSIC)[7-8]、普罗尼(Prony)[9-10]算法、Burg谱估计[11]和旋转不变子空间法(estimationg signal parameters viarotational invariance techniqwes,ESPRIT)[12-13]等现代信号处理的典型方法也被应用到其中,但各有优缺点.以自回归(auto regressive,AR)模型为基础的Burg谱估计法对数据窗外的数据进行线性预测,可以提高频率分辨率,但分析误差受噪声和AR[14]模型阶数影响.MUSIC 和ESPRIT法是基于协方差矩阵的子空间类算法,对信号的频率分辨率较高.
针对谐波检测时传统的傅里叶变换分析精度不高和经典MUSIC算法易受噪声影响等问题,采用最小模(miuimum modulus,MNM)-MUSIC算法进行谐波/间谐波估计.首先用最小描述长度(minimum description length,MDL)准则根据特征值对信号源数目进行估计,然后用加权矩阵对MUSIC算法做出修正,即最小模算法在小特征值对应的噪声子空间的线性组合后与导向矢量的关系估计出各信号的频率,最后用扩展Prony方法得到各信号幅值和相位信息,并通过仿真验证了该方法的精确性.
1 谐波检测原理
1.1 算法流程图
基于MNM-MUSIC算法的谐波/间谐波检测主要流程如图1.
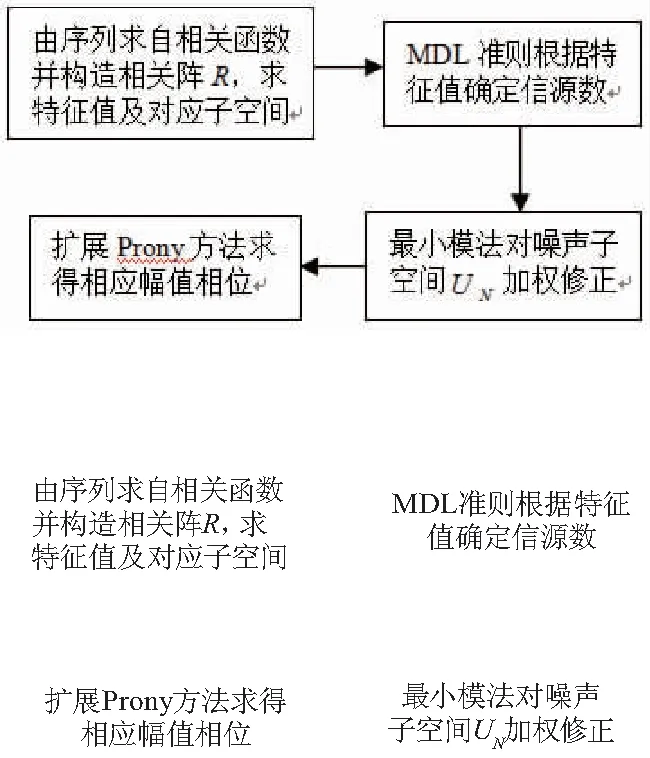
图1 算法流程Fig.1 Algorithm flow
1.2 自相关函数及自相关矩阵的构建
利用MNM-MUSIC方法对信号频率和扩展Prony方法对信号幅值和相位分析时关键问题是准确检测信号源个数,信号源数目的不准确易造成信号子空间和噪声子空间[15-16]不完全正交,曲线中的空间谱峰个数将和真实源数不相同,导致严重误差,此现象为估计信号时的虚警或漏警.
设采样电压(电流)信号的离散时间函数:
(1)
式中:x(n)为采样信号;bi为第i次谐波的幅值;zi=exp(j2πfiΔt),fi为第i次谐波频率,Δt为采样时间间隔;v(n)为白噪声;M为谐波次数;N为采样点数.
将得到的采样序列生成自相关数据rx(m),即自相关函数表示为:
(2)
由(p+1)个rx(m)组成的自相关矩阵R及信号向量分别为:
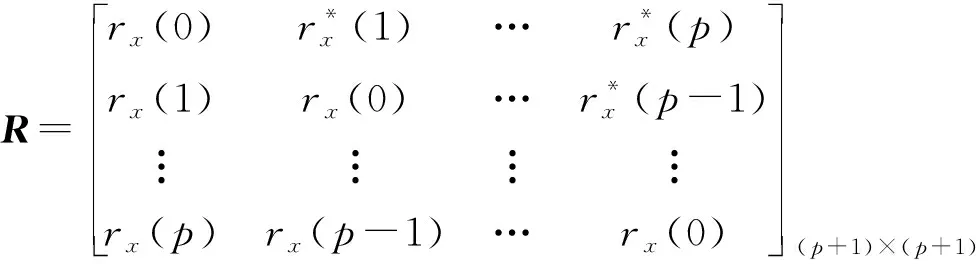
(3)
(4)
其中ωi=2πfi,对式(3)进行特征分解,求得相关矩阵R的特征值.
1.3 信号源数估计
基于信息论方法的一般形式为J(k)=L(k)+p(k),对数似然函数L(k)和罚函数p(k)不同选择对应不同的准则,相应地MDL准则为:
(5)
式中:C为信号特征值的个数,M为待估计的信号源数,H(M)为似然函数,其分母、分子分别为:
(6)
(7)
似然函数H(M)可表示为:
(8)
式中:λi为第i个特征值,将式(8)代入式(5)即得估计信号源数M.
MUSIC算法的应用首先要确定信号子空间的维数,维数过大会产生虚假谱峰,维数过小则会漏掉信号分量.理论上可以通过重复最小特征值的个数来确定噪声子空间的维数,但实际中的最小特征值是有限长数据通过自相关矩阵估计出的,其不可能完全相等.信息论的MDL准则可以在白噪声背景下估计信号维数,其利用最小的MDL(M)所对应的M作为信号子空间维数的估计,盖氏圆盘原理在有色噪声背景下更为适用.
1.4 MNM-MUSIC估计信号频率
1.4.1 经典MUSIC算法基本原理
文中采用均值为零、方差为ρw且相互独立的白噪声.据式(3、4),由自相关矩阵定义知:
(9)
式中:I为(p+1)×(p+1)单位阵,Ai为第i个信号的功率;信号阵Sp的秩最大为M,当p>M时,Sp是奇异阵,但是由于噪声的存在,R的秩仍为(p+1).将信号阵Sp特征分解,即
(10)
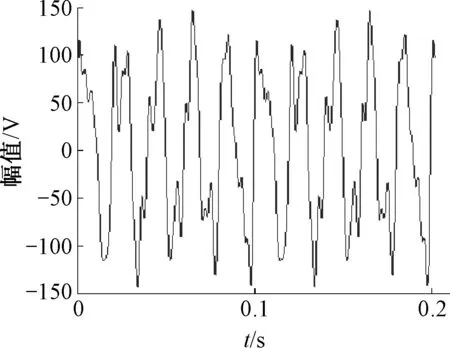
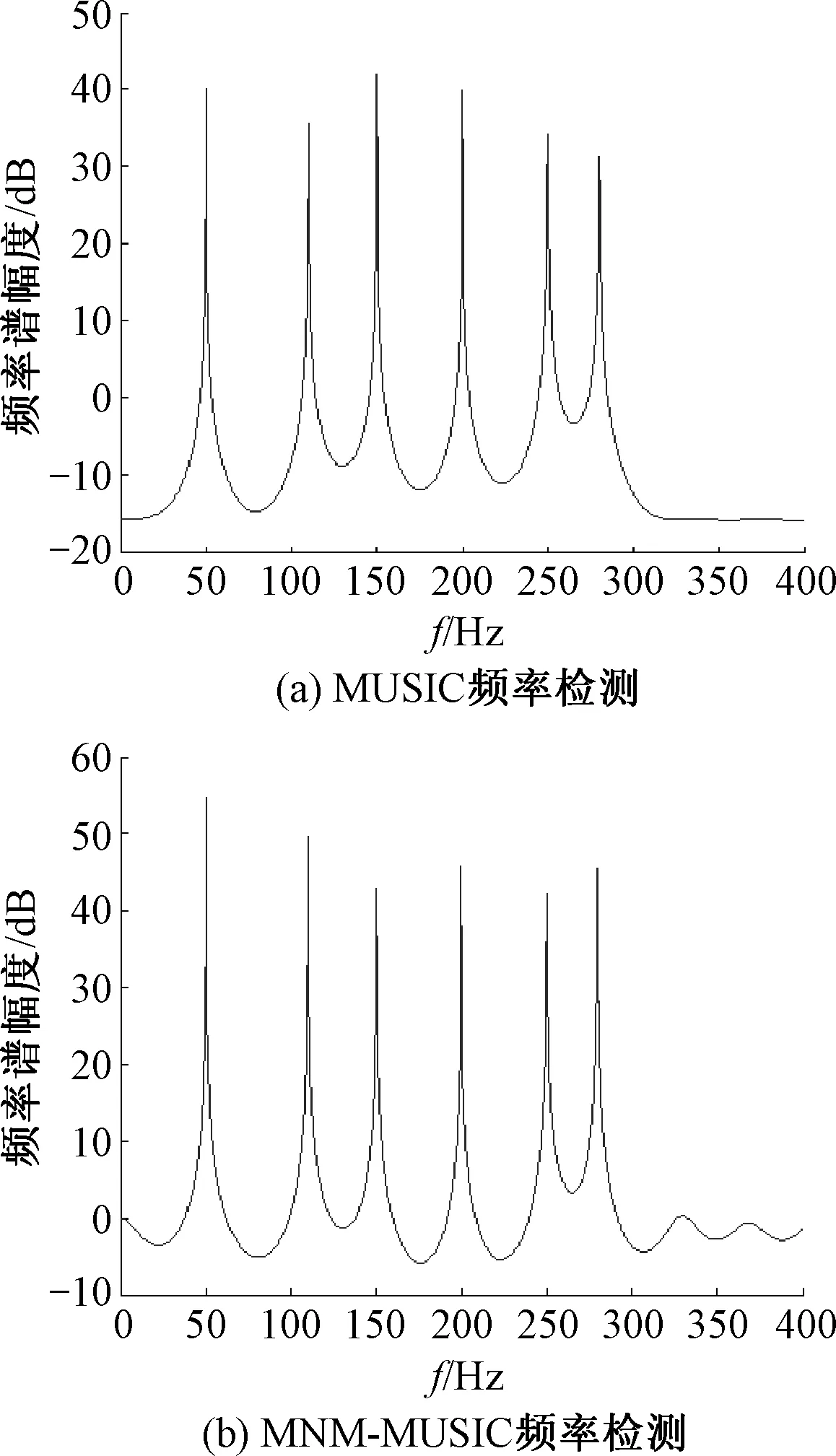
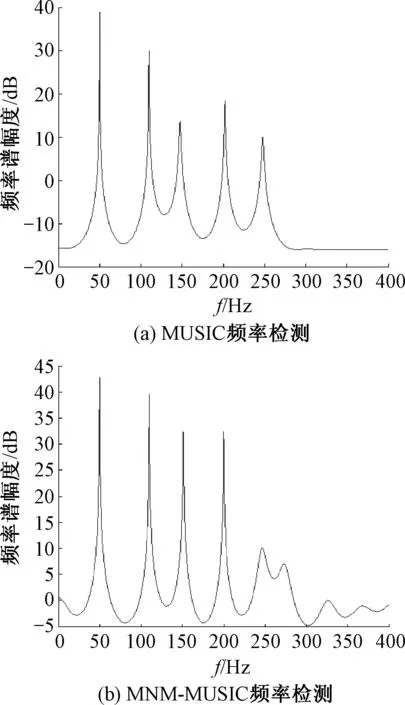
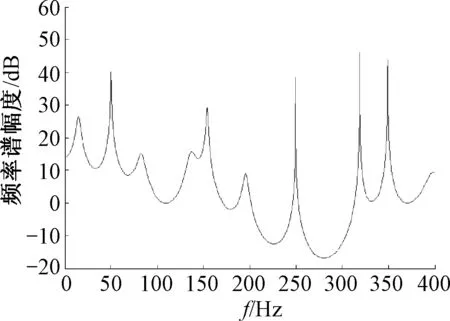
式中:Vi为对应于特征值λi的特征向量,且特征向量相互正交.当rankSp=M (11) 于是,相关阵R的特征分解可表示为 (12) 由此可见,相关阵R和信号阵Sp都有相同的特征向量V1,…,Vp+1,由它们构成一个p+1维的向量空间,且V1,…,Vp+1间彼此相互正交.进一步,将该向量空间分为两个子空间,一个是小特征值都是ρw对应的特征向量VM+1,…,Vp+1构成的噪声子空间;另一个是大特征值(ρw+λ1),(ρw+λ2),…,(ρw+λM)对应的主特征向量V1,…,VM构成的信号子空间.显然,噪声子空间的向量VM+1,…,Vp+1与信号向量ei也是正交的,即VM+1,…,Vp+1的线性组合与信号向量ei正交,得 (13) 令e(ω)=[1,exp(jωi),…,exp(jωip)]Τ,则e(ωi)=ei,由式(13)有 (14) 式(14)中令αk=1,当ω=ωi处为零,基于此,MUSIC算法正是以最小优化搜索实现功率谱分析,即经典MUSIC算法的谱估计可表示为: 在这种供电方式下,信号源支持交流输入,通过小容量UPS为信号源供电。 在市电停电情况下,UPS所带蓄电池为信号源供电。如图2所示。 (15) 1.4.2MNM-MUSIC算法基本原理 由采样序列通过式(2)得到的自相关数据个数p+1,p通常越大检测结果越精确,但p的增大会使计算量大大增加,复杂度的大幅提高不利于硬件实现,给实际应用带来困难,减小p能降低复杂度,但又使估计误差增加,不利于正确分析电力系统谐波/间谐波信号参数,故直接应用经典MUSIC算法检测信号分量带有一定局限性. 经典MUSIC算法中频率的搜索可据式(16)实现,即信号子空间的信号矢量ei与噪声子空间的特征向量VM+1,…,Vp+1并不完全正交,其乘积是一个较小的数,表现为: (16) 但经过式(16)变换方法检测到的高频信号分量处容易产生谱峰分裂和谱峰偏移现象,造成估计误差较大,为了有效避免这种现象,故对式(16)做如下修正: (17) min[eΗ(ω)h′h′Ηe(ω)] (18) 式中:m为噪声子空间的第一行,EN是指噪声子空间除m行外的其余p行. (19) 将h替换式(18)的h′就是所要求的最小模估计值,得到MNM-MUSIC方法检测信号的功率谱分析曲线. (20) 式(20)中在ω=ωi处PMNM(ω)理论值应是无穷大,但由于实际采样数据为有限长和噪声影响使得估计的相关阵和特征值都有误差,即信号子空间的信号矢量ei与特征向量VM+1,…,Vp+1并不完全正交,故在ω=ωi处PMNM(ω)为有限值,但在此处呈现尖峰,在其它点处表现为平缓形态,该峰值对应的频率即是正弦信号的频率. 经修正的MNM-MUSIC方法在低信噪比时的估计偏差小于经典MUSIC方法,当自相关矩阵维数相同时,对谐波检测信号具有更强的适应性,其频谱分析效果优于经典MUSIC方法. 式(1)的矩阵形式表示如下: Zb=x (21) 式中: (22) 范德蒙矩阵Z各列两两相互独立,即为满列秩矩阵,其中zi(i=1,…,p)为利用最小二乘法构造的特征多项式1+a1z-1+…apz-p=0的根,系数a0=0,a1,a2,…,ap由x(n)构造的矩阵X确定. (23) b=(ZHZ)-1ZHx (24) 文中仿真实验所用谐波、间谐波信号为: s(t)=100sin(2π×50t)+40sin(2π×110t+π/9)+20sin(2π×150t+π/7)+16sin(2π×200t+π/6)+13sin(2π×250t+π/5)+10sin(2π×280t+π/3)+v(t) 仿真信号由基波,3、4、5次谐波和间谐波组成,其中间谐波频率幅值分别为110 Hz、40 V,280 Hz、10 V.实际电力系统中存在多种噪声,其中最典型的为高斯白噪声,为模拟实际和验证该方法的抗噪性,故在仿真信号中加入白噪声v(t).实验中,采样频率1 600 Hz,采样点数1 600,仿真信号0~0.2 s的波形如图2. 图2 仿真信号波形Fig.2 Waveform of the simulation signal 信号源数由信息论MDL准则得出,针对同一仿真信号,当自相关矩阵的维数相同(p=40),信噪比不同时,经典MUSIC算法和MNM-MUSIC算法对信号的估计频谱可见图3、4. 图3 SNR=-20 dB时频率检测比较Fig.3 SNR=-20 dB frequencies estimated compared 由图可见,经典MUSIC算法和MNM-MUSIC算法在信噪比SNR=-20 dB时各信号分量频率都能检测,且估计精度较高.如果进一步增大噪声会对经典MUSIC算法造成较大影响,当SNR=-33 dB时,由其 图4 SNR=-33 dB时频率检测比较Fig.4 SNR=-33 dB frequencies estimated compared 估计的结果产生严重误差,导致高频信号分量未能检测;而MNM-MUSIC算法受噪声影响较小,此时各信号分量频率都能准确检测得到.因此,当信噪比更小时MNM-MUSIC算法对信号仍具有较高的频率分辨力,说明文中所提算法具有更好的抗噪性能.信号源数和各信号频率信息都确定后再由扩展Prony方法对信号幅值和相位进行检测. 为了更清晰体现文中方法检测谐波的整体效果,检测效果的评价指标可采用总体相对有效度来描述,其定义形式如下: (25) 式中:m为谐波个数,H(i)为仿真信号频率或幅值的理论值,H′(i)是对估计到的信号频率或者幅度再取平均值. 加窗FFT是离散傅里叶变换的改进算法,理论上对无限长序列的频率变换可实现高频率分辨力,计算简单,实时性好.经典MUSIC直接利用信号子空间的信号矢量和噪声子空间特征向量的正交性构造最小搜索频率范围,优点是不受泄漏和栅栏效应影响,分辨能力强.文中对图2仿真信号分别用3种方法进行实验分析,在信噪比SNR=10 dB、相关阵维数p=40时得出数据参数估计值及其总体相对有效度对比表,如表1. 表1 加窗FFT算法和经典MUSIC算法及文中算法参数估计对比表Table 1 Comparison between the algorithm both window FFT algorithm and MUSIC algorithm 由表1得出,直接用经典MUSIC方法检测信号频率总体相对有效度和加窗FFT方法相差不大,3种方法总体有效度值都接近70,与理论值相比MNM-MUSIC算法估计到的各信号频率更加精确,当信噪比较低时经典MUSIC方法在高频处易产生较大偏差.加窗FFT由于受频谱泄漏影响导致信号能量向附近扩散,表现为检测幅值小于理论值,造成幅值误差偏大;在频率估计方面,由于泄漏的频谱有可能淹没旁边幅度较小的待检信号,导致不能有效估计真实信号源.由表1可看出,基于MNM-MUSIC算法的谐波检测在频率方面的估计效果比以上两种方法更准确,Prony方法的加入使文中算法在幅值和相位估计方面具有更明显优势,其幅值和相位的总体相对有效值分别为24.69、23.72.当相关阵阶数不变而降低信噪比时,仍具有较高的精确度,该方法具有较强的抗噪性.通过仿真实验验证了该算法可以作为电力系统谐波/间谐波分析检测的依据. 从南瑞电气有限公司获得电网中实际的电压数据,利用文中MNM-MUSIC算法对实际采样数据进行频率分析.图5为实时信号波形图,采样频率为1 600 Hz,图6为利用该方法分析得到的实时信号频率特性图,由图可见,该电压信号含有大量谐波和间谐波. 利用文中MNM-MUSIC算法可以将电压中含有的基波和各次谐波/间谐波信号提取出来.由图6可见,电力系统中的3、5、7次谐波成分较明显,其危害较大. 图5 实时信号波形图Fig.5 Waveform of real-time signal 图6 频率检测结果Fig.6 Frequencies estimated results 检测到的谐波和间谐波频率分别为50.5,152.8,249.6,350.9 Hz;20.3,78.1,139.3,192.6,320.7 Hz.通过实际的检测结果与分析表明该方法可以应用在实时数据处理分析中,并具有较高的准确性. 文中算法采用信息论准则中的MDL准则,在典型白噪声背景下利用自相关矩阵R的特征值信息估计信源数.由此可确定较小的k=M+1,…,p+1个特征值对应的噪声子空间VM+1,…,Vp+1,分别对噪声空间取第1行和第2到p+1行并做加权归一化处理得到最小模估计器h,即得到MNM-MUSIC方法估计到的各信号分量频率信息.基波、谐波和间谐波的频率确定后,再应用扩展Prony方法估计其幅值和相位,从而精确地检测到电力信号分量的各项参数. 仿真实验证明该算法比其它两种方法的频率、幅值和相位估计精度都高,总体相对有效度描述了3种方法在准确性方面的数据对比变化情况.与经典MUSIC算法相比,文中算法抗噪性强,在相关阵阶数相同时更加精确地估计各信号分量参数信息,使分析评判参数更有价值,有利于实际应用.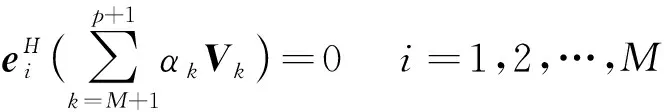
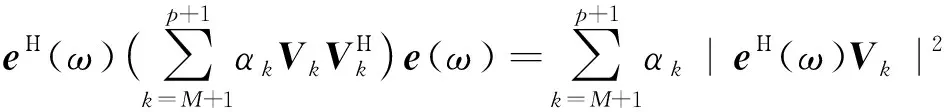
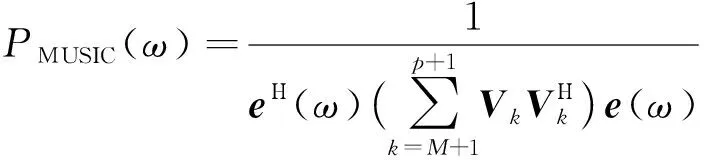


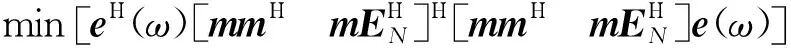
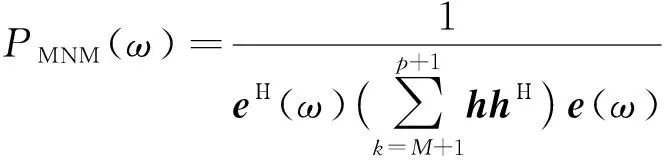
1.5 扩展Prony方法检测信号幅值和相位
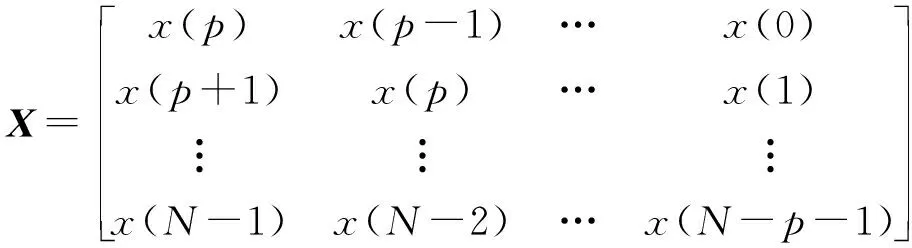
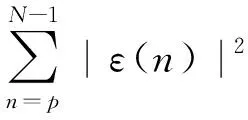
2 仿真实验与结果分析

3 实际数据检测与结果分析

4 结论

