水面无人艇航向的新型变结构全局快速终端滑模控制方法
张 晨,薛文涛,侯小燕
(江苏科技大学 电子信息学院, 镇江 212003)
水面无人艇,一种无人操作的水面舰艇,常用于执行比较危险的不适合有人操作的任务,诸如多种战争和非战争等军事任务.无人艇在水面运行时,由于存在风、浪、流等复杂的环境干扰因素,并且随着航行速度的改变,系统存在较强的不确定性和时变性,不仅精确模型的建立难度较大,无人艇的航向也会不可避免偏离给定轨迹.为了解决无人艇自动碰壁、航迹跟踪偏离等问题,实现其自主航行,精确的航向控制势在必行.
近年来,针对不确定无人艇非线性模型,先进的航向控制技术取得较大进展.现有的较先进的非线性控制方法,如反馈线性化、鲁棒控制、滑模控制、自适应控制、人工智能控制等已应用于水面无人艇航向的控制并取得了一定的成果[1-6].文献[7]针对喷水推进型高速无人艇,采用神经网络作为辨识器,提出一种新的模糊控制策略,设计了模糊PID控制器并经过仿真验证了其有效性.该方法结合神经网络和模糊控制的优点,不需要被控对象的精确模型.文献[8]提出一种模糊自适应PID无人艇航向控制算法,给出自适应模糊参数调节规则,实现了控制器参数的在线调节和无人艇航向的跟踪控制.但以上方法中,模糊理论要根据先验知识,神经网络则要在其复杂度和逼近精度间进行折中.文献[9]将支持向量机引入到水面无人艇的航向控制中,提出一种自适应支持向量机逆控制方法,通过进行逆动态模型和逆误差补偿项的离线辨识得到最终控制器,但该方法要求动态模型可逆且离线辨识较为复杂.文献[10]针对单泵喷水推进型无人滑行艇航向跟踪的非线性系统控制,基于反演方法和滑模控制理论,设计了自适应滑模控制器,该方法通过系统不确定估计提高了系统的鲁棒性,但系统的收敛速度和参数估计精度有待进一步提高.
因为滑模控制具有较强的鲁棒性[11-12],其滑动模态可以自由设计,且与对象参数和扰动无关,但传统滑模由于控制量的不连续切换在实际应用中受限,从而导致系统抖振.一般来说,线性滑模面是构成普通滑模控制的一种主滑模面,系统轨迹在线性滑模面的作用下到达滑动模态之后,系统状态不但逐渐收敛于零,且可以利用滑模面参数矩阵的选择来调节收敛的速度.传统的终端滑模控制方法同样由非线性滑模面来设计,在有限时间内,虽然可以使系统的状态收敛到零,并且系统的动态性能好于传统的线性滑模控制,但是在系统离平衡点较远时,普通的终端滑模控制的收敛速度要低于线性滑动模态.为此,文中采用一种新型变结构全局快速终端滑模控制[13-15],全局快速滑模控制在滑动模态的设计综合了Terminal滑模控制和传统滑模控制的优点,同时在到达阶段运用快速到达的概念,使得系统状态无论在远离平衡点的时候,还是接近平衡点时都具有一定的快速收敛速度.
1 无人艇航向系统模型
水面无人艇的实际运行模型如图1,考虑操舵不是很频繁的条件下,当系统存在外部环境扰动等不确定因素时,可用如下一阶非线性艏摇响应方程来描述船舶航向非线性操作系统:
(1)
式中:ψ为无人艇艏向角(顺时针为正),r为无人艇艏摇角速度,T为时间常数,K为回转性指数,δ为控制舵角(右舵为正),α为模型非线性项系数,d为未知外部扰动的不确定性影响.

图1 水面无人艇Fig.1 Unmanned surface vehicle
考虑喷水推进型水面无人艇,与文献[16]中所采用的模型一致,因此文中舵角δ为喷水推进器喷嘴的转角,通过改变喷嘴角和喷水量来控制水面无人艇的航行方向和航行速度.
在实际应用中,无人艇模型中的参数K,T,α较难获取,且当无人艇的航行速度改变时,系统模型参数也会随之改变.因此水面无人艇航向控制问题的实质在于:在存在系统不确定和外部扰动情况下,设计合适的自适应控制律,从而使水面无人艇航向精确跟踪给定轨迹.
2 变结构全局快速终端滑模控制方法
普通终端滑模的形式为:
(2)
式中:x1∈R1为常数;p>q,且为奇数.对于给定初始状态x1(0)≠0,系统将在有限时间ts1内到达x1=0,ts1由下式决定:
(3)
全局快速终端滑模的形式为:
(4)
式中:λ、β>0,且p>q为奇数.由式(4)得:
(5)
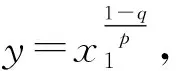
(6)
其通解为:
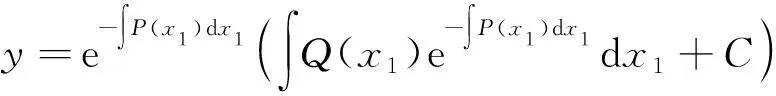
(7)
则式(7)的解为:
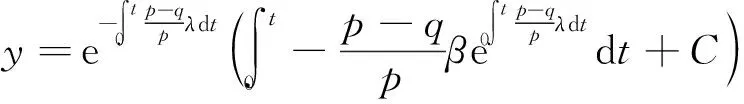
(8)
t=0时,C=y(0),上式变为:
(9)
由于x1=0时,y=0,t=ts1,上式变为:
(10)
在滑动模态上从任意初始状态x1(0)≠0收敛到平衡状态x1=0的时间为:
通过λ、β、p、q的设定,在有限时间ts1内,系统可以趋近平衡状态.再根据式(4),有

3 水面无人艇航向变结构全局快速终端滑模控制器设计
一种具有递归结构的快速滑动模态表示为:
(11)
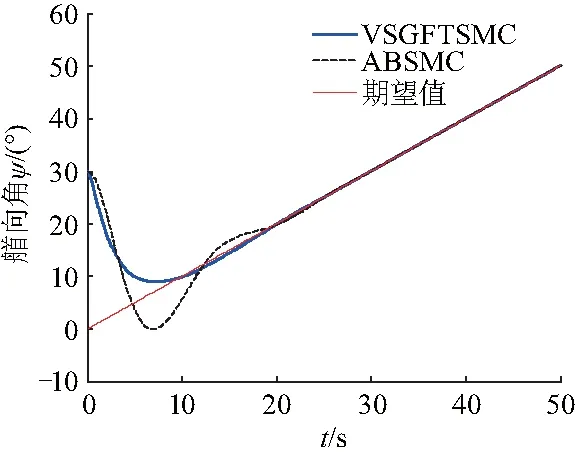
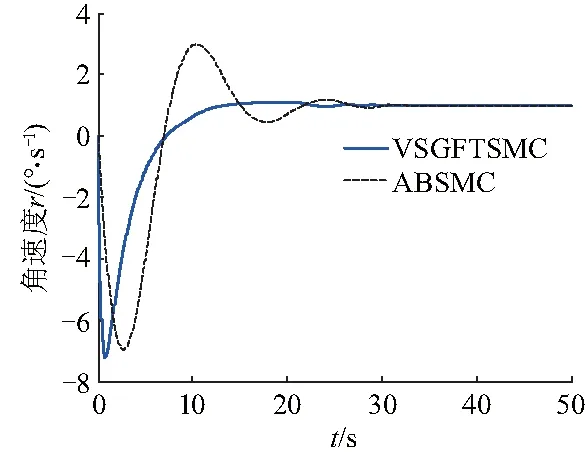
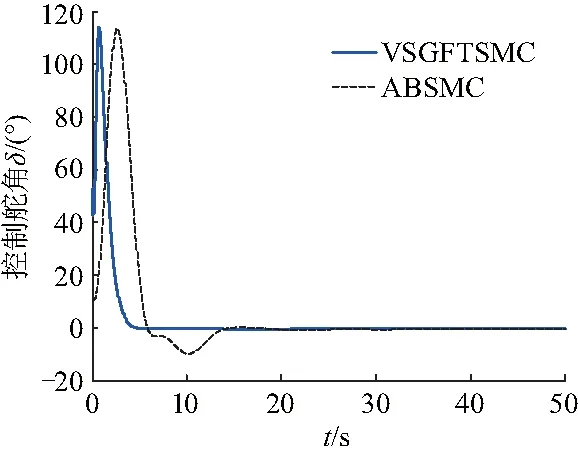
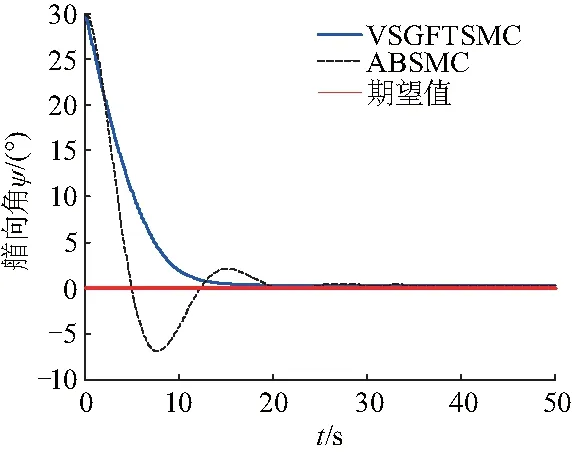
式中:λi、βi>0,且qi、pi(qi (12) 式中:s0=x1. 由式(12),系统状态沿 (13) 式中:φ、γ>0,p、q(q 定义Lyapunov函数: (14) (15) 设x1=ψ,x2=r,u=δ.则系统(1)为: (16) 则由式(12)得全局快速滑动模态控制律为: (17) 当建模不确定性和干扰较大时,需要切换项增益η较大,这就会造成较大的抖振.为了防止抖振,控制器中采用饱和函数sat(s)代替符号函数sgn(s),即 (18) 式中:Δ为边界层,且为较小的正常数.在理想滑动模态的某一Δ邻域内,系统的运动轨迹可以完全被限制在区域内,因此,可称为准滑模控制,此Δ邻域为滑动模态切换面的边界层.在边界层内,它不需要满足滑动模态时的存在条件,因此也不要求在切换面上进行控制结构的切换,而是在Δ边界层上进行结构变换,这种差别从根本上避免或削弱了抖振,在实际中得到广泛应用. 为验证所设计控制器的有效性,采用MATLAB仿真软件进行实验分析.对给出的非线性系统(1)在控制律式(17)的作用下进行仿真,并将结果与文献[19]所用方法及基本的反演滑模控制在相同初始条件下的仿真结果进行比较. 根据海试操纵性试验的结果,可选取如下模型参数:K=-2.364,T=5.489,α=0.94.给定系统初始条件:ψ0=30°,r0=0,设置期望的航向为斜坡函数ψd(t)=t和直航ψd=0.外部扰动d=cos πt.文献[10]采用自适应反演滑模控制( adaptive backstepping sliding mode control,ABSMC)方法,其控制器参数取值:c1=0.7,c2=0.3,k1=0.5,h=0.15,β=γ=0.001.文中采用新型变结构全局快速终端滑模控制方法(variable structure global fast terminal sliding mode control,VSGFTSMC),设计的控制器参数取值:λ0=2,β0=1,P0=9,q0=5,φ=10,γ=10,p=3,q=1,η=0.1,D=1(d=cos πt≤1). 图2~7为两种控制方法下水面无人艇航向控制的仿真对比.其中,图2~4分别是航向设定值为斜坡函数时的艏向角ψ,角速度r和控制舵角δ的响应曲线.图5~7分别是航向设定值为直航ψd=0时的艏向角ψ,角速度r和控制舵角δ的响应曲线. 由仿真结果可以看出,尽管存在不确定外部扰动,VSGFTSMC及ABSMC两种方法均能实现无人艇航向的准确跟踪控制. 由图2、5可以看出,在不确定扰动影响下,不同初始值情况下VSGFTSMC方法控制的艏向角进入稳态的时间都为t=16 s左右,而ABSMC则需要18 s左右,说明跟踪速度更快,输出也平稳,波动更小,航向输出光滑.由图3、6可知,VSGFTSMC方法控制的角速度到达稳定所需要的时间都为t=15 s左右,而ABSMC则分别需要需t=28 s、t=25 s,说明前者方法控制下的角速度过渡时间短,收敛过程平稳且快速.由图4、7可知,与ABSMC方法的控制律相比,VSGFTSMC方法的控制律在t=5 s、t=6 s的时候进入稳态,而ABSMC则所需要的时间为t=12 s、t=14 s,前者收敛时间更短,而且很明显从图中可以看出前者方法的控制舵角波动更小.所以VSGFTSMC方法具有较好的动态跟踪性能和自适应能力. 综合两种情况下实验分析,VSGFTSMC和ABSNC两种控制策略都能有效控制无人艇航向运行在期望的状态,但是文中提出的方法在收敛时间上明显更短,动静态性能更好. 图2 ψd(t)=t时,艏向角ψ响应曲线(ψ0=30°)Fig.2 Response graph of yaw ψ(ψ0=30°),when ψd(t)=t 图3 ψd(t)=t时,角速度r响应曲线Fig.3 Response graph of angular velocity r,when ψd(t)=t 图4 ψd(t)=t时,控制舵角δ响应曲线Fig.4 Response graph of control rudder δ,when ψd(t)=t 图5 ψd(t)=0时,艏向角ψ响应曲线(ψ0=30°)Fig.5 Response graph of yaw ψ(ψ0=30°),when ψd(t)=0 图6 ψd(t)=0时,角速度r响应曲线Fig.6 Response graph of angular velocity r,when ψd(t)=0 图7 ψd(t)=0时,控制舵角δ响应曲线Fig.7 Response graph of control rudder δ,when ψd(t)=0 针对外部扰动不确定无人艇航向非线性系统,采用的新型变结构全局快速终端滑模控制方法应用于无人艇的航向控制.仿真结果得到如下结论: (1) 基于新型变结构全局快速终端滑模的控制器的控制效果良好,对外界干扰也具有很强的抑制能力,使被控系统在整个控制阶段都具有较强的鲁棒性. (2) 无人艇航向的跟踪性和稳定性得到提高.同时设计的连续滑模控制律也消除了滑模控制的抖振,加快了系统状态的收敛. (3) 所采用的新型变结构全局快速终端滑模控制方法与文献[10]所运用的多算法结合控制相比较,控制效果更好.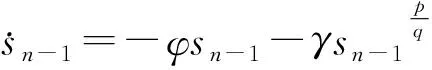
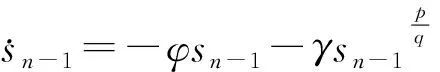
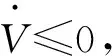


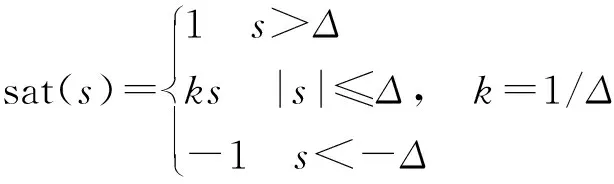
4 仿真实验分析


5 结论

