水下浮动锚索—平台结构耦合非线性参数振动研究

苏 波,张序彦,于国军

(江苏大学 土木工程与力学学院, 镇江 212013)

2005年,美国密歇根大学的Bernitsas教授提出了潮流能发电系统VIVACE(vortex induced vibration aquatic clean energy)[1-3],并在实验室进行模型试验(图1)．这是一种新型的潮流能发电系统,其基本原理是将圆柱体由水流涡激振动产生的机械能转化为电能，与传统水轮发电机相比，它能够有效避免发电装置对于鱼类的伤害,降低对海洋生态的破坏．随后,Bernitsas教授团队分别在圣克莱尔河的休伦港、荷兰的于尔夫特、新泽西的里昂纳多等地做了一系列的现场试验[4-5]．

该装置设计为安装在河流或海洋底部,由于支架高度的限制,圆柱不可避免受流动速度变化梯度的影响．为更有效地捕捉稳定洋流,同时适用远海、深海等复杂海洋环境,改进为悬浮式潮流能发电系统F-VIVACE(floating vortex induced vibration aquatic clean energy),如图2．该系统主要由锚碇、锚索(选用钢缆锚索)、平台发电装置组成,中空平台提供浮力使发电装置悬浮在合适流速的水域,平台则由锚索锚固于海底．

图1 VIVACE潮流能发电系统Fig.1 VIVACE tidal current energy conversion system

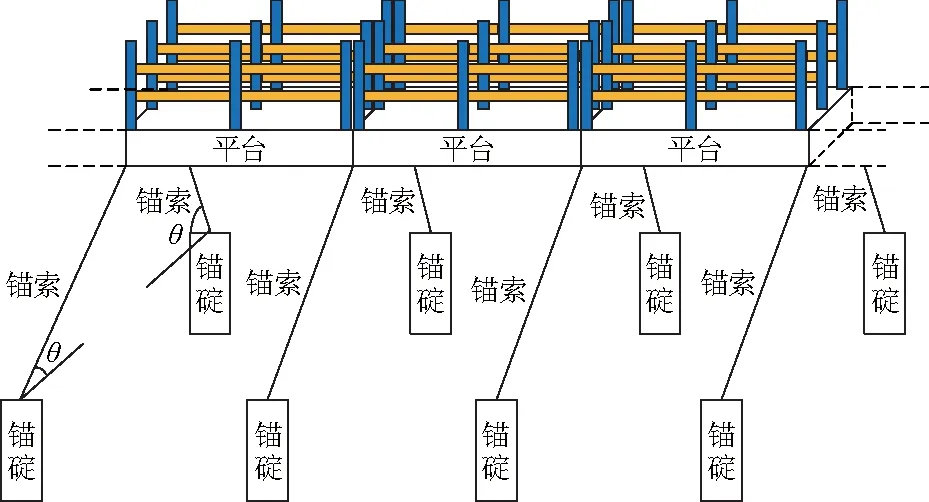
图2 悬浮式VIVACE潮流能发电系统Fig.2 Floating VIVACE tidal current energy conversion system

F-VIVACE系统类似于锚泊系统,锚索为该结构的主要受力部件,其柔度大,质量小,极易发生复杂的动力响应[6]．其中,当该系统在上部结构工作时,由于发电装置的涡激振动以及洋流的作用下平台会发生竖向振动,进而导致锚索发生类似于斜拉桥和悬浮隧道拉索的参数振动[7-8]．即使极小的扰动也会导致锚索的大幅振动[9]．因此有必要对该现象进行分析研究,避免锚索发生大幅非线性振动以保证结构的安全性,适用性．对于锚索参数振动的研究,主要集中于斜拉桥的拉索和悬浮隧道的锚索．主要动力学模型有两类:一类是理想激励源模型,另一类是非理想激励源模型[10]．理性激励源是指忽略锚索对结构作用,只考虑结构对锚索的作用,将锚索端部的激励视为理想的正弦或余弦函数建立振动方程[11-13];非理想激励源则认为锚索对结构的作用不可忽略,将锚索和结构视为一个系统建立耦合振动方程组[14-17]．文中将锚索激励视为非理想激励,考虑锚索对平台的拉力建立锚索—平台耦合振动模型．

第1部分根据F-VIVACE系统的振动特点,建立考虑锚索浮力,垂度及水体影响的耦合振动方程组；第2部分将采用MATLAB,对所建立的耦合振动方程进行程序编制,通过数值计算,分析水体对锚索的作用力、锚索和平台初始扰动的大小、锚索初始张力、锚索和平台阻尼对锚索振动的影响；第3部分将调频质块阻尼器[18](TMD)应用于该系统,并验证其减振效果．

1 锚索—结构耦合参数振动模型

选取一段发电平台作为典型计算单元,并根据结构对称性可将之简化为如图3(a)所示结构,用集中质量块M模拟发电平台,用弹簧K模拟结构刚度,用阻尼器C模拟结构阻尼,建立锚索—平台耦合振动模型．

F-VIVACE系统的主要振动方向为竖直方向,如图3(a)．将其分解为垂直于锚索方向和沿锚索方向,如图3(b)、(c)．其中,如图3(b)所示的振动为强迫振动,如图3(c)所示的振动为参数振动[15-16]．由于参数振动中极小的激励也会引起锚索的大幅振动[8],因此,选取如图3(c)所示参数振动耦合振动模型作为研究对象．

为方便问题的研究,对该模型作基本假定:

(1) 忽略锚索的抗弯刚度、抗剪刚度、抗扭刚度[14];

(2) 考虑锚索的垂度,其初始构型为二次抛物线[16];

(3) 不考虑锚索的材料非线性,张力、材料性质不沿长度方向改变且符合胡克定律;

(4) 引用Morison公式[19-20],以考虑水体对锚索的影响．

取长度为ds的一段锚索作为研究对象,其动平衡状态时受力,如图4．

图4 锚索单元体动力平衡时受力Fig.4 Dynamic force diagram of cable element

由牛顿定律可建立锚索的振动微分方程[21]:

(1)

式中:z为锚索自重作用下静态曲线；w为锚索的动位移；T为锚索的切向拉力；m为单位长度锚索质量；c为锚索的阻尼系数；s为锚索弧长；FD为锚索振动引起水体对其单位长度的作用力；Fw为单位长度锚索所受的重力及浮力．

T由初始张力与动应力组成:

T=T0+EAε

(2)

式中:T0为锚索的初始拉力；EA为锚索的抗拉刚度；ε为锚索的动应变．

FD为振动时水体对锚索的作用力,由于锚索可近似为细长柱体,故其可由Morison公式给出[20],可表示为水阻尼力与附连水惯性力之和:

(3)

式中:ρw为水的密度;d为锚索的直径;CD为拖拽力系数,取0.7;Cm为附加质量系数,取1[17]．

Fw由阿基米德原理可表示为:

Fw=-(m-ρwA)gcosθ

式中:A为锚索横截面积;g为重力加速度;θ为锚索微段与水平方向倾角．

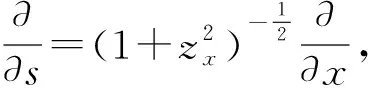
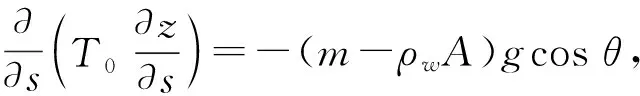
(4)

由基本假定2,锚索初始线型采用二次抛物线[16]:

z=4(h/L)(x-x2/L)

(5)

式中:h为锚索考虑浮力时的跨中垂度,h=(m-ρA)gcosθL2/8H;H为锚索初始平衡时轴向拉力．

H与T0的关系:

则

(6)

锚索的动应变可表示为[15]:

(7)

式中:X为锚索端部位移；εX为锚索端部位移引起的应变；εl为锚索变形引起的应变．

由锚索的初始线型式(5),可得:

zx=4(h/L)(1-2x/L)=4hf/L

zxx=4(h/L)(-2/L)=-8h/L2

(8)

(9)

将式(5～9)代入式(4)可得:

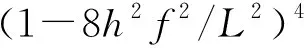
(10)

将式(10)进一步写为:

(1-8h2f2/L2)Hwxx+EA[(16f2h2/L2+X/L-

16Xf2h2/L3)wxx+(32Xh2f/L4-64fh2/L3)wx]+

(11)

由于锚索的垂跨比较小,可取标准弦模态作为锚索的振动模态[22],即:

(12)

由于在锚索的振动中第一阶振型占主导地位[23],因此可以应用伽辽金法,取第一阶振动模态对式(11)进行整理得[17]:

(13)

式中:

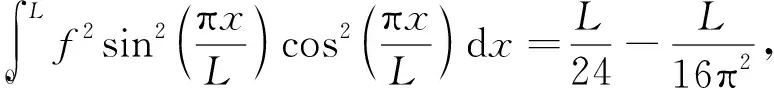
(14)

式(13)可进一步写为:

(15)

式中:

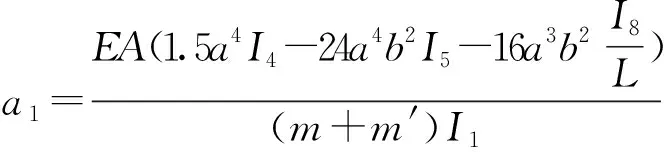
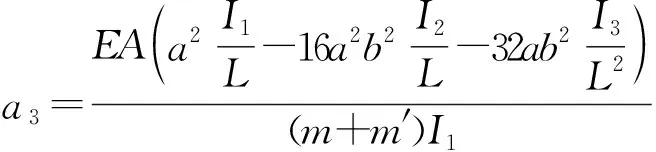
(16)

对于平台的运动,根据牛顿定律:

(17)

式(17)可进一步写为:

(18)

式(15-18)即为锚索—平台耦合振动方程组:

(19)

式(19)可进一步写为:

(20)

式中:

(21)

式中：ω1为锚索自振频率；ω2为平台的自振频率；ξ1为锚索的阻尼比；ξ2为平台的阻尼比．

2 数值算例及结果分析

结合文献[9,15,24]中悬浮隧道的锚索参数，选取锚索—平台基本参数(表1)．采用MATLAB编制程序对该系统进行数值分析,采用四阶-五阶Runge-Kutta算法对该方程组进行数值分析,得到不同工况下的锚索—结构振动的位移时程曲线．分析中假定平台的质量不变,通过调节刚度改变其固有频率使其满足ω1≈0.5ω2．锚索初始扰动Δ1=0.001m,平台初始扰动Δ2=0.1m,初始张力T0=4.9×106N．

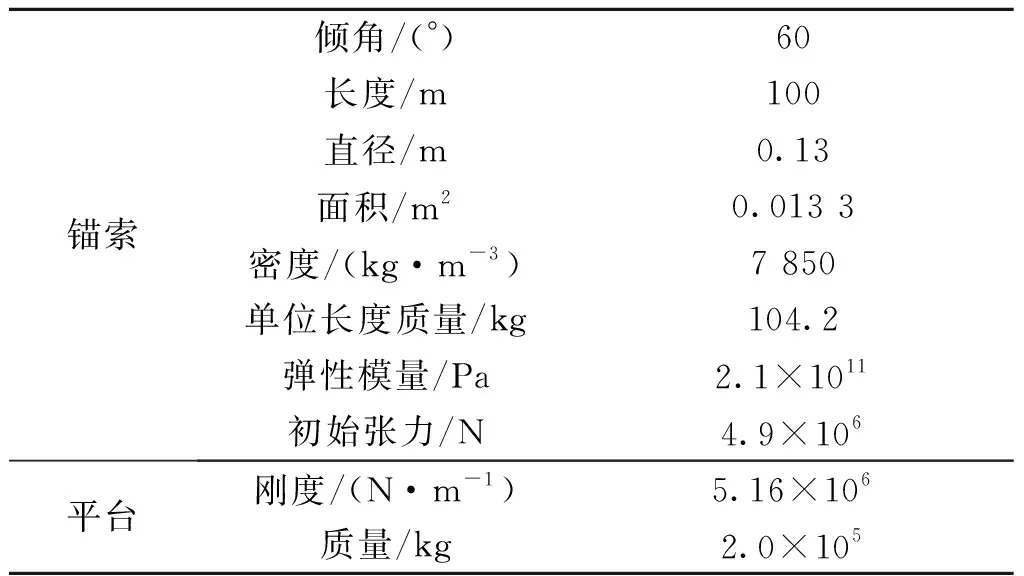
表1 系统基本参数Table 1 Basic parameters of the system

对于锚索—平台耦合参数振动的分析下文将选取具有代表意义的几个工况进行分析,具体工况见表2．

表2 工况列表Table 2 List of working conditions

表中：Δ1为锚索初始扰动；Δ2为平台初始扰动；ξ1为锚索阻尼比；ξ2为平台阻尼比；fD为水阻尼力；fI为附连水惯性力；T0为初始张力．

锚索的自振频率与锚索的长度、单位长度质量及锚索的初始张力有关,由式(16)可得锚索的固有频率ω1为:

代入锚索参数可得ω1为6.46 Hz．

平台的自振频率与平台的质量、刚度有关．由式(21)可得平台的自振频率ω2为:

代入平台参数可得ω2为12.86 Hz．ω1≈0.5ω2,此时将会发生参数振动现象,下文将以此频率关系进行锚索—平台的耦合参数振动研究．

2.1 无水体及阻尼影响时系统响应

图5为工况1下锚索和平台的位移时程曲线;在工况1下,由于不考虑水体影响及系统阻尼,此时式(1)中的c、FD和Fw变为0,式(20)中的第1式与斜拉桥索—桥耦合振动系统中拉索的振动方程[15]类似,变为:

(22)

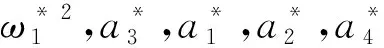
平台振动方程式(20)中的第2式变为:

(23)

将式(22)与式(23)组成方程组,通过数值分析计算得锚索、平台的位移D时程曲线如下图:

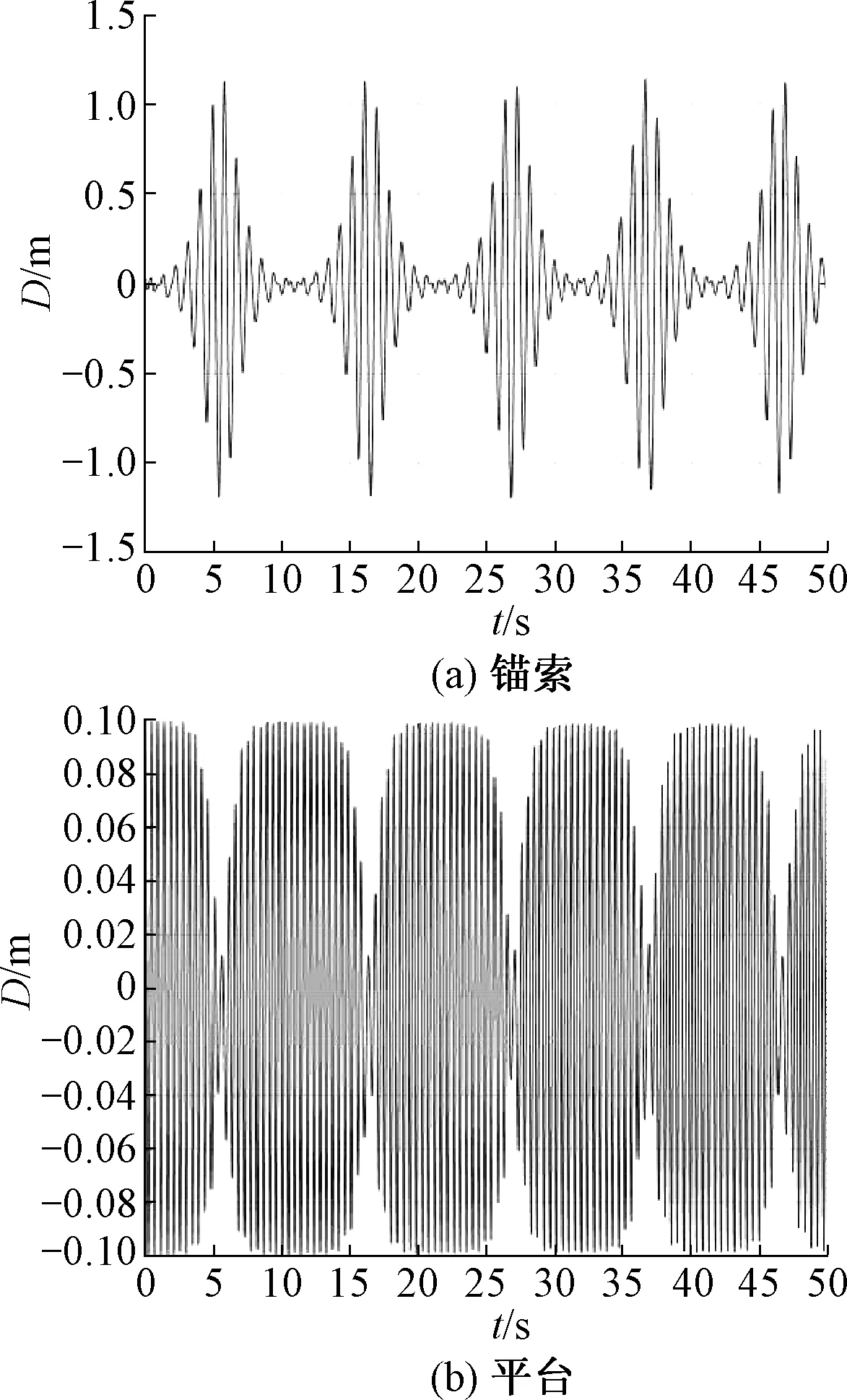
图5 工况1下锚索与平台位移时程曲线Fig.5 Displacement history of cable and platform in working condition 1

从图5(a)中可以看到锚索发生参数共振,其振幅由初始的0.001 m迅速增大到接近1.2 m．同时,锚索和平台的振动呈现出周期性的特点,即“拍”的特征;锚索和平台的振动发生强烈的耦合,锚索的最大振幅处对应着平台的最小振幅,平台的最大振幅对应于锚索的最小振幅,这表明能量在锚索和平台之间相互传递．

2.2 考虑附连水惯性力时系统响应

(24)

平台振动方程,式(20)中的第2式变为:

(25)

将式(24、25)组成方程组,通过数值分析计算得锚索、平台的位移时程曲线如图6.

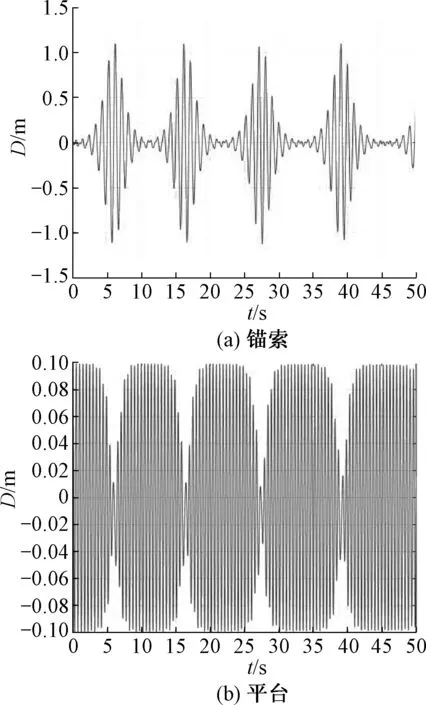
图6 工况2下锚索与平台位移时程曲线Fig.6 Displacement history of cable and platform in working condition 2

从图6(a)中可以看出,相比于图5(a)所示锚索振动“拍”的频率明显变小;同时,锚索的振幅也有所减小,其最大振幅由1.2 m减小到1.1 m．这是由于附连水惯性力在系统中主要体现在锚索的附加质量m′上,由式(16)可以看出随着锚索质量的增大,锚索的振动频率变小,从而导致“拍”频变小．在锚索和平台初始扰动不变即平台传递给锚索能量不变的情况下,锚索质量的增加会导致锚索振幅的减小,这也符合能量守恒定律．由于相对于平台的质量,锚索增加的附加质量m′非常小,所以如图6(b)所示平台的振幅没有出现明显改变．

2.3 考虑附连水惯性力和水阻尼力时系统响应

图7所示为工况3下锚索和平台的位移时程曲线．在工况3下,由于考虑水体影响但忽略系统阻尼的影响,此时式(20)中的第1式变为:

(26)

平台振动方程,式(20)中的第2式变为:

(27)

将式(26)与式(27)组成方程组,通过数值分析计算得锚索、平台的位移时程曲线如图7.

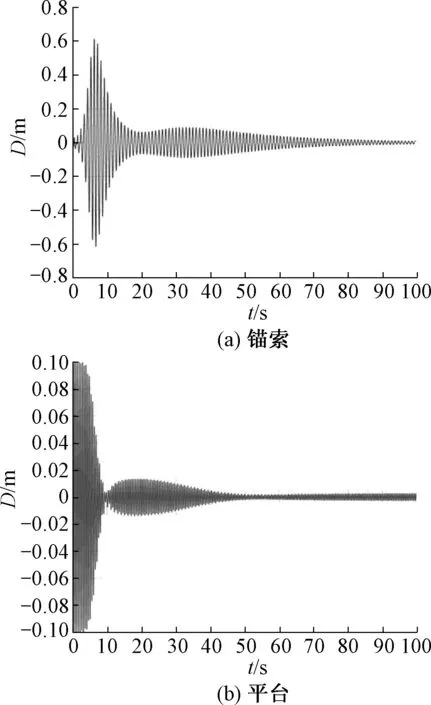
图7 工况3下锚索与平台位移时程曲线Fig.7 Displacement history of cable and platform in working condition 3

从图7(a)中可以看出：当考虑水体阻尼的影响时,锚索的振幅明显减小;最大振幅由1.1 m迅速减小到0.6 m．在图7(b)中,虽然平台的振幅在第1个“拍”内并未有明显减小,但在第2个“拍”后平台的振幅迅速从0.1 m降到0.01 m．在水阻尼力的作用下,锚索和平台的振动会被迅速削弱并随着时间的推移直至消失．

2.4 初始扰动对系统响应的影响

图8、9分别为工况4、5下锚索和平台的位移时程曲线．对式(20)通过数值分析计算得两种不同初始扰动下锚索、平台的位移时程曲线如图8、9.

与工况3相比较,工况4下,锚索的初始扰动由0.001 m增大到0.05 m,增大了50倍,而从图8(a)与图7(a)所示的锚索位移时程曲线中可以看到锚索振幅并未显著增大,仅从 0.617 m增大到 0.619 m,增加了0.32%,几乎可以忽略;平台的振动亦未发生显著变化．

图8 工况4下锚索与平台位移时程曲线Fig.8 Displacement history of cable and platform in working condition 4

图9 工况5下锚索与平台位移时程曲线Fig.9 Displacement history of cable and platform in working condition 5

与工况4相比较,工况5下,平台的初始扰动由0.1 m增大到0.2 m,增大了2倍,从图9(a)与图8(a)所示的锚索位移时程曲线中可以看到锚索振幅明显增大,从0.6 m增大到1.22 m,增加了103.33%;同时从图8(b)所示的平台位移时程曲线中可以看到平台的“拍”的频率有所增大．由此,相对于锚索,平台的初始扰动对锚索的振幅的影响更显著,这可以理解为平台的质量更大,初始扰动给系统提供的能量更多引起的[12]．

2.5 初始张力对系统响应的影响

图10为工况6下锚索和平台的位移时程曲线．此时,式(13)变为：

(28)

由式(28)可知,当锚索的频率变大,在保证平台和锚索质量不变的情况下,要满足ω1=0.5ω2,需要调节平台的刚度k由5.16×106增加到3.78×107．

对式(20)通过数值分析计算得2倍初始张力下的锚索、平台振动的位移时程曲线，如图10.

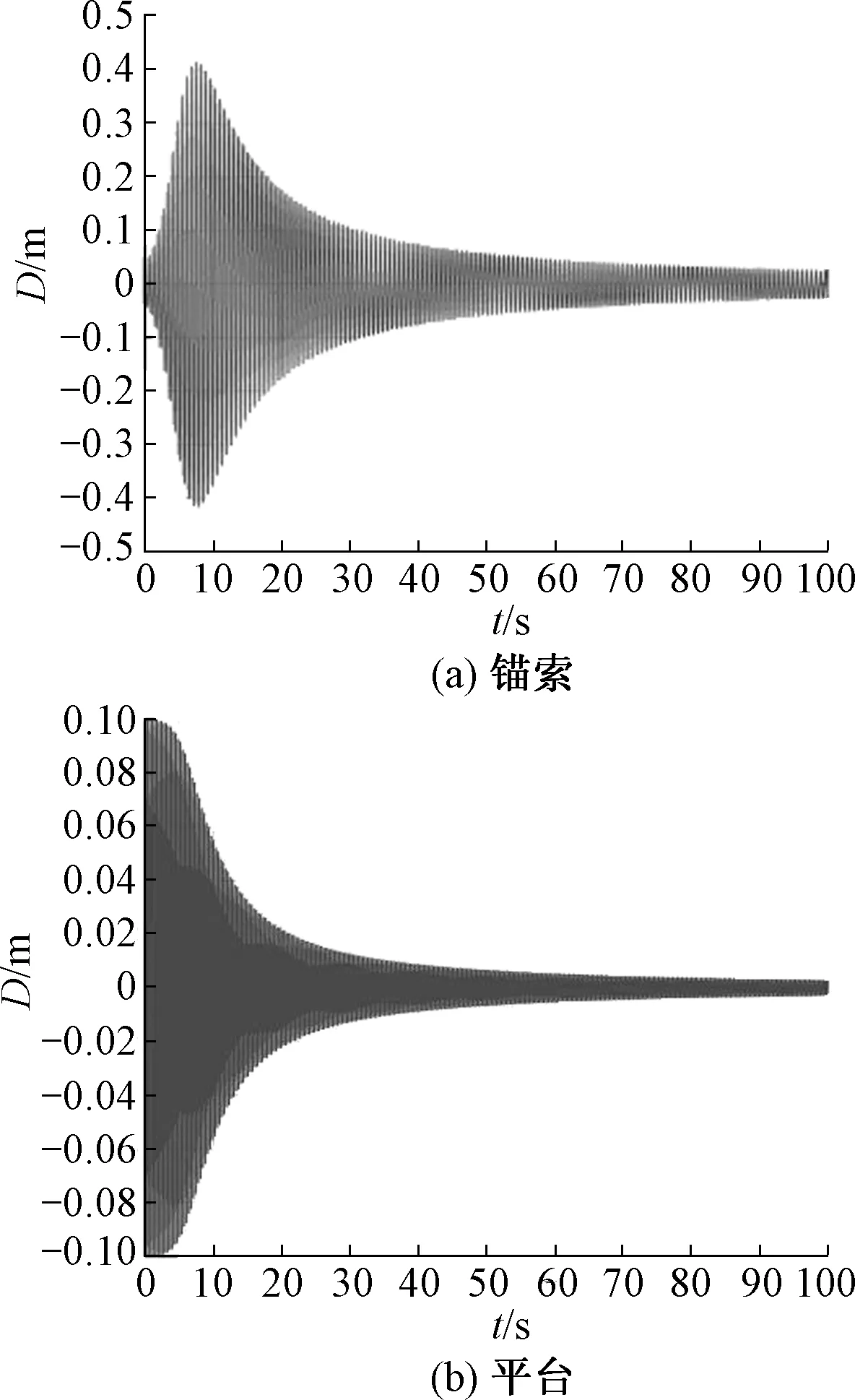
图10 工况6下锚索与平台位移时程曲线Fig.10 Displacement history of cable and platform in working condition 6

从图10(a)中的锚索位移时程曲线中可以明显看出锚索的振幅明显减小,由图7(a)中的0.6 m减小到0.42 m．同时,“拍”的现象不甚明显,锚索的振动在由0.001 m增大到0.42 m后一直持续减小至消失．但是锚索振幅的减小速度并没有发生太大的变化,均在30 s后减小到0.1 m以下;同样,图10(b)中平台的振幅亦迅速减小直至消失．不同于锚索,平台的振幅减小速度与图7(b)所示有所差异．如图10(b)，平台振幅减小有所推迟,在约20 s时图7(b)所示锚索振幅已减小到0.013 m而图10(b)所示仅减小到0.022 m,这可以理解为平台的刚度增加引起的．

2.6 阻尼对系统响应的影响

图11、12分别为工况7、8下锚索和平台的位移时程曲线．

阻尼对于振动系统有非常重要的影响．在锚索—平台耦合振动系统中除了上文讨论过的水阻尼力,系统本身还存在着阻尼．在此,假定两种不同阻尼比[15]工况7、8,分析阻尼对系统的影响．

对式(20)通过数值分析计算得两种阻尼比下的锚索和平台的位移时程曲线如图11、12.

图11 工况7下锚索与平台位移时程曲线Fig.11 Displacement history of cable and platform in working condition 7

图11(a),图12(a)分别为锚索阻尼比为0.01和平台阻尼比为0.01下锚索的位移时程曲线．从图11(a)中可以看出：相比于图7(a),锚索的最大振幅由0.62 m减小到0.57 m,减小了0.05 m;而平台的振动几乎没有改变,如图11(b)；相比于图7(a),图12(a)中锚索的最大振幅由0.62 m减小到0.27 m,减小了0.35 m;平台的振幅由0.1 m迅速减小并且在第2个“拍”内仅为0.005 m，如图12(b)．由此,在相同阻尼比条件下,增大平台阻尼对减小振幅更明显．

3 参数振动控制

锚索的参数振动主要由端部轴向激励引起的间接振动,控制端部平台的振动可以有效减小锚索的参数振动．通过在平台上加装调频质块阻尼器，如图3(d)，抑制平台的振动进而抑制锚索的参数振动．建立锚索—平台耦合振动方程组为:

(29)

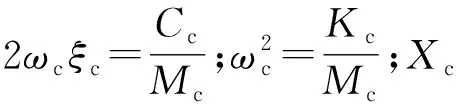
选取合适质量及刚度使得ωc≈ω2,由此抑制平台的振动．取Mc为1 000 kg,Kc为1.65×105N/m,ξc为0.01．通过数值分析计算得加装调频质块阻尼器后锚索、平台的位移时程曲线如图13.

从图13(a)中可以看出：锚索的振幅显著减小,幅值由图7(a)的0.6 m减小到0.07 m并在15 s减小到0.02 m以下．同样,从图13(b)中可以看出,平台的振动也得到了迅速的削弱,在22 s后减小到0.02 m以下．在阻尼作用下,锚索的振动能够得到迅速削弱;但在第1个“拍”内锚索瞬时参数共振的现象依然明显,如图8．相比之下,在平台加装调频质块阻尼器后,锚索的最大振幅仅为0.07 m,振幅减小较为显著．由此表明该方法对于锚索参数振动的控制是有效的．

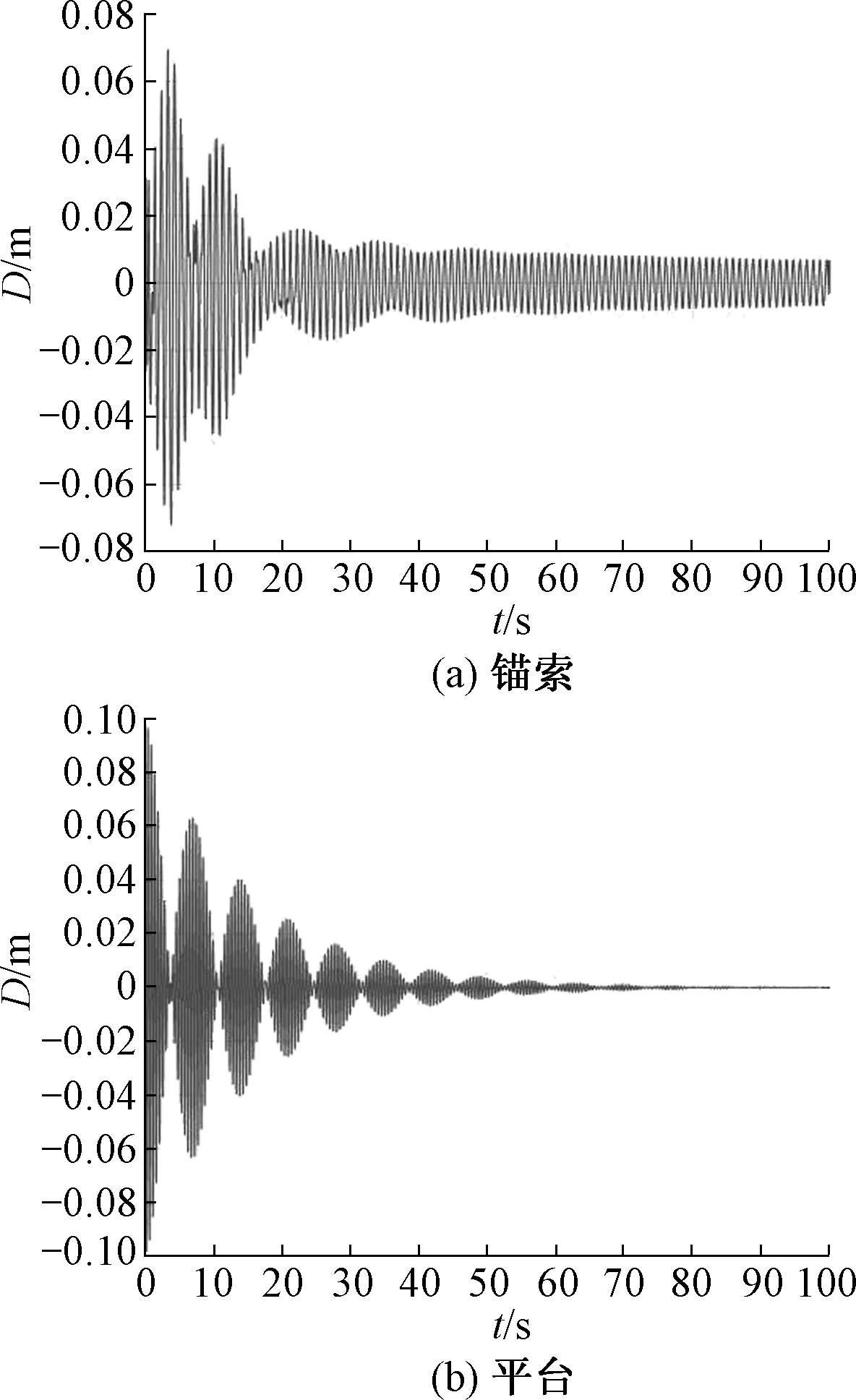
图13 加装调频质块阻尼器下锚索位移时程曲线Fig.13 Displacement history of cable and platform with Tuned Mass Damper

4 结论

通过对悬浮式F-VIVACE潮流能发电装置耦合参数振动模型的动力分析,基于牛顿法建立了考虑锚索的垂度的耦合振动方程组．其后,通过MATLAB对其进行数值计算分析,得到如下结论:

(1) 在水体的作用下锚索振动有所削弱,但瞬时的参数振动现象依然较为明显,特别是第1个“拍”内依然产生了较大的振幅．

(2) 锚索和平台初始扰动的大小均会对锚索振动产生影响;平台的初始扰动对于锚索振动的影响更为显著,即锚索的振动对平台的初始扰动更为敏感．

(3) 初始张力和阻尼均会对锚索振动产生影响;增大初始张力能够削弱锚索的振动,锚索和平台的阻尼均能减小锚索振动,但增大平台阻尼的效果更明显．

(4) 数值计算表明,在平台上安装调频质块阻尼器来控制锚索的振动效果非常显著．