基于菌群优化算法的非线性系统预测控制器设计

徐志成,陶国正,王树青

(1.常州机电职业技术学院 电气工程学院,常州 213164) (2.浙江大学工业控制技术国家重点实验室 先进控制研究所,杭州 310027)

生产实际过程中非线性系统的数学模型通常难以预测,在不需要精确的非线性系统数学模型情况下，预测控制研究显得很有必要[1-3]．对于非线性系统的预测控制,采用线性化模型或分层递阶优化方法将非线性问题转化为线性问题是目前常用的一种方式[4-5],该处理对弱非线性系统是合适的,但对一些强非线性过程,如姿态控制、化学过程控制等,并不总能获得满意效果,尤其当工作在操作点附近大范围内以及操作点摄动时,甚至连稳定性也难以保证．文献[6-7]中直接用Hammerstein模型、Volterra模型等模型作为预测模型,它们能描述许多化工设备或过程的非线性特性,如蒸馏塔、热交换器等,并且模型结构简单,方便数学处理,但只适用于工业环境中的一些特定过程[4,8-9]．

支持向量机(support vector machine,SVM)方法建立在统计学习理论基础上,其利用结构风险最小原理和VC维理论解决了优化问题中的非线性、小样本、局部极小等问题[9-11]．利用SVM方法的优点构建最小二乘支持向量机(least square-support vector machine, LS-SVM),作为非线性系统建模的有力工具,可以以任意精度逼近非线性系统[12-13]．

菌群优化(bacterial swarm foraging for optimization,BSFO)[14-15]算法作为一种新型优化方法,可进行多变量随机迭代问题求解,种群内每个细菌个体的状态表示待优化问题的一个解,个体根据自身位置和其他细菌传递过来的信息不断更新其自身状态,产生新解,从而通过个体间的协作和竞争实现全局搜索,可用来快速有效地解决预测控制器设计中目标函数的优化问题[15]．

预测模型的精确度是预测控制的关键,由于非线性系统的预测模型是非线性的,求解控制量的优化问题是非线性约束优化问题, 当控制量序列很长时,优化问题变得复杂,且可能耗费较长时间,不能满足系统实时性要求,优化结果也不一定最优,因此在每个采样时刻优化求解的控制量序列应该尽可能短[16]．针对这一问题,文中提出了一种基于BSFO算法和模型学习的单步预测控制算法,算法通过LS-SVM方法建立系统数学模型,在每个采样时刻预测下个时刻的输出,获得系统输出估计值,通过反馈校正误差,得到控制量和偏差的优化目标,利用BSFO算法具有全局性、快速性、较高精度和较低资源占用等特点,进行在线实时滚动优化，得到控制量．通过对单变量和多变量非线性系统的仿真结果表明算法具有良好的鲁棒性和自适应性．

1 BSFO算法原理[14-15,17-20]

文献[14]中提出一种智能仿生优化算法[14],与其他进化算法类似,也采用群体和进化的概念,算法包括趋药性行为、聚集行为、繁殖行为和消散行为等步骤[15，17]．

1.1 趋药性行为

趋药性行为包括前进和翻转两部分．前进是按照前一步的方向做动作,翻转是按照某一新方向前进．翻转一次后的位置为:

θi(j+1,k,l)=θi(j,k,l)+C(i)φ(j)

(1)

式中：θi(j,k,l)为第i个菌体在第j个趋化步、第k个繁殖步、第l个消散步后的更新位置；φ(j)为单位长度的随机向量；C(i)>0为行为步长．细菌在同一方向前进的最大限制步数为Ns,细菌在一个趋药性循环中的趋药性行为步数为Nc．

1.2 聚集行为

聚集行为用下式表示:

(2)

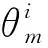
聚集行为后的适应度函数为:

J(i,j+1,k,l)=J(i,j,k,l)+JCC(θ)

(3)

1.3 繁殖行为

繁殖行为就是健康的细菌继续繁殖,不够健康的被淘汰．对于给定的k、l、i=1,2,…,S，定义

(4)

为细菌i的健康度函数,将细菌按健康度函数值由大到小排列,值越大意味着细菌越不健康,排列靠前的，健康度函数值较大的一半细菌被淘汰,健康度函数值较小的，后面一半细菌进行繁殖,每个繁殖得到子代,生成的子代与父代具有同样的生理特征,子代与父代组成新的种群,算法通过此行为确保整个群体规模不发生改变,并且保留了适应能力强的细菌．

1.4 消散行为

实际中,部分菌体由于外力的作用而消失,或者转移到其他区域中,细菌的趋药性行为被破坏,但有可能因此使细菌找到食物更好的区域,因此算法中设置了此步.从某种角度看，此步行为也属于觅食行为的一种,其帮助算法脱离局部最优值,寻找全局最优值．菌群经过繁殖行为后,以某一概率被随机分布到寻优区间,算法实施中假设此概率为ped．

2 基于BSFO算法的LS-SVM预测控制

2.1 LS-SVM非线性预测模型

对一个带约束,输入和输出分别为m和n维的离散多变量非线性系统:

(5)

u(k)=(u1(k),u2(k),…,um(k))∈Rm为k时刻输入；y(k)=(y1(k),y2(k),…,yn(k))∈Rn为k时刻输出；d为输出延迟；q为输入阶次；p为输出阶次；控制量的取值范围和变化幅度通过约束条件限定．

对于

(6)

将样本从原空间映射到特征空间通过非线性映射φ实现,特征空间中的LS-SVM估计模型为:

f(x)=ωTφ(x)+b

(7)

式中：ω为权重系数；b为偏置.系统优化目标是使函数:

(8)

函数的最优估计使目标函数式(9)最小化:

(9)

利用下面的Lagrange函数对上式进行求解．

(10)

αk(k=1,…,N)为Lagrange乘子．

根据KKT条件和Mercer条件[21],令Lagrange函数偏导等于0,有:

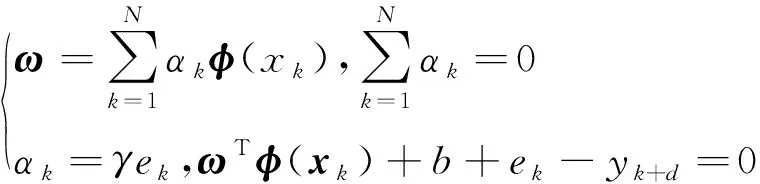
(11)

得到LS-SVM预测模型为:

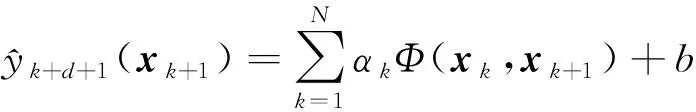
(12)

式中，Φ(xi,xj)=φT(xi)φ(xj)为定义的核函数．

2.2 预测控制器设计

预测控制器框图如图1．

图1 预测控制器框图Fig.1 Block diagram of predictive controller

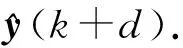
(13)

则修正输出:

(14)

对m维输入、n维输出的非线性系统设计预测控制器,定义式(15)为控制量对应的适应值函数,BSFO算法就是要获得式(15)的最小值．

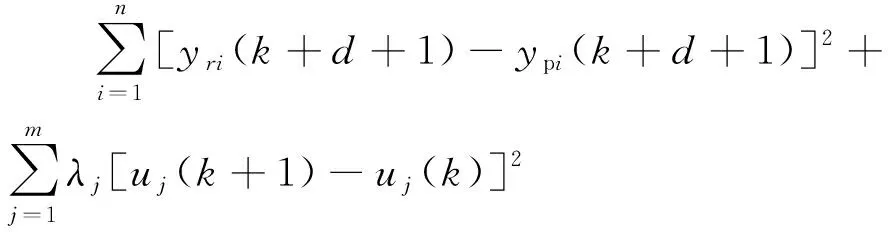
(15)

2.3 算法步骤

(1) 对系统状态、LS-SVM及BSFO算法参数进行初始化;

(2) 使用激励信号得到输入输出数据,从而构成样本集,然后对训练样本使用LS-SVM算法获得对应的预测模型;

(3) 利用样本对模型进行测试,确保误差在允许范围内,如果不满足要求,则调整LS-SVM参数，重新训练直到满足要求;

(5) 根据BSFO算法步骤,循环优化得到最优控制量u(k+1),算法终止条件是达到最大迭代次数;

(6) 将u(k+1)作用于非线性系统．

3 仿真研究

3.1 单输入单输出系统

以非线性液位系统为研究对象[22-23],该单输入单输出系统数学模型描述为式(16)．文献[22]中设计了NN自 适 应 控 制 器,文献[23]中采用基于递归模糊NN的广义预测控制，控制效果均不错．然而,前者需要系统精确的数学模型且其瞬态增益必须为正;后者控制器复杂且计算量大．

输入为[0,1]均匀分布随机序列,输出延迟d=1,分别选取200和300组形如[ys(k),ys(k-1),us(k),us(k-1)),ys(k+1)]的样本集作为训练集和测试集．利用LS-SVM建立预测模型,正则化参数γ=1 000,高斯核函数的宽度参数σ2=10．为方便比较,使用BP神经网络建立预测模型,参数最大训练次数为3 000,允许误差为10-5,算法结果表明LS-SVM预测模型结果优于BP-NN算法(表1)．

ys(k+1)=0.972 2ys(k)+0.357 8us(k)-

0.129 5us(k-1)-0.310 3ys(k)us(k)-

0.308 4ys(k)ys(k-1)us(k-1)+

0.108 7ys(k-1)us(k)us(k-1)

s.t. -2≤us≤2

(16)表1 LS-SVM和BP-NN结果比较Table 1 Comparison results of LS-SVM and BP-NN

BSFO算法参数S=10,Ns=3,Nc=5,Nre=5,Ned=2,ped=0.25,dattract=0.1,ωattract=0.2,hrepellant=0.8,ωrepellant=10．系统初值us(1)=0.613 3,ys(1)=0.667 7,ys(2)=0.612 5．算法优化获得每个控制量的时间不超过1.2 s,算法终止条件为迭代次数达到10,系统参考轨迹为单位幅值的方波,图2为控制量输出,图3为系统输出．

图2 单输入单输出系统控制量输出Fig.2 Control variable output of SISO system

为测试控制器的自适应性和鲁棒性,参考值前80个时刻为0.2,80个时刻后变为一个频率逐渐变大的余弦信号,并且在第56个时刻变成大小为0.4的干扰信号.图4为系统输出.可以看出,系统输出虽然出现一定的扰动,但影响不大,并且能很快恢复正常．因此,通过BSFO算法优化得到的LS-SVM预测控制器能够在不改变任何参数的情况下快速跟踪新的参考轨迹,具有较好的自适应性和鲁棒性．

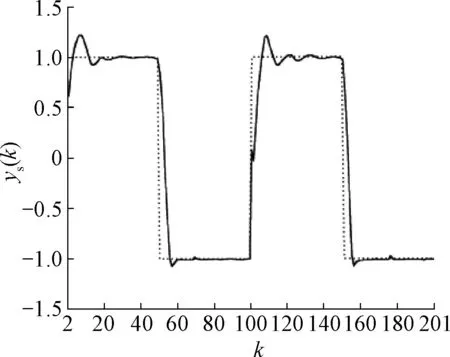
图3 单输入单输出系统输出Fig.3 Output of SISO system

图4 加干扰信号后单输入单输出系统输出Fig.4 Output of SISO system with interference signal

3.2 多输入多输出系统

选取式(17)的非线性系统作为研究对象:

(17)

输入为[0,1]均匀分布随机序列,d=2,分别选取形如[(y1(k),u1(k-1),u2(k-2)),y1(k+1)]和[(y2(k),u1(k-2),u2(k-1)),y2(k+1)]的900和200组数据作为训练样本集和测试样本集,用LS-SVM建立预测模型,参数γ=1 000,σ2=3,结果如表2．

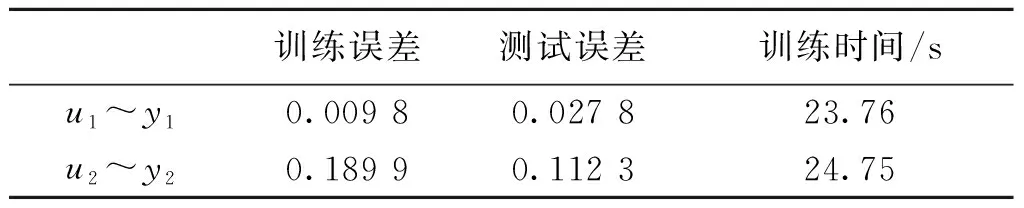
表2 LS-SVM预测模型训练和测试结果Table 2 Training and testing results of LS-SVM predictive model

u(1)=0,y(1)=y(2)=y(3)=2.5,BSFO算法参数和参考轨迹设置与单输入单输出相同,算法终止条件为迭代次数达到15,优化每个控制量的时间小于0.7 s．图5～8分别为系统对方波跟踪的效果和相应的控制量．

图5 多输入多输出系统输出y1Fig.5 Output y1 of MIMO system

图6 多输入多输出系统输出y2Fig.6 Output y2 of MIMO system

图7 多输入多输出系统控制量输出u1Fig.7 Control variable output u1 of MIMO system

图8 多输入多输出系统控制量输出u2Fig.8 Control variable output u2 of MIMO system

可以看出,当输入发生变化时,控制量能及时调整,系统能较好地跟踪输入变化,因此,对于MIMO系统,用文中方法设计的控制器同样适用．

综上,与文献[20]和[21]中的方法相比,文中算法不需要系统精确的数学模型,计算量较小,并且所设计的预测控制器具有较好的自适应能力和鲁棒性．

4 结论

文中将BSFO算法应用到非线性系统预测控制中,提出了一种基于BSFO算法的单步预测控制方法,利用LS-SVM方法来建立非线性系统的预测模型,通过BSFO算法在线实时滚动优化确定控制量,有效解决了非线性系统预测控制器设计问题．通过单变量和多变量非线性系统实例对算法进行了仿真研究,结果表明了算法具有较好的自适应能力和鲁棒性．